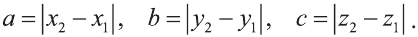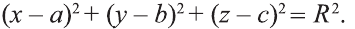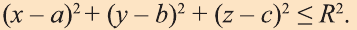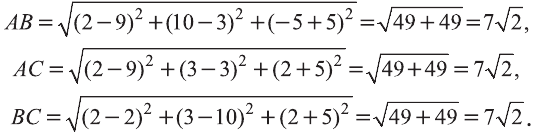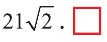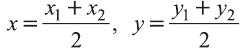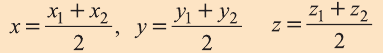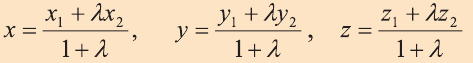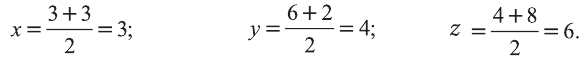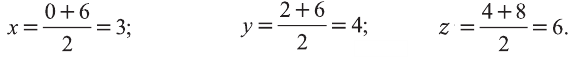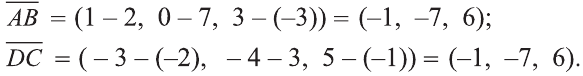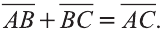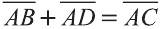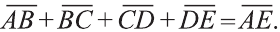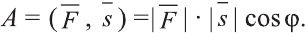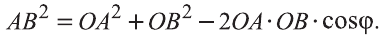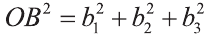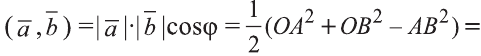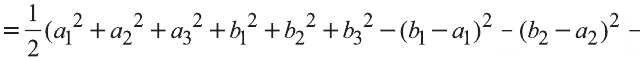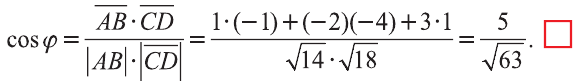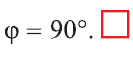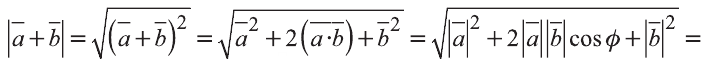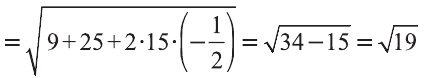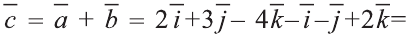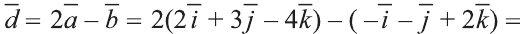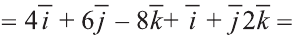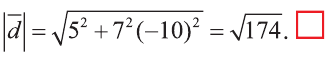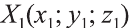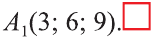Координаты прямоугольного треугольника в пространстве

Содержание:

Видео:Как построить точки в системе координат OXYZСкачать

Система координат в пространстве

Декартова система координат в пространстве

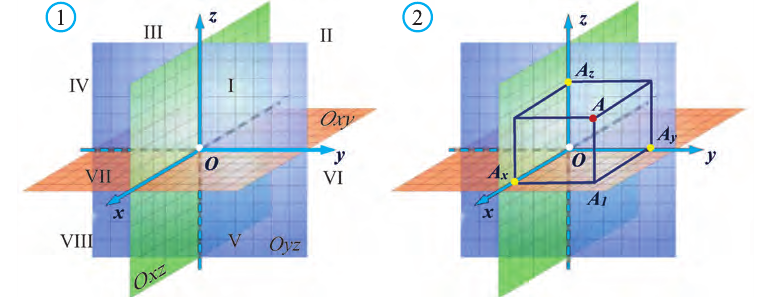
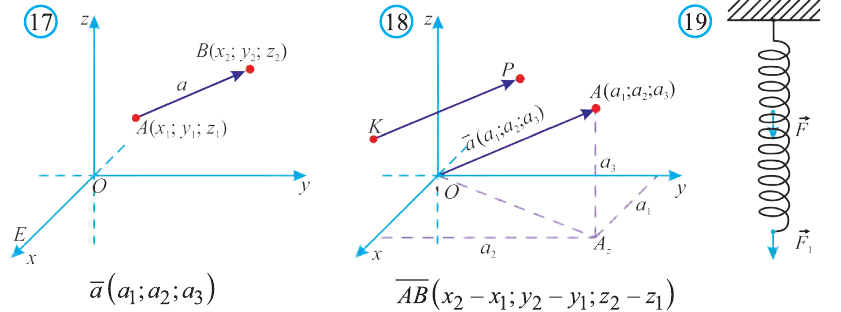
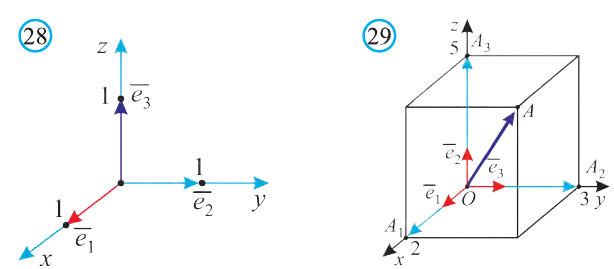
Вы познакомились с декартовой системой координат на плоскости в предыдущих классах. Систему координат в пространстве введём аналогично тому, как это было сделано на плоскости. Рассмотрим три взаимно перпендикулярных оси Ох, Оу и Оz, пересекающихся в точке О, являющейся началом координат. Через каждую пару этих прямых проведём плоскости Оху, 0xz и Оуz (рис. 1). Таким образом вводится система координат в пространстве, при этом

точку О — называют началом координат, прямые Ох, Оу и Оz — осями координат, Ох — ось абсцисс, Оу — ось ординат и Оz — ось аппликат, плоскости Оху, Оуz и Охz — координатными плоскостями.

Координатные плоскости делят пространство на 8 октант (получетвертей) (рис. 1).

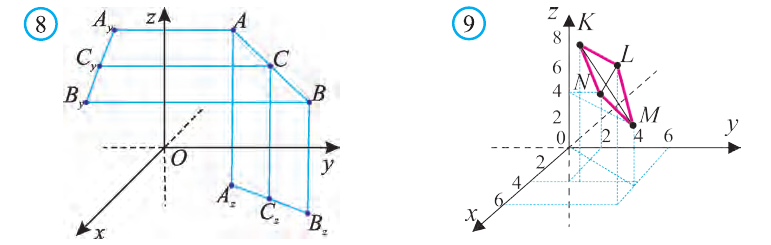
Пусть в пространстве задана произвольная точка А. Через эту точку проведём плоскости, перпендикулярные плоскостям Охz, Оуz и Охz (рис. 2). Одна из этих плоскостей пересечёт ось Ох в точке Ах.

Координату Ах на оси Ох называют координатой х или абсциссой точки А.

Аналогично определяют у — координату (ординату) и z- координату (аппликату) точки А.

Координаты точки А записывают в виде А (х; у; z) или короче (х; у; z). Точки, изображённые на рисунке 3, имеют следующие координаты: А (0; 5; 0), B (4; 0; 0), М (0; 5; 4), К (2; 3; 4), Р (-2; 3; -4).

Пример:

Пусть в пространстве в декартовой системе координат

задана точка А (2; 3; 4). Где она расположена?

Решение:

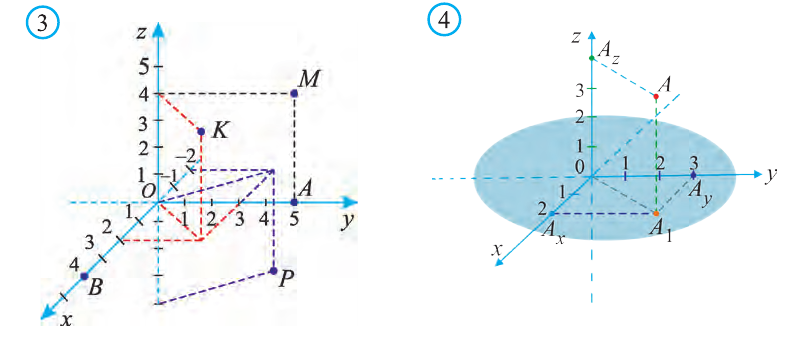
От начала координат в положительном направлении осей Ох и Оу отложим отрезки ОА_х = 2 и ОА_у = 3 (рис. 4).

Через точку А_х проведём прямую, лежащую в плоскости Оху и параллельную оси Оу. А через точку Аy проведём прямую, лежащую в плоскости Оху и параллельную оси Ох. Точку пересечения этих прямых обозначим A₁ . Через точку A₁ проведём прямую, перпендикулярную плоскости Оху и на ней в положительном направлении Oz отложим отрезок АА₁ = 4. Тогда точка А (2; 3; 4) и будет искомой точкой.

Пользуясь системой координат, созданной для современных программируемых станков и автоматизированных роботов, составляются программы, на основе которых обрабатываются металлы (рис. 5).

Расстояние между двумя точками

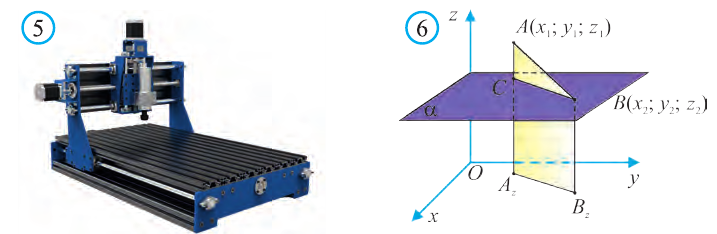
1.Сначала рассмотрим случай, когда прямая АВ не параллельна оси Оz (рис. 6). Через точки А и В проведём прямые, параллельные оси Оz. И пусть они пересекают плоскость Оху в точках А_z и В_z .

Координаты х и у этих точек соответственно равны координатам х и у точек А, В, а координаты z равны 0.

Теперь через точку В проведём плоскость а, параллельную плоскости Оху. Она пересечёт прямую АА_z в некоторой точке С.

По теореме Пифагора: АВ 2 = АС 2 + СВ 2 .

Однако

Поэтому

2.Пусть отрезок АВ параллелен оси Оz, тогда 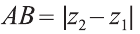и, так как

Следовательно, расстояние между двумя точками А и В:

(1)

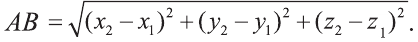
Примечание. Формула (1) выражает длину диагонали прямоугольного параллелепипеда, измерения которого равны

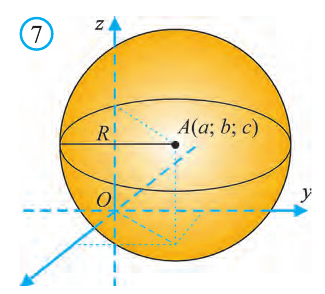
Уравнение сферы и шара

Известно, что множество всех точек М (х; у; z), расположенных на расстоянии R от данной точки А (а; Ь; с) образуют сферу (рис. 7). Тогда по формуле (1) координаты всех точек, расположенных на сфере радиуса R с центром в точке А (а; b; с), удовлетворяют равенству

Отсюда, ясно, что неравенство для точек шара радиуса R с центром в

точке А (а; b; с) имеет вид:

Пример:

Найдите периметр треугольника ABC с вершинами в

Решение:

Р=АВ+АС+ВС периметр треугольника ABC. Воспользовавшись формулой 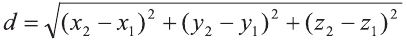расстояния между двумя точками, найдём длины сторон треугольника:

Следовательно, треугольник ABC равносторонний и его периметр .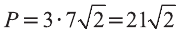

Ответ:

Координаты середины отрезка

Пусть А (x₁; y₁;z₁) и В (х₂; у₂; z₂) — произвольные точки, точка С (х; у; z) середина отрезка AB (рис. 8).

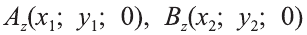
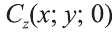
Через точки А, В и С проведём прямые, параллельные оси пересекающие плоскость Оху в точках и . Тогда по теореме Фалеса точка С_z — середина отрезка А_zВ_z.

Отсюда по формулам нахождения координат середины отрезка на плоскости

Чтобы найти координату z, нужно вместо плоскости Оху рассмотреть плоскость 0xz или Оуz.

Тогда и для z получим формулу, подобную вышеприведённой.

Аналогично, используя координаты концов A и B отрезка AB, по формулам

находят координаты точки Р(х1;у]; г,), делящей отрезок АВ в отношении X САР: РВ = X).

Доказательство: Для решения задачи используем признак параллелограмма: Четырёхугольник, точка пересечения диагоналей которого делит их пополам, является параллелограммом.

Координаты середины отрезка МК:

Координаты середины отрезка NL:

Координаты середин отрезков МК и NL равны. Это говорит о том, что отрезки пeрeсeкаются и в точке пeрeсeчeния делятся пополам. Следовательно, четырёхугольник MNLK — параллелограмм.

В переписке с известным целителем и математиком Абу Али ибн Сино Абу Райхон Беруни задаёт следующий вопрос: «Почему Аристотель и другие (философы) называют шесть сторон?»

Рассматривая шестисторонний куб, Беруни говорит о фигурах «с другим количеством сторон» и добавляет, что «шарообразные фигуры не имеют сторон.» А Ибн Сино отвечает, что «во всех случаях нужно считать, что сторон шесть, так как у каждой фигуры, независимо от её формы, есть три измерения — длина, глубина и ширина».

Здесь Ибн Сино имеет ввиду три координаты, именуемые условно «шесть сторон».

В произведении «Канон Масъуда» Беруни приводит точное математическое определение шести сторон: «Сторон шесть, так как они ограничивают движение фигур по своим измерениям. Измерений три: длина, ширина и глубина. А их в два раза больше самих измерений.»

В предыдущих книгах автор определяет положение небесных тел с помощью двух координат относительно небесной сферы — эклиптического уравнения. Либо через те же координаты, но относительно небесного экватора или горизонта. Однако при определении взаимного расположения звёзд и небесных светил придётся учитывать и случаи затмений. Вот в таких случаях появляется необходимость в третьей сферической координате. Эта необходимость привела Беруни к отказу от теории небесных координат.

Векторы в пространстве и действия над ними

Векторы в пространстве

Понятие вектора в пространстве вводят также как на плоскости.

Вектором в пространстве называют направленный отрезок. Основные понятия, относящиеся к векторам в пространстве, аналогичны этим понятиям на плоскости: длина (модуль), направление вектора, равенство векторов.

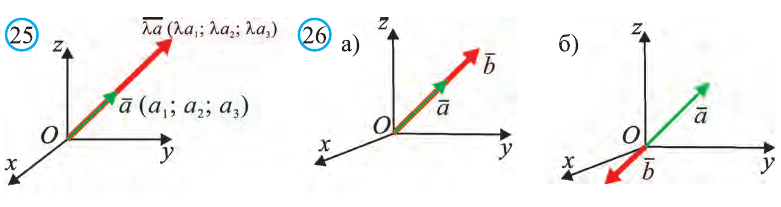
Координатами вектора с началом в точке А (х₁; у₁; z₁) и концом в точке В (х₁; у₁; z₁) называют числа 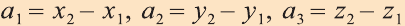, (рис. 17).

Приведем без доказательства свойства векторов, аналогичных свойствам на плоскости.

Также как на плоскости, соответствующие координаты равных векторов равны и, обратно, векторы с равными координатами равны.

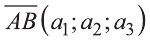
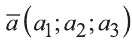
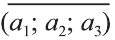
Hа основании этого вектор можно обозначить как или или кратко (рис. 18).

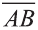
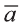
Вектор можно записать и без координат (или ). В этой записи

на первом месте начало вектора, а на втором — конец.

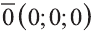
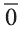
Вектор с координатами, равными нулю, называют нулевым вектором и обозначают или , направление этого вектора не определено.

Если начало вектора расположено в начале координат О, а числа а₁,

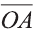
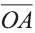
координатами вектора : (а₁; а₂; а₃).

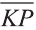
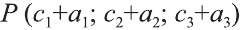
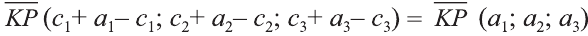
Однако вектор в пространстве с началом в точке К(с₁; с₂; с₃) и концом в точке будет иметь те же координаты: .

Отсюда следует, что вектор можно приложить к любой точке пространства. В геометрии мы рассматриваем такие свободные векторы. Но в физике, обычно вектор связан с некоторой точкой. Например, воздействие силы приложенная к пружине F на рисунке 19 зависит от точки её приложения.

Длинной вектора называют длину направленного отрезка

изображающего его (рис. 17). Длину вектора записывают

так. Длина вектора , заданного координатами,

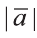
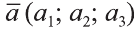
вычисляется по формуле .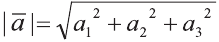

Пример:

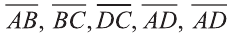
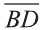
Даны точки А (2; 7;-3),В (1; 0; 3), С (-3;-4; 5) и D (-2; 3; -1). Какие из векторов и равны между собой?

Решение:

У равных векторов равны соответствующие координаты. Поэтому найдём координаты векторов:

Следовательно, .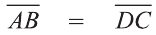

Докажите самостоятельно, что

Действия над векторами в пространстве

Действия над векторами. Сложение векторов, умножение на число и их скалярное произведение определяется также как на плоскости.

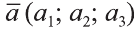
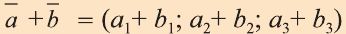
Суммой векторов и (b₁; b₂; b₃); называют вектор (рис. 20).

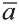
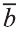
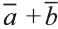
Пусть кран на рисунке 20.b движется вдоль вектора , а груз относительно крана вдоль вектора . В результате груз движется вдоль вектора . Поэтому из рисунка 20.с, на котором изображён сюжeт басни русского писателя И.А.Крылова, ясно, что герои басни не смогут сдвинуть телегу с места.

Свойства суммы векторов

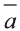
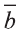
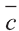
Для любых векторов , и имеют место следующие свойства:

a) — переместительный закон сложения векторов;

b) — распределительный закон сложения.

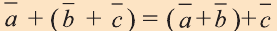
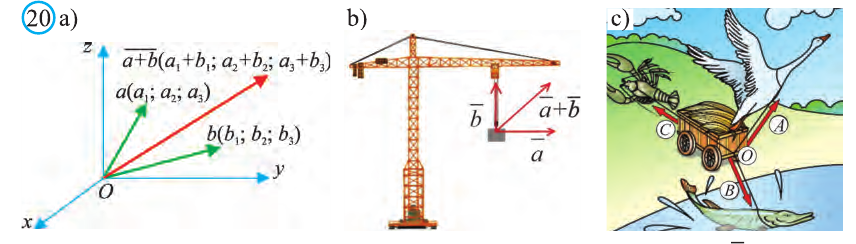
Правило треугольника сложения векторов

Для любых точек А, В и С (рис. 21):

Правило параллелограмма сложения векторов

Если АВСD — параллелограмм (рис. 22), то

Правило многоугольника сложения векторов

Если точки А, В, С, D и Е — вершины многоугольника (рис. 23), то

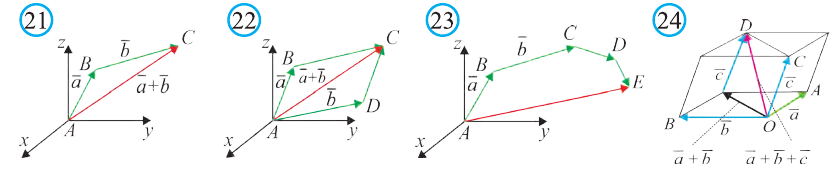
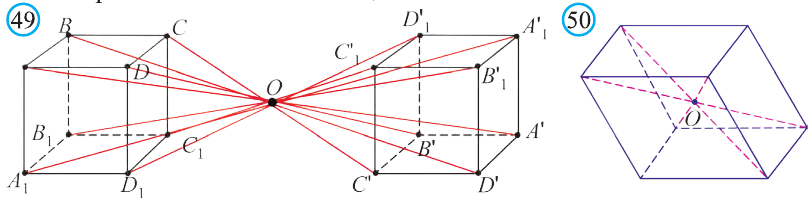
Правило параллелепипеда сложения трёх векторов, не лежащих в одной плоскости. Если АВСDА₁В₁С₁D₁ параллелепипед (рис. 24), то

.

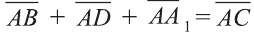
Вектор ​​​​​​= (a1; a₂; a₃) — называют умножением вектора

(a₁; a₂; a₃) на число (рис. 25). Свойства операции умножения вектора на число.

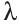
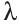
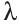
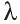
Для любых векторов и и чисел и

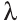
а);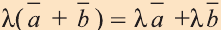

b);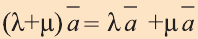

c) 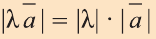и направление вектора

совпадает с направлением вектора , если ,

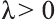
противоположно направлению вектора , если .

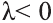
Коллинеарные и компланарные векторы

Пусть заданы ненулевые векторы и . Если векторы

и сонаправлены или противоположно направлены,

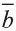
то их называют коллинеарными векторами (рис. 26).

Свойство 1. Если для векторов и имеет место равенство , то они коллинеарны и наоборот.

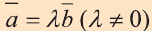
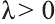
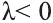
Если , то векторы и сонаправлены , если, то

противоположно направлены .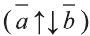

Свойство 2. Если векторы (a₁; a₂; a₃) и (b₁; b₂; b₃) коллинеарны,

то их соответствующие координаты пропорциональны:

и наоборот.

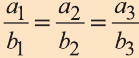
Пример:

Найдите вектор с началом в точке А (1; 1; 1) и концом в точке В, лежащей в плоскости Оху, коллинеарный вектору ( 1; 2; 3).

Решение:

Пусть точка В имеет координаты В (х; у; z). Так как точка В лежит в плоскости Оху, то z=0. Тогда 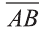(х — 1 ;у — 1; — 1).

По условию задачи векторы 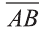(х — 1 ;у — 1; — 1) и (1, 2, 3) коллинеарны. Следовательно, их координаты пропорциональны.

Тогда получаем следующие пропорции .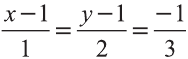

Откуда находим , .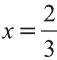

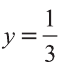
Итак,

Векторы, лежащие в одной плоскости или параллельных плоскостях, называют компланарными векторами (рис. 27).

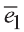
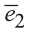
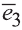
Векторы (1; 0; 0), (0; 1; 0) и (0; 0; 1) называют ортами (рис. 28).

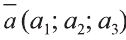
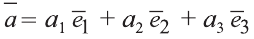
Любой вектор можно единственным образом разложить по ортам, то есть представить в виде (рис. 29).

Точно также, если заданы три нeкомпланарных вектора и , то любой вектор можно единственным образом представить в виде:

.

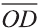
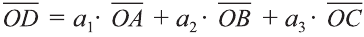
Здесь 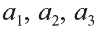некоторые действительные числа. Тогда говорят, что вектор разложен по заданным векторам.

Скалярное произведение векторов

Углом между ненулевыми векторами и называют угол между направленными отрезками векторов = и =, исходящих из точки О (рис. 30).

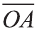
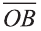
Угол между векторами и обозначают так .

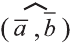
Скалярным произведением векторов и называют произведение длин этих векторов на косинус угла между ними.

Если один из векторов нулевой, то скалярное произведение этих векторов равно нулю.

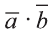
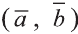
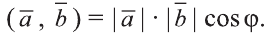
Скалярное произведение обозначают или . По определению (1)

Из определения следует, что если скалярное произведение векторов и равно нулю, то эти векторы перпендикулярны и наоборот.

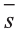
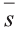
В физике работа A, выполненная при движении тела на расстоянии , под воздействием силы (рис. 31), равна скалярному произведению силы на расстояние:

Свойство. Если 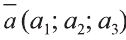и (b₁; b₂; b₃), то () =

Доказательство. Приложим векторы 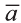и к началу

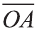
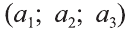
координат О (рис.32). Тогда = и = (b₁; b₂; b₃).

Если векторы неколлинеарны, то получаем треугольник АВО , для которого справедлива теорема косинусов.

Тогда .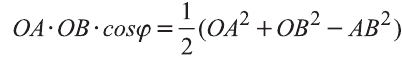

Однако, ,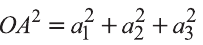

и .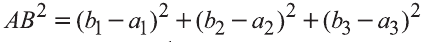

Следовательно,

.

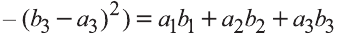
Самостоятельно докажите, что и в случае, когда данные векторы коллинеарны 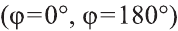, также выполняется

это равенство.

Свойства скалярного произведения векторов

1. — переместительное свойство.

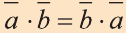
2. — распределительное свойство.

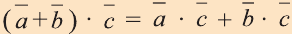
3. — сочетательное свойство.

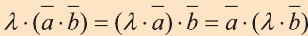
4.Если векторы а и b являются сонаправленными коллинеарными

векторами, то 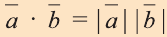, так как соs 0° = 1.

5.Если же векторы противоположно направлены, то 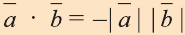, так как cos l80° = -1.

6. .

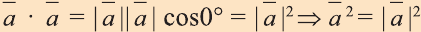
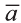
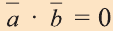
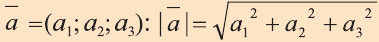
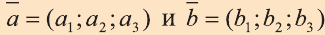
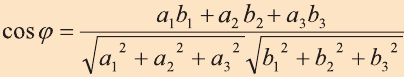
7. Если вектор перпендикулярен вектору , то . Следствия: а) Длина вектора ; (1) b) косинус угла между векторами

: ; (2)

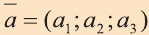
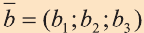
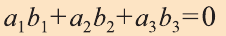
с) условие перпендикулярности векторов и

.

(3)

Пример:

— заданные точки. Найдите косинус угла между векторами .

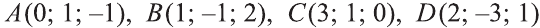
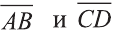
Решение:

Найдём длины векторов :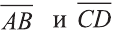

,

.

,

.

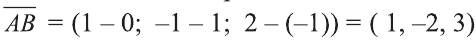
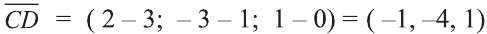
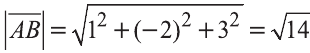
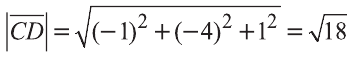
Пример:

Найдите угол между векторами .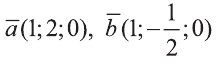

Решение:

Итак,

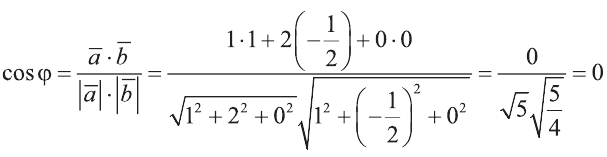
Пример:

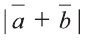
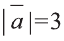
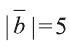
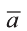
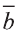
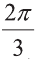
Найдите , если , и угол между векторамии равен .

Решение:

Пример:

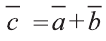
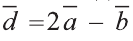
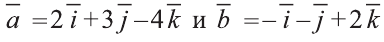
Найдите координаты и длины векторов 1); 2), если .

Решение:

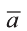
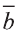
Подставим в выражения искомых векторов разложения векторов и по координатам:

1)

. Следовательно,.

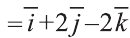
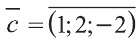
Тогда.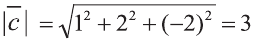

2)

.

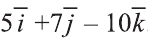
Следовательно, .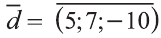

Тогда

Пример:

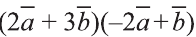
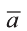
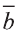
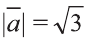
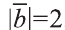
Найдите произведение, если угол между векторами и равен 30° и , .

Решение:

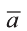
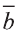
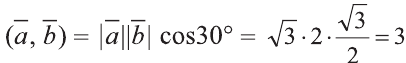
Сначала найдём поизведение векторов и :

.

Затем перемножим заданные выражения как многочлены

и, пользуясь распределительным свойством умножения

вектора на число, получим:

.

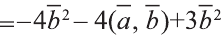
Учитывая, что ,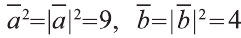

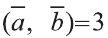
найдём искомое произведение

Преобразование и подобие в пространстве

Геометрические преобразования в пространстве

Если каждую точку заданной в пространстве фигуры F изменить одним и тем же способом, то получим фигуру F_1. Если при этом преобразовании различные точки первой фигуры переходят в различные точки второй, то говорят о преобразовании геометрической фигуры.

Если рассматривать все пространства как геометрическую фигуру, то также можно говорить о преобразовании геометрической фигуры.

Понятие геометрического преобразование в пространстве вводят также как на плоскости. Следовательно, свойства некоторых рассматриваeмых ниже видов преобразований и их доказательства также подобны соответствующим им на плоскости. Поэтому, мы не будем доказывать их и рекомендуем провести их самостоятельно.

Движение и параллельный перенос

Преобразование фигур, при котором сохраняются расстояния между точками, называют движением. Можно привести следующие свойства движения. При движении прямая переходит в прямую, луч — в луч, отрезок — в равный ему отрезок, угол — в равный ему угол, треугольник — в равный ему треугольник, плоскость — в плоскость, тетраэдр — в равный ему тетраэдр.

В пространстве фигуры, которые можно перевести одну в другую при некотором движении называют равными фигурами.

Простейшим примером движения является параллельный перенос.

Пусть в пространстве даны вектор 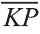и произвольная точка Х

(рис. 44). Говорят, что точка Х перешла в точку X₁ параллельным

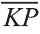
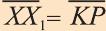
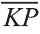
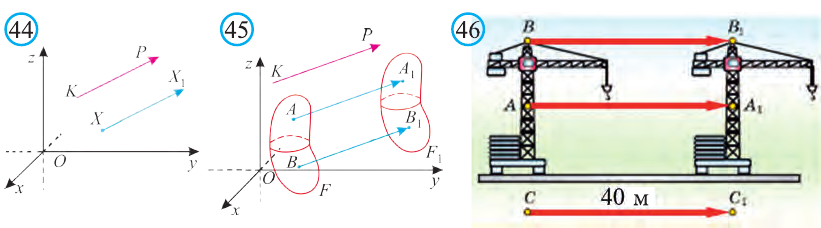
переносом на вектор , если выполняется условие . Если каждую точку фигуры F сдвинуть на вектор при помощи параллельного переноса (рис. 45), то получим фигуру F₁. Тогда говорят, что фигура F получена параллельным переносом фигуры F₁ . При параллельном переносе каждая точка фигуры F сдвигается в одном и том же направлении на одно и то же расстояние.

Каждая точка подъёмного крана, изображённого на рисунке 46, параллельно перенесена на 40 м относительно начального положения.

Ясно, что параллельный перенос является движением. Поэтому прямая переходит в прямую, луч — в луч, плоскость — в плоскость,

Пусть точка 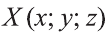фигуры F перешла в точку

фигуры F₁ при помощи параллельного переноса

на вектор .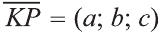

Тогда по определению получим:

или

.

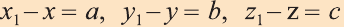
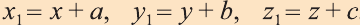
Эти равенства называют формулами параллельного переноса.

Пример:

В какую точку перейдёт точка Р (-2; 4; 6) при параллельном переносе на вектор 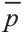= (3; 2; 5)?

Решение:

По вышеприведённым формулам параллельного переноса: .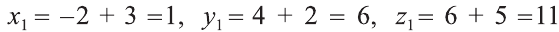

Ответ: .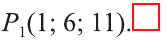

Центральная симметрия в пространстве

Если в пространстве 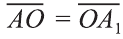, то есть точка О — середина отрезка АА₁ то точки А и А₁ называют симметричными относительно точки О.

Если в пространстве каждая точка фигуры F переходит в точку, симметричную относительно точки О (рис. 47), то такое преобразование называют симметрией относительно точки О. На рисунках 48, 49 изображёны фигуры симметричные относительно точки О. Симметрия относительно точки является движением.

Если при симметрии относительно точки О фигура F переходит в себя, то её называют центрально симметричной фигурой.

Например, диагонали параллелепипеда (рис. 50) относительно их точки пересечения О являются центрально симметричными фигурами.

Пример:

В какую точку перейдет точка A = (1; 2; 3) при симметрии относительно точки О (2; 4; 6)?

Решение:

Пусть А₁ = (х; у; z) — искомая точка. По определению точка

О — середина отрезка АА₁. Следовательно,

Из этих уравнений получаем:

.

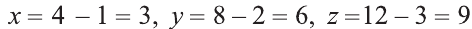
Ответ:

Симметрия относительно плоскости

Точки А и А₁ называют симметричными относительно плоскости а,

если плоскость перпендикулярна отрезку и делит его пополам (рис. 51). Фигуры F₁, и F₂ на рисунке 52 симметричны относительно

плоскости а. Очевидно, что наш силуэт и его отражение симметричны относительно плоскости зеркала (рис. 53).

Симметрия относительно плоскости а является движением.

Поэтому при симметрии относительно плоскости а отрезок переходит в равный ему отрезок, прямая — в прямую, плоскость — в плоскость.

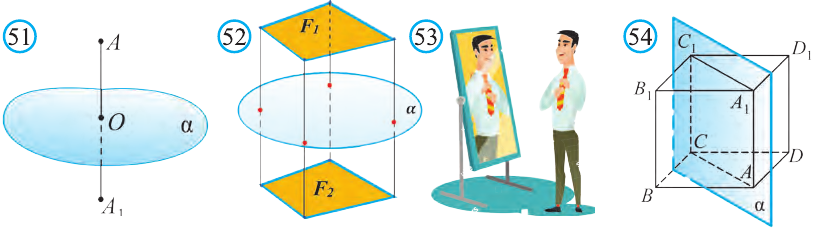
Если при симмeтрии относительно плоскости фигура F переходит в себя, то её называют фигурой симметричной относительно плоскости.

Например, изображённый на рисунке 54 куб, есть фигура, симметричная относительно плоскости а, проходящей через его диагонали АА₁ и СС₁.

Поворот и симметрия относительно оси

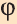
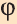
Пусть в пространстве заданы точки А и А₁ и прямая l. Если перпендикуляры АК и А₁К, опущенные на прямую l, равны и образуют угол , то говорят, что точка А перешла в точку А₁ в результате поворота на угол относительно прямой l (рис. 55).

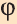
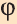
Если каждую точку фигуры F повернуть на угол относительно прямой l, то получим новую фигуру F₁ . Тогда говорят, что фигура F перешла в фигуру F₁ с помощью поворота на угол относительно прямой l. На рисунке 56 мы видим фигуры, полученные таким поворотом. Например, повернув куб, изображённый на рисунке 57, на 180° относительно прямой l, получим новый куб.

Поворот относительно прямой также является движением.

Поворот на 180° относительно прямой l называют симметрией относительно прямой l.

Центр, ось и плоскость симметрии называют элементами симметрии. Точки, симметричные точке А (х; у; z) относительно координатных плоскостей, координатных осей и начала координат, будут иметь следующие координаты:

Симметрия в природе и технике

В природе на каждом шагу можно встретить симметрию.

Например, множество живых существ, в частности тела человека и животных, листья растений и цветы устроены симметрично (рис. 58). Также в неживой природе есть элементы, например, снежинки, кристаллы соли. Молекулярное строение веществ тоже состоит из симметричных фигур. Это, конечно, неспроста, поскольку симметричные фигуры не только красивы, но и самые устойчивые.

Раз так, то можно считать, что красота и совершенство природы построены на основе симметрии. Взяв за основу природную красоту и совершенство, строители, инженеры и архитекторы создают строения и механизмы, здания и сооружения, технику и транспортные средства симметричными. В этой работе им очень помогает наука геометрия.

Подобие пространственных фигур

Пусть 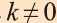и преобразование переводят фигуру F₁, в фигуру F₂. Если

при этом преобразовании для произвольных точек X₁ и Х₂ фигуры F₁ и соответствующих им точек Y₁ и Y₂ фигуры 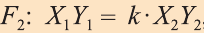, то это преобразование называют преобразованием подобия (рис. 59).

Как видим, понятие преобразования подобия в пространстве вводится также как на плоскости. Следовательно, рассматриваемые ниже виды подобия, их свойства и доказательства этих свойств подобны соответствующим на плоскости. Поэтому, мы не будем останавливаться на их доказательствах и рекомендуем провести их самостоятельно. Преобразование подобия в пространстве отображает прямую в прямую, луч в луч, отрезок в отрезок и угол в угол. Точно также это преобразование плоскость отображает в плоскость.

Если в пространстве одна из фигур перешла в другую с помощью преобразования подобия, то эти фигуры называют подобными.

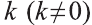
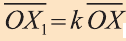
Пусть в пространстве задана фигура F, точка О и число к . Преобразование, переводящее произвольную точку X фигуры F в точку Х₁ удовлетворяющую условию , называют гомотетией относительно центра О с коэффициентом (рис. 61). Точку О называют центром гомотетии, а число коэффициентом гомотетии. Если в результате такого преобразования каждой точки фигуры F получена фигура F₁ то говорят, что фигура F гомотетична фигуре F₁.

Вы видите, что определение гомотетии в пространстве аналогично соответствующему определению на плоскости. Следовательно, все свойства и их доказательства аналогичны. Поэтому, мы не будем доказывать их и рекомендуем провести их самостоятельно.

Гомотетия относительно точки О с коэффициентом является преобразованием подобия. Гомотетия с отличным от нуля коэффициентом при = 1 отображает фигуру F в себя, а при =-1 в фигуру F₁ симметричную фигуре F относительно точки О. В остальных случаях гомотетии не сохраняет расстояния между точками, т. е. не является движением. В результате гомотетии расстояние между точками увеличивается в одно и тоже число раз, т. е. меняются измерения фигуры, но сохраняется её форма. При гомотетии а) прямая отображается в параллельную ей прямую (рис. 62.а); b) плоскость — в параллельную ей плоскость (рис. 62.b), если они не проходят через центр гомотетии.

Если же прямая или плоскость проходят через центр гомотетии, то они отображаются в себя.

• Иррациональные числа
• Действительные числа
• Решение уравнений высших степеней
• Системы неравенств
• Уравнения и неравенства
• Уравнения и неравенства содержащие знак модуля
• Уравнение
• Метод математической индукции

При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org

Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи

Сайт пишется, поддерживается и управляется коллективом преподавателей

Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.

Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.

Видео:11 класс, 1 урок, Прямоугольная система координат в пространствеСкачать

Прямоугольные координаты (прямоугольная система координат)

Видео:Прямоугольная система координат в пространстве. 11 класс.Скачать

Определение прямоугольной системы координат

Аффинная система координат называется прямоугольной , если ее базис ортонормированный. Выбирая стандартные базисы (см. разд.1.3.5), получаем:

— прямоугольную систему координат на прямой — это точка и единичный вектор на прямой. Точки и (рис.2.4) на координатной оси обозначаются и ;

— прямоугольную систему координат на плоскости — это точка и два взаимно перпендикулярных единичных вектора и на плоскости (вектор — первый базисный вектор, a — второй; пара векторов — правая). Координатные оси (абсцисс) и (ординат) разбивают плоскость на 4 части, называемые квадрантами (четвертями) (рис.2.5). Точка , например, принадлежит четверти;

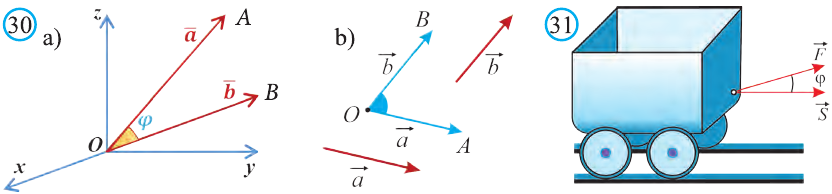
— прямоугольную систему координат в пространстве — это точка и три попарно перпендикулярных единичных вектора (вектор — первый базисный вектор, — второй, а — третий; тройка векторов — правая). Координатные оси обозначаются: — ось абсцисс, — ось ординат, — ось аппликат. Координатные плоскости , проходящие через пары координатных осей, разбивают пространство на 8 октантов (рис.2.6). Точка , например, принадлежит октанту.

Прямоугольные системы координат обозначают также указанием начала координат и координатных осей, например, .

Координаты векторов и точек в прямоугольной системе координат называются прямоугольными координатами .

Координатами вектора в прямоугольной системе координат называются коэффициенты в разложении вектора по стандартному базису (см. разд. 1.3.5).

Координатами точки в прямоугольной системе координат называются координаты ее радиус-вектора в стандартном базисе. В пространстве это коэффициенты в разложении , на плоскости — коэффициенты в разложении , на прямой — коэффициент в разложении . Прямоугольные координаты точки (или ее радиус-вектора) можно представить координатным столбцом:

1. В прямоугольной системе координат расстояние между точками и находится по формуле

Для координатной плоскости и координатной прямой соответственно получаем

2. Ориентированной площадью треугольника называется его площадь , взятая со знаком плюс, если ориентация пары векторов правая, и со знаком минус, если ориентация — левая. Если на плоскости известны прямоугольные координаты вершин , треугольника , то его ориентированная площадь вычисляется по формуле

Действительно, по свойствам определителя (см. разд.П.6) получаем половину ориентированной площади параллелограмма, построенного на векторах и (см. разд.1.5.3):

3. Ориентированным объемом тетраэдра (треугольной пирамиды) называется её объем, взятый со знаком плюс, если ориентация тройки векторов правая, и со знаком минус, если ориентация — левая. Если известны прямоугольные координаты вершин , , , тетраэдра , то его ориентированный объем вычисляется по формуле

Действительно, вычитая первую строку определителя из остальных строк и раскладывая затем определитель по последнему столбцу, получаем , т.е. одну шестую ориентированного объема параллелепипеда, построенного на векторах .

Пример 2.2. Известны прямоугольные координаты вершин треугольника (рис.2.7). Требуется найти:

а) длину медианы ;

б) длину биссектрисы ;

в) высоту , опущенную из вершины .

Решение. а) Учитывая пункт 3 замечаний 2.1, находим координаты точки — середины стороны :

Учитывая пункт 1 замечаний 2.2, получаем:

б) Найдем координаты точки , которая делит сторону в отношении (свойство биссектрисы треугольника). Так как и , то, учитывая пункт 2 замечаний 2.1 , находим , т.е. .

в) Учитывая пункт 2 замечаний 2.2, находим ориентированную площадь треугольника :

Следовательно, площадь этого треугольника , тогда , поскольку .

Пример 2.3. Известны прямоугольные координаты вершин треугольной пирамиды . Требуется найти:

а) длину отрезка , соединяющего вершину пирамиды с точкой пересечения медиан грани (см. рис.2.3);

б) объем пирамиды.

Решение. а) Координаты точки найдены в примере 2.1: . Поэтому

б) Найдем ориентированный объем пирамиды по формуле пункта 3 замечаний 2.2. Вычитая первую строку из остальных строк и раскладывая определитель по последнему столбцу, получаем

Видео:Прямоугольная система координат в пространстве. Практическая часть. 11 класс.Скачать

Векторы в пространстве и метод координат

Существует два способа решения задач по стереометрии

Первый — классический — требует отличного знания аксиом и теорем стереометрии, логики, умения построить чертеж и свести объемную задачу к планиметрической. Способ хорош тем, что развивает мозги и пространственное воображение.

Другой метод — применение векторов и координат. Это простые формулы, алгоритмы и правила. Он очень удобен, особенно когда времени до экзамена мало, а решить задачу хочется.

Если вы освоили векторы на плоскости и действия с ними — то и с векторами в пространстве разберетесь. Многие понятия окажутся знакомыми.

Видео:Координаты на плоскости и в пространстве. Вебинар | МатематикаСкачать

Система координат в пространстве

Выберем начало координат. Проведем три взаимно перпендикулярные оси X, Y и Z. Зададим удобный масштаб.

Получилась система координат в трехмерном пространстве. Теперь каждая его точка характеризуется тремя числами — координатами по X, Y и Z. Например, запись M(−1; 3; 2) означает, что координата точки M по X (абсцисса) равна −1, координата по Y (ордината) равна 3, а координата по Z (аппликата) равна 2.

Векторы в пространстве определяются так же, как и на плоскости. Это направленные отрезки, имеющие начало и конец. Только в пространстве вектор задается тремя координатами x, y и z:

Как найти координаты вектора? Как и на плоскости — из координаты конца вычитаем координату начала.

Длина вектора в пространстве – это расстояние между точками A и B. Находится как корень квадратный из суммы квадратов координат вектора.

Пусть точка M – середина отрезка AB. Ее координаты находятся по формуле:

Для сложения векторов применяем уже знакомые правило треугольника и правило параллелограмма

Сумма векторов, их разность, произведение вектора на число и скалярное произведение векторов определяются так же, как и на плоскости. Только координат не две, а три. Возьмем векторы и .

Произведение вектора на число:

Скалярное произведение векторов:

Косинус угла между векторами:

Последняя формула удобна для нахождения угла между прямыми в пространстве. Особенно если эти прямые – скрещиваются. Напомним, что так называются прямые, которые не параллельны и не пересекаются. Они лежат в параллельных плоскостях.

1. В кубе ABCDA₁B₁C₁D₁ точки E и K — середины ребер соответственно A₁B₁ и B₁C₁. Найдите косинус угла между прямыми AE и BK.

Если вам достался куб — значит, повезло. Он отлично вписывается в прямоугольную систему координат. Строим чертеж:

Длина ребра куба не дана. Какой бы она ни была, угол между AE и BK от нее не зависит. Поэтому возьмем единичный куб, все ребра которого равны 1.

Прямые AE и BK — скрещиваются. Найдем угол между векторами и . Для этого нужны их координаты.

Запишем координаты векторов:

и найдем косинус угла между векторами и :

2. В правильной четырехугольной пирамиде SABCD, все ребра которой равны 1, точки E, K — середины ребер SB и SC соответственно. Найдите косинус угла между прямыми AE и BK.

Лучше всего выбрать начало координат в центре основания пирамиды, а оси X и Y сделать параллельными сторонам основания.

Координаты точек A, B и C найти легко:

Из прямоугольного треугольника AOS найдем

Координаты вершины пирамиды:

Точка E — середина SB, а K — середина SC. Воспользуемся формулой для координат середины отрезка и найдем координаты точек E и K.

Найдем координаты векторов и

и угол между ними:

Покажем теперь, как вписать систему координат в треугольную призму:

3. В правильной треугольной призме ABCA₁B₁C₁, все ребра которой равны 1, точка D — середина ребра A₁B₁. Найдите косинус угла между прямыми AD и BC₁

Пусть точка A — начало координат. Возьмем ось X параллельно стороне BC, а ось Y перпендикулярно ей. Другими словами, на оси Y будет лежать отрезок AH, являющийся высотой треугольника ABC. Нарисуем отдельно нижнее основание призмы.

Запишем координаты точек:

Точка D — середина A₁B₁. Значит, пользуемся формулами для координат середины
отрезка.

Найдем координаты векторов и , а затем угол между ними:

Смотрите, как легко с помощью векторов и координат найти угол между прямыми. А если требуется найти угол между плоскостями или между прямой и плоскостью? Для решения подобных задач нам понадобится уравнение плоскости в пространстве.

Видео:Координаты вектора в пространстве. 11 класс.Скачать

Плоскость в пространстве задается уравнением:

Здесь числа A, B и C — координаты вектора, перпендикулярного этой плоскости. Его называют нормалью к плоскости.

Вместо x, y и z можно подставить в уравнение координаты любой точки, принадлежащей данной плоскости. Получится верное равенство.

Плоскость в пространстве можно провести через любые три точки, не лежащие на одной прямой. Поэтому для того, чтобы написать уравнение плоскости, берем координаты трех принадлежащих ей точек. Подставляем их по очереди в уравнение плоскости. Решаем полученную систему.

Покажем, как это делается.

Напишем уравнение плоскости, проходящей через точки M (1; 0; 1), N (2; −2; 0) и K (4; 1; 2).

Уравнение плоскости выглядит так:

Подставим в него по очереди координаты точек M, N и K.

То есть A + C + D = 0.

Аналогично для точки K:

Получили систему из трех уравнений:

В ней четыре неизвестных: A, B, C и D. Поэтому одну из них мы выберем сами, а другие выразим через нее. Правило простое — вместо одной из переменных можно взять любое число, не равное нулю.

Пусть, например, D = −2. Тогда:

Выразим C и B через A и подставим в третье уравнение:

Решив систему, получим:

Уравнение плоскости MNK имеет вид:

Умножим обе части уравнения на −3. Тогда коэффициенты станут целыми:

Вектор — это нормаль к плоскости MNK.

Уравнение плоскости, проходящей через заданную точку имеет вид:

Угол между плоскостями равен углу между нормалями к этим плоскостям:

Не правда ли, знакомая формула? Скалярное произведение нормалей поделили на произведение их длин.

Заметим, что при пересечении двух плоскостей вообще-то образуется четыре угла.

Мы берем меньший из них. Поэтому в формуле стоит модуль скалярного произведения — чтобы косинус угла был неотрицателен.

4. В кубе ABCDA₁B₁C₁D₁ точки E и F — середины ребер соответственно A₁B₁ и A₁D₁. Найдите тангенс угла между плоскостями AEF и BDD₁.

Строим чертеж. Видно, что плоскости AEF и BDD₁ пересекаются где-то вне куба. В классическом решении пришлось бы строить линию их пересечения. Но векторно-координатный метод значительно всё упрощает. Не будем ломать голову над тем, по какой прямой пересекаются плоскости. Просто отметим координаты нужных нам точек и найдем угол между нормалями к плоскостям AEF и BDD₁.

Сначала — нормаль к плоскости BDD₁. Конечно, мы можем подставить координаты точек B, D и D₁ в уравнение плоскости и найти коэффициенты, которые и будут координатами вектора нормали. А можем сделать хитрее — увидеть нужную нормаль прямо на чертеже. Ведь плоскость BDD₁ — это диагональное сечение куба. Вектор перпендикулярен этой плоскости.

Итак, первый вектор нормали у нас уже есть:

Напишем уравнение плоскости AEF.

Берем уравнение плоскости и по очереди подставляем в него, вместо x, y и z, соответствующие координаты точек A, E и F.

Пусть С = -1. Тогда A = B = 2.

Уравнение плоскости AEF:

Нормаль к плоскости AEF:

Найдем угол между плоскостями:

5. Основание прямой четырехугольной призмы BCDA₁B₁C₁D₁ — прямоугольник ABCD, в котором AB = 5, AD = √33. Найдите тангенс угла между плоскостью грани AA₁D₁D и плоскостью, проходящей через середину ребра CD перпендикулярно прямой B₁D, если расстояние между прямыми A₁C₁ и BD равно √3.

Эта задача наглядно показывает, насколько векторный метод проще классического. Попробуйте, для разнообразия, построить необходимые сечения и провести все доказательства — как это делается в «классике» 🙂

Строим чертеж. Прямую четырехугольную призму можно по-другому назвать «параллелепипед».

Замечаем, что длина и ширина параллелепипеда у нас есть, а вот высота — вроде не дана. Как же ее найти?

«Расстояние между прямыми A₁C₁ и BD равно √3». Прямые A₁C₁ и BD скрещиваются. Одна из них — диагональ верхнего основания, другая — диагональ нижнего. Вспомним, что расстояние между скрещивающимися прямыми равно длине их общего перпендикуляра. Общий перпендикуляр к A₁C₁ и BD — это, очевидно, OO₁, где O — точка пересечения диагоналей нижнего основания, O₁ — точка пересечения диагоналей верхнего. А отрезок OO₁ и равен высоте параллелепипеда.

Плоскость AA₁ D₁ D — это задняя грань призмы на нашем чертеже. Нормаль к ней — это любой вектор, перпендикулярный задней грани, например, вектор или, еще проще, вектор .

Осталась еще «плоскость, проходящая через середину ребра CD перпендикулярно прямой B₁D». Но позвольте, если плоскость перпендикулярна прямой B₁D — значит, B₁D и есть нормаль к этой плоскости! Координаты точек B₁ и D известны:

Координаты вектора — тоже:

Находим угол между плоскостями, равный углу между нормалями к ним:

Зная косинус угла, находим его тангенс по формуле

Получим:

Ответ:

Угол между прямой m и плоскостью α тоже вычисляется с помощью скалярного произведения векторов.

Пусть — вектор, лежащий на прямой m (или параллельный ей), — нормаль к плоскости α.

Находим синус угла между прямой m и плоскостью α по формуле:

6. В кубе ABCDA₁B₁C₁D₁ точка E — середина ребра A₁B₁. Найдите синус угла между прямой AE и плоскостью BDD₁.

Как всегда, рисуем чертеж и выбираем систему координат

Находим координаты вектора .

Нужно ли нам уравнение плоскости BDD₁? В общем-то, без него можно обойтись. Ведь эта плоскость является диагональным сечением куба, а значит, нормалью к ней будет любой вектор, ей перпендикулярный. Например, вектор .

Найдем угол между прямой и плоскостью:

Ответ:

Расстояние от точки M с координатами x₀, y₀ и z₀ до плоскости α, заданной уравнением Ax + By + Cz + D = 0, можно найти по формуле:

7. В основании прямоугольного параллелепипеда BCDA₁B₁C₁D₁ лежит прямоугольник ABCD со сторонами AB = , AD = . Высота параллелепипеда AA₁ = . Найдите расстояние от точки A до плоскости A₁DB.

Построим чертеж и выпишем координаты точек:

Запишем уравнение плоскости A₁DB. Вы помните, как это делается — по очереди подставляем координаты точек A₁, D и B в уравнение A_x + B_e + C_z + D

Решим эту систему. Выберем

Тогда

Уравнение плоскости A₁DB имеет вид:

Дальше все просто. Находим расстояние от точки A до плоскости A₁DB:

В некоторых задачах по стереометрии требуется найти расстояние от прямой до параллельной ей плоскости. В этом случае можно выбрать любую точку, принадлежащую данной прямой.

📹 Видео

Частное положение точек. Точки принадлежащие к плоскостям проекции.Скачать

Прямоугольная система координат в пространстве. Координаты вектора. Видеоурок по геометрии 11 классСкачать

46. Прямоугольная система координат в пространствеСкачать

Геометрия 11 класс (Урок№1 - Координаты в пространстве. Система координат.)Скачать

Задача, которую боятсяСкачать

ПРЯМОУГОЛЬНАЯ СИСТЕМА КООРДИНАТ В ПРОСТРАНСТВЕ 11 классСкачать

Координаты точки и координаты вектора 1.Скачать

Вычисляем высоту через координаты вершин 1Скачать

Прямоугольная система координат. Координатная плоскость. 6 класс.Скачать

Координаты вектора. 9 класс.Скачать

Прямоугольная система координат в пространствеСкачать

Метод координат для ЕГЭ с нуля за 30 минут.Скачать

Длина отрезкаСкачать

Векторы. Метод координат. Вебинар | МатематикаСкачать