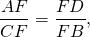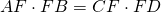Видео:№662 (исправлено) Хорды АВ и CD окружности пересекаются в точке Е. Найдите угол ВЕС, если ∪AD=54°Скачать
Ваш ответ
Видео:Геометрия Хорды AB и CD окружности не пересекаются, а прямые AB и CD пересекаются в точке M см. рисСкачать
Похожие вопросы
- Все категории
- экономические 43,277
- гуманитарные 33,618
- юридические 17,900
- школьный раздел 606,937
- разное 16,829
Популярное на сайте:
Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах.
Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте.
Как быстро и эффективно исправить почерк? Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.
Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью.
Видео:№662. Хорды АВ и CD окружности пересекаются в точке Е. Найдите угол ВЕС, если ∪AD=54°, ∪BC= 70°.Скачать
Хорды пересекаются
Если хорды пересекаются, как этот факт можно использовать при решении задач?
Теорема
(Свойство отрезков пересекающихся хорд (пропорциональность хорд окружности))
Произведения длин отрезков пересекающихся хорд, на которые эти хорды делятся точкой пересечения, есть число постоянное.
То есть, если хорды AB и CD пересекаются в точке F, то
AF ∙ FB=CF ∙ FD
Дано : окружность (O; R), AB и CD — хорды,
Доказать : AF ∙ FB=CF ∙ FD
1) Проведём отрезки BC и AD.
2) Рассмотрим треугольники AFD и CFB.
∠AFD=∠CFB (как вертикальные);
Следовательно, треугольники AFD и CFB подобны (по двум углам).
Из подобия треугольников следует пропорциональность соответствующих сторон:
то есть отрезки пересекающихся хорд пропорциональны.
По основному свойству пропорции:
Что и требовалось доказать .
При решении задач с пересекающимися хордами можно использовать не только вывод теоремы, но также полученный в ходе её доказательства факт, что пересекающиеся хорды образуют пары подобных треугольников.
Через точку M, лежащую внутри окружности, проведена хорда, которая делится точкой M на отрезки, длины которых равны 6 см и 16 см. Найти расстояние от точки M до центра окружности, если радиус окружности равен 14 см.
Дано : окружность (O; R), R=14 см, AB — хорда, M∈AB, AM=16 см, MB=6 см
Проведём через точку M диаметр CD.
По свойству отрезков пересекающихся хорд:
Пусть OM=x см (x>0). Так как радиус равен 14 см, то MD= (14-x) см, CM=(14+x) см.
Составим и решим уравнение:
Следовательно, расстояние от точки M до центра окружности равно 10 см.
В окружности проведены хорды AB и CD , пересекающиеся в точке F. Найти длину отрезка AC, если AF=6, DF=8, BD=20.
Дано : окружность (O; R), AB и CD — хорды,
В треугольниках AFC и BFD:
∠AFC=∠BFD (как вертикальные);
∠ACF=∠DBF (как вписанные углы, опирающиеся на одну хорду AD).
Следовательно, треугольники AFC и BFD подобны (по двум углам). Поэтому
Видео:Геометрия Хорды AB и CD окружности пересекаются в точке M (см. рис.). Докажите, что угол AMC = 1/2Скачать
Геометрия. 8 класс
Впишите правильный ответ.
Диаметр AB пересекает хорду CD в точке N, причём CN = 6, DN = 8, BN = 4. Найдите радиус окружности.
Впишите правильный ответ.
В окружности хорды MN и PK пересекаются в точке O1. Известно, что MO1 = 4 см, NO1 = 8 см, PO1 : O1K = 1 : 2. Найдите PO1. Ответ дайте в сантиметрах.
Установите соответствие между задачей и ответом к ней.
В окружности хорды MN и PK пересекаются
в точке A. Известно, что MA = 4, NA = 2,
PK = 6. Найдите, в каком отношении точка A
делит отрезок PK (это отношение меньше 1).
Хорды AB и CD пересекаются в точке F
так, что AF = 12, BF = 6, CF = 8.
Найдите, в каком отношении точка F
делит отрезок DС, считая от точки C.
📽️ Видео
№666. Хорды АВ и CD пересекаются в точке Е. Найдите ED, если: а) АЕ = 5, ВЕСкачать
№1035. В окружности проведены хорды АВ и CD, пересекающиеся в точке Е. Найдите острыйСкачать
Геометрия Докажите, что если хорды AB и CD окружности пересекаются в точке M, то AM٠MB = DM٠MCСкачать
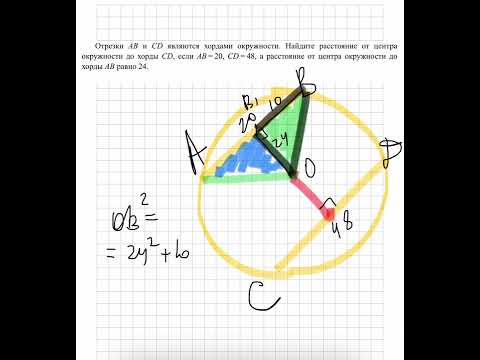
Отрезки AB и CD являются хордами окружности. Найдите расстояние от центра окружности до хорды CDСкачать
Геометрия Хорды AB и CD окружности пересекаются в точке M, AM = 6 см, BM = 14 см, CM = 12 смСкачать
Математика | 5 ЗАДАЧ НА ТЕМУ ОКРУЖНОСТИ. Касательная к окружности задачиСкачать
Всё про углы в окружности. Геометрия | МатематикаСкачать
Геометрия 8 класс (Урок№28 - Свойства хорд окружности.)Скачать
Геометрия Хорды AB и CD окружности пересекаются в точке M CM = 4 см DM = 6 см AM на 2 см больше BMСкачать
№166. Отрезки АВ и CD пересекаются в их общей середине О. Точки М и N — середины отрезков АС и BD.Скачать
Окружность, диаметр, хорда геометрия 7 классСкачать
Геометрия В окружности проведены хорды AB и CD, пересекающиеся в точке M. Дано: AM/МВ =5/7Скачать
Хорды AC и BD окружности пересекаются в точке P, BP=6, CP=8, DP=12. Найдите AP.Скачать
В окружности три хордыСкачать
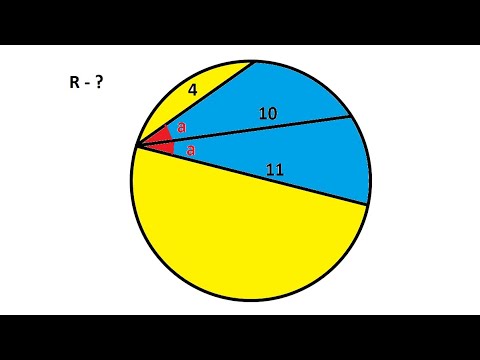
Окружность. 7 класс.Скачать
№144. Отрезки АВ и CD — диаметры окружности. Докажите, что: а) хорды BD и АС равны; б) хорды AD и ВССкачать
