Этот калькулятор оценивает число малых окружностей заданного радиуса r можно разместить внутри большой окружности заданного радиуса R.
Этот калькулятор выводит максимальное число малых окружностей заданного радиуса r можно разместить внутри большой окружности заданного радиуса R. Например это могут быть малые трубы внутри большой, провода в кабель канале, круги, вырезаемые из круговой же заготовки и так далее.
Вы можете подумать, что для решения такой задачи должна быть выведена формула, но на самом деле это не так — формулы нет. Эта задача относится к классу оптимизационных задач, а точнее, задач упаковки. Эта задача известна как Упаковка кругов в круге. Упаковка кругов в круге — это двумерная задача упаковки, целью которой является упаковка единичных кругов в как можно меньший круг. См. Упаковка кругов в круге.
Для этой задачи найденное решение еще и должно быть проанализировано на оптимальность. Статья в википедии по ссылке выше приводит первые 20 решений (иными словами, приводит минимальные радиусы больших окружностей вмещающих заданное число единичных окружностей. Между прочим, по умолчанию входные параметры калькулятора дают ответ 11 кругов, что соответствует следующей диаграмме:
Хорошей новостью является то, что есть проект в интернете, целиком посвященный задачам упаковки — сайт Packomania. На сегодняшний день он содержит все найденные решения, автор сайта, Экард Спехт (Eckard Specht), сам участвует в поиске решений, и большинство решений, на самом деле найдены им. Оттуда можно взять соотношения r к R для решений, позволяющих упаковать от 1 до 2600 окружностей внутри большой, с графическими диаграммами решения.
Соотношения r/R, приведенные на сайте и использует калькулятор ниже для поиска оптимального решения. Если соотношение не попадает в диапазон известных решений, калькулятор выдает ошибку.
Видео:Деление окружности на 3; 6; 12 равных частейСкачать

Круги в круге
Видео:Деление окружности на 12 равных частейСкачать

Задача
Чему равен наименьший радиус круга, в котором можно разместить без наложений 7 единичных кругов? Обоснуйте ваш ответ.
Примечание. Единичный круг — круг радиуса 1. «Без наложений» означает, что круги могут касаться, но не должны иметь общих внутренних точек.
Видео:Деление окружности на n- равные частиСкачать

Подсказка 1
Радиус равен 3, а «оптимальная картинка» выглядит именно так, как вы ее себе, скорее всего, и представили (рис. 1).
Видео:Деление окружности на 3 частиСкачать

Подсказка 2
Удобно избавиться от понятия «наложение», перейдя от этой задачи к такой:
Рассмотрим вместо кругов только их центры. В круг какого наименьшего радиуса можно их все уместить?
В «оптимальной картинке» все центры являются вершинами и центром правильного шестиугольника со стороной 2 (рис. 2). При этом расстояние между любыми двумя вершинами и центром такого шестиугольника тоже равно 2, поэтому все точки лежат в круге радиуса 2. Нужно обосновать, что все эти точки нельзя уместить в круг меньшего радиуса. Для этого попробуйте рассмотреть случаи, сколько именно (из шести отличных от центра) точек образуют выпуклый многоугольник.
Видео:Деление окружности на равные части с помощью циркуляСкачать

Решение
Будем действовать методом «от противного». Предположим, что шесть точек с попарным расстоянием 2 (или большим двух), удалось поместить в круг радиуса R BA и CH > CA. То есть при сдвиге A в H расстояния до точек B и C увеличились.
Наконец, если все точки лежат на единичной окружности, то они делят ее на 6 дуг, поэтому длина наименьшей из дуг не больше, чем 1/6 длины окружности, то есть не больше 2π/6. Это значит, что величина центрального угла этой дуги также не превышает 2π/6, а значит, расстояние между двумя точками, являющимися концами этой дуги, не больше 2sin(π/6) = 1.
Видео:Красивое деление окружности на 20 частей циркулемСкачать

Послесловие
Эта задача является примером огромного класса так называемых «минимаксных» задач вычислительной геометрии. В минимаксных задачах ищется наибольшее возможное значение какой-то величины, которая сама определена как наименьшее значение другой величины. В нашем случае минимаксная задача (к которой мы свели исходную) была такой: сначала среди всех 15 попарных расстояний между шестью точками в единичном круге выбирается наименьшее, а затем ищется такая конфигурация шести точек, для которой это расстояние будет максимальным из возможных.
Приведенное нами утверждение и его доказательство принадлежат замечательному американскому математику Рональду Грэхему (Ronald Graham), они опубликованы в 1968 году. Грэхем доказал даже более общую оценку для наименьшего расстояния d между какими-то из k точек, лежащих в единичном круге. Эта оценка имеет вид
(то есть d не превышает наибольшего из двух чисел — единицы и удвоенного синуса). Оценка Грэхема является оптимальной для 2 ≤ k ≤ 7, то есть существуют картинки, для которых достигаются значения из правой части этого неравенства. Для больших значений k указанная оценка неточна, поскольку она дает d ≤ 1, а на самом деле наибольшее из возможных значений минимального расстояния между точками строго меньше 1.
Естественное обобщение нашей задачи — поиск кругов наименьшего радиуса, в которые можно поместить N единичных кругов (или, что то же самое, поиск решения минимаксной задачи об N точках в единичном круге). В этом поиске усилия математиков сконцентрировались на двух направлениях — компьютерном моделировании и доказательствах оптимальности. Ниже на рис. 5 показаны несколько очевидных оптимальных картинок.
Оптимальность первых трех из них следует из приведенного выше результата Р. Грэхема. Оптимальность последней (для 8 кругов) была доказана в 1963 году голландцем Boele L. J. Braaksma в его диссертации под труднопроизносимым названием «Асимптотические расширения и аналитические продолжения для одного класса интегралов Барнса». Следующее продвижение, а также оптимальность вот такой вот картинки (рис. 6) с двумя внутренними кругами (для 10 кругов)
было получено немцем U. Pirl в 1969 году. Оптимальность аналогичной картинки для 11 кругов доказана еще на 25 лет позже, а для 12, 13 и 19 кругов — еще позже (последний из результатов — в 2003 году).
И. всё. Остальные результаты об упаковке кругов в круг на сегодняшний день находятся в состоянии «оптимальность предполагается, но не доказана». Так что просто полюбуйтесь на картинки (рис. 7) с доказанной оптимальностью (N = 12 и N = 19) и оцените: всего каких-то 15 лет назад это была терра инкогнита, обе задачи еще ждали своего решателя.
А следующие две картинки (для N = 14 и N = 15 соответственно) являются этой самой «инкогнитой» и сейчас (рис. 8). Дерзайте.
См. также:
1) Circle packing in a circle («Упаковка кругов в круг»). Достаточно детальная статья английской Википедии.
2) Circles in Circles. Страничка Эрика Фридмана, откуда мы позаимствовали большую часть иллюстраций. Там же на соседних страницах packing center рассказано о других задачах упаковки.
3) K. A. Dowsland, M. Gilbert, G. Kendall. A local search approach to a circle cutting problem arising in the motor cycle industry (PDF, 346 Кб). Статья в научном журнале Operational Research Society — международного сообщества, занимающегося исследованием операций, то есть научной дисциплиной, чья основная задача — обоснование оптимальности применения каких-либо научных достижений на практике.
В статье объясняется, как можно оптимизировать изготовление «звездочек» и других профилированных колёс (для зубчатых передач и др.) при производстве велосипедов и мотоциклов. С точки зрения математики — абсолютно ничего нового, но связь с практикой очень забавна. Интересно, появится ли когда-нибудь подобная статья для домохозяек — об оптимизации раскладывания котлет на сковородке?
Видео:Деление окружности на пять равных частей. Урок 7. (Часть 1. ГЕОМЕТРИЧЕСКИЕ ПОСТРОЕНИЯ)Скачать

Всё про окружность и круг
Окружность — это геометрическое место точек плоскости, равноудаленных от некоторой заданной точки (центра окружности). Расстояние между любой точкой окружности и ее центром называется радиусом окружности (радиус обозначают буквой R).
Значит, окружность — это линия на плоскости, каждая точка которой расположена на одинаковом расстоянии от центра окружности.
Кругом называется часть плоскости, ограниченная окружностью и включающая ее центр.
Отрезок, соединяющий две точки окружности, называется хордой. Хорда, проходящая через центр окружности, представляет собой диаметр. Диаметр окружности равен ее удвоенному радиусу: D = 2R.
Точка пересечения двух хорд делит каждую хорду на отрезки, произведение которых одинаково: a1a2 = b1b2
Касательная к окружности всегда перпендикулярна радиусу, проведенному в точку касания.
Отрезки касательных к окружности, проведенные из одной точки, равны: AB = AC, центр окружности лежит на биссектрисе угла BAC.
Квадрат касательной равен произведению секущей на ее внешнюю часть
Центральный угол — это угол, вершина которого совпадает с центром окружности.
Дугой называется часть окружности, заключенная между двумя точками.
Мерой дуги (в градусах или радианах) является центральный угол, опирающийся на данную дугу.
Вписанный угол это угол, вершина которого лежит на окружности, а cтороны угла пересекают ее.
Вписанный угол равен половине центрального, если оба угла опираются на одну и ту же дугу окружности.
Внутренние углы, опирающиеся на одну и ту же дугу, равны.
Сектором круга называется геометрическая фигура, ограниченная двумя радиусами и дугой, на которую опираются данные радиусы.
Периметр сектора: P = s + 2R.
Площадь сектора: S = Rs/2 = ПR 2 а/360°.
Сегментом круга называется геометрическая фигура, ограниченная хордой и стягиваемой ею дугой.
🌟 Видео
Деление окружности на 6 равных частейСкачать

Длина окружности. Математика 6 класс.Скачать

Как разделить окружность на равные части!Скачать

Деление окружности на равные частиСкачать

Деление окружности на равные части. Урок 6. (Часть 1. ГЕОМЕТРИЧЕСКИЕ ПОСТРОЕНИЯ)Скачать

Деление окружностиСкачать

Быстро и легко определяем центр любой окружностиСкачать

Окружность. 7 класс.Скачать

Видеоуроки по КОМПАС 3D. Урок 1 Деление окружности на равные частиСкачать

5 класс, 22 урок, Окружность и кругСкачать

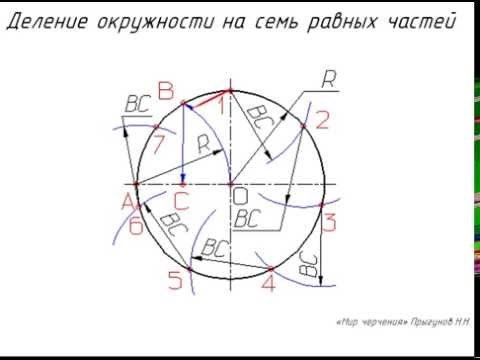
Деление окружности на 7 частейСкачать
Как разделить окружность на 6 частей. How to divide a circle into 6 partsСкачать

Деление окружности на N равных частей. Урок 8. (Часть 1. ГЕОМЕТРИЧЕСКИЕ ПОСТРОЕНИЯ)Скачать
















