Чертеж параллелограмма построенного на векторах

Видео:Найдите площадь параллелограмма, построенного на векторахСкачать

Четырехугольник и вектор на плоскости

Каждый школьник понимает, что параллелограмм является специальным видом плоских четырехугольников. Эта фигура состоит из двух пар параллельных пересекающихся отрезков. Она обладает следующими важными свойствами:

• ее противоположные стороны и углы равны друг другу;
• сумма всех четырех углов составляет 360 градусов;
• если просуммировать лишь два смежных (прилежащих к одной стороне) угла, то получится значение 180 градусов;
• любая диагональ делит фигуру на две равные части (треугольники);
• пересечение диагоналей происходит в точке, которая является геометрическим и массовым центром параллелограмма;
• любая секущая, которая проходит через геометрический центр, делит фигуру на две равные по площади части.

Специальные типы

Исходя из определения параллелограмма, как четырехугольника с параллельными и равными по длине противоположными сторонами, можно привести несколько видов фигуры, которые обладают высокой симметрией по отношению к ряду элементарных операций. Это следующие геометрические типы:

1. Квадрат. Все четыре стороны его равны по длине между собой, а углы составляют 90 градусов. Он является фигурой с достаточно высокой симметрией, и его площадь вычисляется просто как квадрат длины любой его стороны.
2. Прямоугольник. Еще один вид параллелограмма, все углы которого являются прямыми. Его симметрия несколько ниже, чем у квадрата, поскольку длины сторон равны лишь попарно. Площадь фигуры можно вычислить, перемножив длины смежных сторон.
3. Ромб. Специальный геометрический тип параллелограмма, который характеризуется тем, что длины всех его сторон являются одинаковыми. Углы фигуры попарно равны и отличаются от 90 градусов (два тупых и два острых).

Направленные отрезки и операция умножения

Площадь параллелограмма через векторы рассчитать легко, если знать понятие направленного отрезка и уметь работать с соответствующими математическими операциями. Поскольку любая точка на плоскости может быть представлена в виде набора двух координат в декартовой прямоугольной системе, то для P и Q можно записать:

P (x1, y1); Q (x2, y2).

Где числа x1, y1, x2 и y2 являются соответствующими координатами для точек P и Q по осям абсцисс и ординат. Чтобы получить вектор PQ-, который будет направлен из P в точку Q, необходимо из координат Q попарно вычесть значения для P:

PQ- = Q — P = (x2-x1, y2-y1).

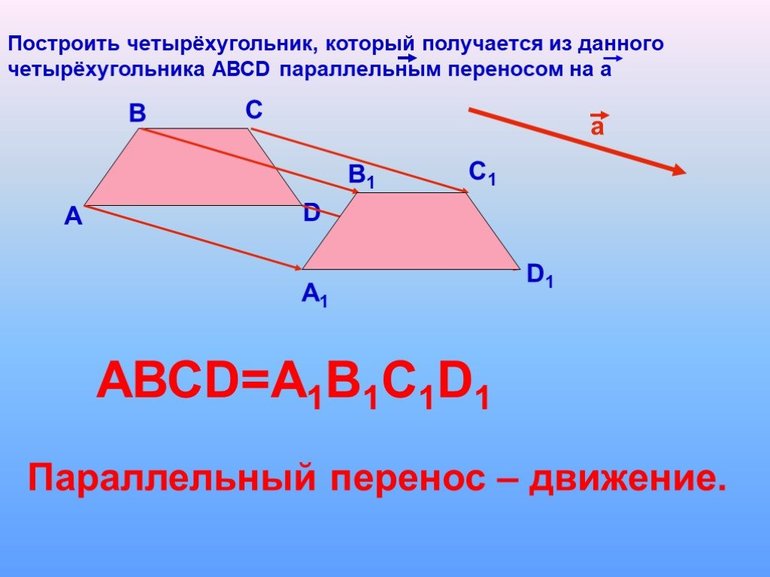
Координаты направленного отрезка на плоскости определяются так же, как и для точки, набором из двух чисел. Чтобы построить такой вектор в системе координат, необходимо его начало расположить в точке (0, 0), а конец со стрелкой будет располагаться в точке (x2-x1, y2-y1). Из этой геометрической интерпретации следует, что существует бесконечное множество направленных отрезков, которые эквивалентны между собой. Получаются они друг из друга с помощью параллельного переноса по всей плоскости координат.

Как и числа, направленные отрезки также можно складывать между собой, вычитать и умножать. Рассматривая вопрос построение параллелограмма на векторах и нахождения его площади, необходимо изучить свойства векторного произведения. Оно представляет собой вектор, перпендикулярный плоскости, в которой лежат исходные направленные отрезки. Пусть a- и b- необходимо умножить векторно. Результатом произведения будет следующий вектор c-:

c- = [a-*b-] = |a-|*|b-|*sin (alfa).

Здесь alfa — угол между a- и b-, а |a-| и |b-| — длины соответствующих направленных отрезков.

Направление c- принято определять с помощью правила правой руки. Оно гласит: если четыре пальца ладони направить от конца первого умножаемого вектора к концу второго, то оттопыренный большой палец укажет направление результирующего векторного умножения.

Координаты вектора c- можно вычислить также, если воспользоваться понятием определителя матрицы. Пусть a- имеет координаты (a1, a2), а b- = (b1, b2), тогда формула для определения c- запишется в следующем виде:

c- = (0, 0, (a1*b2-b1*a2)).

Вектор c- имеет первые две нулевые координаты, поскольку он перпендикулярен плоскости, в которой находятся a- и b-.

Видео:Площадь параллелограмма, построенного на данных векторахСкачать

Формула площади из геометрии

Чтобы получить формулу площади параллелограмма на векторах, необходимо вспомнить, как рассчитывается эта величина для треугольника. Если известна одна сторона (основание a) и высота, которая на нее опущена (h), то получается простое выражение:

Где S3 — площадь треугольника. Поскольку две таких плоских фигуры, которые соединены одной из своих сторон, образуют четырехугольник-паралелограм, то для него рассмотренную величину можно вычислить по формуле:

Пусть вторая сторона параллелограмма равна b, тогда с высотой h она связана через определение тригонометрической функции синус:

sin (alfa) = h/b => h = b*sin (alfa).

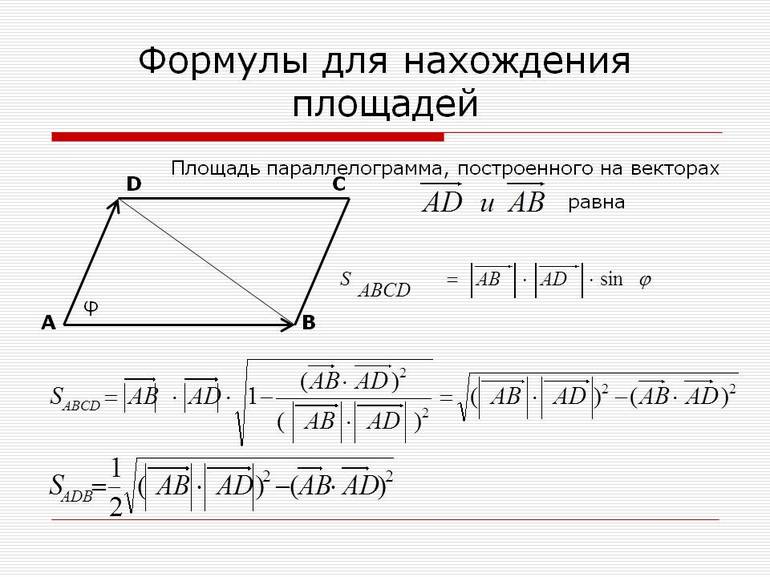
Если подставить это равенство в выражение для S4, то нахождение площади фигуры сведется к расчету произведения двух его смежных сторон и синуса угла между ними:

Поскольку угол alfa изменяется от 0 до 180 градусов, то функция синус всегда имеет положительное значение. Этой формулой часто пользуются на практике. Распространение инженерных калькуляторов позволяет быстро и с высокой точностью вычислять синусы любых углов.

Построение параллелограмма

Определить площадь четырехугольника с попарно параллельными сторонами можно не только через длины его сторон. Если внимательно посмотреть на формулу для S4, то можно заметить, что она идентична по виду векторному произведению направленных отрезков.

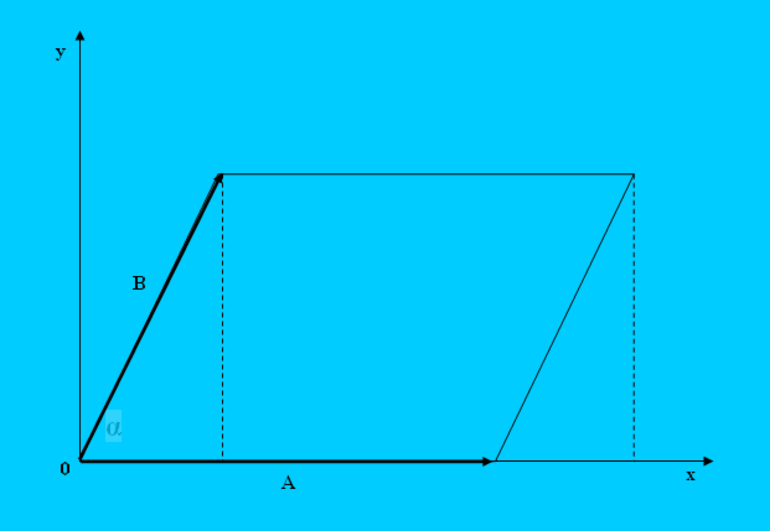
Пусть имеется два вектора a- и b-. Угол между ними равен alfa. Если их начала совместить в одной точке на плоскости, затем, от конца a- продолжить вектор b-, а из b- начертить a-, то получится параллелограмм, побудованый на a- и b-. Очевидно, что модуль векторного произведения этих направленных отрезков будет равен площади полученной фигуры:

S4 = a*b*sin (alfa) = |[a-*b-]|.

Применяя координатное выражение этого произведения, можно записать следующую формулу для площади:

Где a- = (a1,a2) и b-=(b1,b2). Знак модуля необходим потому, что по правилу правой руки могут получаться отрицательные векторы. Площадь же является всегда величиной положительной.

Преимущество последней записанной формулы для S4 по сравнению с выражением, где необходимо знать длины и углы, заключается в том, что ее использование не требует никаких предварительных вычислений. Достаточно лишь знать координаты конца и начала образующих параллелограмм векторов.

Задача с тремя точками

Чтобы научиться пользоваться записанной простой формулой, следует решить простую задачу. Имеется три точки, координаты которых следующие:

На вершинах этих точек следует построить параллелограмм, а затем, рассчитать его площадь S4.

Задачу проще всего решать через использование векторов. Выберем произвольную точку из трех заданных. Пусть это будет A. Из нее выходит два вектора: AB- и AC-. Их координаты определяются таким образом:

AB- = (2−1, 0-(-1)) = (1, 1); AC- = (-4−1, 3- (-1)) = (-5, 4).

Чтобы определить площадь параллелограмма на этих векторах, следует применить формулу для их векторного произведения. Порядок умножения направленных отрезков не имеет значения. Получается следующий результат:

S4 = [AB-*AC-] = 1*4 — (-5)*1 = 9.

Результат получен в единицах квадратных соответствующей двумерной системы координат.

Если была выбрана в качестве исходной не точка A, а B или C, то получился бы тот же результат, что можно доказать, проделав аналогичные вычисления.

Видео:Площадь параллелограмма по векторамСкачать

Диагонали фигуры

Некоторые задачи по геометрии параллелограммов в качестве начального условия предлагают знание одной или двух его диагоналей. По этим данным необходимо вычислить характеристики всей фигуры, включая ее площадь. Решать такие задачи также удобно с использованием понятия векторов.

Если дана диагональ, выраженная вектором f- и основание, представленное направленным отрезком a-, то формула для площади параллелограмма имеет вид:

Где beta — угол между a- и f-. Видно, что это выражение не отличается от предыдущих для S4. Доказать его справедливость несложно, если рассмотреть построенные на указанных векторах треугольники и использовать признаки их подобия.

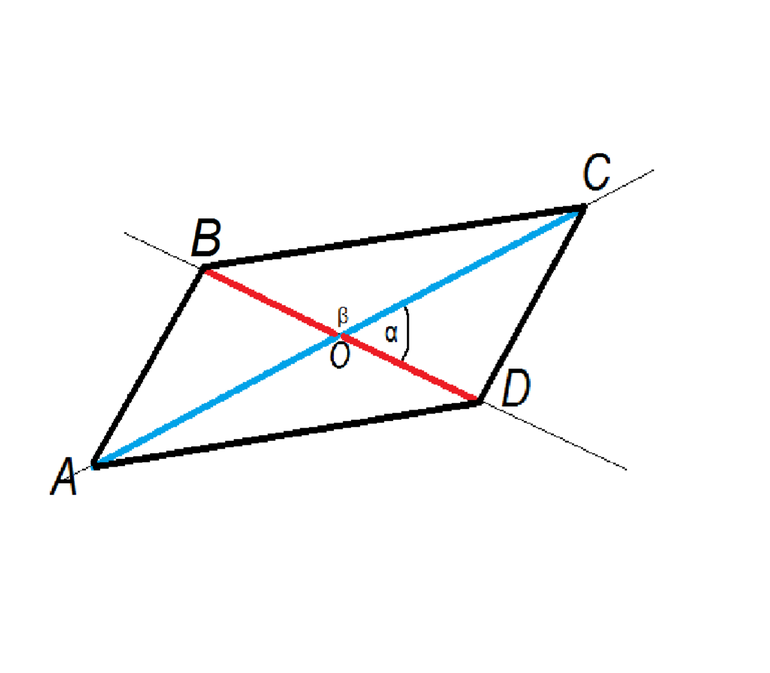
Другой случай, когда даны обе диагонали параллелограмма f- и e-. Воспользовавшись геометрическими построениями на плоскать, можно показать справедливость следующего выражения:

Здесь teta — это угол пересечения e- и f-. Таким образом, чтобы вычислить площадь параллелограмма, диагоналями которого служат вектора, следует вычислить половину модуля их векторного произведения.

Видео:как найти площадь параллелограмма построенного на векторахСкачать

Пример решения

Все разнообразие задач на определение площади параллелограмма сводится к знанию единственной формулы векторного произведения. Пусть известны две диагонали фигуры. Они имеют координаты:

Чтобы определить величину S4, достаточно без промежуточных вычислений воспользоваться формулой векторного произведения заданных направленных отрезков:

В связи с развитием интернета, всегда можно использовать калькулятор-онлайн для расчета величины S4. Соответствующий электронный ресурс можно знайти, воспользовавшись любой поисковой системой в браузере.

Видео:§20 Нахождение объёма параллелипипедаСкачать

Трехмерное пространство

В пространственной системе координат каждый вектор задается тремя числами, поэтому их векторное произведение c- также будет представлять набор трех цифр. Построенный в пространстве параллелограмм на двух векторах будет иметь площадь, равную длине направленного отрезка c-. Для расчета его модуля следует использовать известное выражение: сумма квадратов трех координат под корнем.

Таким образом, площадь параллелограмма проще всего вычислять, используя операцию умножения векторов. Этот метод является универсальным не только для задач на плоскости, но и для решения проблем в трехмерной системе координат.

Видео:Найти угол между векторами и площадь параллелограмма, построенного на этих векторахСкачать

Метод параллелограмма: примеры, решенные упражнения

Видео:Задача 4. Вычислить площадь параллелограмма, построенного на векторах.Скачать

Содержание:

В метод параллелограмма это графический метод сложения двух векторов на плоскости. Он часто используется, чтобы найти равнодействующую двух сил, приложенных к телу, или двух скоростей, как в случае пловца, который пытается пересечь реку перпендикулярно и отклоняется течением.

Чтобы построить параллелограмм, начала добавляемых векторов в масштабе должны совпадать в одной точке.

Затем параллельно каждому вектору проводят вспомогательные линии, доходящие до крайности другого, как показано на рисунке выше.

Сумма или результирующий вектор, также называемый чистой силой, является вектором F_сеть, который получается путем рисования вектора, идущего от общего начала координат F₁ Y F₂, до точки пересечения вспомогательных параллельных прямых. На схеме рисунка они представлены пунктирными линиями.

Метод получил свое название от фигуры, которая образована слагаемыми векторами и вспомогательными линиями, которая в точности представляет собой параллелограмм. Главная диагональ параллелограмма — это вектор суммы.

Очень важно отметить, что порядок, в котором размещаются слагаемые векторы, вообще не изменяет сумму, так как эта операция между векторами является коммутативной.

Видео:Найдите длины диагоналей параллелограмма, построенного на векторах a=(1;-1;-4) и b=(-5;3;8)Скачать

Пример пошагового метода параллелограмма

На следующем изображении показаны векторы v Y или в условных единицах. Вектор v измеряет 3,61 единицы и образует угол 56,3 ° с горизонтом, в то время как или он измеряет 6,32 единицы и угол 18.4º относительно указанной опорной линии.

Мы собираемся найти его векторную сумму, используя метод параллелограмма.

Необходимо выбрать соответствующий масштаб, например, показанный на следующем рисунке, в котором плоскость разделена сеткой. Ширина квадрата соответствует одной (1) единице.

Поскольку векторы не изменяются при преобразовании, они располагаются так, чтобы их начало совпадало с началом системы координат (левое изображение).

Теперь давайте выполним следующие шаги:

1. Участок к концу вектора v сегментированная линия, параллельная вектору или.
2. Повторите процедуру, но на этот раз с концом вектора. или.
3. Нарисуйте главную диагональ, идущую от общего начала до точки пересечения сегментированных линий.

Результат виден на правом изображении, на котором появляется результирующий вектор. Р.

Если мы хотим узнать величину р, мы можем измерить его длину и сравнить с имеющимся у нас масштабом. Что касается его направления, то в качестве ориентиров можно использовать, например, горизонтальную или вертикальную ось.

При использовании горизонтальной оси или оси x угол, р форма с указанной осью измеряется транспортиром, и таким образом мы знаем направление р.

Кроме того, величина и направление р можно вычислить с помощью теорем косинусов и синусов, так как образовавшийся параллелограмм можно разделить на два равных треугольника, сторонами которых являются модули векторов или, v Y р. См. Рабочий пример 1.

Видео:2. Векторы в параллелограмме Решение задач №2Скачать

Частный случай: сумма перпендикулярных векторов

Когда векторы перпендикулярны друг другу, образующаяся фигура представляет собой прямоугольник. Модуль полученного вектора соответствует длине диагонали, которую легко вычислить с помощью теоремы Пифагора.

Видео:Математика без Ху!ни. Смешанное произведение векторовСкачать

Решенные упражнения

Видео:Площадь треугольника, построенного на векторахСкачать

— Упражнение 1

У нас есть вектор v, который имеет размер 3,61 единицы и составляет угол 56,3 ° с горизонтом, а вектор или, размер которого составляет 6,32 единицы и составляет угол 18,4 ° (рисунок 2). Определите модуль результирующего вектора р = или + v и направление, которое указанный вектор образует с горизонтальной осью.

Видео:1. Векторы и параллелограмм задачи №1Скачать

Решение

Метод параллелограмма применяется в соответствии с шагами, описанными выше, для получения вектора р. Как было сказано ранее, если векторы аккуратно нарисованы по шкале и с помощью линейки и транспортира, величина и направление р они измеряются прямо на чертеже.

Их также можно рассчитать напрямую, с помощью тригонометрии и свойств углов. Когда образованный треугольник не правильный, как в этом случае, применяется теорема косинусов, чтобы найти недостающую сторону.

В треугольнике справа стороны измеряют u, v и R. Чтобы применить теорему косинусов, необходимо знать угол между v Y или, который мы можем найти с помощью сетки, адекватно позиционируя углы, указанные в утверждении.

Этот угол равен α и состоит из:

α = (90-56.3º) + 90º +18.4º = 142.1º

Согласно теореме косинусов:

р 2 = v 2 + ты 2 — 2u⋅v⋅cos α = 3,61 2 + 6.32 2 — 2 × 3,61 × 6,32 × cos 142,1º = 88,98

Наконец, угол между р а по горизонтальной оси θ = 18,4 º + γ. Угол γ можно найти с помощью теоремы синусов:

грех α / R = грех γ / u

sin γ = v (sin α / R) = 3,61 x (sin 142,1º / 9,43)

θ = 18.4 º + 13.6 º = 32º

Видео:Решение, найти площадь параллелограмма, построенного на векторах a и b пример 3. Высшая математика.Скачать

— Упражнение 2.

Пловец собирается пересечь реку, плывя перпендикулярно течению с постоянной скоростью 2,0 м / с. Пловец стартует из точки А, но заканчивается в точке В, расположенной ниже по течению, из-за отклонившего его течения.

Если скорость течения составляет 0,8 м / с, и все скорости предполагаются постоянными, найдите скорость пловца, которую видит наблюдатель, стоящий на берегу.

Видео:Решение, найти площадь параллелограмма, построенного на векторах a и b пример 9Скачать

Решение

Наблюдатель, стоящий на берегу, увидит, как пловец отклоняется в зависимости от полученной скорости. V_р. Чтобы найти ответ, нам нужно векторно сложить скорость пловца относительно воды и скорость течения, которую мы называем V _Река:

V _р = V _пловец + V _Река

На рисунке, который не в масштабе, векторы были добавлены для получения V _р. В этом случае можно применить теорему Пифагора, чтобы получить его величину:

V_р 2 = 2.0 2 + 0.8 2 = 4.64

Направление, в котором пловец отклоняется от перпендикулярного направления, легко вычислить, учитывая, что:

θ = arctg (2 / 0,8) = 68,2º

Затем пловец отклоняется на 90º — 68,2º = 27,2º от своего первоначального направления.

Видео:Решение, вычислить площадь параллелограмма, построенного на векторах a=p+2q и b=3p−q пример 12Скачать

Ссылки

1. Бауэр, В. 2011. Физика для инженерии и науки. Том 1. Мак Гроу Хилл.
2. Бедфорд, 2000. А. Инженерная механика: Статика. Эддисон Уэсли.
3. Фигероа, Д. (2005). Серия: Физика для науки и техники. Том 1. Кинематика. Отредактировал Дуглас Фигероа (USB).
4. Джамбаттиста, А. 2010. Физика. 2-й. Эд. Макгроу Хилл.
5. Сирс, Земанский. 2016. Университетская физика с современной физикой. 14-го. Ред. Том 1.

Волновая энергия: история, как это работает, преимущества, недостатки

Временная стоимость денег: факторы, важность, примеры

Видео:Угол между векторами | МатематикаСкачать

Найти площадь параллелограмма, построенного на векторах: онлайн-калькулятор

Для вычисления площади параллелограмма, построенного на векторах, нужны значения этих векторов или координаты точек. Онлайн-калькулятор выдает подробное решение и ответ. В зависимости от введенных данных программа подбирает формулы для расчета в нужной последовательности.

Сервисом пользуются школьники и студенты, когда надо быстро найти площадь параллелограмма – на контрольной, зачете, экзамене. Также по готовому решению задачи удобно изучать новую тему.

1. В форме представления параллелограмма выберите способ «Двумя векторами сторон».
   
2. Введите значения векторов в соответствующие поля. Отправьте задание на вычисление кнопкой «Рассчитать».
   
3. Получаем решение и ответ.
   
   

1. В форме представления параллелограмма выберите способ «Координатами точек».
   
2. Введите координаты вершин в соответствующие поля. Отправьте задание на вычисление кнопкой «Рассчитать».
   
   
3. Получаем решение и ответ.
   
   
   

Видео:Решение, вычислить площадь параллелограмма, построенного на векторах a=3p+q и b=p−2q пример 14Скачать

Материалы, которые помогут вам лучше разобраться в теме:

Видео:§16 Нахождение площади параллелограммаСкачать

Как найти площадь параллелограмма

Чтобы найти площадь параллелограмма, построенного на векторах, необходимо вычислить произведение длин векторов и синуса угла между ними. В заданиях, где длины векторов неизвестны, а даны координаты векторов, необходимо произвести следующие вычисления:

1. Найти векторы a ⇀ и b ↔ по точкам.
2. Вычислить произведение векторов.
3. Рассчитать модуль вектора c → .
4. Высчитать площадь S = a → × b →

Использование онлайн-калькулятора позволяет не думать о выборе способа решения, а просто ввести данные и получить поэтапные вычисления и ответ. Такой вариант подойдет учащимся, их родителям, преподавателям, инженерам.

Сервис позволяет узнать, чему равна площадь параллелограмма и других фигур, а также решить задачи на любую тему по алгебре и геометрии. Для этого не придется платить, регистрироваться на сайте, долго ждать. Расчеты производятся онлайн. Вы можете осваивать новую тему или сверяться с собственным решением неограниченное количество раз.

Если тема осталась непонятной, напишите консультанту. Наш сотрудник подберет вам преподавателя по выгодной цене или организует онлайн-помощь на зачете.

💥 Видео

Решение, вычислить площадь параллелограмма построенного на векторах a и b пример 5 Высшая математикаСкачать

Найти площадь параллелограмма, построенного на векторах a=p−3q и b=p+2q; |p|=1/5, |q|=1 пример 16Скачать