Педальный треугольник проект 8 класс (2 видео)

Педальный треугольник

Исследовательская работа на тему «Педальный треугольник». В работе дано определение педального треугольника, включены несколько основных свойств педального треугольника и представлены задачи, которые удобно решать, используя эти свойства.

Содержание

Скачать:
Предварительный просмотр:
Подписи к слайдам:
Проект «Педальный треугольник»
Просмотр содержимого документа «Проект «Педальный треугольник»»
Презентация: Свойства педального треугольника. Точка Брокара.
Просмотр содержимого документа «Презентация: Свойства педального треугольника. Точка Брокара.»
📹 Видео

Видео:Задача на подобие треугольников. А ты сможешь решить? | TutorOnline | МатематикаСкачать

Скачать:

Вложение	Размер
исследовательская работа «Педальный треугольник»	260.37 КБ
презентация к защите	973.42 КБ

Видео:Геометрическое решение задачи из видео Бориса Трушина. Изогональное сопряжение.Педальный треугольникСкачать

Предварительный просмотр:

Исторический экскурс. . 5

Педальный треугольник и его свойства. 7

Практическая часть. 12

Список литературы и интернет-ресурсов. 16

Есть в математике нечто, вызывающее человеческий восторг.

Треугольник — одна из основных фигур, изучаемых в геометрии. В школьном курсе геометрии рассматриваются свойства и теоремы о произвольных, равносторонних, равнобедренных, прямоугольных треугольниках. Чтобы расширить геометрические представления о свойствах треугольника, познакомимся с педальным треугольником. Свойства педального треугольника позволяют решать сложные математические задачи просто, красиво и понятно.

Объект исследования: педальный треугольник.

Предмет исследования: свойства педального треугольника.

Цель работы: расширить геометрические представления о свойствах треугольника и рассмотреть их практическое применение при решении задач.

изучить педальный треугольник;
рассмотреть свойства педального треугольника и доказать самостоятельно некоторые из них;
рассмотреть задачи с применением свойств педального треугольника.

Гипотеза: если выяснить свойства педального треугольника и овладеть ими, то возникает объективная возможность для решения задач повышенной сложности.

частично-поисковый метод;
экспериментальный;
системно-сравнительный анализ.

Первый этап – теоретический. Поиск и изучение теоретического материала (литературы и Интернет-ресурсов) по теме «Педальный треугольник».
Второй этап – практический. Доказательство свойств педального треугольника и решение задач с их использованием.
Третий этап – заключительный. Систематизация и обобщение теоретического материала. Анализ решение задач. Формулировка выводов.

Треугольник – самая простая замкнутая прямолинейная фигура, одна из первых, свойства которых человек узнал еще в глубокой древности, так как эта фигура всегда имела широкое применение в практической жизни. Платон утверждал, что вообще вся “Поверхность состоит из треугольников”.

Треугольник — первая геометрическая фигура, встречающаяся в древних орнаментах. Изображения треугольников и задачи на треугольники встречаются во многих папирусах Древней Греции и Древнего Египта.

В Египте он символизировал триаду духовной воли, любви, интуиции и высшего разума человека, то есть его личность или душу. Прямоугольный треугольник применялся тысячелетия назад строителями египетских пирамид.

В более древних культурах нередко встречаются треугольники как формы декора на керамике, при этом с вершиной, направленной вниз, рассматриваются как «символы воды» (направление падающей капли), а с вершиной, направленной вверх, — как «символы огня» (направление пламени). Наложенные один на другой, оба они образуют шестиконечную звезду.

Ацтеки использовали изображение треугольника с вершиной наверху, соединенного с перевернутым треугольником, в качестве символа временного цикла.

Уже со времён палеолита и неолита в древнем искусстве очень широко распространяются изображения равностороннего треугольника:

— вожди племен североамериканских индейцев носили на груди символ власти: равносторонний треугольник.

— в Африке женщины украшали себя большими пластинами из равносторонних треугольников.

— у христиан равносторонний треугольник означает Троицу — Отца, Сына и Святого Духа.

Еще в древности стали вводить некоторые знаки для обозначения геометрических фигур. Древнегреческий ученый Герон (I век н.э.) впервые применил знак Δ вместо слова треугольник.

В западном искусстве композиционные схемы с треугольниками часто используются в архитектуре и в живописи.

В современности треугольники используются в различных конструкциях, требующих наибольшей прочности, например, при строительстве.

Треугольники используют в различных играх, например в бильярде или боулинге.

Треугольник есть среди музыкальных инструментов

Треугольник можно увидеть на небе.

Также известен Бермудский треугольник — район в Атлантическом океане, в котором происходят таинственные исчезновения морских и воздушных судов.

Педальный треугольник и его свойства

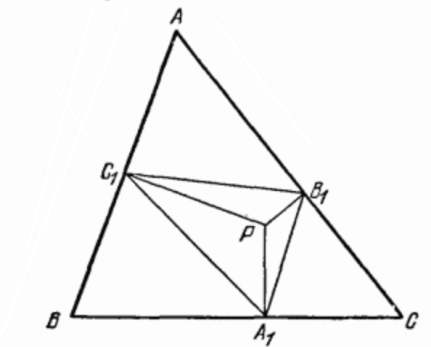
Пусть Р — любая точка внутри треугольника АВС, и пусть перпендикуляры, опущенные из точки Р на стороны ВС, СА, АВ треугольника, будут РА 1 , РВ 1 и РС 1 . Треугольник А 1 В 1 С 1 вершинами которого являются основания этих перпендикуляров, называется педальным треугольником треугольника АВС для «педальной точки» Р (рис.1).

Определение: Педальный треугольник — треугольник, вершинами которого являются основания перпендикуляров, опущенных из точки, находящейся внутри треугольника. А сама эта точка называется педальной точкой.

Рассмотрим некоторые свойства педального треугольника:

Теорема 1. Если расстояние от педальной точки до вершины треугольника АВС равны х, у, z, то длины сторон педального треугольника равны , где R – радиус описанной окружности.

Дано: треугольник АВС, Р – педальная точка. АР=х, ВР=у, СР=z, R – радиус описанной окружности.

Доказательство: Около каждого из полученных четырехугольников ВС 1 РА 1 , СВ 1 РА 1 , АС 1 РВ 1 можно описать окружность (по свойствам описанного четырехугольника). Прямые углы в точках С 1 и В 1 указывают на то, что эти точки лежат на окружности с диаметром АР, другими словами, точка Р лежит на окружности, описанной вокруг треугольника АВ 1 С 1 . Аналогично, точка Р лежит на окружностях, описанных вокруг треугольников СА 1 В 1 , ВС 1 А 1 .

Опишем окружность около четырехугольника АВ 1 РС 1 ; ее диаметром будет АР.

Пусть В 1 С 1 =а 1 , тогда на основании теоремы синусов 1 для треугольника С 1 АВ 1 : (1).

Применив теорему синусов к самому треугольнику АВС, получим (2).

Разделив почленно равенство (1) на равенство (2), получим: .

Аналогично: , где . А так как АР=х, ВР=у, СР=z, то длины сторон педального треугольника равны .Теорема доказана.

Замечание. Если точка Р является центром описанной окружности (х=у=z=R), то длины сторон педального треугольника равны .

Можно расширить условие нахождения педальной точки внутри треугольника. Тогда она может находиться и вне его. Если педальную точку взять на описанной около треугольника окружности, то треугольник «вырождается», а основания перпендикуляров, опущенных от данной точки к сторонам треугольника, лежат на одной прямой, которая называется прямой Симсона .

Теорема 2: Основания перпендикуляров, опущенных из точки на стороны треугольника, лежат на одной прямой тогда и только тогда, когда эта точка лежит на описанной окружности.

Открытие этой прямой долго приписывалось Роберту Симсону [1] , но в действительности она была открыта лишь в 1797 году Уильямом Уоллесом [2] . Поэтому наряду с традиционным названием этой прямой часто используется исторически более справедливое название прямая Уоллеса.

Теорема 3: Если из точки L внутри треугольника опущены перпендикуляры l a , l b , l c соответственно на стороны а, b, с треугольника, то (рис. 4).

Дано: треугольник АВС, а, b, с – стороны, L – педальная точка; l a , l b , l c — перпендикуляры соответственно на стороны а, b, с.

Доказать:

Доказательство: Соединим точку L c вершинами треугольника АВС. Треугольник АВС разобьется на три треугольника. Назовем площади этих треугольников S a , S b , S c . Тогда имеем: . Сложив, получим , а так как S a +S b +S c =S, то . Теорема доказана.

Теорема 4: Перпендикуляры, опущенные из точки, лежащей в плоскости треугольника, на его стороны, определяют на сторонах шесть отрезков так, что сумма квадратов трех отрезков, не имеющих общих концов, равна сумме квадратов других трех отрезков (рис. 5).

Дано: треугольник АВС, OL, OM, ON- перпендикуляры, проведенные к сторонам треугольника соответственно.

Доказать: AL 2 + BM 2 + CN 2 = LB 2 + MC 2 + AN 2 .

Доказательство: Так как OL, OM, ON – перпендикуляры, применим теорему Пифагора для соответственных треугольников, получим:

AO 2 — AL 2 = BO 2 — BL 2 , ВО 2 — ВМ 2 = ОС 2 — СМ 2 , ОА 2 — АN 2 = ОС 2 – СN 2 ,

АL 2 — BL 2 = AO 2 — BO 2 , BM 2 – MC 2 = BO 2 – OC 2 , CN 2 – NA 2 = CO 2 — OA 2 .

Сложив последние три равенства, получим:

AL 2 — BL 2 + BM 2 — MC 2 + CN 2 — NA 2 = 0 или

AL 2 + BM 2 + CN 2 = BL 2 + MC 2 + NA 2 . Теорема доказана.

Следующее свойство педального треугольника было открыто Жозефом Нейбергом в 1892 году, в нём рассматриваются педальные треугольники педальных треугольников. Внутренняя точка Р использована для определения треугольника А 1 В 1 С 1 (первого) педального треугольника АВС . Та же самая педальная точка Р снова использовалась для определения педального треугольника А 1 В 1 С 1 , который мы обозначим через А 2 В 2 С 2 и назовем «вторым педальным треугольником» треугольника АВС. Третья операция дает треугольник А 3 В 3 С 3 — педальный треугольник треугольника А 2 В 2 С 2 . И для «третьего педального треугольника» использовалась та же самая точка Р.

Теорема 5: Третий педальный треугольник подобен исходному треугольнику (рис.6)

Доказательство: Соединим точки Р и А. Точка Р принадлежит каждой из окружности, описанной вокруг треугольников АВ 1 С 1 , А 2 В 1 С 2 , А 3 В 3 С 2 , А 2 В 2 С 1 иА 3 В 2 С 3 . Значит углы С 1 АР, С 1 В 1 Р, А 2 В 1 Р, А 2 С 2 Р, В 3 С 2 Р, В 3 А 3 Р равны, а значит и углы РАВ 1 , РС 1 В 1 , РС 1 А 2 , РВ 3 А 2 , РВ 2 С 3 , РА 3 С 3 так же равны.

Другими словами, две части, на которые прямая АР делит угол А, имеют двойников: одна — при вершине В 1 , а другая при вершине С 1 , далее при вершинах С 2 и В 2 и, наконец, обе — при вершине А 3 . Следовательно, треугольник АВС и треугольник А 3 В 3 С 3 имеют равные углы при вершинах А и А 3 . Аналогично, они имеют равные углы В и В 3 . Теорема доказана.

Точкой Брокара называется такая педальная точка, которая при соединении с вершинами треугольника образует равные чередующиеся углы. Такие углы называются углами Брокара [3] .

Решение задач с применением свойств педального треугольника.

Дано: треугольник АВС,

ВС = 8 см, АС = 6 см, АВ = 7 см

треугольник А 1 В 1 С 1 – педальный точки Р,

РА 1 =х=3,5см, РВ 1 =у=5см, РС 1 =z=3,5см,

Найти: стороны педального треугольника.

Решение: Пусть стороны педального треугольника равны а 1 , b 1 и с 1 , тогда согласно теореме 1 имеем:

а 1 = (3,5∙8) : 8 = 3,5 (см), b 1 = (5∙6) : 8 = 3,75 (см), с 1 = (3,5∙7) : 8 = 3 (см).

Ответ: 3,5 см, 3, 75 см, 3 см.

Задача 2. Доказать, что сумма расстояний от любой точки О основания равнобедренного треугольника до его боковых сторон равна высоте этого треугольника, проведенной к боковой стороне.

Дано: треугольник АВС: АВ=АС,

ВН, СН 1 – высоты, точка О є ВС,

ОМ АС, ON АВ, ОМ=х, ON=y.

Доказать: x + y = BH

Доказательство: по теореме 3 , тогда

. Так как ВН=СН 1 (высоты равнобедренного треугольника, проведённые к боковым сторонам), то , ч.т.д.

Задача 3. Доказать, что сумма расстояний от любой точки внутри правильного треугольника до его сторон равна высоте этого треугольника.

Дано: треугольник АВС — правильный,

точка О, x АС, y АВ, z BC, h – высота.

Доказать: x + y+ z = h

Доказательство: по теореме 3 , тогда .

Так как h a = h b = h c (высоты правильного треугольника), то , утверждение доказано.

Задача 4. Стороны треугольника равны 4 см, 13 см, 15 см. Внутри него взята точка Р, которая отстоит от первой стороны на расстоянии 5 см, от второй на 1 см. Найдите расстояние от этой точки до третьей стороны.

Дано: треугольник АВС,

АВ = 4 см, ВС = 13 см, АС = 15 см,

точка Р – внутри треугольника,

АН, ВН, СН – высоты,

РА 1 = 1 см, РС 1 = 5 см,

Решение : Заметим, что треугольник А 1 В 1 С 1 , образованный основаниями перпендикуляров, опущенных из точки Р – педальный. Найдем площадь треугольника АВС по формуле Герона, S = 24 см 2 . Найдем высоты треугольника АВС АН= 48/13 см, СН= 12 см, ВН = 48/15 см.

Тогда по теореме 3 имеем: 13/48 + 5/12 + 15х/48 = 1. Решая это уравнение, получим 15х = 15, х = 1. Значит расстояние от точки Р до третьей стороны треугольника равно 1 см.

Задача 5. Перпендикуляры, опущенные из точки О, взятой внутри треугольника АВС, определяют на сторонах треугольника точки L, M, N так, что , причем . Известно, что АВ = 6, АС = 15. Найдите сторону ВС.

Дано: треугольник АВС, точка О внутри АВС, АВ = 6, АС = 15, ,

Решение: Найдем сначала длины отрезков, на которые разбивают стороны треугольника данные точки. Т.к. АВ = 6, то АL = 1, LB = 5, а АС = 15, то AN = 6, NC = 9. Значит по теореме 4 имеем AL 2 + BM 2 + CN 2 = BL 2 + MC 2 + NA 2 , тогда 1 2 + 4 2 + 9 2 = 5 2 + МС 2 + 6 2 , следовательно МС 2 = 37, МС = . Отсюда ВС = ВМ + МС = .

Данная работа относится к прикладным исследованиям, ее результаты, выраженные с помощью математики, дают возможность познакомиться с интересными, нестандартными вопросами геометрии . В частности, с понятием педального треугольника связаны такие интересные объекты как точка Брокара и прямая Симпсона. В результате проведенной работы мы познакомились с понятием и свойствами педального треугольника, а также показали применение его свойств при решении геометрических задач. Следует отметить, что это позволяет решать сложные математические задачи просто, красиво и понятно.

Таким образом, выдвинутая гипотеза нашла свое подтверждение в данной работе, а все поставленные цели и задачи были успешно выполнены и достигнуты.

Список литературы и Интернет-ресурсов:

Коксетер Г.С., Грейтцер С.Л., Новые встречи с геометрией. – М: Наука, 1978;
Кубышева М.А., Избранные вопросы геометрии.- М, 2006;
Прасолов В.В., Задачи по планиметрии. – М: МЦНМО, 2006;
Прасолов В.В., Точки Брокара. Ж: Квант № 1, 1992, с.42;
Фетисов А.И., Геометрия в задачах. – М: Просвещение, 1977;
Шарыгин И.Ф. Задачи по геометрии. Планиметрия.- М.: Наука, 1986.
Шарыгин И.Ф., Геометрия 7-9 класс. – М: Дрофа, 2006;
http://easymath.com.ua/
http://gigabaza.ru/
http://nsportal.ru/
http://artyomtutor.nsknet.ru/

[1] СИМСОН Роберт (1687—1768)

Шотландский математик, профессор математики в Глазговском университете.

[2] Уоллес Уильям (1768-1843)

Шотландский математик, профессор математики Эдинбургского университета. Исследования относятся к теории конических сечений, теории логарифмов, теории шарнирных механизмов. Доказал теорему о том, что основания перпендикуляров, опушенных на стороны треугольника из точки описанной окружности, лежат на одной прямой. Изобрел пантограф (1831), прибор для копирования рисунков и другие приборы.

[3] БРОКАР Анри (1845-1922)

Французский математик, специалист в области геометрии треугольника и круга. Ряд геометрических образов, связанных с треугольником и кругом, носит в настоящее время имя Брокара (круг, первый и второй треугольники, точки и углы, но только «круг Брокара» принадлежит ему самому). Брокар составил один из наиболее подробных справочников по замечательным кривым.

Предварительный просмотр:

Видео:ПЕДАЛЬНЫЙ треугольникСкачать

Подписи к слайдам:

ФГКОУ Санкт-Петербургское с уворовское военное у чилище Министерства обороны Российской Федерации ПЕДАЛЬНЫЙ ТРЕУГОЛЬНИК Работу выполнил: Неженец Алексей, с уворовец 10 класса 201 5 г.

В ведение Треугольник — одна из основных фигур, изучаемых в геометрии. В школьном курсе геометрии рассматриваются свойства и теоремы о произвольных, равносторонних, равнобедренных, прямоугольных треугольниках. Чтобы расширить представления о треугольниках и их свойствах, познакомимся с педальным треугольником.

Задачи: изучить педальный треугольник; рассмотреть свойства педального треугольника и доказать некоторые из них; рассмотреть задачи с применением свойств педального треугольника.

Объект исследования: педальный треугольник Предмет исследования: свойства педального треугольника

Гипотеза: если выяснить свойства педального треугольника, то возникает объективная возможность для решения задач повышенной сложности.

Пусть Р — любая точка внутри треугольника АВС, и пусть перпендикуляры, опущенные из точки Р на стороны ВС, СА, АВ треугольника, будут РА 1 , РВ 1 и РС 1 . Педальный треугольник — треугольник, вершинами которого являются основания перпендикуляров, опущенных из точки, находящейся внутри треугольника. Сама эта точка называется педальной точкой .

Теорема 1. Если расстояние от педальной точки до вершины треугольника АВС равны х, у, z, то длины сторон педального треугольника равны , где R – радиус описанной окружности . Задача 1. Вычислить стороны педального треугольника, если расстояния от педальной точки до вершин треугольника х=3,5 см, у=5 см, z =3,5 см, R =4 см, а стороны самого треугольника равны соответственно 8 см, 6 см, 7 см.

Y X С D В Z Теорема 2: Основания перпендикуляров, опущенных из точки на стороны треугольника, лежат на одной прямой тогда и только тогда, когда эта точка лежит на описанной окружности. А XZ — прямая Симсона

Теорема 3: Если из точки L внутри треугольника опущены перпендикуляры l a , l b , l c , соответственно на стороны а, b , с треугольника, то Задача 2. Доказать, что сумма расстояний от любой точки основания равнобедренного треугольника до его боковых сторон равна высоте этого треугольника, проведенной к боковой стороне. Задача 3: Стороны треугольника равны 4 см, 13 см, 15 см. Внутри него взята точка Р, которая отстоит от первой стороны на расстоянии 5 см, от второй на 1 см. Найдите расстояние от этой точки до третьей стороны треугольника.

Теорема 4: Перпендикуляры , опущенные из точки, лежащей в плоскости треугольника, на его стороны, определяют на сторонах треугольника шесть отрезков так, что сумма квадратов трех отрезков, не имеющих общих концов, равна сумме квадратов других трех отрезков. Задача 4: Перпендикуляры, опущенные из точки О, взятой внутри треугольника АВС, определяют на сторонах треугольника точки L , M , N так, что ,причем Известно, что АВ = 6, АС = 15. Найдите сторону ВС.

Теорема 5: Третий педальный треугольник подобен исходному треугольнику.

Такая педальная точка, которая при соединении с вершинами треугольника образует равные чередующиеся углы , называется точкой Брокара . Углы называются углами Брокара , например: РАВ = РСА = РВС , т очка Р – точка Брокара

Заключение В результате изучения различных источников и проведенного самостоятельного исследования: узнал, что такое педальный треугольник и как его построить; изучил и доказал несколько свойств педального треугольника; показал применение изученных свойств при решении задач .

Задача 1. Вычислить стороны педального треугольника, если расстояния от педальной точки до вершин треугольника х=3,5 см , у=5 см , z =3,5 см , R =4 см , а стороны самого треугольника равны соответственно 8 см, 6 см, 7 см. Решение: Пусть стороны педального треугольника равны а 1 , b 1 и с 1 , тогда согласно теореме 1 имеем: а 1 = (3,5∙8) : 8 = 3,5 (см), b 1 = (5∙6) : 8 = 3,75 (см), с 1 = (3,5∙7) : 8 = 3 (см). Ответ: 3,5 см, 3, 75 см, 3 см.

y x N M Н 1 Н Задача 2. Доказать, что сумма расстояний от любой точки О основания равнобедренного треугольника до его боковых сторон равна высоте этого треугольника, проведенной к боковой стороне. Доказательство : по теореме 3 , тогда . Так как ВН=СН 1 ч .т.д . А О С В

Задача 3: Стороны треугольника равны 4 см, 13 см, 15 см. Внутри него взята точка Р, которая отстоит от первой стороны на расстоянии 5 см, от второй на 1 см. Найдите расстояние от этой точки до третьей стороны треугольника. Решение : Заметим, что Δ А 1 В 1 С 1 , образованный основаниями перпендикуляров, опущенных из точки Р – педальный. Найдем площадь Δ АВС по формуле Герона, S = 24 см 2 . Найдем высоты Δ АВС: АН=48/13 см, СН=12 см, ВН=48/15 см. Тогда по теореме 3 имеем: 13/48 + 5/12 + 15х/48 = 1. 15х = 15, х = 1. Значит расстояние от точки Р до третьей стороны треугольника равно 1 см. Ответ: 1 см.

Задача 4: Перпендикуляры , опущенные из точки О, взятой внутри треугольника АВС, определяют на сторонах треугольника точки L , M , N так, что , причем . Известно , что АВ = 6, АС = 15. Найдите сторону ВС. Решение: Найдем сначала длины отрезков, на которые разбивают стороны треугольника данные точки. Т.к . АВ = 6 , то А L = 1, LB = 5; а АС = 15, то AN = 6, NC = 9. Значит по теореме 4 имеем AL 2 + BM 2 + CN 2 = BL 2 + MC 2 + NA 2 , тогда 1 2 + 4 2 + 9 2 = 5 2 + МС 2 + 6 2 , следовательно МС 2 = 37, МС = . Отсюда ВС = ВМ + МС = . Ответ:

Видео:Подобие треугольников. Признаки подобия треугольников (часть 1) | МатематикаСкачать

Проект «Педальный треугольник»

Проект по математике «Педальный треугольник» подготовила ученица 8 класса под моим руководством. Цель проекта: применение теорем о педальном треугольнике при решении задач. В работе дается определение педальному треугольнику, доказываются теоремы об этом треугольнике, также рассматриваются точка Брокара, треугольник и окружность Брокара. В практической части показывается как построить педальный треугольник, решаются задачи, в которых применяются теоремы о педальном треугольнике.

Просмотр содержимого документа
«Проект «Педальный треугольник»»

Департамент образования мэрии города Новосибирска

Дворец творчества детей и учащейся молодежи «Юниор»

Городской конкурс исследовательских проектов

учащихся 5-8 классов

Бобылева София Сергеевна

МБОУ ЭКЛ, 8 класс,

Центральный округ г.Новосибирска

Консультант проекта: Кривченкова

учитель математики ВК

Контактный телефон руководителя:

Основная часть 4

Что такое педальный треугольник? 4

Что такое точка Брокара? 4

Треугольник Брокара 5

Окружность Брокара 5

Теоремы о педальном треугольнике 6

Практическая часть 9

Список литературы 15

Искусство решать геометрические задачи

чем-то напоминает трюки иллюзионистов — иногда,

даже зная решение задачи, трудно

понять, как можно было до него додуматься.

Треугольник — первая геометрическая фигура, встречающаяся в древних орнаментах. В Египте он символизировал триаду духовной воли, любви, интуиции и высшего разума человека, то есть его личность или душу.

В герметической идеографии треугольник с устремленной к верху вершиной, символизирует огонь и отвечает идее вознесения, духовности.

Треугольник с горизонтальной чертой считается пассивным и означает воздух, умеренный огонь.

Перевернутый треугольник означает чашу, готовую принять воду; мудрость, порождающую главную идею.

Треугольник – одна из основных фигур, изучаемых в геометрии. В школьной программе рассматриваются несколько видов треугольников, а, чтобы расширить представление об этих необычайно интересных фигурах и их свойствах, мы захотели познакомиться с педальным треугольником. Свойства педального треугольника позволяют решать сложные математические задачи просто, красиво и понятно.

В нашей работе мы собираемся рассмотреть несколько вопросов этого раздела, исходя из этого, мы поставили перед собой следующие цель и задачи.

Цель: применение теорем о педальном треугольнике при решении задач.

Узнать, какой треугольник является педальным.

Изучить его историю.

Разобрать основные теоремы и свойства педального треугольника.

Решить несколько задач по данной теме.

Гипотеза: можно ли сказать, что применение теорем о педальном треугольнике помогает при решении сложных задач.

Методы исследования: сбор информации, обработка данных, сравнение, анализ, обобщение.

Первый этап – теоретический. Поиск и изучение теоретического материала (литературы и Интернет-ресурсов) по теме «Педальный треугольник».

Второй этап – практический. Доказательство теорем и свойств педального треугольника и решение задач с их использованием.

Третий этап – заключительный. Систематизация и обобщение теоретического материала. Анализ решения задач. Формулировка выводов.

Основная часть
Что такое педальный треугольник?

Пусть P любая точка внутри данного треугольника ABC и пусть перпендикуляры, опущенные из точки P на стороны BC, CA, AB треугольника будут P , P и P .

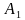
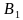
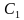
Определение: Треугольник 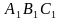, вершинами которого являются основания этих перпендикуляров, называется педальным (подерным) треугольником треугольника ABC для «педальной точки» P.

При торможении автомобиля педаль тормоза бьет обратно в педаль, работая по принципу – точка – тире — точка.

Что такое точка Брокара?

Точкой Брокара называется такая педальная точка, которая при соединении с вершинами треугольника образует равные чередующиеся углы. Такие углы называются углами Брокара.

Т 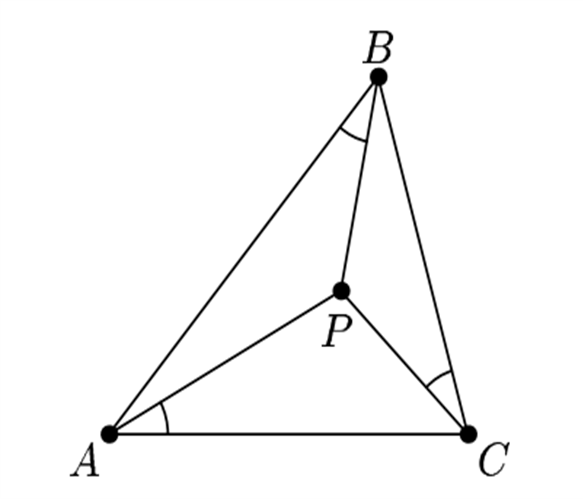очка Брокара — одна из двух точек внутри треугольника, возникающих на пересечении отрезков, соединяющих вершины треугольника с соответствующими свободными вершинами треугольников, подобных данному треугольнику и построенных на его сторонах.

Считаются замечательными точками треугольника, с их помощью строятся многие объекты геометрии треугольника (в том числе, окружность Брокара , треугольник Брокара , окружность Нейберга (см. также Нойберг, Жозеф), окружности Схоуте). Названы в честь французского метеоролога и геометра Анри Брокара, описавшего точки и их построение в 1875 году, однако были известны и ранее, в частности, были построены в одной из работ немецкого математика и архитектора Августа Крелле, изданной в 1816 году.

Брокар Анри (12.05.1845 – 16.02.1922) – французский математик, специалист в области геометрии треугольника и круга. Ряд геометрических образов, связанных с треугольником и кругом, носит в настоящее время имя Брокара (круг, первый и второй треугольники, точки и углы, но только «круг Брокара» принадлежит ему самому). Брокар составил один из наиболее подробных справочников по замечательным кривым. В работе имеются два плаката, формата А3, показывающие расположение точек Брокара внутри треугольника.

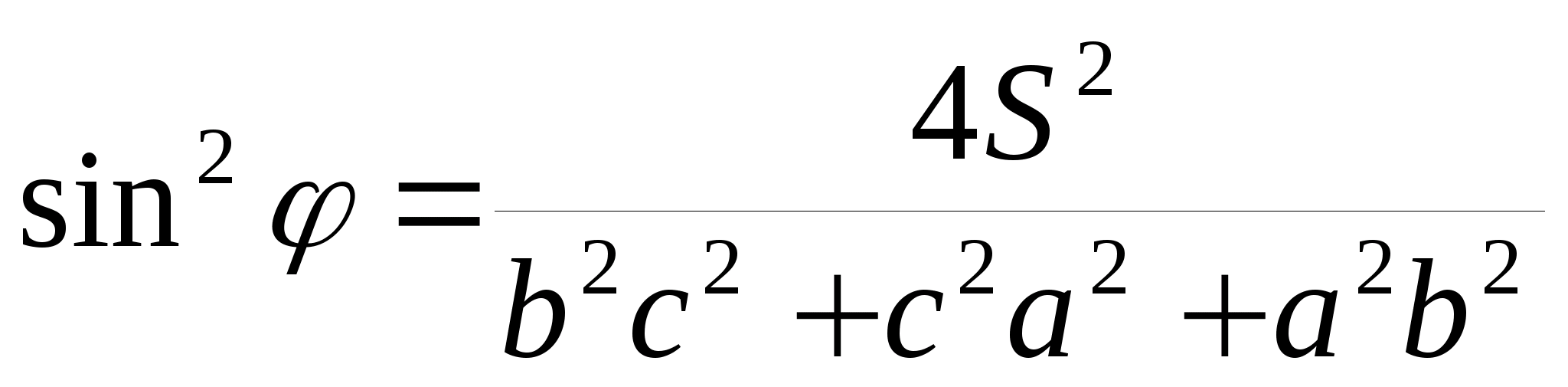
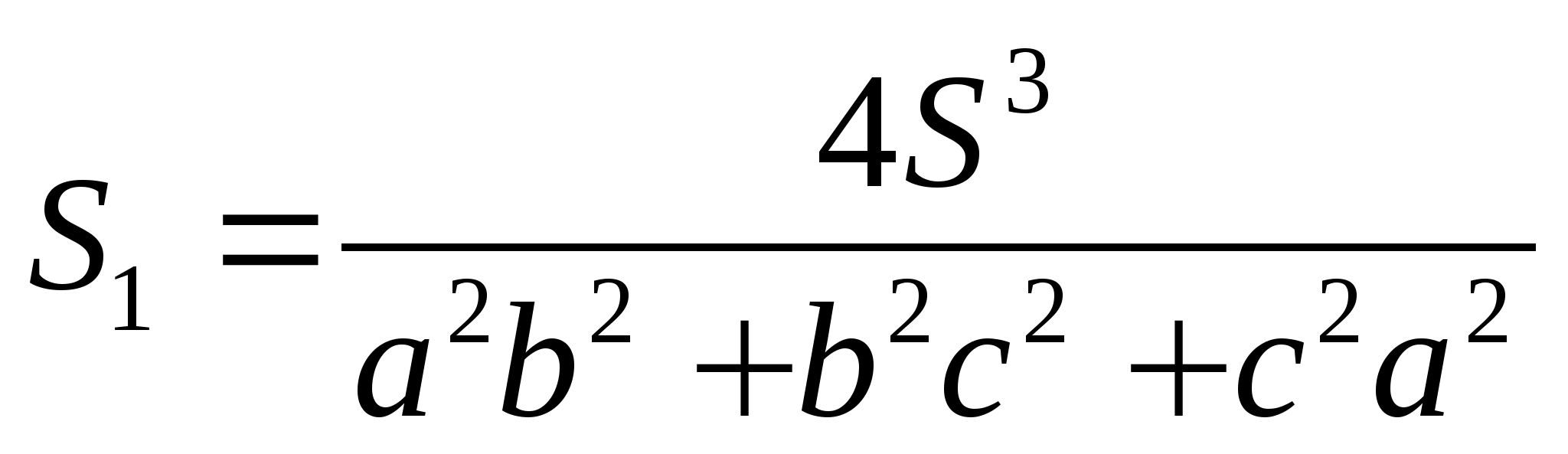
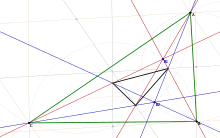
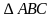
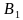
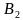
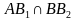
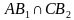
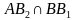
Угол Брокара определяется по формуле , а площадь педального треугольника точки Брокара равна , где S – площадь данного треугольника.

Треугольник Брокара – треугольник, образуемый точками пересечения линий, проведённых из двух различных вершин заданного треугольника через различные точки Брокара: для △ABC и его точек Брокара B1 и B2 вершины одного из треугольников Брокара будут находиться на пересечениях AB1∩BB2 , AB1∩CB2 и AB2∩BB1. Треугольник Брокара вписан в окружность Брокара.

Окружность Брокара (окружность семи точек) — окружность, диаметром которой является отрезок, соединяющий центр описанной окружности данного треугольника и его точку Лемуана. Две точки Брокара лежат на этой окружности, так же, как и три вершины треугольника Брокара. Эта окружность концентрическая с первой окружностью Лемуана.

В равностороннем треугольнике центр описанной окружности и точка Лемуана совпадают, поэтому его окружность Брокара вырождается в точку.

Теоремы о педальном треугольнике

Если точка Брокара Р является пересечением медианы СМ с биссектрисой АЕ, то треугольник правильный.

Видео:8 класс, 22 урок, Первый признак подобия треугольниковСкачать

Презентация: Свойства педального треугольника. Точка Брокара.

Презентация к исследовательской работе на тему: Свойства педального треугольника. Точка Брокара.

Просмотр содержимого документа
«Презентация: Свойства педального треугольника. Точка Брокара.»

Научно-практическая конференция « Свойства педального треугольника. Точка Брокара »

Шаблон для создания презентаций к урокам математики. Савченко Е.М.

Автор работы: Кыржинаков Денис

Обучающийся 9 класса

МБОУ Лестранхозовская СОШ

Научный руководитель: Артемьева

Треугольник — одна из основных фигур, изучаемых в геометрии. В школьном курсе геометрии рассматриваются свойства и теоремы о произвольных, равносторонних, равнобедренных, прямоугольных треугольниках. Чтобы расширить представления о треугольниках и их свойствах, познакомимся с педальным треугольником.

Актуальность темы исследования обусловлена ежегодным усложнением заданий ЕГЭ, что требует углубленных знаний не только в алгебре, но и геометрии.

Шаблон для создания презентаций к урокам математики. Савченко Е.М.

Цели и задачи работы:

Цель: расширить геометрические представления о свойствах треугольника и рассмотреть их практическое применение при решении задач.

Дать общую характеристику треугольнику как геометрической фигуры.
Рассмотреть педальный треугольник как разновидность треугольника, точку Брокара.
Показать практическое применение свойств педального треугольника и расположения точки Брокара.

Шаблон для создания презентаций к урокам математики. Савченко Е.М.

треугольник как геометрическая фигура.

свойства педального треугольника.

если выяснить свойства педального треугольника, месторасположение точки Брокара и овладеть ими, то возникает объективная возможность для решения задач повышенной сложности.

Шаблон для создания презентаций к урокам математики. Савченко Е.М.

Пусть Р — любая точка внутри треугольника АВС, и пусть перпендикуляры, опущенные из точки Р на стороны АВ, ВС, АС треугольника, будут РС 1, РА 1 , и РВ 1 . Педальный треугольник — треугольник, вершинами которого являются основания перпендикуляров, опущенных из точки, находящейся внутри треугольника. Сама эта точка называется педальной точкой .

Шаблон для создания презентаций к урокам математики. Савченко Е.М.

Если при построении педального треугольника углы получаются равными, то они называются углами Брокара , а педальная точка — точкой Брокара .

Шаблон для создания презентаций к урокам математики. Савченко Е.М.

1 0 . Если расстояние от педальной точки до вершины треугольника АВС равны х, у, z , то длины сторон педального треугольника равны где R – радиус описанной окружности.

Шаблон для создания презентаций к урокам математики. Савченко Е.М.