Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.
Развитие управляющих функций мозга ребёнка: полезные советы и упражнения для педагогов
Сертификат и скидка на обучение каждому участнику
Колебания, описываемые уравнением
являются гармоническими, а система, совершающая такие колебания, — гармонической колебательной системой, или гармоническим осциллятором (от лат. oscillo — качаюсь). Его можно получить из второго закона Ньютона max = Fx , где ax = x¨ , а Fx — проекция возвращающей силы, которая зависит от координаты х. Кроме того, уравнение гармонических колебаний можно получить дифференцируя по времени закон сохранения энергия. Ну и наконец, для решения некоторых задач можно воспользоваться готовой формулой для периода колебаний физического маятника:

где m — масса колеблющейся системы, Jz — момент инерции системы относительно оси z вращения, а — расстояние от оси z до центра тяжести [1] системы. Покажем применение всех трёх способов на решении первой задачи.
Задача 1. Выведите формулу Гюйгенса для периода малых колебаний математического маятника в поле тяжести Земли, которую впервые получил ученик И. Ньютона Христиан Гюйгенс.
Рис. 1: закон Ньютона Рис. 2: законы сохранения Рис. 3: физический маятник
1) Колебательная система, состоящая из находящегося в поле силы тяжести тела, подвешенного на лёгкой нерастяжимой нити, размеры которого малы по сравнению с длиной нити, а его масса значительно больше массы нити, называется математическим маятником. При таких условиях тело можно считать материальной точкой, а нить — легкой нерастяжимой ( см. рисунок 1 ). Рассмотрим колебания математического маятника. Отклонение маятника от положения равновесия будем характеризовать углом α ( см. рисунок 1 ), который нить образует с вертикалью. После отклонения маятника на него действуют две силы: направленная вертикально вниз сила тяжести m
g и направленная вдоль нити сила упругости (натяжение T
). Под действием этих сил тело движется по дуге окружности к устойчивому положению равновесия. Согласно второму закону Ньютона для движения маятника, равнодействующая этих сил создаёт центростремительное ускорение, направленное к точке подвеса D:
В проекции на выбранные оси координат Ох и Оу ( см. рисунок 1 ) получаем:
При малых углах отклонения sinα ≈ α и длина дуги AB очень мало отличается от длины хорды AO = lsinα ≈ lα , где угол α выражен в радианах. Тогда смещение маятника вдоль дуги x = lα . Но практически маятник движется вдоль оси Ох. Из треугольника AOD находим:
sinα = 
Таким образом, силой, возвращающей маятник к устойчивому положению равновесия, является сила упругости его нити. При малых углах отклонения маятника проекция вектора ускорения 

где g — ускорение, сообщаемое грузу маятника силой упругости нити. Отсюда получаем уравнение гармонических колебаний математического маятника:
При сравнении последнего последнего уравнения с уравнением гармонического осциллятора, можно сделать вывод, что при малых отклонениях математический маятник совершает гармонические колебания с циклической частотой и периодом:
2) Поскольку при колебаниях гармонического осциллятора силой трения пренебрегают, то его механическая энергия сохраняется. Рассмотрим превращения энергии при колебаниях математического маятника. Выберем систему отсчёта таким образом, чтобы в положении равновесия его потенциальная энергия была равна нулю. При отклонении маятника на угол α ( см. рисунок 2 ), соответствующий максимальному смещению от положения равновесия, потенциальная энергия максимальна, а кинетическая равна нулю (точка А на рисунке 2 ):
Поскольку при прохождении положения равновесия потенциальная энергия равна нулю, то из закона сохранения механической энергии следует, что кинетическая энергия маятника (а следовательно, и скорость) будет максимальна (точка В на рисунке 2 ):
W П max = 0 ,
В положениях между крайними точками полная энергия маятника остаётся постоянной:
Пусть в этом произвольном положении угол отклонения от вертикали равен ϕ . Тогда высота h, отсчитанная от нулевого уровня, может быть выражена через длину l маятника:
При малых углах отклонения, существует приближённое равенство:
Линейная скорость движения груза может быть выражена через угловую:
Тогда полная механическая энергия маятника в произвольный момент времени определится выражением:
Дифференцируем по времени это равенство:
При сравнении последнего последнего уравнения с уравнением гармонического осциллятора, можно сделать вывод, что при малых отклонениях математический маятник совершает гармонические колебания с циклической частотой и периодом:
3) Физическим (или сложным) маятником называется твёрдое тело, вращающееся вокруг горизонтальной оси Oz под действием силы тяжести ( см. рисунок 3 ). Обозначим расстояние ОС центра тяжести маятника от оси вращения через а и силу тяжести через mg, где m — масса маятника. Так как заданной силой является только сила тяжести, то главный момент (сумма моментов всех сил системы) относительно оси Oz равен:
где ϕ — угол отклонения маятника от вертикали, отсчитываемый в направлении, обратном движению часовой стрелки. Как известно из динамики, дифференциальное уравнение вращательного движения твёрдого тела вокруг неподвижной оси имеет вид:
Последнее уравнение представляет дифференциальное уравнение движения физического маятника. При малых углах отклонения маятника приближённо можно принять sinϕ ≈ ϕ . Получим приближённое дифференциальное уравнение малых колебаний маятника:
Общее решение такого уравнения будет являться функция вида:
Постоянные интегрирования C 1 и C 2 зависят от начальных условий: если при t = 0 угол отклонения равен ϕ 0 ( см. рисунок 3 ), то колебания будут происходить по закону косинуса; если при t = 0 угол отклонения равен нулю, то колебания будут происходить по закону синуса. Циклическая частота и период колебаний физического маятника, соответственно будут равны:
Для математического маятника (материальная точка массой m) момент инерции относительно горизонтальной оси Oz равен Jz = ml 2 , а расстояние до центра тяжести a = l. И тогда:
√
Задача 2. Выведите формулу Томсона T = 2π LC для периода в LC-контуре путём дифференцирования закона сохранения.
Задача 3. Однородный цилиндрический поплавок массой m и площадью сечения S плавает вертикально в стакане с водой. Поплавок слегка утопили, а затем отпустили, в результате чего поплавок начал колебаться. Найдите период этих колебаний. Плотность воды ρ , ускорение свободного падения g.
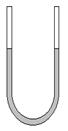
Задача 4. Найдите период малых колебаний жидкости в U-образной трубке постоянного сечения. Длина части сосуда, занятой жидкостью, равна l.
Задача 5. (№ 883: Жилко В.В., Маркович Л.Г. «Сборник задач по физике 10 — 11») Предположим, что сквозь Землю прорыт узкий тоннель от одного её полюса к другому. Пренебрегая сопротивлением воздуха, найдите время полёта τ камня по этому тоннелю от одного полюса Земли до другого. Средний радиус Земли R ⊕ = 6371 км, а ускорение свободного падения на поверхности Земли g = 9,81 м/с 2 .
Задача 6. (МФТИ, 1995 г.) В модели атома Томсона предполагалось, что положительный заряд q, равный по модулю заряду электрона, равномерно распределён внутри шара радиуса R. Чему будет равен период колебаний (внутри шара вдоль диаметра) электрона, помещённого в такой шар? Масса электрона me .
Задача 7. На большой плоской пластине равномерно распределён отрицательный заряд с поверхностной плотностью σ . Однородный стержень массой m и длиной l, по которому равномерно распределён положительный заряд q, вставлен в небольшое отверстие пластины и может двигаться перпендикулярно пластине. Найдите период колебаний стержня. Размеры стержня много меньше размеров пластины. Силы тяжести нет.
Задача 8. (МФТИ, 1995 г.) Определите период малых колебаний в вертикальной плоскости небольшого тела массы m с зарядом q внутри непроводящей сферы радиуса R, если в верхней точке сферы закреплён одноимённый точечный заряд Q. Внутренняя поверхность сферы гладкая. Ускорение свободного падения g.
Задача 9. Бусинка с положительным зарядом q может двигаться без трения по натянутой нити длины 2l, на концах которой закреплены положительные заряды Q (см. рисунок 4). Найдите период малых колебаний бусинки, если её масса равна m.


Рис. 4: к задаче № 9
Рис. 5: к задаче № 10
Рис. 6: к задаче № 11
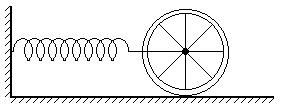
Задача 10. Пружина жёсткости k одним концом присоединена к оси колеса массы m, которое способно катиться без проскальзывания, а другим прикреплена к стенке (см. рисунок 5). Найдите период колебаний системы. Масса колеса однородно распределена по ободу.
Задача 11. (МФТИ, 1996 г.) Конструкция из жёстко соединённых лёгкого стержня и небольшого по размерам шарика массой m может совершать колебания в вертикальной плоскости под действием пружины с жёсткостью k, двигаясь при вращении без трения вокруг горизонтальной оси О (см. рисунок 6). Пружина лёгкая, её точка прикрепления к стержню делит его длину в отношении 1 : 2, считая от шарика. В положении равновесия стержень горизонтален, а ось пружины вертикальна. Найдите: 1) удлинение пружины в положении равновесия системы; 2) период малых колебаний конструкции.
Задача 12. По дну цилиндрической лунки радиусом R катается без проскальзывания полый цилиндр радиусом r (r
Рис. 7: к задаче № 13 Рис. 8: к задаче № 14 Рис. 9: к задаче № 15
Задача 14. (№ 880: Жилко В.В., Маркович Л.Г. «Сборник задач по физике 10 — 11») Найдите период Т колебаний «двойного» математического маятника, изображённого на рисунке 8. Стержень, на котором закреплены грузы массами m 1 и m 2 на расстояниях l 1 и l 2 от оси вращения соответственно, считать невесомым.
Задача 15. (№ 881: Жилко В.В., Маркович Л.Г. «Сборник задач по физике 10 — 11») Вращательный маятник представляет собой однородное колесо массой М и радиусом R с горизонтально расположенной осью, к ободу которого прикреплён груз массой m (см. рисунок 9). Найдите циклическую частоту ω колебаний вращательного маятника в поле тяжести Земли. Трением пренебречь.
Задача 16. (№ 879: Жилко В.В., Маркович Л.Г. «Сборник задач по физике 10 — 11») Маятник Жуковского представляет собой однородный стержень, лежащий на двух быстро вращающихся катках, как показано на рисунке 10. Расстояние между осями катков l = 20 см. Найдите период Т продольных колебаний стержня на катках, если коэффициент трения между стержнем и катками µ = 0,18 .
Рис. 12: к задаче № 18 Рис. 10: к задаче № 16 Рис. 11: к задаче № 17
Задача 17. (№ 4.48: Иродов И.Е.«Задачи по общей физике» 1988 г.) Однородный стержень массы m совершает малые колебания вокруг горизонтальной оси, проходящей через точку О (см. рисунок 11). Правый конец стержня подвешен на невесомой пружине жёсткости k. Найдите период колебаний стержня, если в положении равновесия он горизонтален.
Задача 18. (№ 884: Жилко В.В., Маркович Л.Г. «Сборник задач по физике 10 — 11») «Двойной» пружинный маятник состоит из двух брусков массами m 1 и m 2 , находящихся на гладкой плоскости и соединённых невесомой пружиной жёсткостью k и невесомой нитью (см. рисунок 12). Найдите период Т колебаний маятника, возникших после пережигания нити.
Задача 19. Найдите период колебаний тонкого обруча радиуса R, подвешенного на гвозде. Колебания происходят в плоскости обруча. Проскальзывания нет.
Задача 20. (№ 4.63: Иродов И.Е.«Задачи по общей физике» 1979 г.) Небольшой шарик массы m = 21 г, подвешенный на изолирующей нити на высоте h = 12 см от бесконечной горизонтальной проводящей плоскости, совершает малые колебания (см. рисунок 13). После того как ему сообщили некоторый заряд q, период колебаний изменился в η = 2,0 раза. Найдите заряд q.
Рис. 13: к задаче № 20 Рис. 14: к задаче № 21 Рис. 15: к задаче № 22
Задача 21. (№ 882: Жилко В.В., Маркович Л.Г. «Сборник задач по физике 10 — 11») Механический осциллятор состоит из груза m, пружины жёсткостью k и тонкостенного цилиндрического блока массой М (см. рисунок 14). Считая нить и пружину невесомыми, найдите период Т колебаний груза. Нить по блоку не скользит, трения в оси блока нет.
Задача 22. (№ 4.47: Иродов И.Е.«Задачи по общей физике» 1988 г.) Найдите круговую частоту малых колебаний тонкого однородного стержня массы m и длины l вокруг горизонтальной оси, проходящей через точку О (см. рисунок 15). Жёсткость пружины k, её масса пренебрежимо мала. В положении равновесия стержень вертикален.
Задача 23. (№ 4.48: Иродов И.Е.«Задачи по общей физике» 1979 г.) Физический маятник установили так, что его центр тяжести оказался над точкой подвеса. Из этого положения маятник начал двигаться к положению устойчивого равновесия, которое он прошёл с угловой скоростью ω . Пренебрегая трением, найдите период малых колебаний этого маятника.
Задача 24. (№ 4.52: Иродов И.Е.«Задачи по общей физике» 1979 г.) Тонкая однородная пластинка в форме равностороннего треугольника с высотой h совершает малые колебания вокруг оси, совпадающей с одной из его сторон. Найдите период колебаний и приведённую длину данного маятника.
Задача 23. (МФТИ, 2006 г.) Маятник представляет собой щарнирно прикреплённый к потолку жёсткий лёгкий стержень длины 4l, на котором закреплены два маленьких груза массой m каждый (см. рисунок 16). Трением в шарнире и сопротивлением воздуха можно пренебречь. Найдите: 1) максимальную скорость движения нижнего груза, если стержень отклоняют на угол ϕ 0 = 60 ◦ от вертикали и отпускают без толчка; 2) период колебаний маятника при малых отклонениях от положения равновесия.

Рис. 16: к задаче № 23 Рис. 17: к задаче № 24
Рис. 18: к задаче № 25
Задача 24. (МФТИ, 1996 г.) Груз массой m подвешен с помощью пружины жёсткостью k, лёгких нитей и невесомого блока (см. рисунок 17). Найдите: 1) удлинение пружины в положении равновесия системы; 2) период вертикальных колебаний груза при условии непровисания нитей.
Задача 25. (МФТИ, 1996 г.) Металлический прут в форме дуги окружности радиусом R висит на двух лёгких нитях длины R каждая (см. рисунок 18). Масса прута равна m, его поперечное сечение постоянно. Угол между нитями равен 2ϕ . Найдите: 1) силу натяжения нитей в положении равновесия; 2) период малых колебаний такой «дуги» в вертикальной плоскости, совпадающей с плоскостью «дуги».
[1] Точнее было бы говорить о центре масс (центре инерции системы). Но в том случае, когда система твёрдых тел находится в однородном поле силы тяжести, центр масс и центр тяжести совпадают.
Видео:Определение центра дуги окружности, построение окружности по 3 точкамСкачать

Задача 1 Задача 2 Задача 3 Задача 4
Задача 1 — Жестко соединенная конструкция из легкого стержня и небольшого по размерам шарика массой m может совершать колебания в вертикальной плоскости под действием пружины k, двигаясь при вращении без трения вокруг горизонтальной оси О. Пружина легкая, точка прикрепления ее к стержню делит его длину в отношении 1:2, считая от шарика. В положении равновесия шарик горизонтален, а ось пружины вертикальна. Найдите удлинение пружины в положении равновесия системы. Найдите период малых колебаний конструкции.
Задача 2 — Жестко соединенная конструкция из легкого стержня и небольшого по размерам шарика массой m может совершать колебания под действием двух пружин жесткостью k1 и k2, двигаясь при вращении без трения вокруг вертикальной оси О по гладкой поверхности стола. Пружины легкие, их оси горизонтальны, а точки прикрепления их к стержню делят его на три равные части. В положении равновесия оси пружин перпендикулярны
стержню, и пружина жесткостью k1 растянута на величину L1. Найдите деформацию второй пружины в положении равновесия. Найдите период малых колебаний конструкции.
Задача 3 — Металлический прут в форме дуги окружности радиусом L висит на двух легких нитях длиной L каждая. Масса прута равна m, его поперечное сечение постоянно. Угол между нитями 2b. Найдите силу натяжения нитей в положении равновесия. Найдите период малых колебаний такой «дуги» в вертикальной плоскости, совпадающей с плоскостью «дуги».
Задача 4 — Как изменится частота колебаний математического маятника, представляющего собой груз на легкой пружине, если к середине стрежня прикрепить горизонтальную пружину жесткости k?
Дифференцируем закон сохранения механической энергии
Задача 1 — Получите дифференциальное уравнение гармонических колебаний для уже исследованных и знакомых Вам колебательных систем: горизонтального и вертикального пружинногомаятников, математического маятника. Убедитесь в том, что в рассматриваемых ситуациях это равноценный математический прием.
Задача 2 — Пружина жесткостью k одним концом присоединена к оси колеса массы m, которое способно катиться без проскальзывания, а другим концом присоединена к стенке. Какова частота колебаний системы? Масса колеса однородно распределена по ободу.
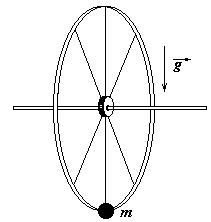 |
Задача 3 — К ободу колеса с горизонтально расположенной осью прикрепили грузик массы m. Найдите массу колеса, предполагая ее однородно распределенной по ободу, если частота малых колебаний колеса с грузиком вокруг оси равна W, а его радиус равен R. (МГУ)
Задача 4 — Найдите частоту колебаний тонкого обруча радиуса R, подвешенного на гвозде. Проскальзывания нет; колебания происходят в плоскости обруча.
Колебательные системы
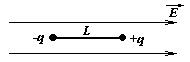 |  |
1 Жесткий диполь, длина которого L и концевые заряды q, помещен в однородное электрическое поле напряженностью Е. Определите период малых колебаний диполя в электрическом поле. Масса каждого из концевых зарядов m.
2 Бусинка массой m с зарядом q может двигаться без трения по натянутой нити длины 2L, на концах которой закреплены заряды Q. Найдите период малых колебаний бусинки относительно положения равновесия.
3 В модели атома Томсона предполагалось, что положительный заряд q, равный по модулю заряду электрона, равномерно распределен внутри шара радиусом R. Чему равен период колебаний (внутри шара, вдоль его диаметра) электрона, помещенного в такой шар? Масса электрона m.
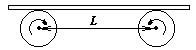 |
4 Доска массы m лежит на двух катках, вращающихся с большой угловой скоростью навстречу друг другу. Расстояние между осями катков L, коэффициент трения скольжения доски по катку m. Найдите частоту продольных колебаний доски.
5 Определите период малых колебаний ртути массы m = 200 г, налитой в U-образную трубку сечения S = 0,50 см 2 . Плотность ртути r = 13,6×10 кг/м 3 .
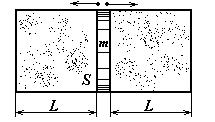
6 Найдите период малых колебаний поршня массы m, разделяющего гладкий горизонтальный цилиндрический сосуд сечения S на две части длины L каждая. По обе стороны поршня находится га при давлении p0 и температуре Т0. При колебании поршня температура газа не меняется.
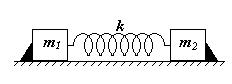
7 Два грузика, скрепленные пружиной жесткости k, находятся на гладкой горизонтальной поверхности. Пружину сжимают и удерживают в деформированном состоянии двумя упорами. Упоры убирают.. Найдите период колебаний, которые возникнут в системе.
 |
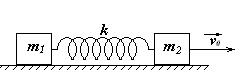 |
8 Два грузика, скрепленные пружиной жесткости k, находятся на гладкой горизонтальной поверхности. Пружина не деформирована. Толчком одному из грузов сообщают скорость v0. Опишите дальнейшее поведение системы. Найдите максимальную деформацию пружины.
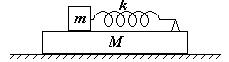 |
9 Тело массы m скреплено пружиной жесткости k с бруском массы M. Пружину сжимают, удерживая тела в неподвижном состоянии, а затем освобождают. Определите периоды колебаний Т1 и Т2 тела и бруска.
10 На гладкой горизонтальной поверхности находится тележка массы М с установленным на ней математическим маятником длины L и массы m. Найдите период колебаний системы.
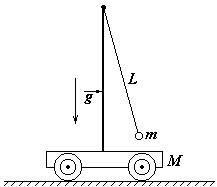 |
11 Найдите отношение частот колебаний молекулы Н2 и молекулы НD (D – атом дейтерия).
12 В системе из задачи 1 убирают один из упоров (допустим, правый). Как будет зависеть от времени величина деформации пружины? Начальная деформация пружины DL.
Видео:Длина дуги окружности. 9 класс.Скачать

Задачи для самостоятельного решения
Читайте также:
|
 |
На горизонтальной пружине укреплено тело массы М = 10 кг, лежащее на абсолютно гладком столе. В это тело попадает и застревает в нем пуля массы m = 10 г, летящая со скоростью v = 500 м/с, направленной вдоль оси пружины. Амплитуда возникших при этом колебаний А = 0,1 м. Определите период возникших колебаний Т.
2. К одному концу первоначально недеформированной и неподвижной пружины жесткости k прикреплен груз массы m. Свободный конец пружины стали тянуть с постоянной скоростью, как показано на рисунке, пока он не переместился на расстояние d. Затем его резко остановили. При какой скорости этого конца пружины груз после остановки не будет колебаться?
 |
3. Чашка пружинных весов массы m совершает гармонические колебания с амплитудой А. В некоторый момент времени на нее положили (без начальной скорости) груз массой М. В результате колебания прекратились. Определите первоначальный период колебаний Т.
4. Точку подвеса математического маятника длины L мгновенно приводят в движение в горизонтальном направлении с постоянной скоростью v, затем, после того, как она переместилась на расстояние S, мгновенно останавливают. При каком значении скорости v колебания маятника, возникшие с началом движения, прекратятся сразу же после остановки? Перед началом движения маятник покоился. Колебания маятника считать малыми.
5. Горизонтальная подставка совершает в вертикальном направлении гармонические колебания с амплитудой А. Какой должна быть циклическая частота w этих колебаний, чтобы лежащий на подставке предмет не отделялся от нее?
6. Одна из обкладок незаряженного плоского конденсатора площади S подвешена на пружине, вторая обкладка закреплена неподвижно. Расстояние между пластинами в начальный момент равно L0. Конденсатор на короткое время подключили к батарее, и он зарядился до напряжения U. Какой должна быть жесткость пружины k, чтобы не произошло качания пластин в результате их взаимного притяжения после зарядки?
7. К одному концу первоначально недеформированной и неподвижной пружины жесткости k прикреплен груз массы m. Свободный конец пружины стали тянуть с постоянной скоростью, как показано на рисунке, пока он не переместился на расстояние d. Затем его резко остановили. При какой скорости этого конца пружины груз после остановки не будет колебаться?
Составьте дифференциальное уравнение гармонических колебаний и определите период колебаний следующих колебательных систем.
1. 
Используем второй закон динамики Ньютона (для поступательного движения). Помним, что координата груза (отсчитываемая, кстати, от положения равновесия) не всегда равна удлинению пружины!!
Задача 1 Задача 2 Задача 3* Задача 4** Задача 5**
Задача 1 — очень просто! Не забудьте, что в процессе движения на груз действует не только пружина. В положении равновесия пружина деформирована, значит, координата груза и величина деформации пружины численно не совпадают.
Задача 2 — после первой задачи разобраться в этой ситуации не сложно. Действуем так же.
Задача 3 – (МФТИ) -казалось бы, что изменилось в сравнении с первой ситуацией! Пружина и нерастяжимый трос по-прежнему невесомы. Просто добавился невесомый блок. Физика существенно изменилась!
Вспомните не только кинематические, но и динамические связи!
Задача 4 – (МГУ) – пружин стало две, а нить по-прежнему невесома. Подумайте, как соединены между собой пружины, каковы силы упругости, возникшие в них. Ну и, конечно, не забудьте кинематические и динамические связи.
Задача 5 — несколько лет назад эта задача предлагалась на окружной олимпиаде. Конечно, не просто не забыть обо всем…
2.
 |  |  |
Используем второй закон динамики вращательного движения.
 |
Задача 1 Задача 2 Задача 3 Задача 4
Задача 1. Жестко соединенная конструкция из легкого стержня и небольшого по размерам шарика массой m может совершать колебания в вертикальной плоскости под действием пружины k, двигаясь при вращении без трения вокруг горизонтальной оси О. Пружина легкая, точка прикрепления ее к стержню делит его длину в отношении 1:2, считая от шарика. В положении равновесия шарик горизонтален, а ось пружины вертикальна. Найдите удлинение пружины в положении равновесия системы. Найдите период малых колебаний конструкции.
Задача 2. Жестко соединенная конструкция из легкого стержня и небольшого по размерам шарика массой m может совершать колебания под действием двух пружин жесткостью k1 и k2, двигаясь при вращении без трения вокруг вертикальной оси О по гладкой поверхности стола. Пружины легкие, их оси горизонтальны, а точки прикрепления их к стержню делят его на три равные части. В положении равновесия оси пружин перпендикулярны стержню, и пружина жесткостью k1 растянута на величину L1. Найдите деформацию второй пружины в положении равновесия. Найдите период малых колебаний конструкции.
Задача3. Металлический прут в форме дуги окружности радиусом L висит на двух легких нитях длиной L каждая. Масса прута равна m, его поперечное сечение постоянно. Угол между нитями 2b. Найдите силу натяжения нитей в положении равновесия. Найдите период малых колебаний такой «дуги» в вертикальной плоскости, совпадающей с плоскостью «дуги».
Задача 4. Как изменится частота колебаний математического маятника, представляющего собой груз на легкой пружине, если к середине стрежня прикрепить горизонтальную пружину жесткости k?
3. Дифференцируем закон сохранения механической энергии.
Для начала получите дифференциальное уравнение гармонических колебаний для уже исследованных и знакомых Вам колебательных систем: горизонтального и вертикального пружинногомаятников, математического маятника. Убедитесь в том, что в рассматриваемых ситуациях это равноценный математический прием.
 |
Задача 1. Пружина жесткостью k одним концом присоединена к оси колеса массы m, которое способно катиться без проскальзывания, а другим концом присоединена к стенке. Какова частота колебаний системы? Масса колеса однородно распределена по ободу.
 |
Задача 2. К ободу колеса с горизонтально расположенной осью прикрепили грузик массы m. Найдите массу колеса, предполагая ее однородно распределенной по ободу, если частота малых колебаний колеса с грузиком вокруг оси равна W, а его радиус равен R. (МГУ)
Задача 3. Найдите частоту колебаний тонкого обруча радиуса R, подвешенного на гвозде. Проскальзывания нет; колебания происходят в плоскости обруча.
Колебательные системы
1.
 |  |
Жесткий диполь, длина которого L и концевые заряды q, помещен в однородное электрическое поле напряженностью Е. Определите период малых колебаний диполя в электрическом поле. Масса каждого из концевых зарядов m.
2. Бусинка массой m с зарядом q может двигаться без трения по натянутой нити длины 2L, на концах которой закреплены заряды Q. Найдите период малых колебаний бусинки относительно положения равновесия.
3. В модели атома Томсона предполагалось, что положительный заряд q, равный по модулю заряду электрона, равномерно распределен внутри шара радиусом R. Чему равен период колебаний (внутри шара, вдоль его диаметра) электрона, помещенного в такой шар? Масса электрона m.
4.
 |  |
Доска массы m лежит на двух катках, вращающихся с большой угловой скоростью навстречу друг другу. Расстояние между осями катков L, коэффициент трения скольжения доски по катку m. Найдите частоту продольных колебаний доски.
5. Определите период малых колебаний ртути массы m = 200 г, налитой в U-образную трубку сечения S = 0,50 см 2 . Плотность ртути r = 13,6×10 кг/м 3 .
6.
 |
Найдите период малых колебаний поршня массы m, разделяющего гладкий горизонтальный цилиндрический сосуд сечения S на две части длины L каждая. По обе стороны поршня находится га при давлении p0 и температуре Т0. При колебании поршня температура газа не меняется.
Колебательные системы – 2
1.
 |
Два грузика, скрепленные пружиной жесткости k, находятся на гладкой горизонтальной поверхности. Пружину сжимают и удерживают в деформированном состоянии двумя упорами. Упоры убирают.. Найдите период колебаний, которые возникнут в системе.
2.
 |
Два грузика, скрепленные пружиной жесткости k, находятся на гладкой горизонтальной поверхности. Пружина не деформирована. Толчком одному из грузов сообщают скорость v0. Опишите дальнейшее поведение системы. Найдите максимальную деформацию пружины.
3.
 |
Тело массы m скреплено пружиной жесткости k с бруском массы M. Пружину сжимают, удерживая тела в неподвижном состоянии, а затем освобождают. Определите периоды колебаний Т1 и Т2 тела и бруска.
4.
 |
На гладкой горизонтальной поверхности находится тележка массы М с установленным на ней математическим маятником длины L и массы m. Найдите период колебаний системы.
5. Найдите отношение частот колебаний молекулы Н2 и молекулы НD (D – атом дейтерия).
6. В системе из задачи 1 убирают один из упоров (допустим, правый). Как будет зависеть от времени величина деформации пружины? Начальная деформация пружины DL.
 |
Дата добавления: 2015-07-24 ; просмотров: 923 | Нарушение авторских прав
🎬 Видео
8 класс, 33 урок, Градусная мера дуги окружностиСкачать

Как правильно гнуть трубу Борьба с бракомСкачать

Длина дуги окружности. Практическая часть. 9 класс.Скачать
Котика ударило током, 10 т. ВольтСкачать

Фермы больше не нужны! Тестируем дуги из профильной трубы / Результат удивил!Скачать

Расчет сегмента окружности по хорде и длине цилиндрической поверхности (трансцендентное уравнение)Скачать

ПРОЩЕ НЕ ПРИДУМАЛИ # НЕ ПРОПУСТИ! ПРИГОДИТСЯ! Холодная ковка из ПРОФИЛЬНОЙ ТРУБЫ.Скачать

КОЛЬЦЕГИБ.Как согнуть кольцо любого диаметра из арматуры, без хитроумных приспособлений за 2 минуты.Скачать

Как Согнуть ПРУТОК или КВАДРАТ в кольцо ЗА 30 СЕКУНД!Скачать

ДЛИНА ДУГИ окружности 9 класс Атанасян 1111 1112 длина окружностиСкачать

Урок 44. Вращение твердого тела. Линейная и угловая скорость. Период и частота вращения.Скачать

Криволинейное, равномерное движение материальной точки по окружности. 9 класс.Скачать

ДУГИ для ПАРНИКА какие лучше? Опыт 15 летСкачать

Параметризация длины дуги окружностиСкачать

Как правильно согнуть трубу под теплицу.Скачать

Геометрия 8 класс (Урок№26 - Градусная мера дуги окружности. Центральные углы.)Скачать

Сегмент окружности - как найти площадь фермы для кровли.Скачать

Окружнось. Зависимость длины хорды, от длины дуги.Скачать