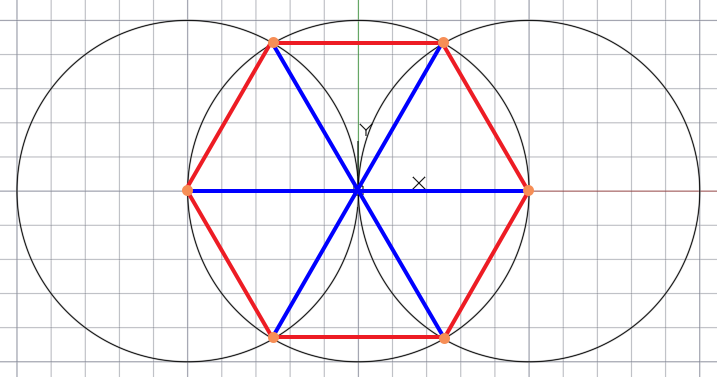
Как разметить круг на 6 равных частей по окружности (4 видео)

Деление окружности на 6 равных частей

Итак, разделим окружность на шесть равных частей с использованием циркуля. Чертим окружность циркулем.

По оси X — по горизонтали (или по оси Y — по вертикали) проводим отрезок — диаметр окружности в виде развёрнутого угла 180 0 .

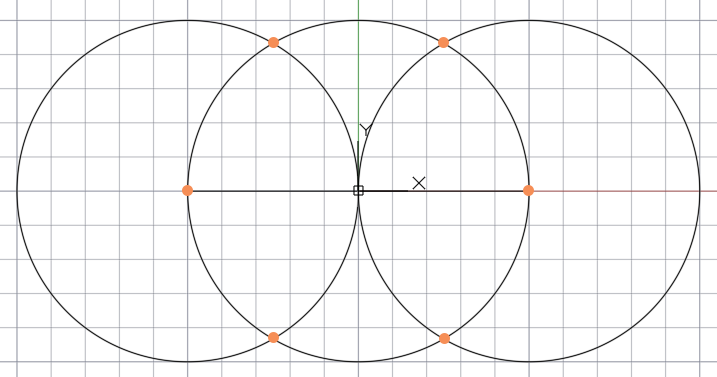
В точках пересечения диаметра с полуосями отмечаем точки, которые являются центрами дополнительных двух окружностей. Чертим окружности.

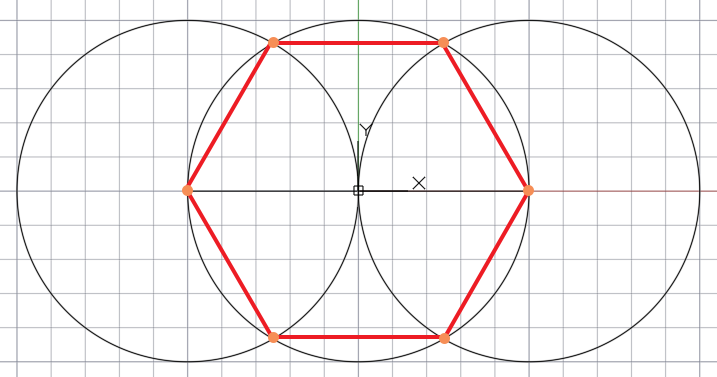
Точки пересечения дуг дополнительных окружностей с основной окружностей и точек их центров последовательно соединяем друг с другом в результате получаем правильный шестиугольник.

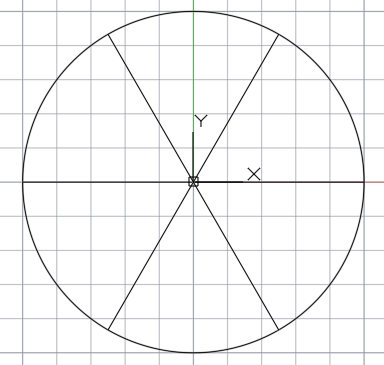
Потом соединяем вершины шестиугольника с центом основной окружности и получаем окружность с 6 равными частями

Окружность, разделённая на 6 равных частей

Содержание

Деление окружности на любое число равных частей
Термины при построениях окружности
Деление окружности на 4 и 8 одинаковых частей
Деление окружности на 3 и 6 равных частей (кратные 3 трём)
Деление окружности на 5 и 10 равных частей
Деление окружности на N-ное количество одинаковых частей (построение правильного многоугольника с N сторон)
Нахождение центра дуги окружности
Как разделить окружность на 6 частей
🎦 Видео

Видео:Как разделить окружность на 6 частей. How to divide a circle into 6 partsСкачать

Деление окружности на любое число равных частей

Как разделить окружность на заданное количество одинаковых частей, терминология при построении окружности, деление окружности на 3, 4, 5, 6, 8, 10 частей.

Термины при построениях окружности

Окружностью называется замкнутая кривая линия, каждая точка которой расположена на одинаковом расстоянии от одной точки О, называемой центром.

Прямые линии, соединяющие любую точку окружности с её центром, называют радиусами R.

Прямая АВ, соединяющая две точки окружности и проходящая через её центр О, называется диаметром D.

Части окружностей называются дугами.

Прямая СD, соединяющая две точки на окружности, называется хордой.

Прямая МN,которая имеет только одну общую точку с окружностью называется касательной.

Часть круга, ограниченная хордой СD и дугой, называется сигментом.

Часть круга, ограниченная двумя радиусами и дугой, называется сектором.

Две взаимно перпендикулярные горизонтальная и вертикальная линии, пересекающиеся в центре окружности, называются осями окружности.

Угол, образованный двумя радиусами КОА, называется центральным углом.

Два взаимно перпендикулярных радиуса составляют угол в 90 0 и ограничивают 1/4 окружности.

Видео:Деление окружности на 6 равных частейСкачать

Деление окружности на 4 и 8 одинаковых частей

Проводим окружность с горизонтальной и вертикальной осями, которые делят её на 4-ре равные части. Проведённые с помощью циркуля или угольника под 45 0 , две взаимно перпендикулярные линии делят окружность на 8-мь равных частей.

Видео:Деление окружности на 3; 6; 12 равных частейСкачать

Деление окружности на 3 и 6 равных частей (кратные 3 трём)

Для деления окружности на 3, 6 и кратное им количество частей, проводим окружность заданного радиуса и соответствующие оси. Деление можно начинать от точки пересечения горизонтальной или вертикальной оси с окружностью. Заданный радиус окружности последовательно откладывается 6-ть раз. Затем полученные точки на окружности последовательно соединяются прямыми линиями и образуют правильный вписанный шести-угольник. Соединение точек через одну даёт равносторонний треугольник, и деление окружности на три равные части.

Видео:Как разделить окружность на 6 частейСкачать

Деление окружности на 5 и 10 равных частей

Построение правильного пятиугольника выполняется следующим образом. Проводим две взаимно перпендикулярные оси окружности равные диаметру окружности. Делим правую половину горизонтального диаметра пополам с помощью дуги R1. Из полученной точки «а» в середине этого отрезка радиусом R2 проводим дугу окружности до пересечения с горизонтальным диаметром в точке «b». Радиусом R3 из точки «1» проводят дугу окружности до пересечения с заданной окружностью (т.5) и получают сторону правильного пятиугольника. Расстояние «b-О» даёт сторону правильного десятиугольника.

Деление окружности на N-ное количество одинаковых частей (построение правильного многоугольника с N сторон)

Выполняется следующим образом. Проводим горизонтальную и вертикальную взаимно перпендикулярные оси окружности. Из верхней точки «1» окружности проводим под произвольным углом к вертикальной оси прямую линию. На ней откладываем равные отрезки произвольной длины, число которых равно числу частей на которое мы делим данную окружность, например 9. Конец последнего отрезка соединяем с нижней точкой вертикального диаметра. Проводим линии, параллельные полученной, из концов отложенных отрезков до пересечения с вертикальным диаметром, разделив таким образом вертикальный диаметр данной окружности на заданное количество частей. Радиусом равным диаметру окружности, из нижней точки вертикальной оси проводим дугу MN до пересечения с продолжением горизонтальной оси окружности. Из точек M и N проводим лучи через чётные ( или нечётные) точки деления вертикального диаметра до пересечения с окружностью. Полученные отрезки окружности будут являться искомыми, т.к. точки 1, 2, …. 9 делят окружность на 9-ть ( N ) равных частей.

Видео:Как разделить круг на равные частиСкачать

Нахождение центра дуги окружности

Для нахождения центра дуги окружности нужно выполнить следующие построения: на данной дуге отмечаем четыре произвольные точки А, В, С, D и соединяем их попарно хордами АВ и СD. Каждую из хорд при помощи циркуля делим пополам, получив, таким образом, перпендикуляр, проходящий через середину соответствующей хорды. Взаимное пересечение этих перпендикуляров даёт центр данной дуги и соответствующей ей окружности.

Видео:Деление окружности на равные части. Урок 6. (Часть 1. ГЕОМЕТРИЧЕСКИЕ ПОСТРОЕНИЯ)Скачать

Как разделить окружность на 6 частей

Автор: Джули · Опубликовано 06.12.2012 · Обновлено 26.10.2016

Иногда для изготовления трафаретов, шаблонов, рисунков, выкроек, поделок необходимо разделить окружность на 6 частей.
Например, здесь нам потребовалось изготовить шаблон для цветка в виде шестиконечной звезды.

Для тех, кто забыл геометрию, напоминаю, что разделить окружность на 6 частей можно двумя способами:

С помощью транспортира.
С помощью циркуля.

1. Как разделить окружность на 6 частей с помощью транспортира

Разделить окружность с помощью транспортира очень просто.

Проводим линию, соединяющую центр и любую точку (например, точку 1) на окружности. От этой линии с помощью транспортира откладываем угол 60, 120, 180 градусов. Ставим на окружности точки (например, точки 2, 3, 4) Разворачиваем транспортир и делим другую часть окружности таким же способом.

2. Как разделить окружность на 6 частей с помощью циркуля

Бывает, что под рукой нет транспортира. Тогда окружность можно разделить на 6 равных частей с помощью циркуля.

Чертим окружность, например, радиусом 5 см. (окружность красного цвета). Не изменяя радиуса, переносим ножку циркуля на окружность (точка 1) и чертим еще одну окружность. Получаем две точки пересечения черной и красной окружностей 6 и 2.

Переносим ножку циркуля в точку 2 и опять проводим окружность. Получаем точку 3.

Переносим ножку циркуля в точку 3. Опять чертим окружность.

Таким образом, продолжаем делить окружность, пока не разделим ее на 6 равных частей.