Моменты инерции относительно осей Оx, Оx1, Оy, Оy1:
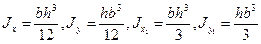
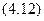
моменты инерции относительно осей Оx, О1x1 и О2x2,:
Прямоугольный и равнобедренный треугольники.
Для прямоугольного треугольника определим центробежный момент инерции Jxy относительно центральных осей Ox и Oy, параллельных катетам:
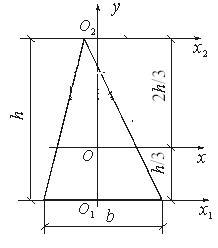
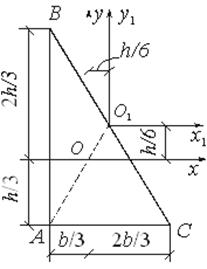
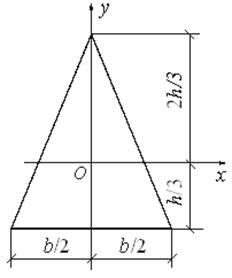
Момент инерции равнобедренного треугольника относительно оси
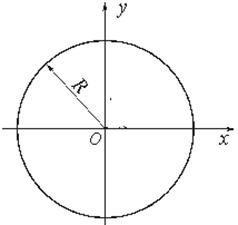
Круг. Полярный момент инерции круга:
Учитывая, что для круга Jx = Jy и полярный момент согласно равен сумме двух осевых моментов, получим:
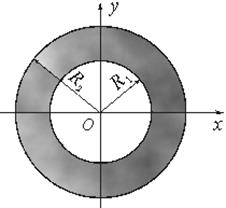
Кольцевое сечение. Моменты инерции кольца находятся как разность моментов инерции двух кругов с радиусами R2 и R1 :
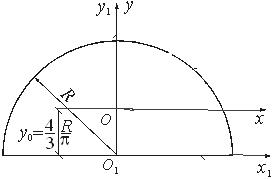
Относительно осей O1x1 и O1y1, которые являются главными осями для полукруга, осевые моменты инерции равны половине момента инерции круга:
Момент инерции относительно главной центральной оси определяется с помощью первой формулы:
Геометрические характеристики сечений прокатных профилей (двутавры, швеллеры, уголки) приведены в таблицах сортамента прокатной стали.
Моменты инерции составных сечений. При определении моментов инерции составного сечения последнее разбивают на простые фигуры, у которых известны положения центров тяжести и моменты инерции относительно собственных центральных осей. По формулам (4.6) находят координаты центра тяжести всего сечения в системе произвольно выбранных вспомогательных осей. Параллельно этим осям проводят центральные оси, относительно которых определяют осевые и центробежный моменты инерции по формулам (4.7). Моменты инерции относительно главных центральных осей определяются по формуле (4.11), а положение главных центральных осей – по формулам (4.10).
Далее рассмотрены примеры задач.
5. Примеры решения задач
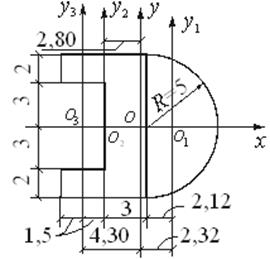
Пример 1. Определим положение центра тяжести и моменты инерции относительно главных центральных осей сечения, состоящего из полукруга и прямоугольника с вырезом. Размеры сечения на рисунке даны в сантиметрах.
Разобьем сечение на три простые фигуры: полукруг с радиусом R=5 см, прямоугольник с размерами сторон 6×10 см, прямоугольный вырез с размерами 3×6 см и определим площади и моменты инерции этих фигур относительно собственных центральных осей.
Для полукруга по формулам (2.21) и (2.22) имеем:
Положение центра тяжести О1 полукруга определяется по формуле (2.20) и равно 0,424·5 = 2,12 см (рис.2.15).
Для прямоугольника и прямоугольного выреза по формулам (2.13) получим
Площадь всего сечения равна F = 39,2 + 60 – 18 = 81,2 см 2 .
Центр тяжести О сечения лежит на горизонтальной оси симметрии. Для определения его положения выберем в качестве вспомогательной оси центральную ось прямоугольника O2y2 . Тогда получим
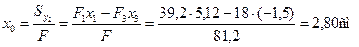
Отложим эту величину от оси О2y2 вправо и проведем ось Оy, которая вместе с осью Ох составит пару главных центральных осей всего сечения. Определим координаты центров тяжести отдельных фигур в системе координат Оxy: а1 = 2,32 см, а2 = – 2,80 см, а3 = – 4,30 см .
По формулам (2.6) найдем моменты инерции сечения относительно осей Ох и Оy:
Пример 2.Для стержня несимметричного сечения, составленного из швеллера [ 30 и неравнобокого уголка L180х110х12, определим центр тяжести сечения, моменты инерции относительно главных центральных осей и положение этих осей. На рисунке размеры даны в сантиметрах.
Выпишем геометрические характеристики сечения швеллера:
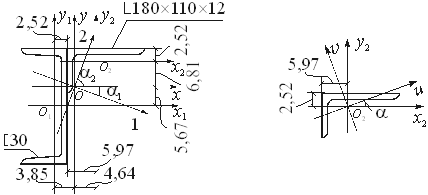
Геометрические характеристики сечения неравнобокого уголка:
Величину центробежного момента инерции уголка 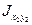
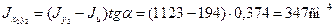
где tga = 0,374 – тангенс угла наклона главной оси u к оси Ох2 , величина которого приведена в сортаменте.
Площадь всего сечения равна F = 40,5 + 33,7 = 74,2 см 2 .
Для определения положения центра тяжести выберем в качестве вспомогательных осей оси швеллера О1x1 и О1y1. Тогда по формулам (2.5) получим
Эти величины и координаты центров тяжести швеллера и уголка в системе координат Охy показаны на рисунке и соответственно равны:
Определим по формулам (2.6) моменты инерции сечения относительно центральных осей Ох и Оy.
По формулам (2.12) и (2.11) найдем величины главных моментов инерции и углы наклона главных осей 1 и 2 к оси Ох :
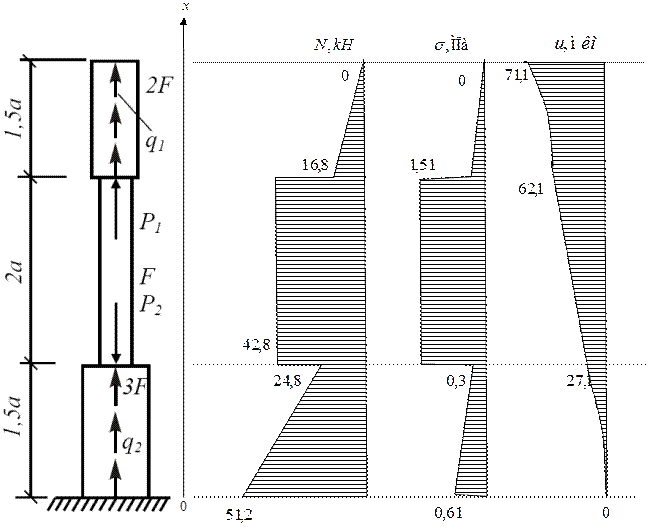
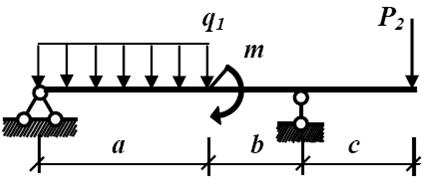
Пример 3. Для статически определимого стержня ступенчато постоянного сечения при заданных осевых нагрузках и геометрических размерах по строке требуется:
1.Определить опорную реакцию в месте закрепления стержня.
2.Вычислить значения продольных сил и нормальных напряжений в характерных сечениях и построить эпюры этих величин.
3.Найти величины абсолютных удлинений (укорочений) участков стержня и величину общего удлинения (укорочения) стержня в целом.
4.Определить значения осевых перемещений характерных сечений и построить эпюру осевых перемещений.
| a, м | F, см 2 | Р1, кН | Р2, кН | q1, кН/м | q2, кН/м | Е, МПа |
| 0,8 | 2,0·10 5 |
1. Составим уравнение равновесия:
2. Вычислим значения продольных сил:
Участок 1:
При 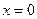
При 
Значение продольной силы линейно уменьшается
Участок 2:
При 
При 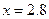
Значение продольной силы не изменяется
Участок 3:
При 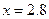
При 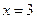
Значение продольной силы линейно уменьшается.
Найдем величины нормальных напряжений в характерных сечениях:
Участок 1:
При 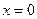
При 
Участок 2:
При 
Участок 3:
При 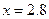
При 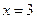
Величины абсолютных удлинений каждого их участков стержней найдем по формуле:
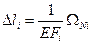
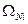
Определим величины осевых перемещений характерных сечений.
На участках 1 и 3 эпюра осевых перемещений имеет вид квадратичной параболы, на участке 2 изменяется линейно.
Пример 4. Для статически неопределимой стержневой системы, состоящей из абсолютно жесткой балки AB и поддерживающих ее стальных стержней 1 и 2 по схеме №…. при геометрических размерах, соотношениях площадей поперечных сечений стержней F2/F1 и величине нормативной нагрузки Р, указанных в строке № …. табл.2, требуется:
1.Определить расчетное значение нагрузки, приняв коэффициент надежности по нагрузке γf = 1,2.
2.Определить усилия в стержнях системы. Собственную массу элементов стержневой системы не учитывать.
3.Подобрать сечения стрежней в виде двух стальных прокатных равнобоких уголков, используя метод расчета по предельным состояниям. При подборе сечений обеспечить заданное соотношение площадей F2/F1. Расчетное сопротивление по пределу текучести стали марки ВСТ3 принять равным 210 МПа, коэффициент условий работы γс = 0,9.
4.Определить величины нормальных напряжений в поперечных сечениях стержней и проверить выполнение условий прочности.
5.Определить величины удлинений стержней, приняв Е=2,1·10 5 МПа.
6.Определить нагрузку Рт, при которой в системе возникают первые пластические деформации, считая, что материал стержней следует диаграмме Прандтля и имеет предел текучести σт = 240 МПа.
7.Определить разрушающую нагрузку Рразр, при которой система полностью исчерпывает свою несущую способность.
| a, м | b, м | h, м | F2/F1 | Р, кН |
| 1,4 | 0,8 | 1,3 | 1,3 |
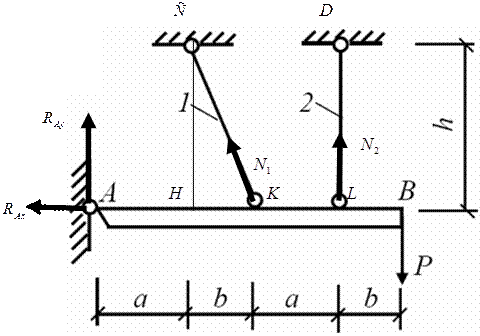
2. Определим усилия в стержнях. Система является статически неопределимой. Представим систему в деформированном виде. Рассмотрим:
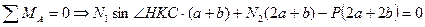
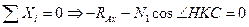
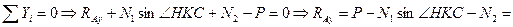
Отрицательные знаки говорят о том, что действительные направления сил противоположны указанным на чертеже.
Вычисляем напряжения в стержнях 1 и 2
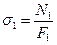
Определяем требуемые по условию прочности площади поперечных сечений
Проверим соотношение 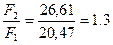
Принимаем по сортаменту сечения стержней в виде двух стальных прокатных равнобоких уголков.
Стержень 1: профиль №7, 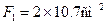
Стержень 2: профиль №10, 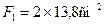
Определим удлинения стержней при
Определим нагрузку
Находим из уравнения равновесия величину Рразр:
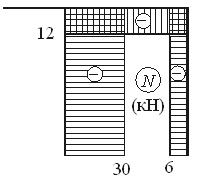
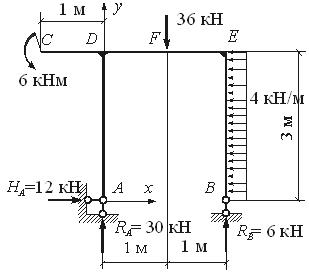
Пример 5. Для рамы с шарнирными опорами построим эпюры N,Q, и M.
Определяем величины опорных реакций.
| SX = 0 , | – 4·3 + HА = 0 , | HА = 12 кН ; |
| SMА = 0 | 6 – 36·1 + 4·3·1,5 + 2RВ = 0 , | RВ = 6 кН ; |
| SMВ = 0 , | 6 + 36 + 4·3·1,5 – 2RА = 0 , | RА = 30 кН ; |
| SU = 0 (проверка) , | – 36 + 30 + 6= – 36 + 36 = 0 . |
Определяем внутренние усилия в характерных сечениях каждого участка рамы.
| Участок АD | ||
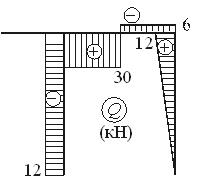
| Сечение А: | N = – RА = – 30 кН (сжатие), | Q = – HА= – 12 кН , M = 0 |
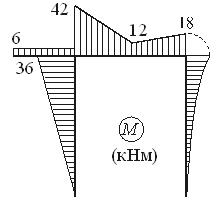
| Сечение D: | N = – 30 кН , Q = – 12 кН , | M = – 12*3 = – 36 кНм |
| (растянуты левые волокна). | ||
| Участок ВЕ | ||
| Сечение В: | N = – RА = – 6 кН , | Q = 0 , M = 0 , |
| Сечение E: | N = – 6 кН , Q = 4·3 = 12 кН , | M = – 4·3·1,5 = – 18 кНм |
| (растянуты правые волокна). | ||
| Участок CE | ||
| Сечение C: | N = 0 , Q = 0 , | M = – 6 кНм |
| (растянуты верхние волокна) . | ||
| Сечение D (слева): | N = 0 , Q = 0 , | M = – 6 кНм . |
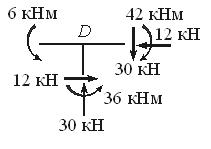
| Сечение D (справа): | N = – HА = – 12 кН , Q = RА = 30 кН , | M = – 6 – 12·3= – 42 кНм |
| Сечение F (слева): | N = – 12 кН , Q = 30 кН , | M= –42+30·1= – 12 кНм . |
| Сечение F (справа): | N = – 12 кН , Q = 30 – 36 = – 6 кН , | M = – 12 кНм . |
| Сечение Е: | N = – 12 кН , Q = – RВ = – 6 кН , | M = – 18 кНм . |
Построим эпюры N , Q , и M:
Вырежем мысленно узел D и покажем его равновесие под действием внутренних усилий в стержнях, сходящихся в узле. Нетрудно видеть, что узел находится в равновесии:
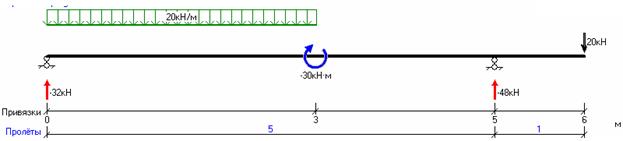
Пример 6. Рассчитать на прочность по методу предельных состояний двутавровую прокатную балку.
Материал балки сталь ВСт 3. Предел текучести σт = 240 МПа, расчетное сопротивление по пределу текучести R= 210 МПа, расчетное сопротивление при сдвиге Rs = 130 МПа. Коэффициент условий работы γс = 0,9. В табл. 2 приведены нормативные значения нагрузок. Коэффициент надежности по нагрузке γf = 1,2.
1.Определить опорные реакции;
2.Вычислить величины внутренних усилий в характерных сечениях и построить эпюры внутренних усилий.
3.Подобрать сечение балки из двутавра, используя условие прочности по первой группе предельных состояний.
1. Определим опорные реакции.
2. Проверка: 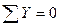
Реакции найдены правильно.
3. Построим эпюры Q и M.
Разобьем нашу балку на три участка и найдем суммы сил и моментов, действующих на каждом участке.
I участок:
II участок:
III участок: 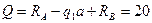
В конце балки
I участок: 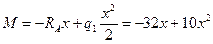
II участок: 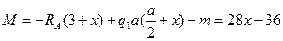
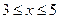
III участок: 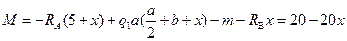
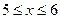
На участке 1 эпюра М имеет вид квадратичной параболы, ветви которых направлены вверх.
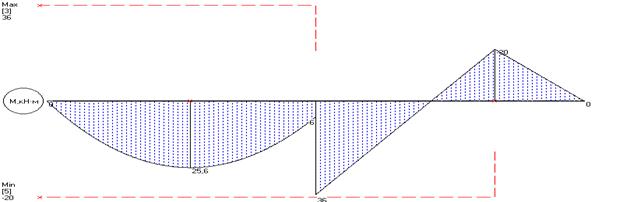
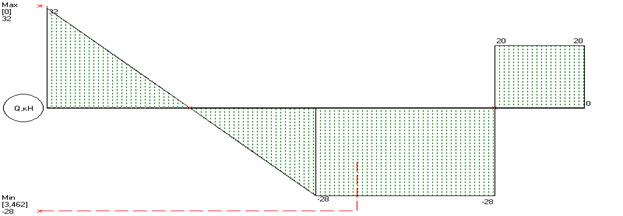
Построим схему конструкции и эпюры Q и M:
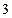
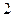
Значения М и Q в характерных сечениях балки указаны на эпюрах.
Опасным является сечение в точке с координатой 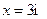
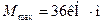
Требуемый момент сопротивления равен
По сортаменту прокатной стали принимаем двутавровый профиль № 22
h=220мм, b=110мм, d=5.4мм, t=8.7мм, Jx=2550см 4 , W=232см 3 , Sx=131см 3
Вычислим значения наибольших нормальных напряжений в опасном сечении балки:
Прочность балки обеспечена.
6. Задания для контрольной работы
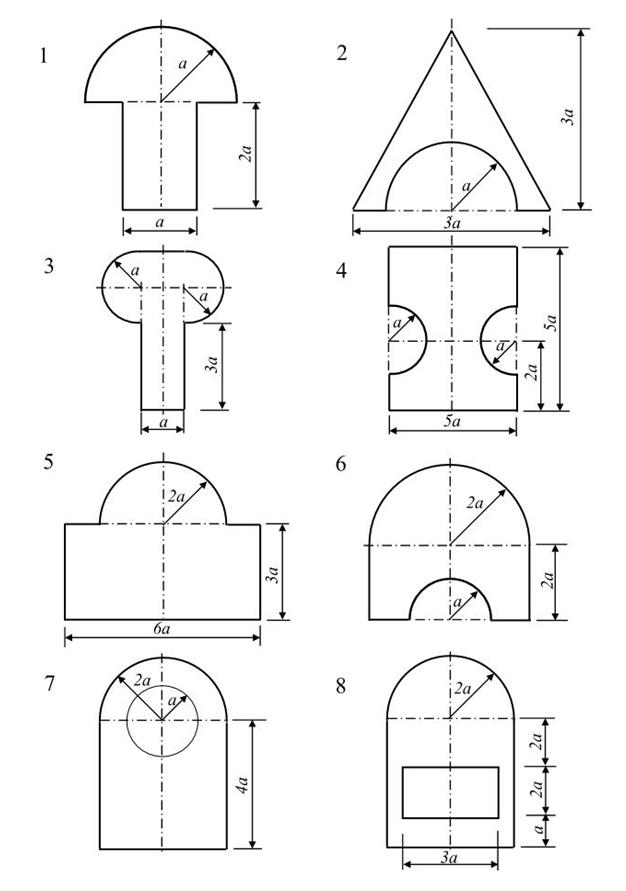
Для сечений, имеющих одну ось симметрии, по схемам №1-16 при размерах, указанных в таблице 2, требуется определить:
1) положение центра тяжести;
2) положение главных центральных осей инерции и величины главных моментов инерции.
| Первая буква фамилии студента | а, см |
| А | П |
| Б | Р |
| В | С |
| Г | Т |
| Д | У |
| Е | Ф |
| Ж | Х |
| З | Ц |
| И | Ч |
| К | Ш |
| Л | Щ |
| М | Э |
| Н | Ю |
| О | Я |
Схемы сечений стержней:
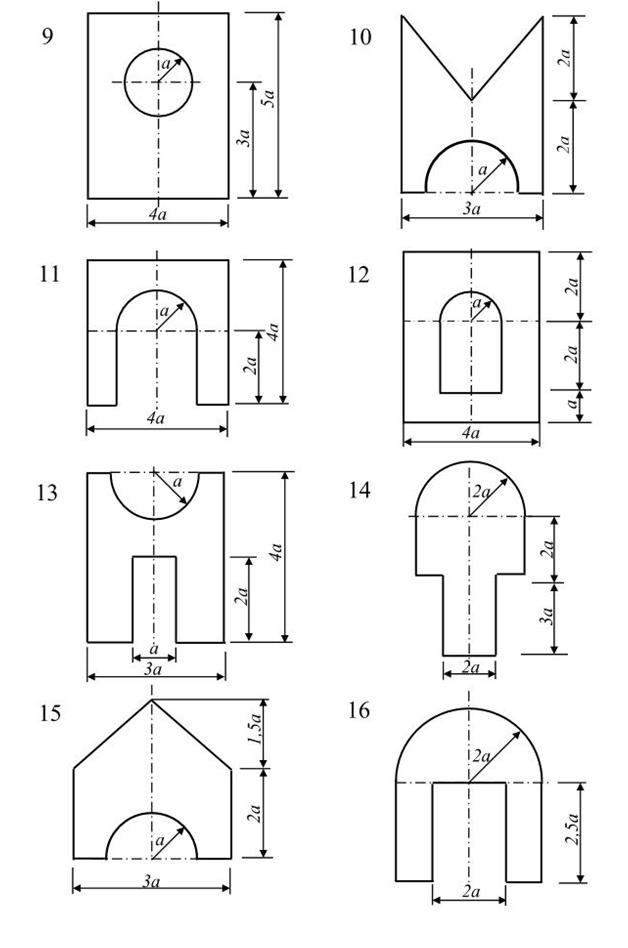
Для несимметричных сечений по схемам №1-16 при размерах, указанных в таблице 3, требуется:
1) определить положение центра тяжести;
2) вычислить осевые и центробежные моменты инерции относительно центральных осей;
3) определить положение главных центральных осей инерции и величины главных моментов инерции;
4) построить круг инерции и определить графически величины главных моментов инерции и направления главных центральных осей;
5) сравнить результаты аналитического и графического расчетов.
- Момент инерции сечения
- Моменты инерции сечения из простых фигур
- Вывод моментов инерции для простых фигур
- Моменты инерции для прямоугольника
- #Сопромат, Моменты инерции. Прямоугольник. Вывод моментов инерции для прямоугольника.
- Моменты инерции для треугольника
- Сопротивление материалов, Моменты инерции для треугольника. Сопромат вывод моментов инерции
- Момент инерции круга. Моменты инерции простых фигур. #сопромат
- Моменты инерции. Оси центральные и главные. Что это и где. #сопромат
- Примеры расчетов моментов инерции для сечений
- Пример расчета моментов инерции относительно главных центральных осей для простейших фигур
- Пример расчета моментов инерции для сечения состоящего из прямоугольника и треугольника
- Расчет моментов инерции сечения составного из стандартных прокатных профилей
- 1. Вывод формул для моментов инерции простейших фигур (прямоугольник, треугольник, круг) Прямоугольное сечение
- 💡 Видео
Видео:Геометрические характеристики. Моменты инерции. Радиусы инерции. Сопромат.Скачать

Момент инерции сечения
Меня часто спрашивают: «…а что такое моменты инерции в сопротивлении материалов и зачем они вообще?» Об этом в сегодняшней теме
Видео:Моменты инерции относительно Главных Центральных осей для простых фигурСкачать

Моменты инерции сечения из простых фигур
Начнем с моментов инерции простых фигур и на их примере выясним для сложных фигур и составных сечений из стандартных профилей.
Начать объяснение о том, что такое моменты инерции нужно с того, что спросить, а что такое площадь?
Обычная площадь квартиры, огорода сечения стержня? Зачем она и почему?
Так вот площадь это характеристика которую придумали и вывели для разных фигур, чтобы была возможность сравнивать земельные наделы. Не всегда они были прямоугольные или квадратные. А сравнить кто сколько получил в надел было нужно. Вот и вывели такую закономерность для прямоугольника, что если перемножить стороны — получим величину, которую можно будет сравнить с перемноженной высотой на основание деленное пополам для треугольника или для круга Пи умножить на эр в квадрате )). Т.е. площади простых фигур
Что касается моментов инерции в сопротивлении материалов, то тут они появились, когда стало понятно, что есть какая то геометрически измеримая величина для разных форм сечения, которая позволит сравнить сопротивляемость этих сечений изгибу.
Проще говоря бревно, которое выполняет роль балки и изгибается может иметь форму прямоугольника, квадрата или круга, а нам нужно сравнить их сопротивляемость изгибу. Вот для этих целей выводили формулу напряжений и оказалось, что в числителе оказался изгибающий момент, а в знаменателе момент инерции:
на балке изображены главные центральные оси z y
прогибы для таких балок будут разными относительно осей z и y, т.к. моменты инерции будут разные.
Видео:Моменты инерции простейших фигур. Оси центральные и главные. Что это и где. #сопроматСкачать

Вывод моментов инерции для простых фигур
Так вот ниже я приведу видео уроки, плейлист, в котором один за одним выведены моменты инерции для простых фигур, а именно для прямоугольника, треугольника и круга. А затем приводится стандартный расчет моментов инерции для более сложной фигуры, которая состоит из нескольких простых. Всегда сложную фигуру можно разбить на несколько простых. Исходя из этого расчет и ведется.
Моменты инерции измеряются в единицах длины в 4 степени, т.е. см⁴ или м⁴. Чаще всего используется см⁴, т.к. такие единицы измерения приведены в сортаменте прокатной стали.
Момент инерции, это величина, которая показывает сопротивляемость сечения изгибу. На примере линейки хорошо понятно что изгиб в одной плоскости и изгиб в другой плоскости будут сильно отличаться, хотя площадь сечения не меняется. Вот это и было выведено в формуле для напряжений и для прогибов. Что величина, которая сопротивляется изгибающему моменту есть интеграл до координаты центра тяжести площадки в квадрате на площадь элементарной площадки.
Центральными осями называют оси, которые проходят через центр тяжести сечения
Главные оси располагаются в сечении таким образом, что центробежный момент относительно них равен нулю. Т.е. это максимальный и минимальный осевые моменты инерции
Оси, которые проходят через центр тяжести сечения и центробежный момент инерции относительно них равен нулю. При этом данные осевые моменты инерции являются экстремальными, т.е. имеют максимальное и минимальное значение. Именно относительно этих осей ведут расчет и к ним приводят нагрузки. Т.е. если какое нибудь внешнее усилие проходит в стороне от главных центральных осей. Это усилие переносят соблюдая правила переноса к главным центральным осям. Только после этого рассматривают действие сил и находят внутренние усилия относительно главных центральных осей инерции.
При вычислении моментов инерции осевых, при переходе от одних осей к другим появляется центробежный момент инерции, как составляющая пары осевых моментов инерции. И только для главных осей центробежные моменты инерции равны нулю. Именно эти оси мы и отыскиваем в наших расчетах. Поэтому мы ищем величину центробежного момента инерции для не главных осей и из свойства, что главные центральные оси это такие оси, относительно которых центробежный момент инерции равен нулю, находим положение главных центральных осей.
Видео:Моменты инерции относительно Главных Центральных осей для составной фигурыСкачать

Моменты инерции для прямоугольника
Видео:Теория (часть 1) осевые моменты инерцииСкачать

#Сопромат, Моменты инерции. Прямоугольник. Вывод моментов инерции для прямоугольника.
Сопротивление материалов и Моменты инерции для прямоугольника. Понятие моментов инерции, формулы и вывод для прямоугольника. Осевые центробежный моменты инерции. для треугольника вывод моментов инерции в этом видео: https://www.youtube.com/embed/_pixohVoc-4?vq=hd720 Тема моментов инерции возникла в связи стем, что для определения напряжений при изгибе понадобилась геометрическая характеристика, которая сопротивляется внутреннему усилию (изгибающему моменту). В результате вывода формулы напряжений и появилась эта формула, выраженная через интеграл от квадрата координаты помноженной на площадь элементарной площадки. Эту геометрическую характеристику и назвали моментом инерции. пройти полный курс обучения сопромату и строймеху онлайн, по скайпу. Задать вопросы можно: — через сайт: https://stroymex.online — skype: zabolotnyiAN — email: zabolotnyiAN@gmail.com — комменты к видео — Телеграм https://t.me/AleksanderCrafts Телеграм канал: https://t.me/sroymexOnline Не тратьте время зря, задавайте вопросы. Узнайте стоимость обучения: https://stroymex.online/usloviya-i-tsena-onlayn-obucheniya-sopromat-i-stroymeh Получите первую консультацию бесплатно! Facebook: https://www.facebook.com/SopromatOnline
2018-04-09
моменты инерции для прямоугольника для главных центральных осей равны, формула
моменты инерции для прямоугольника для осей проходящих через основные размеры равны, формула
Моменты инерции для треугольника
Видео:Сопротивление материалов. Лекция: геометрические характеристики сечений - моменты инерцииСкачать

Сопротивление материалов, Моменты инерции для треугольника. Сопромат вывод моментов инерции
Сопротивление материалов и Моменты инерции для треугольника. Сопромат вывод моментов инерции для простых фигур. Моменты инерции для треугольника. Моменты инерции для осей в треугольнике, которые проходят через основные размеры. Вывод и пояснение к этой теме сопротивления материалов. для прямоугольника вывод моментов инерции в этом видео: https://www.youtube.com/watch?v=v1TE1UW_sRE&feature=youtu.be Тема моментов инерции возникла в связи стем, что для определения напряжений при изгибе понадобилась геометрическая характеристика, которая сопротивляется внутреннему усилию (изгибающему моменту). В результате вывода формулы напряжений и появилась эта формула, выраженная через интеграл от квадрата координаты помноженной на площадь элементарной площадки. Эту геометрическую характеристику и назвали моментом инерции. пройти полный курс обучения сопромату и строймеху онлайн, по скайпу Задать вопросы можно: — через сайт: https://stroymex.online — skype: zabolotnyiAN — email: zabolotnyiAN@gmail.com — комменты к видео — Телеграм https://t.me/AleksanderCrafts Телеграм канал: https://t.me/sroymexOnline Не тратьте время зря, задавайте вопросы. Узнайте стоимость обучения: https://stroymex.online/usloviya-i-tsena-onlayn-obucheniya-sopromat-i-stroymeh Получите первую консультацию бесплатно! Facebook: https://www.facebook.com/SopromatOnline
2018-04-09
Моменты инерции треугольника относительно произвольых осей
Видео:Стереометрия 10 класс. Часть 1 | МатематикаСкачать

Момент инерции круга. Моменты инерции простых фигур. #сопромат
Вывод моментов инерции для круга. Видео урок из темы «Моменты инерции простых фигур». В видео приведен вывод момента инерции полярного, в полярной системе координат Ip Затем выведены моменты инерции осевые Iz, Iy. Задать вопросы можно: — через сайт: https://stroymex.online — skype: zabolotnyiAN — email: zabolotnyiAN@gmail.com — комменты к видео — Телеграм https://t.me/AleksanderCrafts Телеграм канал: https://t.me/sroymexOnline Не тратьте время зря, задавайте вопросы. Узнайте стоимость обучения: https://stroymex.online/usloviya-i-tsena-onlayn-obucheniya-sopromat-i-stroymeh Получите первую консультацию бесплатно! Facebook: https://www.facebook.com/SopromatOnline
2019-09-14
Видео:Определение положения главных центральных осей и главных центральных моментов инерцииСкачать
Моменты инерции. Оси центральные и главные. Что это и где. #сопромат
Центральные оси — любая пара взаимно перпендикулярных осей, которые проходят через центр тяжести фигуры Главные оси — оси для которых центробежный момент инерции равен нулю, а осевые моменты имеют максимум и минимум. Об этом и многом другом в видео уроке по моментам инерции в сопротивлении материалов Задать вопросы можно: — через сайт: https://stroymex.online — skype: zabolotnyiAN — email: zabolotnyiAN@gmail.com — комменты к видео — Телеграм https://t.me/AleksanderCrafts Телеграм канал: https://t.me/sroymexOnline Не тратьте время зря, задавайте вопросы. Узнайте стоимость обучения: https://stroymex.online/usloviya-i-tsena-onlayn-obucheniya-sopromat-i-stroymeh Получите первую консультацию бесплатно! Facebook: https://www.facebook.com/SopromatOnline
2019-09-14
Видео:Основы Сопромата. Геометрические характеристики поперечного сеченияСкачать

Примеры расчетов моментов инерции для сечений
Ниже приводятся примеры расчетов моментов инерции относительно главных центральных осей, объяснение, что такое центробежный момент инерции и почему оси называются главными центральными для примеров:
- простейшие фигуры — прямоугольник, треугольник
- составные сечения из простейших треугольника и прямоугольника
- составные из прокатных профилей
Пример расчета моментов инерции относительно главных центральных осей для простейших фигур
Подробно объясняется как найти центробежный момент инерции, как найти осевые моменты инерции, как относительно центральных и как относительно главных осей для простых фигур.
Пример расчета моментов инерции для сечения состоящего из прямоугольника и треугольника
Сечения балок может быть составным, т.е. таким, которое складывается из нескольких фигур. В примере, в видеоуроке ниже рассказыватся как найти моменты инерции относительно главных центральных осей для такого сечения балки
Расчет моментов инерции сечения составного из стандартных прокатных профилей
В видеоуроке ниже разбирается порядок расчета моментов инерции относительно главных центральных осей для сечения составленого из трех прокатных профилей уголков
Видео:Вычисление моментов инерции составного сеченияСкачать

1. Вывод формул для моментов инерции простейших фигур (прямоугольник, треугольник, круг) Прямоугольное сечение
| Название | 1. Вывод формул для моментов инерции простейших фигур (прямоугольник, треугольник, круг) Прямоугольное сечение |
| Анкор | otvety_po_sopromatu.doc |
| Дата | 20.03.2018 |
| Размер | 0.73 Mb. |
| Формат файла |  |
| Имя файла | otvety_po_sopromatu.doc |
| Тип | Документы #16947 |
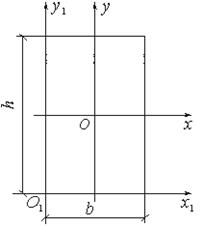
| Подборка по базе: Расчёт элементов конструкции автомобильных дорог из композита (Д, доклад Лавриненко В. 9а на тему_Стресс и способы вывода себя из , 10 тема. Основные формулы тригонометрии.docx, бирка на формуляры.docx, схемы вывода.docx, Теория моментов инерции.doc, Устройства вывода информации.doc, 122 формулы по физике.pdf, питание формула.pdf, № 1 Красная кровь Лейкоцитарная формула-2.doc 1. Вывод формул для моментов инерции простейших фигур (прямоугольник, треугольник, круг) Прямоугольное сечение имеет две оси симметрии, а главные центральные оси Сx и Cy проходят через середины параллельных сторон. Главный центральный момент инерции относительно оси x Элементарную площадку dA в этом случае можно представить в виде полоски во всю ширину сечения и толщиной dy, значит dA=b*dy. Подставим под знак интеграла значение dA и проинтегрировав по всей площади, т.е. в пределах изменения ординаты y от –h/2 до +h/2, получим Аналогично получим формулу главного центрального момента инерции прямоугольника относительно оси y:
Для круга главные центральные моменты инерции относительно осей x и y равны между собой. Поэтому из равенства 2.Изменение моментов инерции при переходе от центральных осей к параллельным: Jy1=Jy + b 2 А; Jx1y1= Угол >0, если переход от старой системы координат к новой происходит против час.стр. Jy1 + Jx1= Jy + Jx Экстремальные (максимальное и минимальное) значения моментов инерции называются главными моментами инерции. Оси, относительно которых осевые моменты инерции имеют экстремальные значения, называются главными осями инерции. Главные оси инерции взаимно перпендикулярны. Центробежные моменты инерции относительно главных осей = 0, т.е. главные оси инерции — оси, относительно которых центробежный момент инерции = 0. Если одна из осей совпадает или обе совпадают с осью симметрии, то они главные. Угол, определяющий положение главных осей: 0>0 оси поворачиваются против час.стр. Ось максимума всегда составляет меньший угол с той из осей, относительно которой момент инерции имеет большее значение. Главные оси, проходящие через центр тяжести, называются главными центральными осями инерции. Моменты инерции относительно этих осей: Jmax + Jmin= Jx + Jy. Центробежный момент инерции относительно главных центральных осей инерции равен 0. Если известны главные моменты инерции, то формулы перехода к повернутым осям: Jx1=Jmaxcos 2 + Jminsin 2 ; Jy1=Jmaxcos 2 + Jminsin 2 ; Jx1y1= 4.Классификация элементов конструкций Стержнем наз. Геом тела у которых один из размеров много больше других. Пластины или оболочки – это геом тела у которых один из размеров 0 эпюра мх возрастает слева направо 5. В том сеч. где приложена сосред сила эпюра Qy имеет скачок на вел этой силы. В сеч где сосред момент эпюра мх имеет скачок на величену этого момента 14.Понятие о напряжениях. Нормальные и касательные напряжения Напряжение – численная мера распределения внутренних сил по плоскости поперечного сечения. Его используют при исследовании и определении внутренних сил любой конструкции. Выделим на плоскости сечения площадку A; по этой площадке будет действовать внутренняя сила R. Величина отношения R/A=pсрназывается средним напряжением на площадке A. Истинное напряжение в точке А получим устремив A к нулю: Нормальные напряжения возникают, когда частицы материала стремятся отдалиться друг от друга или, наоборот, сблизиться. Касательные напряжения связаны со сдвигом частиц по плоскости рассматриваемого сечения. Очевидно, что 16.Закон парности касательных напряжений Касат. напряжение на 2-ух взаимно перпендик. площ. направлены к ребру или от ребра и равны по величине 17.Понятие о деформациях. Мера линейной, поперечной и угловой деформации Деформац – наз. взаимное перемещение точек или сечений тела по сравн с полож-ями тела которые они занимали до приложения внеш сил бывают: упругие и пластические а) линейная деформация мерой явл относительное удлинение эпсила =l1-l/l б) поперечная деф мерой явл. относительное сужение эпсила штрих=|b1-b|/b 18.Гипотеза плоских сечений Основные гипотезы (допущения): гипотеза о не надавливании продольных волокон: волокна, параллельные оси балки, испытывают деформацию растяжения – сжатия и не оказывают давления друг на друга в поперечном направлении; гипотеза плоских сечений: сечение балки, плоское до деформации, остается плоским и нормальным к искривленной оси балки после деформации. При плоском изгибе в общем случае возникают внутренние силовые факторы: продольная сила N, поперечная сила Q и изгибающий момент М. N>0, если продольная сила растягивающая; при М>0 волокна сверху балки сжимаются, снизу растягиваются. Слой, в котором отсутствуют удлинения, называется нейтральным слоем (осью, линией). При N=0 и Q=0, имеем случай чистого изгиба. Нормальные напряжения: 19.Закон Гука (1670). Физический смысл входящих в него величин Он установил связь между напряжением, растяжением и продольной деформацией. Модуль упругости характеризует жёсткость материала, т.е. способность сопротивляться деформациям. (чем больше Е, тем менее растяжимый материал) Потенциальная энергия деформации: Внешние силы, приложенные к упругому телу, совершают работу. Обозначим её через А. В результате этой работы накапливается потенциальная энергия деформированного тела U. Кроме того, работа идёт на сообщение скорости массе тела, т.е. преобразуется в кинетическую энергию К. Баланс энергии имеет вид А = U + К. 20.Три стороны задачи определения напряжений при выводе формулы опр напр необходимо расм 3 стороны задачи устанавливает закон распределения деформации по сеч бруса 2) Физическая (ФС) 3) Статическая сторона (СС) связ-ет напр с ВСФ(внутр сил фактор) посредствам зависимостей 21.Простое осевое растяжение – сжатие
22.Формула для определения деформации бруса при растяжении-сжатии. Жесткость сечения бруса и физический смысл входящих в формулу величин Опр-е деформации бруса при раст-сжатии из (**) ЕА-жесткая сечение бруса при растяжении-сжатии 24.Формула для определения угла закручивания круглого бруса. Жесткость сечения бруса и физический смысл входящих в формулу величин 25.Кручение брусьев прямоугольного сечения Wk- αhb^2 -момент сопротивления кручению Jk- βhb^3 –момент инерции при кручении для c hb >10 α≈β≈13 26.Кручение тонкостенных стержней открытого и закрытого профиля Характерной геометрической особенностью тонкостенных стержней является то, что их толщина существенно (на порядок и более) меньше других геометрических размеров тонкостенное кольцо закрытого профиля Характер распределения напряжений по толщине тонкостенного стержня открытого профиля близок к равномерному (рис. 4.7, б), а замкнутого профиля меняется по линейному закону, как это показано на рис. 4.7, а. Откуда следует, что напряжения в поперечных сечениях открытого профиля практически не изменятся, если профиль сечения распрямить. Иначе говоря, напряжения в криволинейном открытом профиле будут примерно такими же, как и в прямом. 27.Прямой чистый изгиб Все элементы конструкции подвергаются изгибу, они все рассчитываются на изгиб. При этом используют расчетную схему конструкции (наиболее распространенная расчетная схема для множества конструкций — балка на двух опорах). Балка – брус, который воспринимает поперечные нагрузки и работает на изгиб. Допущения при изгибе:
Чистый изгиб – когда в поперечных сечениях балки действует только изгибающий момент (частный случай). Поперечный изгиб – когда в поперечных сечениях действует одновременно и изгибающий момент и поперечная сила (общий случай). Плоский (прямой) изгиб — когда изгибающий момент действует в плоскости, проходящей через одну из главных центральных осей инерции сечения, т.е. все силы лежат в плоскости симметрии балки. Основные гипотезы (допущения): гипотеза о не надавливании продольных волокон: волокна, параллельные оси балки, испытывают деформацию растяжения – сжатия и не оказывают давления друг на друга в поперечном направлении; гипотеза плоских сечений: сечение балки, плоское до деформации, остается плоским и нормальным к искривленной оси балки после деформации. При плоском изгибе в общем случае возникают внутренние силовые факторы: продольная сила N, поперечная сила Q и изгибающий момент М. N>0, если продольная сила растягивающая; при М>0 волокна сверху балки сжимаются, снизу растягиваются. Слой, в котором отсутствуют удлинения, называется нейтральным слоем (осью, линией). При N=0 и Q=0, имеем случай чистого изгиба. Нормальные напряжения: Максимальные напряжения при изгибе возникают в точках, наиболее удаленных от нейтрального слоя: Если сечение не имеет горизонтальной оси симметрии, то эпюра нормальных напряжений не будет симметричной. Нейтральная ось сечения проходит через центр тяжести сечения. Формулы для определения нормального напряжения для чистого изгиба приближенно годятся и когда Q0. Это случай поперечного изгиба. При поперечном изгибе, кроме изгибающего момента М, действует поперечная сила Q и в сечении возникают не только нормальные , но и касательные напряжения. Касательные напряжения определяются формулой Журавского: Для прямоугольного сечения: k— коэфф., зависящий от формы сечения (прямоугольник: k= 1,5; круг — k= 1,33). Mmax и Qmax определяются из эпюр изгибающих моментов и поперечных сил. Для этого балка разрезается на две части и рассматривается одна из них. Действие отброшенной части заменяется внутренними силовыми факторами М и Q, которые определяются из уравнений равновесия. В некоторых вузах момент М>0 откладывается вниз, т.е. эпюра моментов строится на растянутых волокнах. При Q= 0 имеем экстремум эпюры моментов. Дифференциальные зависимости между М,Q и q: q — интенсивность распределенной нагрузки [кН/м] Главные напряжения при поперечном изгибе:
из (*)и(**) 28.Понятие плоского поперечного изгиба. Расчетная формула для определения напряжений Чистый изгиб – вид нагружения, когда в поперечном сечении балки действует только изгибающий момент. Поперечный изгиб – когда на поперечное сечение действует одновременно изгибающий момент и поперечная сила (общий случай). Пример чистого изгиба: 29.Определение касательных напряжений при плоском поперечном изгибе Касательные напряжения определяются формулой Журавского: 30.Распределение касательных напряжений в прямоугольном, двутавровом и швеллерном сечении а) прямоугольное сеч б) двутавровое сеч г) швеллерное сеч 31.Роль касательных напряжений в балках, работающих на изгиб напряжение во 2 балке больше в 2 раза 32.Механические испытания материалов. Характеристики прочности материала По диаграмме растяжения оцениваются механические характеристики материала. Деформация рассматривается для упругопластичного материала (малоуглеродистая сталь). т. В – предел упругости т. С – предел текучести т. D – временный предел прочности; т. Е – разрушение образца. СD – зона упрочнения. Здесь удлинение образца сопровождается возрастанием нагрузки, но неизмеримо более медленным (в сотни раз), чем на упругом участке. т. D соответствует максимальному напряжению, при котором материал не разрушается. т. E – соответствует разрушению образца. tg Этот метод измерения характеристик материала самый простой, широкоиспользуемый и доступный. Способность материала без разрушения получать большие остаточные деформации носит название пластичности. Свойство пластичности имеет решающее значение для таких технологических операций, как штамповка, вытяжка, волочение, гибка и др. Мерой пластичности является удлинение Свойством, противоположным пластичности, является хрупкость, т.е. способность материала разрушаться без образования заметных остаточных деформаций. Материалы, обладающие этим свойством, называются хрупкими. Диаграмма растяжения хрупких материалов не имеет площади текучести и зоны упрочнения. Под твёрдостью понимается способность материала противодействовать механическому проникновению в него посторонних тел. Наиболее широкое распространение получили методы измерения твёрдости по Бринеллю и по Роквеллу. а) Твёрдость по Бринеллю [НВ] – в поверхность исследуемой детали вдавливают стальной шарик диаметром 10 мм. б) Твёрдость по Роквеллу [HRC]– алмазный острый наконечник. В результате испытаний на твёрдость удаётся определить прочностные показатели материала, не разрушая деталь. Характеристиками пластичности материала являются относительное удлинение и относительное сужение при разрыве: где l0, F0 — длина рабочей части образца и площадь поперечного сечения до деформации; lк — длина рабочей части образца после разрыва; F0 — конечная площадь поперечного сечения в шейке образца после разрыва. 34.Предельные и допускаемые напряжения При проектировании элемента конструкции необходимо определить размеры, обеспечивающие его безопасную работу при заданных нагрузках. Для успешного решения этой задачи необходимо исходить из того, чтобы наибольшее расчётное напряжение в поперечном сечении элемента конструкции, возникшее при заданной нагрузке, было меньше того предельного напряжения, при котором возникает опасность появления пластической деформации или опасность разрушения. Отношение предельного напряжения
При расчёте элемента конструкции коэффициент запаса прочности задаётся заранее и называется нормативным или требуемым и обозначается [s]. Прочность элемента конструкции обеспечивается, если действительный коэффициент запаса прочности не ниже требуемого т.е. Это неравенство выражает условие прочности элемента конструкции. Разделив предельное напряжение на нормальный коэффициент запаса, получим допускаемое напряжение Тогда условие прочности можно выразить неравенством т.е. прочность элемента конструкции обеспечивается, если наибольшее напряжение, возникающее в нём, не превышает допускаемого. условия прочности при простейших деформациях
3 типа задач при расчете на прочность
пример опр размер поп сечения бруса квадр сеч. 40. Определение главных напряжений в брусьях при растяжении-сжатии, кручении, изгибе 💡 ВидеоОпределение осевых моментов инерции составного несимметричного сечения. СопроматСкачать  Моменты инерции для треугольника. Вывод моментов инерции для треугольниковСкачать  Осевая симметрия. 6 класс.Скачать  Моменты инерции сечения из простых фигурСкачать  Момент инерцииСкачать  Треугольник и окружность #shortsСкачать  Определение центра тяжести сложной фигуры. СопроматСкачать  Моменты инерции Прямоугольника ► Вывод моментов инерции для прямоугольникаСкачать  Частное положение точек. Точки принадлежащие к плоскостям проекции.Скачать  | |||||||||||||||||||||||||||||
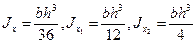
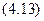
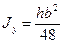
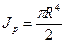
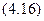
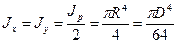
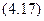
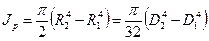
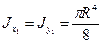
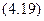
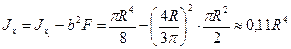
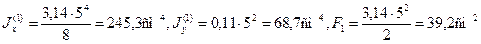
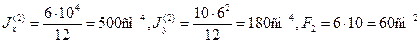
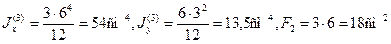
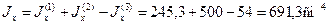
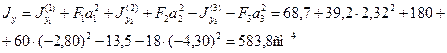
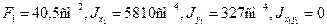
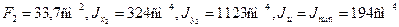
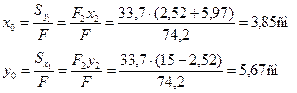
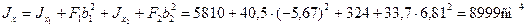
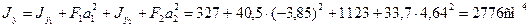
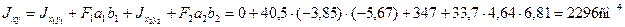
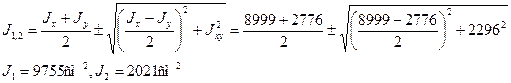
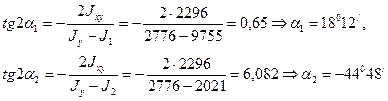
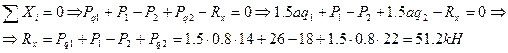
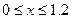
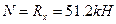
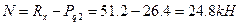
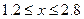
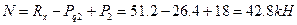
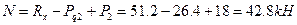
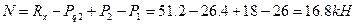
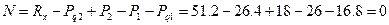
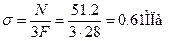
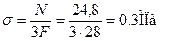
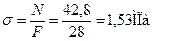
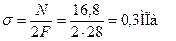
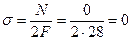
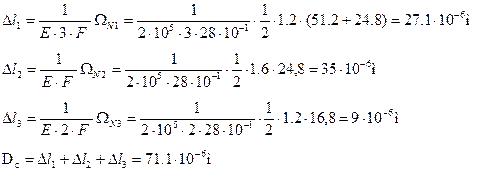
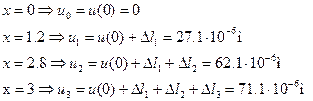

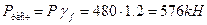
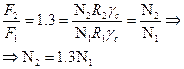
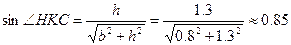
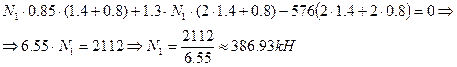
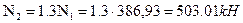
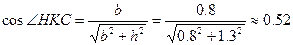
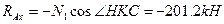
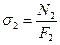
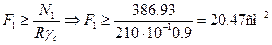
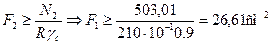
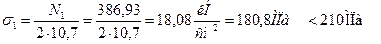
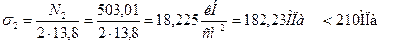
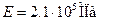
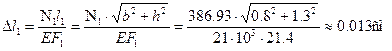
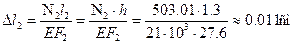
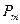
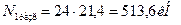
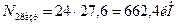
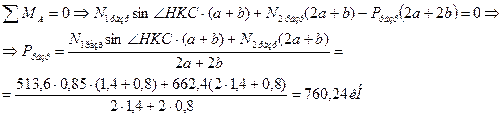
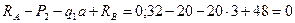
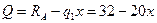
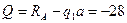
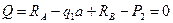
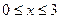
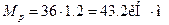
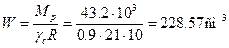
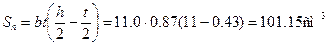
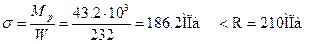


























 (Jx — Jy)sin2 + Jxycos2 ;
(Jx — Jy)sin2 + Jxycos2 ; , если
, если

 . Касательное напряжение в свою очередь может быть разложено по направлениям осей x и y (τzх, τzу). Размерность напряжений – Н/м 2 (Па).
. Касательное напряжение в свою очередь может быть разложено по направлениям осей x и y (τzх, τzу). Размерность напряжений – Н/м 2 (Па). 
 .
. , — радиус кривизны нейтрального слоя, y — расстояние от некоторого волокна до нейтрального слоя.
, — радиус кривизны нейтрального слоя, y — расстояние от некоторого волокна до нейтрального слоя. где Е – коэффициент пропорциональности (модуль упругости материала).
где Е – коэффициент пропорциональности (модуль упругости материала).


 — ф-ла для определения напряжения раст-сжатии
— ф-ла для определения напряжения раст-сжатии










 , откуда (формула Навье):
, откуда (формула Навье):  , Jx — момент инерции сечения относительно главной центральной оси, перпендикулярной плоскости изгибающего момента, EJx — жесткость при изгибе,
, Jx — момент инерции сечения относительно главной центральной оси, перпендикулярной плоскости изгибающего момента, EJx — жесткость при изгибе,  — кривизна нейтрального слоя.
— кривизна нейтрального слоя. , Jx/ymax=Wx—момент сопротивления сечения при изгибе,
, Jx/ymax=Wx—момент сопротивления сечения при изгибе,  .
. , где Sx(y) — статический момент относительно нейтральной оси той части площади, которая расположена ниже или выше слоя, отстоящего на расстоянии «y» от нейтральной оси; Jx — момент инерции всего поперечного сечения относительно нейтральной оси, b(y) — ширина сечения в слое, на котором определяются касательные напряжения.
, где Sx(y) — статический момент относительно нейтральной оси той части площади, которая расположена ниже или выше слоя, отстоящего на расстоянии «y» от нейтральной оси; Jx — момент инерции всего поперечного сечения относительно нейтральной оси, b(y) — ширина сечения в слое, на котором определяются касательные напряжения.
 , F=bh, для круглого сечения:
, F=bh, для круглого сечения: , F=R 2 , для сечения любой формы
, F=R 2 , для сечения любой формы  ,
,


 .
. -формула для вычисления норм напр при прямом чистом изгибе
-формула для вычисления норм напр при прямом чистом изгибе
 — удельная нагрузка, приходящаяся на единицу длины конструкции.
— удельная нагрузка, приходящаяся на единицу длины конструкции. , где Qy-поперечная сила; Sx(y) — статический момент отсеченной части бруса относительно нейтральной оси той части площади, которая расположена ниже или выше слоя, отстоящего на расстоянии «y» от нейтральной оси; Jx — момент инерции всего поперечного сечения относительно нейтральной оси, b(y) — ширина сечения в слое, на котором определяются касательные напряжения.
, где Qy-поперечная сила; Sx(y) — статический момент отсеченной части бруса относительно нейтральной оси той части площади, которая расположена ниже или выше слоя, отстоящего на расстоянии «y» от нейтральной оси; Jx — момент инерции всего поперечного сечения относительно нейтральной оси, b(y) — ширина сечения в слое, на котором определяются касательные напряжения.




 ;
; ;
; ;
; .
. — даёт модуль упругости.
— даёт модуль упругости. при разрыве. Чем больше
при разрыве. Чем больше 

 к расчётному
к расчётному  называется коэффициентом запаса прочности s:
называется коэффициентом запаса прочности s: .
. :
:



 ;
;








