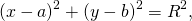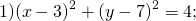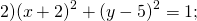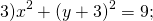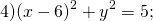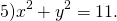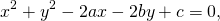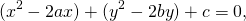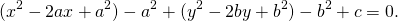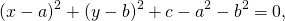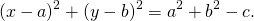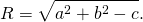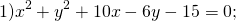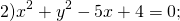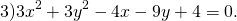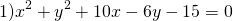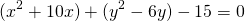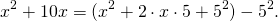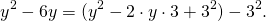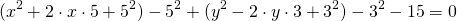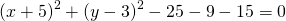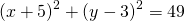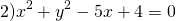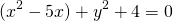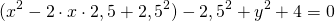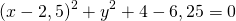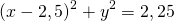Найти радиус окружности если она проходит через точку

Геометрия | 5 — 9 классы

Найдите радиус окружности, если она проходит через точку ( — 2 ; 1) и ее центр находится в точке (2 ; — 3).

(x — 2)² + (y + 3)² = ( — 2 — 2)² + (1 + 3)² ; (x — 2)² + (y + 3)² = (4√2)².

Найдите радиус окружности проходящей через точку А(12 ; 20) и с центром в точке С(5 ; — 4)?

Найдите радиус окружности проходящей через точку А(12 ; 20) и с центром в точке С(5 ; — 4).

Через точку A к окружности проведены AB (точка B лежит на окружности) и секущая, которая пересекает окружность в точках E и F и проходит через центр окружности?

Через точку A к окружности проведены AB (точка B лежит на окружности) и секущая, которая пересекает окружность в точках E и F и проходит через центр окружности.

Найдите радиус окружности, если AB = 12, AF = 18 /.

Найдите расстояние от точки А до ближайшей к ней точки окружности с центром О радиуса R, если ОА = 12см, а радиус = 8?

Найдите расстояние от точки А до ближайшей к ней точки окружности с центром О радиуса R, если ОА = 12см, а радиус = 8.

Радиус окружности с центром О равен 3 см?

Радиус окружности с центром О равен 3 см.

Прямая а проходит через точку К и касается окружности в точке М.

Найдите длину отрезка КМ, учитывая что КО = 5см.

Из точки А к окружности с центром в точке О проведена касательная, которая касается окружности в точке В?

Из точки А к окружности с центром в точке О проведена касательная, которая касается окружности в точке В.

Найдите радиус окружности, если АВ = 8см, АО = 17см.

Окружность с центром в начале координат проходит через точку (5 ; 5) чему равен радиус окружности?

Окружность с центром в начале координат проходит через точку (5 ; 5) чему равен радиус окружности.

Найдите уравнение окружности , которая проходит через точку F(5, — 2) и центр который находится в точке С ( — 1, 1)?

Найдите уравнение окружности , которая проходит через точку F(5, — 2) и центр который находится в точке С ( — 1, 1).

Помогите пожалуйста найдите радиус окружности, если она проходит через точку ( — 2 ; 1) и ее центр находится в точке (2 ; — 3)?

Помогите пожалуйста найдите радиус окружности, если она проходит через точку ( — 2 ; 1) и ее центр находится в точке (2 ; — 3).

Окружность с центром в точке A(3 ; –6) проходит через точку М(1 ; –1)?

Окружность с центром в точке A(3 ; –6) проходит через точку М(1 ; –1).

Чему равен радиус этой окружности?

Напишите уравнение окружности радиусом 5, которое проходит через точку (2, 5), если его центр находится на биссектрисе первого координатной четверти?

Напишите уравнение окружности радиусом 5, которое проходит через точку (2, 5), если его центр находится на биссектрисе первого координатной четверти.

На странице вопроса Найдите радиус окружности, если она проходит через точку ( — 2 ; 1) и ее центр находится в точке (2 ; — 3)? из категории Геометрия вы найдете ответ для уровня учащихся 5 — 9 классов. Если полученный ответ не устраивает и нужно расшить круг поиска, используйте удобную поисковую систему сайта. Можно также ознакомиться с похожими вопросами и ответами других пользователей в этой же категории или создать новый вопрос. Возможно, вам будет полезной информация, оставленная пользователями в комментариях, где можно обсудить тему с помощью обратной связи.

Y = x³ — 3x² / 3 — x ООФ : x≠3 y = x²(x — 3 / — (x — 3) = — x² , (x≠3) y = — x² , (x≠3) график парабола c вершиной в начале координат , ветвикоторой направлены вниз ; выколотая точка параболы сабсциссой x = 3.

Сторона ромба = √24 ^ 2 + 7 ^ 2 = √576 + 49 = √625 = 25 Ответ : 25.

Вот. Стороны равны Там теорема Пифагора и все рассписано.

X + x + x + 33 = 180 3x = 180 — 33 3x = 147 x = 49 49 и 49 — углы при основании 49 + 33 = 82 — угол при вершине.

Смотри во вложении.

По условию АВСD прямоугольник : АВ = 2 см, ВС = 1 см. 1) АВСD вращается вокруг АВ ; образуется цилиндр. Радиус которого ВС = 1см ; высота СD = АВ = 2 см. Площадь боковой поверхности равна S1 = 2πrh = 2·1·2π = 4π см². S1 = 4π см². 2) АВСD вращает..

№1 S бок = 5 * 8 * 16 = 640 S пол я не могу найти.

В равнобедренном треугольнике ABC AB = BC = 11 AC = 14 найти расстояние от вершины B до а) точки M пересечения медиан б) точки О1 пересечения биссектрис в) точки О пересечения серединных перпендикуляров сторон г) точки H пересечения высот.

1. Объём находится по формуле : где S — площадь основания (круга), а h — высота конуса. 2. 3. Ответ : V = 4π /.

Четырехугольник может быть вписан в окружность только при условии что сумма противоположных углов равна 180 градусов. Т. е. 180 — 66 = 114 и 180 — 73 = 107.

Радиус — что это такое и как найти радиус окружности

Через длину стороны

Формула для нахождения длины окружности через радиус:

, где r — радиус окружности.

Найти радиус круга, зная окружность

Окружность круга PРезультат

Радиус и диаметр

Радиус в математике всегда обозначается латинской буквой «R» или «r». Принципиальной разницы, большую букву писать или маленькую, нет.

А два соединенных вместе радиуса, которые к тому же находятся на одной прямой, называются диаметром. Или по-другому:

Диаметр – это отрезок, который проходит через центр окружности и соединяет две противоположные точки на ее поверхности. По аналогии с радиусом под диаметром подразумевают и длину этого отрезка.

Обозначается диаметр также первой буквой своего слова – D или d.

Исходя из определения диаметра, можно сделать простой вывод, который одновременно является одной из базовых основ геометрии.

Длина диаметра равна удвоенной длине радиуса.

Вычисление радиуса

Радиус можно посчитать разными способами.

Если известен диаметр

Этот способ самый простой. Диаметр равен двум радиусам. Поэтому радиус будет высчитываться по формуле r=d/2.

Если известна длина окружности круга

Также несложно будет узнать радиус, если известна длина окружности круга. Формула для расчета длины окружности C=2πr, в которой C является длиной окружности, π=3,14, а r — это как раз искомый радиус.

Преобразовав данную формулу, получим: r=C/2π. Вообще, число «Пи» в формуле — это постоянное значение, округленное до 3,14. На самом деле «Пи» выглядит так:

Означает данное значение отношение длины окружности к диаметру той же окружности.

Если известна площадь круга

Формула площади круга выглядит так: A= π(r²). Эту формулу можно преобразовать в формулу радиуса:

В ней A — это площадь круга, число «Пи» мы уже знаем, оно равно округленно 3,14, а r — это и есть искомое значение радиуса.

Как найти радиус круга, все школьники учат на геометрии. Взрослые, конечно, со временем забывают эти формулы. Но, прочитав данную статью, радиус круга может найти каждый: и взрослый, и ребенок.

Способ расчета радиуса круга:

Круг (окружность) – геометрическая фигура на плоскости, все точки которой равноудалены от данной точки (центр круга).
Формула радиуса круга:
где P – длина окружности, pi – число π, равное примерно 3.14

Круг (окружность) – геометрическая фигура на плоскости, все точки которой равноудалены от данной точки (центр круга).
Формула радиуса круга:
где S – площадь круга, pi – число π, равное примерно 3.14

Через сторону описанного квадрата

Сторона описанного квадрата равна диаметру окружности. А диаметр — повторимся — равен двум радиусам. Поэтому разделите сторону квадрата на два.

• r — искомый радиус окружности.
• a — сторона описанного квадрата.

Как посчитать радиус зная длину окружности

Чему равен радиус (r) если длина окружности C?

Формула

r = C /_2π , где π ≈ 3.14

Свойства радиуса

В отношении радиуса действуют несколько важных правил:

1. Радиус составляет половину диаметра. Это мы продемонстрировали только что.
2. У окружности может быть сколько угодно радиусов. Но все они будут равны по длине между собой.

Радиус, который перпендикулярен хорде, делит ее на две равные части.

Напомним, хордой называется любой отрезок, который проходит через две точки на поверхности окружности, но не через центр. Этим она принципиально отличается от диаметра.

По площади сектора и центральному углу

• Например, если площадь сектора равна 50 см 2 , а центральный угол равен 120 градусов, формула запишется следующим образом: .

Площадь сегмента

Рассмотрим круговой сегмент, изображённый на рисунке 5, и обозначим его площадь символом S (α), где буквой α обозначена величина соответствующего центрального угла .

Поскольку площадь сегмента равна разности площадей кругового сектора MON и треугольника MON (рис.5), то в случае, когда величина α выражена в градусах , получаем

В случае, когда величина α выражена в в радианах , получаем

Формулы для площади круга и его частей

,

где R – радиус круга, D – диаметр круга

,

если величина угла α выражена в радианах

,

если величина угла α выражена в градусах

,

если величина угла α выражена в радианах

,

если величина угла α выражена в градусах

Числовая характеристика	Рисунок	Формула
Площадь круга
Площадь сектора
		Площадь сегмента

Площадь круга

,

где R – радиус круга, D – диаметр круга

Площадь сектора

,

если величина угла α выражена в радианах

,

если величина угла α выражена в градусах

Площадь сегмента

,

если величина угла α выражена в радианах

,

если величина угла α выражена в градусах

Центральный угол, вписанный угол и их свойства

Связанные определения

• Центральный угол в окружности — это угол , образованный двумя радиусами.
• Радиус кривизны кривой — это радиус окружности, имеющей с этой кривой касание второго порядка.

Примеры задач

Задание 1
Длина окружности равняется 87,92 см. Найдите ее радиус.

Решение:
Используем первую формулу (через периметр):

Задание 2
Найдите радиус круга, если его площадь составляет 254,34 см 2 .

Решение:
Воспользуемся формулой, выраженной через площадь фигуры:

Длина дуги

Рассмотрим дугу окружности, изображённую на рисунке 3, и обозначим её длину символом L(α), где буквой α обозначена величина соответствующего центрального угла .

В случае, когда величина α выражена в градусах , справедлива пропорция

из которой вытекает равенство:

В случае, когда величина α выражена в радианах , справедлива пропорция

из которой вытекает равенство:

Уравнение окружности

r 2 = ( x – a ) 2 + ( y – b ) 2

3. Параметрическое уравнение окружности с радиусом r и центром в точке с координатами ( a, b ) в декартовой системе координат:

<	x = a + r cos t
	y = b + r sin t

Углы между двумя хордами

Случай 1: два секущие пересекаются внутри окружности.

Когда две секущие пересекаются внутри окружности, величина образованных угла, в два раза меньше суммы величин дуг, на которые они опираются. На рисунке дуга AB и дуга CD равны 60° и 50° тогда углы 1 и 2 равны Случай 2: две секущие пересекаются вне окружности.

Иногда секущие пересекаются за пределами окружности. Когда это случается, величина образующихся углов равна половине разности дуг, на которые они опираются.

Через площадь и полупериметр описанного треугольника

Разделите площадь описанного треугольника на его полупериметр.

• r — искомый радиус окружности.
• S — площадь треугольника.
• p — полупериметр треугольника (равен половине от суммы всех сторон).

Основные свойства касательных к окружности

3. Если две касательные, с точками соприкосновения B и C, на одной окружности не параллельны, то они пересекаются в точке A, а отрезок между точкой соприкосновения и точкой пересечения одной касательной равен таком же отрезке на другой касательной:

Также, если провести прямую через центр окружности О и точку пересечения A этих касательных, то углы образованный между этой прямой и касательными будут равны:

Обобщения

Радиусом множества , лежащего в метрическом пространстве с метрикой , называется величина . Например, радиус n-размерного гиперкуба со стороной s равен

Через диагональ вписанного прямоугольника

Диагональ прямоугольника является диаметром окружности, в которую он вписан. А диаметр, как мы уже вспомнили, в два раза больше радиуса. Поэтому достаточно разделить диагональ на два.

• R — искомый радиус окружности.
• d — диагональ вписанного прямоугольника. Напомним, она делит фигуру на два прямоугольных треугольника и является их гипотенузой — стороной, лежащей напротив прямого угла. Поэтому, если диагональ неизвестна, её можно найти через соседние стороны прямоугольника с помощью теоремы Пифагора.
• a, b — стороны вписанного прямоугольника.

Площадь круга, онлайн расчет

Как найти площадь круга по формуле через радиус либо диаметр круга.Площадь круга, онлайн расчет

Вместо заключения

Чтобы еще больше понять, насколько важно понятие РАДИУС, вспомните инструмент, с помощью которого можно начертить окружность. Это циркуль и выглядит он вот так.

Пользоваться им просто. Ножка с острым концом ставится в центр будущей окружности. А ножка с грифелем прочерчивает линию. А расстояние, на котором они будут друг от друга, и есть РАДИУС.

Найти центр и радиус окружности

Если окружность задана уравнением вида

найти центр (a;b) и радиус R такой окружности несложно.

Определить по уравнению окружности координаты её центра и радиуса:

Таким образом, центр данной окружности — точка (3;7), радиус R=2.

a=-2, b=5, R²=1. Окружность с центром в точке (-2;5) и радиусом 1.

Центр окружности — (0;-3), радиус R=3.

Центр — в точке (6;0), радиус R=√5.

Это уравнение задаёт окружность с центром в начале координат. Центр — O(0;0), радиус R=√11.

Чтобы найти центр и радиус окружности, заданной уравнением вида

нужно дополнить его до полных квадратов, чтобы привести к привычному виду.

Для этого сначала сгруппируем слагаемые

затем прибавим и вычтем квадрат второго слагаемого из формулы квадрата разности (2ax- удвоенное произведение первого слагаемого на второе. Первое — x, второе — a)

При a²+b²-c>0 это уравнение задаёт окружность с радиусом

При a²+b²-c=0 уравнению удовлетворяют координаты единственной точки (a;b).

При a²+b²-c

Выделяем в уравнении полные квадраты. В первых скобках удвоенное слагаемое 10x представляем как 10x=2·a·5 (чтобы получить 2ab для формулы a²+2ab+b²=(a+b)²). Получается, что b=5. Если прибавить и вычесть b², результат не изменится:

Центром этой окружности является точка (-5;3), радиус R=7.

Центр окружности — точка (2,5;0), радиус R=1,5.