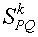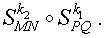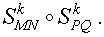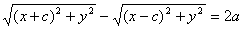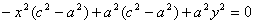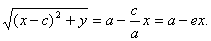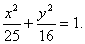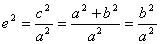Сжатие окружности с коэффициентом 2

Преобразования плоскости

Движения плоскости

Теорема Шаля

Афинные преобразования плоскости

Классификация афинных преобразований плоскости

Видео:Преобразование графиков функций. Сжатие и растяжение. 10 класс.Скачать

Преобразования плоскости

Определение 1 . Преобразованием плоскости называют правило, с помощью которого каждой точке плоскости ставится в соответствие точка этой же плоскости.

Из определения 1 вытекает, что, если F – преобразование плоскости α , а M – произвольная точка плоскости , то F(M) тоже является точкой плоскости α .

Определение 2 . Точку F(M) называют образом точки M при преобразовании F , а точку M называют прообразом точки F(M) при преобразовании F.

Аналогично определяются образы и прообразы любых фигур на плоскости при преобразовании F.

Определение 3 . Преобразование плоскости называют взаимно однозначным преобразованием плоскости на себя , если разные точки имеют разные образы, и каждая точка плоскости имеет прообраз.

Другими словами, при взаимно однозначном преобразовании плоскости на себя разные точки плоскости переходят в разные точки этой же плоскости, и в каждую точку плоскости переходит какая-то точка этой плоскости.

Определение 4 . Произведением (композицией) двух преобразований называют преобразование, которое получается в результате последовательного выполнения этих преобразований.

Таким образом, если F и G – два преобразования, то произведением этих преобразований будет такое преобразование H, которое произвольную точку A плоскости переводит в точку A’ этой плоскости, определяемую по формуле:

Видео:Сдвиг, растяжение, сжатие графика функцииСкачать

Движения плоскости

Определение 5 . Движением плоскости называют такое преобразование плоскости, при котором расстояние между двумя любыми точками плоскости равно расстоянию между их образами.

Следующие преобразования являются движениями плоскости:

1. Параллельный перенос (сдвиг) на заданный вектор

При параллельном переносе плоскости на заданный вектор 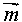(рис.1) произвольная точка A плоскости переходит в такую точку A’ плоскости, что выполнено равенство

Замечание . Движение, при котором каждая точка плоскости остаётся на своём месте, называют тождественным преобразованием . Тождественное преобразование можно рассматривать как параллельный перенос на вектор, равный нулю.

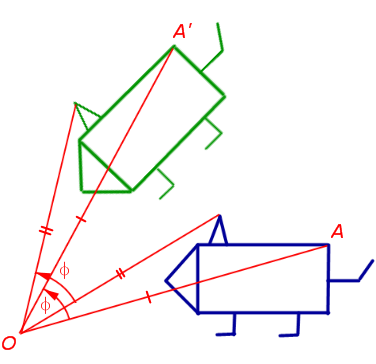
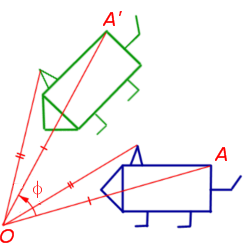
2. Поворот вокруг заданной точки, называемой центром поворота, на заданный угол

При повороте плоскости вокруг точки O на угол φ (рис. 2) произвольная точка A плоскости переходит в такую точку A’ плоскости, что выполнены равенства

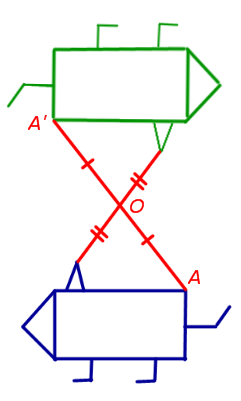
3. Центральная симметрия (симметрия относительно заданной точки, называемой центром симметрии)

При центральной симметрии плоскости относительно точки O произвольная точка A плоскости переходит в такую точку A’ плоскости, что серединой отрезка AA’ является точка O – заданный центр симметрии (рис.3).

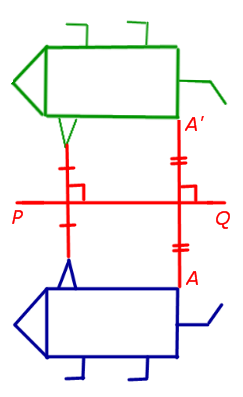
4. Осевая симметрия (симметрия относительно заданной прямой, называемой осью симметрии)

При осевой симметрии относительно прямой PQ ( ось симметрии ) произвольная точка A плоскости переходит в такую точку A’ плоскости, что, во-первых, прямая AA’ перпендикулярна прямой PQ , а, во-вторых, точка пересечения прямых AA’ и PQ является серединой отрезка AA’

5. Скользящая симметрия (композиция осевой симметрии относительно заданной прямой и параллельного переноса на заданный отличный от нуля вектор, параллельный этой прямой)

Если прямая PQ – ось симметрии, а параллельный перенос задаётся вектором 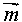параллельным прямой PQ , то результат скользящей симметрии можно условно изобразить так, как показано на рисунке 5.

Видео:Математика без Ху!ни. Кривые второго порядка. Эллипс.Скачать

Движения плоскости, сохраняющие ориентацию. Движения плоскости, изменяющие ориентацию. Теорема Шаля

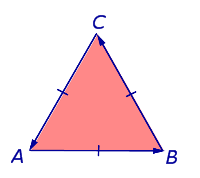
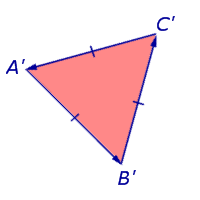
Рассмотрим на плоскости произвольный равносторонний треугольник и обозначим его вершины буквами A, B и C так, чтобы при обходе по сторонам треугольника в направлении

треугольник оказывался расположенным слева (рис.6). При таком обозначении вершин обход треугольника будет осуществляться против часовой стрелки.

Предположим теперь, что некоторое движение F переводит треугольник ABC в треугольник A’B’C’, у которого

Поскольку каждое движение плоскости сохраняет расстояния между точками, то треугольник A’B’C’ также будет равносторонним, однако возможны следующие два случая.

В первом случае при обходе по сторонам треугольника A’B’C’ в направлении

треугольник A’B’C’ располагается слева, и обход производится против часовой стрелки (рис.7).

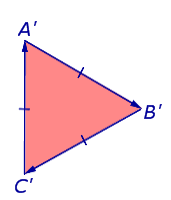
Во втором случае при обходе по сторонам треугольника A’B’C’ в направлении

треугольник A’B’C’ располагается справа, и обход производится по часовой стрелке (рис.8).

Определение 6 . Если при движении F осуществляется первый случай, то такое движение называют движением, сохраняющим ориентацию плоскости ( движением 1-го рода, собственным движением ). Если при движении F осуществляется второй случай, то такое движение называют движением, изменяющим ориентацию ( движением 2-го рода, несобственным движением ).

Классификацию всех движений плоскости даёт следующая теорема Шаля.

Теорема Шаля . Любое движение плоскости, сохраняющее ориентацию, является или параллельным переносом, или поворотом. Любое движение плоскости, изменяющее ориентацию, является или осевой симметрией, или скользящей симметрией.

Видео:Аналитическая геометрия: Эллипс, Парабола, Гипербола. Высшая математикаСкачать

Аффинные преобразования плоскости

Определение 7 . Аффинным преобразованием плоскости называют такое взаимно однозначное преобразование плоскости на себя, при котором образом любой прямой на плоскости является прямая.

Поскольку каждое движение плоскости переводит прямые линии в прямые линии, то каждое движение является аффинным преобразованием.

Однако аффинные преобразования не ограничиваются движениями плоскости. Следующие преобразования также являются аффинными преобразованиями плоскости:

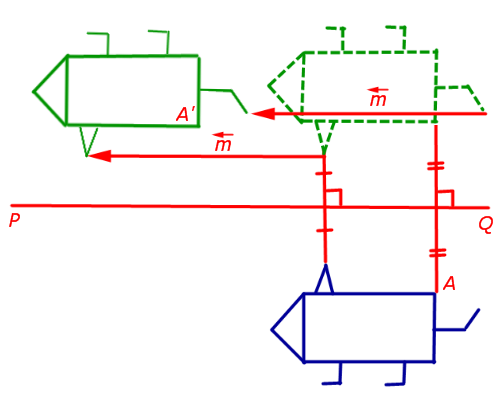
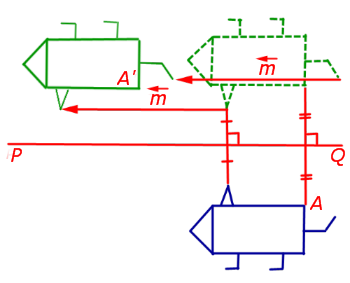
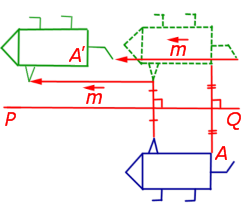
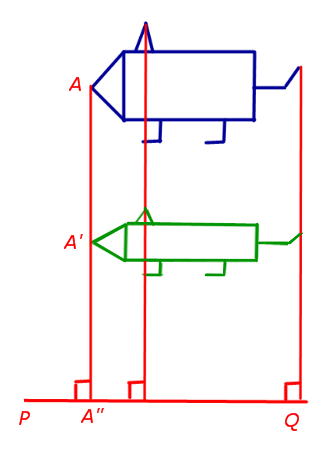
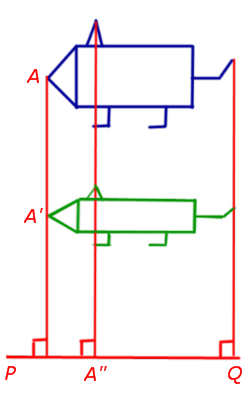
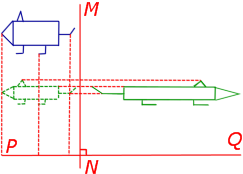
1. Сжатие (растяжение) к прямой с заданным коэффициентом сжатия (растяжения)

При сжатии (растяжении) плоскости к прямой PQ с заданным коэффициентом сжатия k (рис.9) произвольная точка A плоскости переходит в такую точку A’ плоскости, что выполнены следующие условия:

• прямая AA’ перпендикулярна прямой PQ ;
• если обозначить буквой A» точку пересечения прямых AA’ и PQ , то будет справедливо равенство

Замечание 1 . В случае, когда | k | , рассматриваемое аффинное преобразование называют сжатием к прямой PQ , если же | k | > 1 , то это преобразование называют растяжением .

Замечание 2 . Будем использовать для рассматриваемого сжатия (растяжения) обозначение

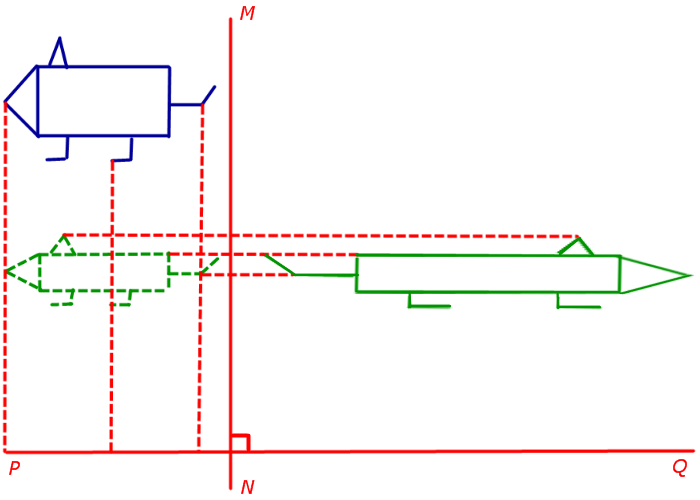
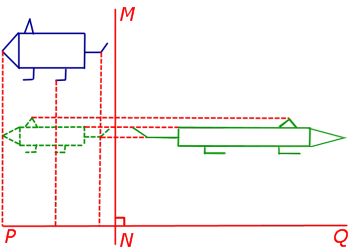
2. Сжатие (растяжение) по двум заданным взаимно перпендикулярным направлениям с заданными коэффициентами сжатия (растяжения)

Пусть PQ и MN – две взаимно перпендикулярных прямых, а числа k₁ и k₂ – коэффициенты сжатия (расширения) плоскости в направлении прямых PQ и MN соответственно. Тогда сжатием (растяжением) по двум заданным взаимно перпендикулярным направлениям PQ и MN с коэффициентами k₁ и k₂ (рис.10) называют композицию сжатий (растяжений).

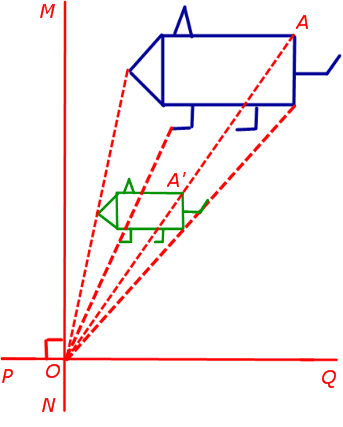
3. Гомотетия с заданным центром гомотетии и заданным коэффициентом сжатия (растяжения)

Гомотетией с центром в точке O и коэффициентом k называют такое аффинное преобразование, при котором произвольная точка A плоскости переходит в такую точку A’ плоскости, что выполнены следующие условия:

• точка A’ лежит на прямой AO ;
• справедливо равенство

Замечание . Рассмотрим две произвольных взаимно перпендикулярных прямых PQ и MN, пересекающихся в точке O. Тогда гомотетия с центром в точке O и коэффициентом k совпадёт со сжатием (растяжением) по направлениям PQ и MN с коэффициентами, равными k . Другими словами, гомотетия является композицией сжатий (растяжений):

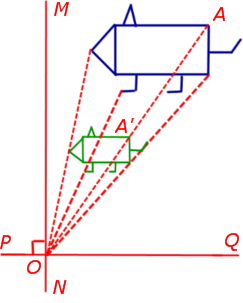
4. Преобразование подобия с заданным коэффициентом подобия

Преобразованием подобия с коэффициентом подобия k называют аффинное преобразование, представленное в виде композиции гомотетии с коэффициентом k и движения (рис. 12).

Видео:Построение графиков тригонометрических функций с помощью преобразований. Практ. часть. 10 класс.Скачать

Классификация аффинных преобразований плоскости

Справедлива следующая теорема о классификации аффинных преобразований плоскости.

Видео:Преобразование графиков функций. Растяжение, сжатие, параллельный перенос…Скачать

Сжатие окружности с коэффициентом 2

Ах 2 + 2Вху + Су 2 + 2 Dx + 2 Ey + F = 0.

Существует система координат (не обязательно декартова прямоугольная), в которой данное уравнение может быть представлено в одном из видов, приведенных ниже.

1) — уравнение эллипса.

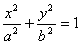
2) — уравнение “мнимого” эллипса.

3) — уравнение гиперболы.

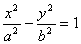
4) a 2 x 2 – c 2 y 2 = 0 – уравнение двух пересекающихся прямых.

5) y 2 = 2 px – уравнение параболы.

6) y 2 – a 2 = 0 – уравнение двух параллельных прямых.

7) y 2 + a 2 = 0 – уравнение двух “мнимых” параллельных прямых.

8) y 2 = 0 – пара совпадающих прямых.

9) ( x – a ) 2 + ( y – b ) 2 = R 2 – уравнение окружности.

В окружности ( x – a ) 2 + ( y – b ) 2 = R 2 центр имеет координаты ( a ; b ).

Пример. Найти координаты центра и радиус окружности, если ее уравнение задано в виде:

2 x 2 + 2 y 2 – 8 x + 5 y – 4 = 0.

Для нахождения координат центра и радиуса окружности данное уравнение необходимо привести к виду, указанному выше в п.9. Для этого выделим полные квадраты:

x 2 + y 2 – 4 x + 2,5 y – 2 = 0

x 2 – 4 x + 4 –4 + y 2 + 2,5 y + 25/16 – 25/16 – 2 = 0

( x – 2) 2 + ( y + 5/4) 2 – 25/16 – 6 = 0

( x – 2) 2 + ( y + 5/4) 2 = 121/16

Отсюда находим О (2; -5/4); R = 11/4.

Определение. Эллипсом называется линия, заданная уравнением .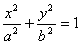

О пределение. Фокусами называются такие две точки, сумма расстояний от которых до любой точки эллипса есть постоянная величина.

у

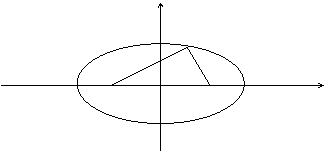
с – половина расстояния между фокусами;

a – большая полуось;

b – малая полуось.

Теорема. Фокусное расстояние и полуоси эллипса связаны соотношением:

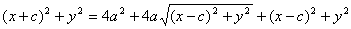
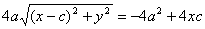
Доказательство: В случае , если точка М находится на пересечении эллипса с вертикальной осью, r ₁ + r ₂ = 2 (по теореме Пифагора). В случае , если точка М находится на пересечении эллипса с горизонтальной осью, r ₁ + r ₂ = a – c + a + c . Т.к. по определению сумма r ₁ + r ₂ – постоянная величина, то , приравнивая, получаем:

a 2 = b 2 + c 2

Определение. Форма эллипса определяется характеристикой, которая является отношением фокусного расстояния к большей оси и называется эксцентриситетом.

Определение. Величина k = b / a называется коэффициентом сжатия эллипса, а величина 1 – k = ( a – b )/ a называется сжатием эллипса.

Коэффициент сжатия и эксцентриситет связаны соотношением: k 2 = 1 – e 2 .

Если a = b ( c = 0, e = 0, фокусы сливаются), то эллипс превращается в окружность.

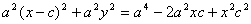
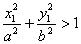
Если для точки М( х₁, у₁) выполняется условие: , то она находится внутри эллипса, а если , то точка находится вне эллипса.

Теорема. Для произвольной точки М( х , у), принадлежащей эллипсу верны соотношения:

r ₁ = a – ex , r ₂ = a + ex .

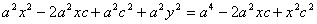
Доказательство. Выше было показано, что r ₁ + r ₂ = 2 a . Кроме того, из геометрических соображений можно записать:

После возведения в квадрат и приведения подобных слагаемых:

Аналогично доказывается, что r ₂ = a + ex . Теорема доказана.

С эллипсом связаны две прямые, называемые директрисами. Их уравнения:

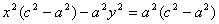
x = a / e ; x = — a / e .

Теорема. Для того , чтобы точка лежала на эллипсе, необходимо и достаточно, чтобы отношение расстояния до фокуса к расстоянию до соответствующей директрисы равнялось эксцентриситету е.

Пример. Составить уравнение прямой, проходящей через левый фокус и нижнюю вершину эллипса, заданного уравнением:

1) Координаты нижней вершины: x = 0; y 2 = 16; y = -4.

2) Координаты левого фокуса: c 2 = a 2 – b 2 = 25 – 16 = 9; c = 3; F ₂ (-3; 0).

3) Уравнение прямой, проходящей через две точки:

Пример. Составить уравнение эллипса, если его фокусы F ₁ (0; 0), F ₂ (1; 1), большая ось равна 2.

Уравнение эллипса имеет вид: 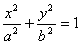. Расстояние между фокусами:

2 c = , таким образом, a 2 – b 2 = c 2 = ½

по условию 2а = 2, следовательно а = 1, b =

Итого: .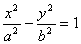

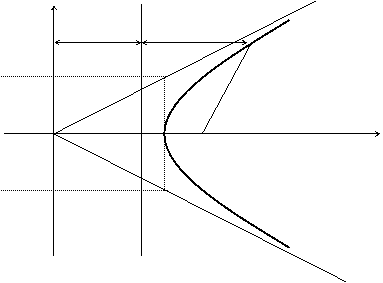
Определение. Гиперболой называется множество точек плоскости, для которых модуль разности расстояний от двух данных точек, называемых фокусами есть величина постоянная, меньшая расстояния между фокусами.

y

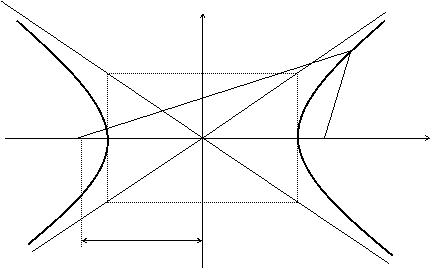
По определению ï r ₁ – r ₂ ï = 2 a . F ₁ , F ₂ – фокусы гиперболы. F ₁ F ₂ = 2 c .

Выберем на гиперболе произвольную точку М( х , у). Тогда :

обозначим с 2 – а 2 = b 2 (геометрически эта величина – меньшая полуось)

Получили каноническое уравнение гиперболы.

Гипербола симметрична относительно середины отрезка, соединяющего фокусы и относительно осей координат.

Ось 2а называется действительной осью гиперболы.

Ось 2 b называется мнимой осью гиперболы.

Гипербола имеет две асимптоты, уравнения которых

Определение. Отношение 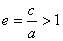называется эксцентриситетом гиперболы, где с – половина расстояния между фокусами, а – действительная полуось.

С учетом того, что с 2 – а 2 = b 2 :

Если а = b , e = , то гипербола называется равнобочной (равносторонней).

Определение. Две прямые, перпендикулярные действительной оси гиперболы и расположенные симметрично относительно центра на расстоянии a / e от него, называются директрисами гиперболы. Их уравнения: .

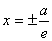
Теорема. Если r – расстояние от произвольной точки М гиперболы до какого — либо фокуса, d – расстояние от той же точки до соответствующей этому фокусу директрисы, то отношение r / d – величина постоянная, равная эксцентриситету.

Доказательство. Изобразим схематично гиперболу.

y

Видео:Подобие треугольников. Признаки подобия треугольников (часть 1) | МатематикаСкачать

Растяжение и сжатие графиков функций

Список функций, изученных в 7 и 8 классе

Растяжение и сжатие графика по оси OX

Сравним графики пар функций, которые в общем виде можно записать так:

$$ y_1 = f(x), y_2 = f(px) $$

где $p gt 1$, произвольный положительный множитель.

$ y_2 = f(2x) = (2x)^2 = 4x^2 $

$y_2 = y_1 при x_2 = frac x_1$

График сжимается в 2 раза по оси OX

$ y_2 = y_1 при x_2 = frac x_1 $

График сжимается в 2 раза по оси OX

$y_2=y_1 при x_2 = frac x_1$

График сжимается в 2 раза по оси OX

Теперь сравним пары функций с делением на p:

$$ y_1 = f(x), quad y_2 = f left( frac

right), quad p gt 1 $$

$ y_2 = f left(fracright) = left(fracright)^2 = frac $

$y_2 = y_1 при x_2 = 2x_1$

График растягивается в 2 раза по оси OX

$y_2 = f left(fracright) = frac = frac$

$ y_2 = y_1 при x_2 = 2x_1$

График растягивается в 2 раза по оси OX

$y_2=y_1 при x_2 = 2x_1$

График растягивается в 2 раза по оси OX

При сравнении графиков двух функций

$$ y_1 = f(x), quad y_2 = f(px), quad p gt 1 $$

график второй функции сжимается в p раз по оси OX по сравнению с графиком первой функции.

При сравнении графиков двух функций

$$ y_1 = f(x), quad y_2 = f Biggl(frac

Biggr), quad p gt 1 $$

график второй функции растягивается в p раз по оси OX по сравнению с графиком первой функции.

Заметим, что данные утверждения справедливы не только для рассмотренных функций, но и для любых других (синусов, косинусов, логарифмов и т.п.)

Растяжение и сжатие графика по оси OY

Сравним графики пар функций, которые в общем виде можно записать так:

$$ y_1 = f(x), quad y_2 = Af(x) $$

где $A gt 1$, произвольный положительный множитель.

$y_2 = 2y_1 при x_2 = x_1$

График растягивается в 2 раза по оси OY

$ y_2 = 2y_1 при x_2 = x_1$

График растягивается в 2 раза по оси OY

$y_2 = 2f(x) = 2sqrt$

$y_2 = 2y_1 при x_2 = x_1$

График растягивается в 2 раза по оси OY

Теперь сравним пары функций с делением на A:

$y_2 = fracy_1 при x_2 = x_1$

График сжимается в 2 раза по оси OY

$ y_2 = fracy_1 при x_2 = x_1$

График сжимается в 2 раза по оси OY

$y_2 = fracy_1 при x_2 = x_1$

График сжимается в 2 раза по оси OY

При сравнении графиков двух функций

$$ y_1 = f(x), quad y_2 = Af(x), quad A gt 1 $$

график второй функции растягивается в A раз по оси OY по сравнению с графиком первой функции.

При сравнении графиков двух функций

график второй функции сжимается в A раз по оси OY по сравнению с графиком первой функции.

Заметим, что данные утверждения справедливы не только для рассмотренных функций, но и для любых других (синусов, косинусов, логарифмов и т.п.)

Примеры

Пример 1. Постройте в одной координатной плоскости графики функций:

По сравнению с графиком $y = sqrt$:

• график функции $y = sqrt$ сжимается в 3 раза по оси OX(←)
• график функции $y = sqrt<frac>$ растягивается в 3 раза по оси OX(→)
• график функции $y = 3sqrt$ растягивается в 3 раза по оси OY(↑)

Пример 2*. Постройте в одной координатной плоскости графики функций:

$$ y = f(x), y = f(2x), y = f Biggl(fracBiggr), y = 2f(x) $$

Исходная функция $y = f(x) = x^2+3x+2$

$$ y = f(2x) = (2x)^2+3 cdot (2x)+2 = 4x^2+6x+2 $$

$$ y = fBiggl(fracBiggr) = Biggl(fracBiggr)^2+3 cdot Biggl(fracBiggr) +2 = frac+ frac x+2 $$

По сравнению с графиком $y = f(x) = x^2+3x+2$:

• график функции y = f(2x) сжимается в 2 раза по оси OX(→)
• график функции $y = f left(fracright)$ растягивается в 2 раза по оси OX(←)
• график функции y = 2f(x) растягивается в 2 раза по оси OY(↑)

📺 Видео

Реакция на результаты ЕГЭ 2022 по русскому языкуСкачать

9 класс, 6 урок, Уравнение окружностиСкачать

Графики функций №6.Сжатие графика вдоль осейСкачать

Уравнение окружностиСкачать

Математика | 5 ЗАДАЧ НА ТЕМУ ОКРУЖНОСТИ. Касательная к окружности задачиСкачать

Урок 100 (осн). Коэффициенты линейного и объемного расширения телСкачать

12 Преобразования графиков. y=kf(x) и y=f(kx)Скачать

Математика без Ху!ни. Уравнение плоскости.Скачать

Найти центр и радиус окружностиСкачать

ГЕОМЕТРИЯ 9 класс: Уравнение окружности и прямойСкачать

СЛОЖИТЕ ДВА КОРНЯСкачать

Геометрические преобразования графиков функций. Растяжение, сжатие и симметрия относительно оси ОХСкачать

ГРАФИК ФУНКЦИЙ — Сдвиги Графика Функции, Как строить Графики Функции // Алгебра 8 классСкачать