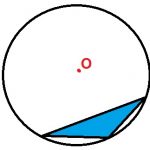
Укажите номера верных утверждений центр описанной около треугольника окружности (8 видео)

Укажите номера верных утверждений центр описанной около треугольника окружности

Задание 20. Какое из следующих утверждений верно?

1) Центр описанной около треугольника окружности лежит внутри треугольника.

2) Основания равнобедренной трапеции равны.

3) Все высоты равностороннего треугольника равны.

1) Не обязательно, есть тупоугольные треугольники, у которых центр описанной окружности вне его.

2) Нет, они могут быть и разными.

3) Да, у равностороннего треугольника все высоты равны.

Содержание

Решение №2110 Какое из следующих утверждений верно? 1) Центр описанной около треугольника окружности всегда лежит внутри этого треугольника.
Укажите номера верных утверждений?
Центр описанной около треугольника окружности симметричен центру вписанной в него окружности относительно одной из сторон?
Укажите номера верных утверждений?
В5. Укажите в ответе номера верных утверждений?
13. Какие из следующих утверждений верны?
Докажите, что если центр окружности, описанной около треугольника , принадлежит его стороне , то этот треугольник прямоугольный?
Укажите номера верных утверждений : 1) Центром описанной окружности треугольника является точка пересечения его высот 2)центром описанной окружности треугольника является точка пересечения его медиан ?
Укажите номера верных утверждений?
Верны ли утверждения : 1 центром окружности описанной околотреугольника , являестся точка пересечения его биссектрис?
Правильно ли?
Какие из следующих утверждений верны?
🔥 Видео

Видео:ОГЭ 2019. Задание 17. Разбор задач. Геометрия. Окружность.Скачать

Решение №2110 Какое из следующих утверждений верно? 1) Центр описанной около треугольника окружности всегда лежит внутри этого треугольника.

Какое из следующих утверждений верно?

1) Центр описанной около треугольника окружности всегда лежит внутри этого треугольника.
2) Сумма углов равнобедренного треугольника равна 180 градусам.
3) Диагонали ромба равны.

В ответ запишите номер выбранного утверждении.

Источник: ОГЭ Ященко 2022 (36 вар)

1) не верно , ниже пример, когда центр окружности лежит вне треугольника:

2) верно , сумма углов любого треугольника равна 180 градусов;
3) не верно , ниже пример, ромба с не равными диагоналями:

Видео:Окружность вписанная в треугольник и описанная около треугольника.Скачать

Укажите номера верных утверждений?

Геометрия | 5 — 9 классы

Укажите номера верных утверждений.

1) Центром окружности, вписанной в правильный треугольник, является точка пересечения серединных перпендикуляров к его сторонам.

2) В любой прямоугольный треугольник можно вписать окружность.

3) Центр окружности, описанной около прямоугольного треугольника, находится на катете этого треугольника.

4) Центром окружности, описанной около правильного треугольника, является точка пересечения его высот.

5) Квадрат любой стороны треугольника равен сумме квадратов двух других сторон без произведения этих сторон на косинус угла между ними.

1 — верно, так какцентром окружности, вписанной в любой треугольник, является точка пересечения биссектрис его внутренних углов, а в правильном треугольнике его биссектрисы являются и высотами (серединные перпендикуляры) и медианами.

2 верно, так как в любой треугольник можно вписать окружность и при том только одну.

4 верно, так как центром окружности, описанной около треугольника, является точка пересечения серединных перпендикуляров к его сторонам, а в правильном треугольникеего высоты являются серединными перпендикулярами (так как являются и медианами).

3 — неверно, так как центр окружности, описанной около прямоугольного треугольника, находится на гипотенузе этого треугольника.

4 — верно, так как центром окружности, описанной около любого треугольника, является точка пересечения серединных перпендикуляров, а в правильном треугольнике высоты являются срединными перпендикулярами.

5 — неверно, так как квадрат любой стороны треугольника равен сумме квадратов двух

других сторон без УДВОЕННОГО произведения этих сторон на косинус угла между ними.

Видео:Радиус описанной окружностиСкачать

Центр описанной около треугольника окружности симметричен центру вписанной в него окружности относительно одной из сторон?

Центр описанной около треугольника окружности симметричен центру вписанной в него окружности относительно одной из сторон.

Найдите углы треугольника.

Видео:Геометрия 9 класс. Радиус описанной и вписанной окружности треугольника. Формулы радиуса.Скачать

Укажите номера верных утверждений?

Укажите номера верных утверждений.

1) Медианы треугольника пересекаются в одной точке.

2) Центр вписанной в равнобедренный треугольник окружности лежит на пересечении серединных перпендикуляров.

3) Если точка О лежит на биссектрисе угла А, то расстояние от точки О до сторон угла равны.

4) Точка, лежащая на высоте треугольника, может быть центром описанной окружности.

Видео:Окружность описана около равнобедренного треугольника. Найти центральный уголСкачать

В5. Укажите в ответе номера верных утверждений?

В5. Укажите в ответе номера верных утверждений.

1. Центром окружности, вписанной в правильный треугольник, является точка пересечения серединных перпендикуляров к его сторонам.

2. В любой прямоугольный треугольник можно вписать окружность.

3. Центр окружности, описанной около прямоугольного треугольника, находится на катете этого треугольника.

Видео:найти радиус окружности, описанной вокруг треугольникаСкачать

13. Какие из следующих утверждений верны?

1. Если при пересечении двух прямых третьей прямой внутренние накрест лежащие углы равны 90°, то эти две прямые параллельны.

2. В любой четырёхугольник можно вписать окружность.

3. Центром окружности, описанной около треугольника, является точка пересечения серединных перпендикуляров к сторонам треугольника.

Видео:Построить описанную окружность (Задача 1)Скачать

Докажите, что если центр окружности, описанной около треугольника , принадлежит его стороне , то этот треугольник прямоугольный?

Докажите, что если центр окружности, описанной около треугольника , принадлежит его стороне , то этот треугольник прямоугольный.

Видео:2031 окружность центром в точке О описана около равнобедренного треугольника ABCСкачать

Укажите номера верных утверждений : 1) Центром описанной окружности треугольника является точка пересечения его высот 2)центром описанной окружности треугольника является точка пересечения его медиан ?

Укажите номера верных утверждений : 1) Центром описанной окружности треугольника является точка пересечения его высот 2)центром описанной окружности треугольника является точка пересечения его медиан 3)центром описанной окружности треугольника является точка пересечения его биссектрис.

Видео:Вписанная и описанная окружности | Лайфхак для запоминанияСкачать

Укажите номера верных утверждений?

Укажите номера верных утверждений.

1) В треугольнике против меньшего угла лежит большая сторона.

2) Центром окружности, описанной около правильного треугольника, является точка пересечения его биссектрис.

3) Каждая сторона треугольника больше сумы двух других сторон.

Видео:№706. Найдите сторону равностороннего треугольника, если радиус описанной около него окружностиСкачать

Верны ли утверждения : 1 центром окружности описанной околотреугольника , являестся точка пересечения его биссектрис?

Верны ли утверждения : 1 центром окружности описанной околотреугольника , являестся точка пересечения его биссектрис.

2 Центром окружности, описанной около прямоугольного треугольника, находится на стороне этого треугольника.

3 Если в четырехугольнике два угла — прямые, то этот четырёх уголь ни ей параллелограмм.

4 Квадрат любой стороны треугольника равен сумме квадратов двух других без произведения этих сторон на косинус угла между ними.

Видео:ОГЭ 2020 задание 17Скачать

Правильно ли?

Центром окружности, описанной около правильного треугольника, является точка пересечения его высот.

Видео:Разбор 16 и 23 задание ОГЭ по математике 2023 | УмскулСкачать

Какие из следующих утверждений верны?

1) Около всякого треугольника можно описать не более одной окружности.

2) В любой треугольник можно вписать не менее одной окружности.

3) Центром окружности, описанной около треугольника, является точка пересечения биссектрис.

4) Центром окружности, вписанной в треугольник, является точка пересечения серединных перпендикуляров к его сторонам.

На странице вопроса Укажите номера верных утверждений? из категории Геометрия вы найдете ответ для уровня учащихся 5 — 9 классов. Если полученный ответ не устраивает и нужно расшить круг поиска, используйте удобную поисковую систему сайта. Можно также ознакомиться с похожими вопросами и ответами других пользователей в этой же категории или создать новый вопрос. Возможно, вам будет полезной информация, оставленная пользователями в комментариях, где можно обсудить тему с помощью обратной связи.

Пусть в треугольнике ABC известны стороны AB = c, BC = b и медиана BM = m. На луче AM отложим отрезок MD, MD = AM и соединим точку D с точками B и C. Поскольку в полученном четырехугольнике ABCD диагонали точкой пересечения делятся пополам, то ABCD..

∠АВС = ∠А₁АС + ∠С₁СА ∠А₁АС = ∠С₁СА = х х + х + 130 = 180 2х + 130 = 180 2х = 180 — 130 2х = 50 х = 25 = ∠А₁АС = ∠С₁СА Тогда : ∠АВС = 25 + 25 = 50 Пусть ∠А = ∠С = у Тогда : у + у + 50 = 180 2у + 50 = 180 2у = 130 у = 65 = ∠А = ∠С ∠АА₁В = 180 — (ВАА₁ +..

Весь циферблат равен 360°. Каждые 5 минут — это 30° (360 : 12 = 30). 5 час — это отсек 25 минуты. Так же известно, что есть 10 минут. Получается, что угол занимает по три пятиминутки ((25 — 10) : 5 = 3) Узнаём градусную меру : 3•30° = 90°.

Большая дуга относится к меньшей как 4 : 1. Т. е. Большая дуга — 4 части, меньшая — 1 часть. Вся окружность — 5 частей. Градусная мера окружности 360°, откуда 1 часть = 360° : 5 = 72°. Это меньшая дуга. Большая дуга = 72 * 4 = 288°. Ответ : 72..

По теореме Пифагора : смНайдем синус угла B : sinB = AC / AB = 5 / 10 = 1 / 2значит, В = 30 градусов.

ABCD — трапеция (буквы можешь расположить, как хочешь)AC — диагональBC = 10L ACB = L DL CAD = L ACB (по свойству трапеции) — — — — — — > L D = L CAD — — — — — > AC = CDL ACB = L CAD — — — — — > L BAD = 90 град. — — — — > L D = L CAD = L ACB = 90 2..

M(x1 ; y1) n(x2 ; y2) середина = ((x2 — x1) / 2 ; (y2 — y1) / 2) 1) (5 ; 2) 2)(1 ; 3) 3)(1, 5 ; 4, 5).

S = 6 * 10 * 8 * 20 = 9600 Вот.

Всё 12 ребер у куба равны. Найдем длину одного : 48 : 12 = 4 Все 6 граней — равные квадраты. Тогда площадь S = 6 * 4² = 6 * 16 = 96.