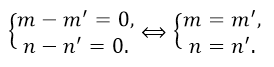Чему равны координаты векторов mn kl op (7 видео)

Онлайн калькулятор. Координаты вектора по двум точкам.

Этот онлайн калькулятор позволит вам очень просто найти значение координат вектора по двум точкам (зная его начальную и конечную точку) для плоских и пространственных задач.

Воспользовавшись онлайн калькулятором, вы получите детальное решение вашей задачи, которое позволит понять алгоритм решения задач на определение координат вектора по двум точкам и закрепить пройденый материал.

Содержание

Калькулятор для вычисления координат вектора по двум точкам
Инструкция использования калькулятора для вычисления координат вектора по двум точкам
Ввод даных в калькулятор для вычисления координат вектора по двум точкам
Дополнительные возможности калькулятора для вычисления координат вектора по двум точкам
Теория. Координаты вектора по двум точкам
Как найти координаты вектора
Предварительные сведения
Готовые работы на аналогичную тему
Координаты вектора
Линейные операции над векторами
Пример задачи на нахождение координат вектора
Декартовы координаты и векторы в пространстве
Координаты вектора
Линейные операции над векторами
🎥 Видео

Видео:9 класс, 2 урок, Координаты вектораСкачать

Калькулятор для вычисления координат вектора по двум точкам

Инструкция использования калькулятора для вычисления координат вектора по двум точкам

Ввод даных в калькулятор для вычисления координат вектора по двум точкам

В онлайн калькулятор можно вводить числа или дроби. Более подробно читайте в правилах ввода чисел.

Дополнительные возможности калькулятора для вычисления координат вектора по двум точкам

Между полями для ввода можно перемещаться нажимая клавиши «влево» и «вправо» на клавиатуре.

Видео:Координаты вектора. 9 класс.Скачать

Теория. Координаты вектора по двум точкам

Например, вектор AB , заданный в пространстве координатами точек A(A _x , A _y , A _z ) и B(B _x , B _y , B _z ) можно найти использовав формулу:

Вводить можно числа или дроби (-2.4, 5/7, . ). Более подробно читайте в правилах ввода чисел.

Видео:Координаты вектора в пространстве. 11 класс.Скачать

Как найти координаты вектора

Вы будете перенаправлены на Автор24

Видео:Скалярное произведение векторов через координаты. 9 класс.Скачать

Предварительные сведения

Здесь мы ограничимся двумерным случаем. Введение понятия для трехмерного случая проводится аналогично. Для того, чтобы ввести понятие координат вектора сначала введем и докажем следующие лемму и теорему.

Доказательство.

Возможны два случая:

Из этого всего следует, что $overrightarrow=koverrightarrow$.

Из этого всего следует, что $overrightarrow=koverrightarrow$.

Лемма доказана.

Любой вектор можно разложить по двум неколлинеарным векторам, причем коэффициенты разложения определяются единственным образом:

Доказательство.

Существование: Докажем, что такое разложение имеет место. Здесь возможны два случая:

Вектор $overrightarrow$ коллинеарен (к примеру) вектору $overrightarrow$.

По лемме 1, будем иметь

Значит, если число $m=0$, то получим

Вектор $overrightarrow$ не коллинеарен векторам $overrightarrow$ и $overrightarrow$.

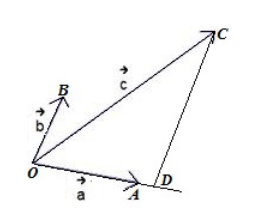
Возьмем произвольную точку $O$ и отложим от нее векторы $overrightarrow=overrightarrow, overrightarrow=overrightarrow$ и $overrightarrow=overrightarrow$. Пусть Проведем прямую $CD||OB$ (рис. 1)

Рисунок 1. Иллюстрация теоремы 1

По правилу треугольника для сложения векторов, получим

Готовые работы на аналогичную тему

Следовательно, разложение единственно.

Теорема доказана.

Видео:Векторы. Метод координат. Вебинар | МатематикаСкачать

Координаты вектора

Рассмотрим далее систему координат. От начала координат $O$ в направлении оси $Ox$ отложим вектор $overrightarrow$, а в направлении оси $Oy$ отложим вектор $overrightarrow$, длины которых равны единице.

Векторы $overrightarrow$ и $overrightarrow$ называются координатными векторами.

Так как векторы $overrightarrow$ и $overrightarrow$ не коллинеарны то, по теореме 1, любой вектор можно разложить в виде $overrightarrow=moverrightarrow+noverrightarrow$.

Коэффициенты разложения вектора $overrightarrow=moverrightarrow+noverrightarrow$ называются координатами данного вектора в данной системе координат, то есть

Видео:Нахождение координат вектора. Практическая часть. 9 класс.Скачать

Линейные операции над векторами

Теорема о сумме векторов: Координаты суммы векторов равны сумме соответствующих координат этих векторов.

Доказательство.

Докажем теорему для двух векторов. Теорема для большего количества векторов доказывается аналогично. Пусть $overrightarrow=left$, $overrightarrow=$, тогда

Теорема доказана.

Теорема о разности векторов: Координаты разности векторов равны разности соответствующих координат этих векторов.

Доказательство.

Теорема доказана.

Теорема о произведении вектора на число: Координаты произведения вектора на число равны произведению соответствующих координат это число.

Доказательство.

Теорема доказана.

Видео:Координаты точки и координаты вектора 1.Скачать

Пример задачи на нахождение координат вектора

Решение.

Получи деньги за свои студенческие работы

Курсовые, рефераты или другие работы

Автор этой статьи Дата последнего обновления статьи: 05 04 2022

Видео:Нахождение длины вектора через координаты. Практическая часть. 9 класс.Скачать

Декартовы координаты и векторы в пространстве

Декартовы координаты — система координат, состоящая из двух перпендикулярных осей. Положение точки в такой системе формируется с помощью двух чисел, определяющих расстояние от центра координат по каждой из осей.

Здесь мы будем рассматривать трехмерный случай. Введем, для начала, следующие данные.

Рассмотрим два следующих случая:

Из этого всего следует, что ( overrightarrow=koverrightarrow ) .

Теорема 1 Произвольный вектор ( overrightarrow

) можно разложить по трем некомпланарным векторам ( overrightarrow, overrightarrow ) и ( overrightarrow ) с единственными коэффициентами разложения.

Математически это можно записать следующим образом

Существование: Пусть нам даны три некомпланарных вектора ( overrightarrow , overrightarrow ) и ( overrightarrow ) . Выберем произвольную точку ( O ) и построим следующие векторы:

( overrightarrow =overrightarrow, overrightarrow =overrightarrow, overrightarrow =overrightarrow и overrightarrow

=overrightarrow )

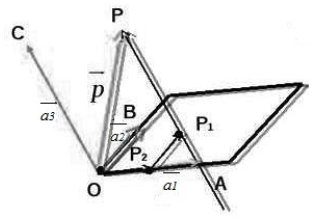
Рассмотрим следующий рисунок:

Рисунок 1.

Произведем следующие дополнительные построения. Проведем через точку ( P ) прямую, которая будет параллельна вектору ( overrightarrow ) . Пусть эта прямая пересекает плоскость ( OAB ) в точке ( P_1 ) . Далее, проведем через точку ( P_1 ) прямую, которая будет параллельна вектору ( overrightarrow ) . Пусть эта прямая пересекает прямую ( OA ) в точке ( P_2 ) (смотри рисунок выше).

Воспользуемся свойством правила треугольника сложения двух векторов ( overrightarrow+overrightarrow=overrightarrow ) , получим:

Так как векторы ( overrightarrow ) и ( overrightarrow ) коллинеарны, то ( overrightarrow=_1overrightarrow=_1overrightarrow )

Так как векторы ( overrightarrow

) и ( overrightarrow ) коллинеарны, то ( overrightarrow

=_2overrightarrow=_2overrightarrow )

Так как векторы ( overrightarrow

) и ( overrightarrow ) коллинеарны, то ( overrightarrow

=_3overrightarrow=_3overrightarrow )

Тогда, получаем, что ( overrightarrow

=overrightarrow+overrightarrow

+overrightarrow

=_1overrightarrow +_2overrightarrow +_3overrightarrow )

Существование разложения доказано.

Единственность: Предположим противное. Пусть существует еще одно разложение вектора ( overrightarrow

) по векторам ( overrightarrow , overrightarrow ) и ( overrightarrow ) :

Вычтем эти разложения друг из друга

Из этого получаем

Доказано.

Видео:90. Координаты вектора Скачать

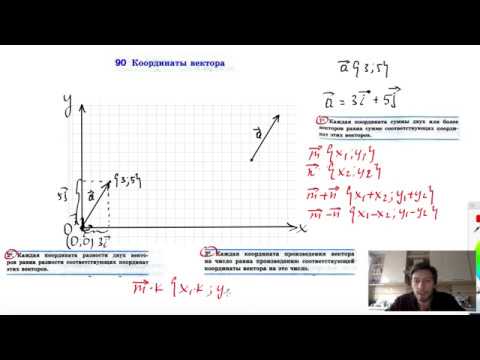
Координаты вектора

Рассмотрим декартову систему координат, которая строится следующим образом. Обозначим начало координат точкой ( O ) , по направлению оси ( Ox ) построим вектор ( overrightarrow ) , по направлению оси ( Oy ) построим вектор ( overrightarrow ) , а в направлении оси ( Oz ) отложим вектор ( overrightarrow ) , длины которых равны единице.

Определение 1 Векторы ( overrightarrow ) , ( overrightarrow ) , ( overrightarrow ) координатные векторы.

Из того что векторы ( overrightarrow ) , ( overrightarrow ) и ( overrightarrow ) не коллинеарны, по теореме 1, следует, что любой вектор можно разложить в виде ( overrightarrow=_1overrightarrow+_2overrightarrow+_3overrightarrow ) .

Определение 2 Коэффициенты в разложении вектора ( overrightarrow=_1overrightarrow+_2overrightarrow+_3overrightarrow ) называют координатами вектора в данной системе координат, то есть ( overrightarrow=<_1, _2,_3> )

Видео:Геометрия 9 класс (Урок№8 - Связь между координатами вектора и координатами его начала и конца.)Скачать

Линейные операции над векторами

Теорема 2 Координаты суммы векторов равны сумме соответствующих координат этих векторов.

Докажем теорему для двух векторов. Теорема для большего количества векторов доказывается аналогично. Пусть ( overrightarrow=left ) , ( overrightarrow= ) , тогда

Теорема доказана.

Теорема 3 Координаты разности векторов равны разности соответствующих координат этих векторов.

Теорема доказана.

Теорема 4 Координаты произведения вектора на число равны произведению соответствующих координат это число.

Теорема доказана.