Чему равен поток вектора е через поверхность полусферы s (5 видео)

Теорема Гаусса

Время чтения: 10 минут

До того, как мы рассмотрим теорему Гаусса, поговорим о том, кто же ее открыл и применил на практике.

Карл Фридрих Гаусс 1777-1855 г. Немецкий математик — один из великих, который не уступает Ньютону и Архимеду. Родился в Брауншвейге, в крестьянской семье.

Гениальная способность к математике проявилась уже в детстве и, пораженный чудесным талантом, учитель начальных классов убеждал родителей Карла не отдавать мальчика в ремесленную школу, а предоставить возможность продолжить образование. В четырнадцать лет Гаусс буквально удивился своим обширным знанием графа Брауншвейгского, и он дал юноше стипендию.

Большую часть своих важных математических исследований Гаусс сделал до того, как в 1799 г. он получил ученую степень доктора наук в Гёттингенском университете, а через два года выпустил свой фундаментальный труд «Трактат о математике», посвященный его влиятельному покровителю.

В трактате речь шла об арифметике — разделе математики, который занимается, прежде всего, натуральными числами и отношениями между ним, например, такими как Великая теорема Ферма. Впоследствии Гаусс не оставил свои занятия математикой, формулируя ряд принципов теоретической вероятности и математики, в том числе распределения случайной величины вокруг средней величины, которое было названо распределением Гаусса.

В 1801 г., когда был открыт первый астероид Церера, Гаусс обратился к астрологии. Чтобы рассчитать параметры орбиты, он разработал методику наименьшего квадрата, которая позволяет полностью рассчитывать орбиту солнечного спутника по результатам только трех измерений положения его места на орбите около Солнца. Через пять лет ученый был назначен директором Гёттингенской обсерватория и остался на этом посту до конца своей жизни. К тому же Гаусс был первым, кто всерьёз занимался изучением земной магнетизма, и именно в честь него названа единица магнитной напряженности.

В науке нередко бывает так, что один и тот же закон может быть сформулирован по-разному. В большинстве случаев формулировка закона не меняет ничего в плане его действий, но новые формулировки помогают теоретикам чуть иначе трактовать его и проверять его в отношении новых природных явлений. Именно таким образом можно рассмотреть теорему Гаусса — это, по сути, обобщение закона Кулона, который, в своей очередь, был обобщением всех знаний ученых об электростатических зарядах.

В математике, физике, астрономии найдется немного областей, развитию которых не посодействовал замечательный гений Карла Фридриха Гаусса.

В 1831 г. вместе с юным коллегой Вилгельмом Вебером (1804-1891 г.) он начал изучать электричество и магнетизм, вскоре сформулировав и доказав теорему, которая носит его имя. Для понимания её смысла представьте изолированный точечный электрический заряд Q. А сейчас представьте себе, что его окружает замкнутая поверхность. В теореме форма поверхности не важна – это может оказаться даже сдутым воздушным шариком.

В каждой точке окружающей заряд поверхности, наблюдается электрическое поле, образованное зарядом, а произведение напряженности этого электрического поля на сколь угодно малую единицу площади окружающей заряд поверхности, через которую проходят силовые линии поля, называется потоком напряженности электрического поля, и можно рассчитать поток напряженности, приходящийся на каждый элемент поверхности. В теореме Гаусса говорится, что общий поток электрической напряженности, проходящий по окружающей поверхности заряда, пропорционален величине зарядов.

Связь между законом Кулона и теоремой Гаусса можно рассмотреть на простом примере. Предположим, что заряд q окружен сферой радиуса r. На удалении r от заряда напряженность электрического поля, которая определяется силой притяжения или отталкивания единичного заряда, помещенного в соответствующую точку, составит, согласно закону Кулона:

И то же самое значение мы получим для любой точки сферы заданного радиуса. Следовательно, суммарный поток напряженности электрического поля будет равен значению напряженности поля на удалении r от заряда, помноженному на площадь сферы (которая, как известно, равняется 4πr2). Иными словами, суммарный поток будет равен:

Формула теоремы Гаусса

[4 pi r^ times k q / r^=4 pi k q]

Содержание

Применение формулы Гаусса
Теорема Гаусса
Поток вектора напряженности
Теорема Гаусса. Доказательство
Применение теоремы Гаусса
Вычислить поток вектора напряжённости электростатического поля через полусферу радиусом R = 2 см. Поле Е = 1000 В/м однородно и параллельно оси полусферы. Готовое решение: Заказ №8240
Описание и исходные данные задания, 50% решения + фотография:
🌟 Видео

Видео:Урок 222. Поток вектора напряженности электрического поляСкачать

Применение формулы Гаусса

Формула применяется для преобразования объемного интеграла в интеграл на замкнутую поверхность и обратно. В математическом анализе формула Теоремы Остроградского — Гаусса применяется для расчета дифференциации, т.е. потока вектора по поверхности окружающей среды внешними направлениями.

Принимая во внимание то, что поток векторного поля через замкнутую поверхность δδ в направлении внешней единичной нормали n0¯¯¯¯¯n0¯ равен дивергенции данного поля, вычисленной по телу TT, которое эта поверхность.

Видео:Билет №02 "Теорема Гаусса"Скачать

Теорема Гаусса

Для полноценного описания электростатического поля заданной системы зарядов в вакууме достаточно экспериментально подтвержденного закона Кулона и принципа суперпозиции. Но при этом существует возможность свойства электростатического поля охарактеризовать в ином обобщенном виде, не опираясь на утверждения касательно кулоновского поля точечного заряда.

Видео:Поток вектора напряженности электрического поля. Теорема Гаусса. 10 класс.Скачать

Поток вектора напряженности

Зададим новую физическую величину, описывающую электрическое поле – поток Φ вектора напряженности электрического поля. Предположим, что в пространстве, содержащем заданное электрическое поле, имеется некая достаточно малая площадка Δ S .

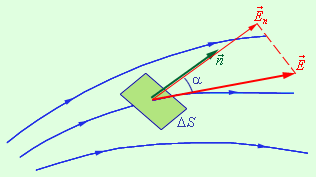
Элементарный поток вектора напряженности (через площадку S ) – это физическая величина, равная произведению модуля вектора E → , площади Δ S и косинуса угла α между вектором и нормалью к площадке:

Δ Φ = E Δ S cos α = E n Δ S.

В данной формуле E n является модулем нормальной составляющей поля E → .

Рисунок 1 . 3 . 1 . Иллюстрация элементарного потока Δ Φ .

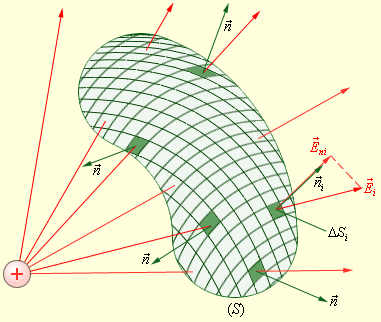
Теперь возьмем для рассмотрения некую произвольную замкнутую поверхность S . Разобьем заданную поверхность на площадки небольшого размера Δ S i , рассчитаем элементарные потоки Δ Φ i поля через эти малые площадки, после чего найдем их сумму, что в итоге даст нам поток Φ вектора через замкнутую поверхность S (рис. 1 . 3 . 2 ):

Φ = ∑ ∆ Φ i = ∑ E m ∆ S i

Когда речь идет о поверхности замкнутого типа, всегда используется внешняя нормаль.

Рисунок 1 . 3 . 2 . Расчет потока Ф через произвольную замкнутую поверхность S .

Видео:Урок 223. Теорема ГауссаСкачать

Теорема Гаусса. Доказательство

Теорема или закон Гаусса для электростатического поля в вакууме является одним из основных электродинамических законов.

Поток вектора напряженности электростатического поля E → через произвольную замкнутую поверхность равен алгебраической сумме зарядов, расположенных внутри этой поверхности, деленной на электрическую постоянную ε 0 .

Уравнение Гаусса имеет вид:

Φ = 1 ε 0 ∑ q в н у т р

Докажем указанную теорию: для этого исследуем сферическую поверхность (или поверхность шара) S . В центре заданной поверхности расположен точечный заряд q . Любая точка сферы обладает электрическим полем, перпендикулярным поверхности сферы и равным по модулю:

E = E n = 1 4 π ε 0 · q R 2 ,

где R является радиусом сферы.

Поток Φ через поверхность шара запишется, как произведение E и площади сферы 4 π R 2 . Тогда: Φ = 1 ε 0 q .

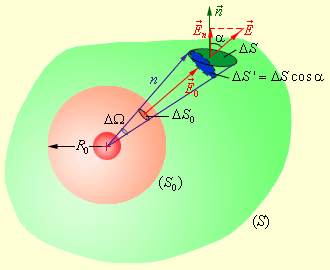
Следующим нашим шагом будет окружение точечного заряда произвольной поверхностью S замкнутого типа; зададим также вспомогательную сферу R 0 (рис. 1 . 3 . 3 ).

Рисунок 1 . 3 . 3 . Поток электрического поля точечного заряда через произвольную поверхность S , окружающую заряд.

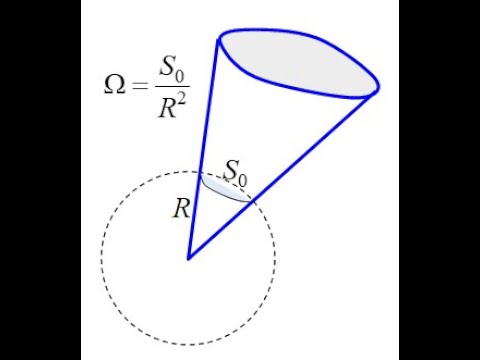
Возьмем для рассмотрения конус с малым телесным углом Δ Ω при вершине. Рассматриваемый конус задаст на сфере малую площадку Δ S 0 , а на поверхности S – площадку Δ S . Элементарные потоки Δ Φ 0 и Δ Φ через эти площадки являются одинаковыми. В самом деле:

Δ Φ 0 = E 0 Δ S 0 , Δ Φ = E Δ S cos α = E Δ S ‘ ,

где выражением Δ S ‘ = Δ S cos α определяется площадка, которая задастся конусом с телесным углом Δ Ω на поверхности сферы радиуса n .

Поскольку ∆ S 0 ∆ S ‘ = R 0 2 r 2 , то ∆ Φ 0 = ∆ Φ . Из полученного следует вывод о том, что полный поток электрического поля точечного заряда через произвольную поверхность, охватывающую заряд, равен потоку Φ 0 через поверхность вспомогательной сферы:

Так же мы можем продемонстрировать, что, когда замкнутая поверхность S не охватывает точечный заряд q , поток Φ равен нулю. Этот случай проиллюстрирован на рис. 1 . 3 . 2 . Все силовые линии электрического поля точечного заряда пронизывают замкнутую поверхность S насквозь. Внутри поверхности S зарядов нет, т.е. в этой области не наблюдается обрыва или зарождения силовых линий.

Обобщение теоремы Гаусса на случай произвольного распределения зарядов является следствием из принципа суперпозиции. Поле любого распределения зарядов возможно записать в виде векторной суммы электрических полей точечных зарядов. Поток Φ системы зарядов через произвольную замкнутую поверхность S сложится из потоков Φ i электрических полей отдельных зарядов. Когда заряд q i расположен внутри поверхности S , он дает вклад в поток, равный q i ε 0 . В случае расположения заряда снаружи поверхности его вклад в поток есть нуль.

Так, мы доказали теорему Гаусса.

Теорема Гаусса, по сути, есть следствие закона Кулона и принципа суперпозиции. Однако, взяв за изначальную аксиому утверждения теоремы, следствием станет закон Кулона, в связи с чем теорему Гаусса порой называют альтернативной формулировкой закона Кулона.

Опираясь на теорему Гаусса, в определенных случаях легко определить напряженность электрического поля вокруг заряженного тела (при наличии заранее угаданных симметрии заданного распределения зарядов и общей структуры поля).

Видео:Применение теоремы Гаусса-Остроградского. Напряжённость поля пластины, сферы и шара.Скачать

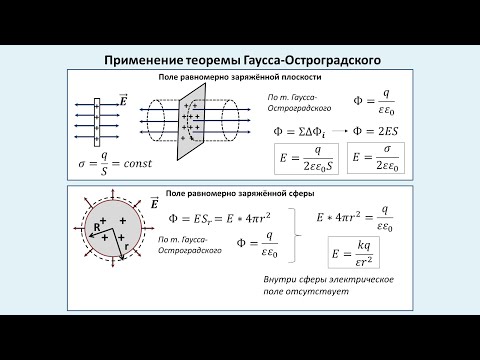
Применение теоремы Гаусса

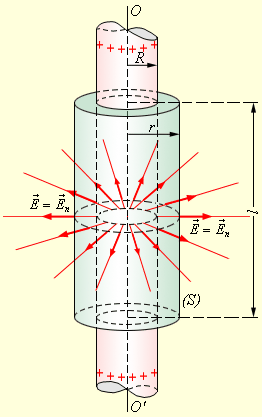
В качестве примера можно рассмотреть задачу, в которой необходимо вычислить поле тонкостенного полого однородно заряженного длинного цилиндра с радиусом R . Такая задача имеет осевую симметрию, и из соображений симметрии электрическое поле должно иметь направление по радиусу. Таким образом, чтобы иметь возможность применить теорему Гаусса, оптимально выбрать поверхность замкнутого типа S в виде соосного цилиндра некоторого радиуса r и длины l , закрытого с обоих торцов (рис. 1 . 3 . 4 ).

Рисунок 1 . 3 . 4 . Иллюстрация поля однородно заряженного цилиндра. O O ‘ – ось симметрии.

Если r ≥ R , то весь поток вектора напряженности пройдет через боковую поверхность цилиндра, поскольку поток через оба основания есть нуль. Формула площади боковой поверхности цилиндра запишется как: 2 π r l . Применим закон Гаусса и получим:

Φ = E 2 π r l = τ l ε 0 .

В указанном выражении τ является зарядом длины цилиндра. Далее можно записать:

Данное выражение не имеет зависимости от радиуса R заряженного цилиндра, а значит оно применимо и к полю длинной однородно заряженной нити.

Чтобы найти напряженность поля внутри заряженного цилиндра, необходимо создать замкнутую поверхность для случая r R . В соответствии с симметрией задачи поток вектора напряженности через боковую поверхность цилиндра должен быть, и в этом случае он равен Φ = E 2 π r l . Исходя из гауссовской теоремы, этот поток находится в пропорции к заряду, расположенному внутри замкнутой поверхности. Заряд этот равен нулю, откуда вытекает, что электрическое поле внутри однородно заряженного длинного полого цилиндра тоже есть нуль.

Точно так же теорема и формула Гаусса применимы для определения электрического поля в иных случаях, когда распределение зарядов охарактеризовано какой-либо симметрией, к примеру, симметрией относительно центра, плоскости или оси. Во всех этих случаях необходимо выбирать замкнутую гауссову поверхность подходящей формы.

К примеру, в случае центральной симметрии поверхность оптимально выбрать в виде сферы, у которой центр расположен в точке симметрии. Когда мы имеем симметрию относительно оси, подходящим видом замкнутой поверхности будет соосный цилиндр, закрытый с обоих торцов (аналогично рассмотренному выше примеру).

При отсутствии симметрии и невозможности угадать общую структуру поля, теорема Гаусса не сможет быть применена для упрощения решения задачи по определению напряженности поля.

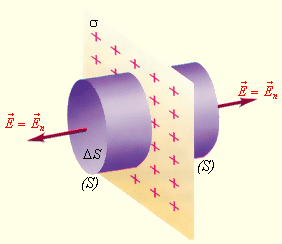
Разберем еще пример распределения зарядов при наличии симметрии: нахождение поля равномерно заряженной плоскости (рис. 1 . 3 . 5 ).

Рисунок 1 . 3 . 5 . Поле равномерно заряженной плоскости. σ – поверхностная плотность заряда. S – замкнутая гауссова поверхность.

Здесь гауссову поверхность S оптимально задать как цилиндр некой длины, замкнутый с обоих концов. Ось цилиндра является перпендикуляром к заряженной плоскости; в свою очередь, торцы цилиндра находятся на одинаковом расстоянии от нее. В соответствии с симметрией поле равномерно заряженной плоскости должно везде иметь направление по нормали. Применим теорему Гаусса и получим:

2 E ∆ S = σ ∆ S ε 0 или E = σ 2 ε 0 .

Здесь σ является поверхностной плотностью заряда или зарядом, приходящимся на единицу площади.

Выражение, которое мы получили для электрического поля однородно заряженной плоскости, возможно использовать и для плоских заряженных площадок конечного размера: здесь расстояние от точки, в которой мы определяем напряженность поля, до заряженной площадки должно быть значимо меньше размеров площадки.

Видео:Физика. 10 класс. Поток вектора напряженности электрического поля. Теорема Гаусса /18.01.2021/Скачать

Вычислить поток вектора напряжённости электростатического поля через полусферу радиусом R = 2 см. Поле Е = 1000 В/м однородно и параллельно оси полусферы. Готовое решение: Заказ №8240

Готовое решение: Заказ №8240

Тип работы: Задача

Статус: Выполнен (Зачтена преподавателем ВУЗа)

Предмет: Физика

Дата выполнения: 12.08.2020

Цена: 118 руб.

Чтобы получить решение , напишите мне в WhatsApp , оплатите, и я Вам вышлю файлы.

Кстати, если эта работа не по вашей теме или не по вашим данным , не расстраивайтесь, напишите мне в WhatsApp и закажите у меня новую работу , я смогу выполнить её в срок 1-3 дня!

Описание и исходные данные задания, 50% решения + фотография:

Вычислить поток вектора напряжённости электростатического поля через полусферу радиусом R = 2 см. Поле Е = 1000 В/м однородно и параллельно оси полусферы.

Дано: R = 2 см=0,02 м Е = 1000 В/м

Поток вектора равен где — угол между векторами и Направим ось z вдоль поля. Найдем поток напряженности через поверхность полусферы. Используя сферические координаты — углы и — для определения положения точки на полусфере, мы видим, что и Поэтому поток через элементарную площадку на полусфере равен Учитывая, что а записываем поток в виде откуда находим полный поток через поверхность полусферы.

Я и моя команда оказывает помощь в учёбе по любым предметам и заданиям любой сложности.

Решение задач является неотъемлемой частью обучения в любом учебном заведении, и я смогу помочь в решение задач по любым предметам.

Присылайте задания в любое время дня и ночи в ➔

Официальный сайт Брильёновой Натальи Валерьевны преподавателя кафедры информатики и электроники Екатеринбургского государственного института.

Все авторские права на размещённые материалы сохранены за правообладателями этих материалов. Любое коммерческое и/или иное использование кроме предварительного ознакомления материалов сайта natalibrilenova.ru запрещено. Публикация и распространение размещённых материалов не преследует за собой коммерческой и/или любой другой выгоды.

Сайт предназначен для облегчения образовательного путешествия студентам очникам и заочникам по вопросам обучения . Наталья Брильёнова не предлагает и не оказывает товары и услуги.