Сумма квадратов сторон треугольника

О чем эта статья:

Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).

Видео:Геометрия доказательство теоремы косинусов Квадрат стороны треугольника равен сумме квадратов двухСкачать

Основные понятия

Теорема Пифагора, определение: в прямоугольном треугольнике квадрат длины гипотенузы равен сумме квадратов длин катетов.

Гипотенуза — сторона, лежащая напротив прямого угла.

Катет — одна из двух сторон, образующих прямой угол.

Формула Теоремы Пифагора выглядит так:

где a, b — катеты, с — гипотенуза.

Из этой формулы можно вывести следующее:

• a = √c 2 − b 2
• b = √c 2 − a 2
• c = √a 2 + b 2

Для треугольника со сторонами a, b и c, где c — большая сторона, действуют следующие правила:

• если c 2 2 + b 2 , значит угол, противолежащий стороне c, является острым.
• если c 2 = a 2 + b 2 , значит угол, противолежащий стороне c, является прямым.
• если c 2 > a 2 +b 2 , значит угол, противолежащий стороне c, является тупым.

Видео:Теорема Пифагора для чайников)))Скачать

Теорема Пифагора: доказательство

В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.

Дано: ∆ABC, в котором ∠C = 90º.

Доказать: a 2 + b 2 = c 2 .

Пошаговое доказательство:

• Проведём высоту из вершины C на гипотенузу AB, основание обозначим буквой H.
• Прямоугольная фигура ∆ACH подобна ∆ABC по двум углам:

• Также прямоугольная фигура ∆CBH подобна ∆ABC:

• Введем новые обозначения: BC = a, AC = b, AB = c.

• Из подобия треугольников получим: a : c = HB : a, b : c = AH : b.

• Значит a 2 = c * HB, b 2 = c * AH.
• Сложим полученные равенства:

a 2 + b 2 = c * HB + c * AH

a 2 + b 2 = c * (HB + AH)

a 2 + b 2 = c * AB

Видео:Сумма квадратов диагоналей параллелограммаСкачать

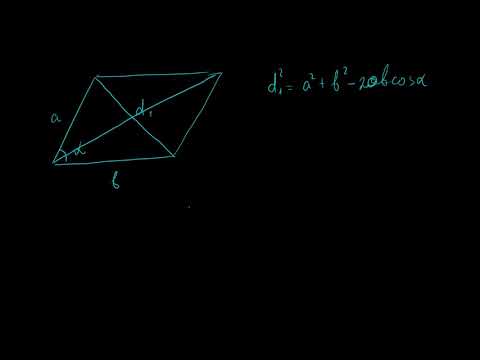
Обратная теорема Пифагора: доказательство

Если сумма квадратов двух сторон треугольника равна квадрату третьей стороны, то такой треугольник является прямоугольным.

Дано: ∆ABC

Доказать: ∠C = 90º

Пошаговое доказательство:

• Построим прямой угол с вершиной в точке C₁.
• Отложим на его сторонах отрезки C₁A₁ = CA и C₁B₁ = CB.

• Проведём отрезок A₁B₁.
• Получилась фигура ∆A₁B₁C₁, в которой ∠C₁=90º.

• В этой фигуре ∆A₁B₁C₁ применим теорему Пифагора: A₁B₁ 2 = A₁C₁ 2 + B₁C₁ 2 .
• Таким образом получится:

• Значит, в фигурах треугольниках ∆ABC и ∆A₁B₁C₁:

1. C₁A₁ = CA и C₁B₁ = CB по результату построения,
2. A₁B₁ = AB по доказанному результату.

• Поэтому, ∆A₁B₁C₁ = ∆ABC по трем сторонам.
• Из равенства фигур следует равенство их углов: ∠C =∠C₁ = 90º.

Обратная теорема доказана.

Видео:Нахождение стороны прямоугольного треугольникаСкачать

Решение задач

Задание 1. Дан прямоугольный треугольник ABC. Его катеты равны 6 см и 8 см. Какое значение у гипотенузы?

Как решаем:

Пусть катеты a = 6 и b = 8.

По теореме Пифагора c 2 = a 2 + b 2 .

Подставим значения a и b в формулу:
c 2 = 6 2 + 8 2 = 36 + 64 = 100
c = √100 = 10.

Задание 2. Является ли треугольник со сторонами 8 см, 9 см и 11 см прямоугольным?

• Выберем наибольшую сторону и проверим, выполняется ли теорема Пифагора:

Ответ: треугольник не является прямоугольным.

Видео:ТЕОРЕМА СИНУСОВ И ТЕОРЕМА КОСИНУСОВ. Тригонометрия | МатематикаСкачать

Треугольник. Числовые зависимости между элементами треугольника (сторон, высот, медиан).

Теорема.

Если стороны прямоугольного треугольника измерены одной единицей, то квадрат числа, выражающего гипотенузу равен сумме квадратов чисел, выражающих катеты.

Эту теорему обыкновенно выражают сокращенно так:

Квадрат гипотенузы равен сумме квадратов катетов.

Это соотношение было впервые замечено греческим геометром Пифагором (VI в. до н.э.) и носит поэтому его имя — теорема Пифагора.

В треугольнике квадрат стороны, лежащей против острого угла, равен сумме квадратов двух других сторон без удвоенного произведения какой-нибудь из этих сторон на ее отрезок от вершины острого угла до высоты.

Пусть BС — сторона треугольника ABС (черт. 1 и черт. 2), лежащая против острого угла A , и BD — высота опущенная на какую-либо из остальных сторон, например, на AС (или на ее продолжение).Требуется доказать, что:

Из прямоугольных треугольников BDС и ABD выводим:

Подставив в равенство [1] вместо BD 2 и DС 2 их выражения из равенств [2] и [3] , получим:

Это равенство, после сокращения членов -AD 2 и +AD 2 , и есть то самое, которое требовалось доказать.

Замечание. Доказанная теорема остается верной и тогда, когда угол С прямой. Тогда отрезок СD обратится в ноль, т.е. AС станет равна AD, и мы будем иметь:

Что согласуется с теоремой о квадрате гипотенузы.

Теорема.

В треугольнике квадрат стороны, лежащей против тупого угла, равен сумме квадратов двух других сторон, сложенных с удвоенным произведением какой-нибудь из этих сторон на отрезок ее продолжения от вершины тупого угла до высоты. Доказательство аналогично предыдущему.

Следствие.

Из трех последних теорем выводим, что квадрат стороны треугольника равен, меньше или больше суммы квадратов других сторон, смотря по тому, будет ли противолежащий угол прямой, острый или тупой.

Отсюда следует обратное предложение: Угол треугольника окажется прямым, острым или тупым, смотря по тому, будет ли квадрат противолежащей стороны равен, меньше или больше суммы квадратов других сторон.

Видео:Теорема ПИФАГОРА ❤️Скачать

Вычисление высоты треугольника по его сторонам.

Обозначим высоту, опущенную на сторону а треугольника ABС , через h_a. Чтобы вычислить ее, предварительно из уравнения:

находим отрезок основания с’:

.

После чего из DABD определяем высоту, как катет:

.

Таким же путем можно определить высоты h_b и h_с , опущенные на стороны b и с.

Видео:Теорема Пифагора в деле🦾 Длины сторон считаем по клеткам ☝️Скачать

Вычисление медиан треугольника по его сторонам.

Пусть даны стороны треугольника ABС и требуется вычислить его медиану BD. Для этого продолжим ее на расстояние DE = BD и точку E соединим с A и С. Тогда получим параллелограмм ABCE.

Тогда .

Видео:Площадь треугольника. Как найти площадь треугольника?Скачать

Теорема косинусов

Видео:8 класс, 16 урок, Теорема ПифагораСкачать

Формулировка теоремы косинусов

Для плоского треугольника со сторонами a,b,c и углом α, противолежащим стороне a, справедливо соотношение:

Полезные формулы теоремы косинусов:

Как видно из указанного выше, с помощью теоремы косинусов можно найти не только сторону треугольника по двум сторонам и углу между ними, можно, зная размеры всех сторон треугольника, определить косинусы всех углов, а также вычислить величину любого угла треугольника. Вычисление любого угла треугольника по его сторонам является следствием преобразования формулы теоремы косинусов.

Видео:Теорема Пифагора. 8 КЛАСС | Математика | TutorOnlineСкачать

Теорема Пифагора

Теорема Пифагора . В прямоугольном треугольнике сумма квадратов длин катетов равна квадрату длины гипотенузы .

Доказательство . Докажем, что длины сторон произвольного прямоугольного треугольника ABC (рис.1)

С этой целью рассмотрим квадрат квадрат со стороной, равной c , изображённый на рисунке 2.

Площадь этого квадрата равна сумме площадей четырёх одинаковых прямоугольных треугольников, равных треугольнику ABC (рис.3, рис.4), и площади квадрата со стороной, равной a – b (рис.5).

Рис.3

Рис.4

Рис.5

Поэтому справедливо равенство

что и требовалось доказать.

Видео:По силам каждому ★ Найдите стороны треугольника на рисункеСкачать

Формулировка теоремы косинусов для треугольника

Теорема косинусов для треугольника связывает две стороны треугольника и угол между ними со стороной, лежащей против этого угла. К примеру, обозначим буквами , , и длины сторон треугольника ABC, лежащие соответственно против углов A, B и C.

Тогда имеет теорема косинусов для этого треугольника может быть записана в виде:

На рисунке для удобства дальнейших рассуждений угол С обозначен углом . Словами это можно сформулировать следующим образом: «Квадрат любой стороны треугольника равен сумме квадратов двух других сторон за вычетом удвоенного произведения этих сторон на косинус угла между ними.»

Понятно, что если бы вы выражали другую сторону треугольника, например, сторону , то в формуле нужно было бы брать косинус угла A, то есть лежащего против искомой стороны в треугольнике, а справа в уравнении на своих местах стояли бы стороны , то в формуле нужно было бы брать косинус угла A, то есть лежащего против искомой стороны в треугольнике, а справа в уравнении на своих местах стояли бы стороны и . Выражение для квадрата стороны . Выражение для квадрата стороны получается аналогично:

Видео:№953. Докажите, что сумма квадратов всех сторон параллелограмма равна сумме квадратов его диагоналейСкачать

Классическое доказательство теоремы косинусов.

Пусть есть треугольник ABC. Из вершины C на сторону AB опустили высоту CD. Значит:

Записываем теорему Пифагора для 2-х прямоугольных треугольников ADC и BDC:

h 2 = b 2 – (b cos α) 2 (1)

h 2 = a 2 – (c – b cos α) 2 (2)

Приравниваем правые части уравнений (1) и (2):

b 2 – (b cos α) 2 = a 2 – (c – b cos α) 2

a 2 = b 2 + c 2 – 2bc cos α.

Если 1-н из углов при основании тупой (высота упирается в продолжение основания), полностью аналогичен рассмотренному выше.

Определить стороны b и c:

b 2 = a 2 + c 2 – 2ac cos β

c 2 = a 2 + b 2 – 2ab cos γ.

Видео:Как найти гипотенузу в прямоугольном треугольнике, минуя теорему Пифагора?Скачать

Формулировка и формула теоремы

В плоском треугольнике квадрат стороны равняется сумме квадратов двух других сторон минус удвоенное произведение данных сторон, умноженное на косинус угла между ними.

a 2 = b 2 + c 2 – 2bc cos α

Видео:Периметр треугольника. Как найти периметр треугольника?Скачать

Теорема косинусов для остроугольного треугольника.

Если угол острый, то справедлива формула:

a 2 = b 2 + c 2 −2bx

Видео:Сумма квадратов натуральных чиселСкачать

Доказательство теоремы косинусов для треугольника

Доказательство теоремы косинусов для треугольника проводят обычно следующим образом. Разбивают исходный треугольник на два прямоугольных треугольника высотой, а дальше играются со сторонами полученных треугольников и теоремой Пифагора. В результате после долгих нудных преобразований получаю нужный результат. Мне лично этот подход не по душе. И не только из-за громоздких вычислений, но ещё и потому что в этом случае приходится отдельно рассматривать случай, когда треугольник является тупоугольным. Слишком много трудностей.

Я предлагаю доказать эту теорему с помощью понятия «скалярного произведения векторов». Я сознательно иду на этот риск для себя, зная, что многие школьники предпочитают обходить эту тему стороной, считая, что она какая-то мутная и с ней лучше не иметь дела. Но нежелание возиться отдельно с тупоугольным треугольником во мне всё же пересиливает. Тем более, что доказательство в результате получается удивительно простым и запоминающимся. Сейчас вы в этом убедитесь.

Заменим стороны нашего треугольника следующими векторами:

Согласно правилам сложения векторов имеем: . Действительно, по правилу треугольника вектор, равный сумме двух векторов, отложенных последовательно один за другим, — это вектор с началом в начале первого вектора и концом в конце второго. Переносим . Действительно, по правилу треугольника вектор, равный сумме двух векторов, отложенных последовательно один за другим, — это вектор с началом в начале первого вектора и концом в конце второго. Переносим в правую часть равенства с противоположным знаком, в результате чего получаем следующее векторное выражение: .

Теперь возьмём скалярный квадрат обеих частей полученного выражения. В результате чего получим:

Я напоминаю, что по определению скалярное произведение векторов равно произведению длин этих векторов на косинус угла между ними. Из этого определения также следует, что скалярный квадрат вектора равен квадрату его длины. Действительно, ведь угол между вектором и им же самим равен нулю, то есть соответствующих косинус равен 1. То есть остаётся только квадрат длины вектора. Исходя из этого мы сразу получаем выражение для теоремы косинусов:

Что и требовалось доказать. Причём данное доказательство хорошо ещё тем, что позволяет лучше запомнить саму формулу. Ведь теперь становится понятным, откуда берётся этот хвост . Как раз из скалярного произведения. Ну и, как я уже говорил, это доказательство справедливо для любых треугольников: остроугольных, тупоугольных и прямоугольных. То есть угол . Как раз из скалярного произведения. Ну и, как я уже говорил, это доказательство справедливо для любых треугольников: остроугольных, тупоугольных и прямоугольных. То есть угол может быть острым, тупым или прямым. И не требуется рассматривать доказательство для каждого из этих случаев, что не может не радовать.

Кстати, в случае, когда угол прямой, мы получаем прямой, мы получаем , и выражение принимает следующий вид: . Что мы получили? Правильно! Это запись теоремы Пифагора. Квадрат гипотенузы равен сумме квадратов катетов. Так что ниточки постепенно сплетаются. То есть, как обычно говорят, теорема косинусов для треугольника есть обобщение теоремы Пифагора на случай произвольного треугольника, не обязательно прямоугольного.

Видео:ЗАДАЧА О СУММЕ КВАДРАТОВСкачать

Теорема косинусов

Теорема косинусов . Квадрат длины стороны треугольника равен сумме квадратов длин других сторон минус удвоенное произведение длин этих сторон на косинус угла между ними.

Доказательство . Рассмотрим сначала треугольник ABC , у которого углы A и С – острые (рис.6).

Докажем, что длины сторон этого треугольника удовлетворяют равенству

С этой целью проведём высоту BD из вершины B (рис.7).

В соответствии с определениями синуса и косинуса угла прямоугольного треугольника справедливы равенства

BD = c sin A, AD = c cos A, DC = b – AD = b – c cos A.

Из теоремы Пифагора , применённой к прямоугольному треугольнику BDC , получим

Таким образом, в случае треугольника ABC с острыми углами A и С теорема косинусов доказана.

Замечание 1 . Для того, чтобы получить полное доказательство теоремы косинусов, необходимо рассмотреть также и следующие случаи:

1. Угол A – острый, угол C – тупой (рис.8)

Угол A – прямой (рис. 9).

Угол A – тупой (рис.10).

Во всех перечисленных случаях доказательства теоремы косинусов проводятся совершенно аналогично тому, как это было сделано для случая острых углов A и C , и мы рекомендуем читателю провести эти доказательства в качестве полезного и несложного упражнения.

Замечание 2 . В случае, когда угол A является прямым углом, формула (1) принимает вид

откуда вытекает, что теорема Пифагора является частным случаем теоремы косинусов.

Замечание 3 . Если у треугольника известны длины всех сторон, то с помощью теоремы косинусов можно найти косинус любого угла треугольника, например,

Видео:Найдите площадь треугольника на рисунке ★ Два способа решенияСкачать

Примеры задач

Задание 1
В треугольнике известны длины двух сторон – 5 и 9 см, а также, угол между ними – 60°. Найдите длину третьей стороны.

Решение:
Применим формулу теоремы, приняв известные стороны за b и c, а неизвестную за a:
a 2 = 5 2 + 9 2 – 2 * 5 * 9 * cos 60° = 25 + 81 – 45 = 61 см 2 . Следовательно, сторона a = √ 61 см ≈ 7,81 см.

Задание 2
Самая большая сторона треугольника равна 26 см, а две другие – 16 и 18 см. Найдите угол между меньшими сторонами.

Решение:
Примем бОльшую сторону за a. Чтобы найти угол между сторонами b и c, воспользуемся следствием из теоремы:

Следовательно, угол α = arccos (-1/6) ≈ 99,59°.

Видео:9 класс, 15 урок, Решение треугольниковСкачать

Теорема косинусов для прямоугольного треугольника

Теорема косинусов для прямоугольного треугольника.

Рассмотрим прямоугольный треугольник ABC:

По теореме косинусов сторона «а» равна:

но угол А прямой, косинус прямого угла равен нулю, отсюда получаем:

Таким образом мы получили формулу теоремы Пифагора:

📽️ Видео

Сумма квадратов | Ботай со мной #061 | Борис Трушин |Скачать

№524. Стороны треугольника — 13 см, 5 см и 12 см. Найдите площадь этого треугольника.Скачать