 Вписанные четырехугольники и их свойства Вписанные четырехугольники и их свойства |
 Теорема Птолемея Теорема Птолемея |
Видео:Вписанные и описанные четырехугольники. Практическая часть. 9 класс.Скачать

Вписанные четырёхугольники и их свойства
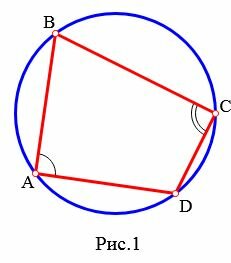
Определение 1 . Окружностью, описанной около четырёхугольника, называют окружность, проходящую через все вершины четырёхугольника (рис.1). В этом случае четырёхугольник называют четырёхугольником, вписанным в окружность, или вписанным четырёхугольником .
Теорема 1 . Если четырёхугольник вписан в окружность, то суммы величин его противоположных углов равны 180° .
Доказательство . Угол ABC является вписанным углом, опирающимся на дугу ADC (рис.1). Поэтому величина угла ABC равна половине угловой величины дуги ADC . Угол ADC является вписанным углом, опирающимся на дугу ABC . Поэтому величина угла ADC равна половине угловой величины дуги ABC . Отсюда вытекает, что сумма величин углов ABC и ADC равна половине угловой величины дуги, совпадающей со всей окружностью, т.е. равна 180° .
Если рассмотреть углы BCD и BAD , то рассуждение будет аналогичным.
Теорема 1 доказана.
Теорема 2 (Обратная к теореме 1) . Если у четырёхугольника суммы величин его противоположных углов равны 180°, то около этого четырёхугольника можно описать окружность.
Доказательство . Докажем теорему 2 методом «от противного». С этой целью рассмотрим окружность, проходящую через вершины A , B и С четырёхугольника, и предположим, что эта окружность не проходит через вершину D . Приведём это предположение к противоречию. Рассмотрим сначала случай, когда точка D лежит внутри круга (рис.2).
Продолжим отрезок CD за точку D до пересечения с окружностью в точке E , и соединим отрезком точку E с точкой A (рис.2). Поскольку четырёхугольник ABCE вписан в окружность, то в силу теоремы 1 сумма величин углов ABC и AEC равна 180° . При этом сумма величин углов ABC и ADC так же равна 180° по условию теоремы 2. Отсюда вытекает, что угол ADC равен углу AEC . Возникает противоречие, поскольку угол ADC является внешним углом треугольника ADE и, конечно же, его величина больше, чем величина угла AEC , не смежного с ним.
Случай, когда точка D оказывается лежащей вне круга, рассматривается аналогично.
Теорема 2 доказана.
Перечисленные в следующей таблице свойства вписанных четырёхугольников непосредственно вытекают из теорем 1 и 2.
| Фигура | Рисунок | Свойство | |||||||||||||||||||||||||||||||||||||||||
| Окружность, описанная около параллелограмма |  | Окружность можно описать около параллелограмма тогда и только тогда, когда параллелограмм является прямоугольником. | |||||||||||||||||||||||||||||||||||||||||
| Окружность, описанная около ромба |  | Окружность можно описать около ромба тогда и только тогда, когда ромб является квадратом. | |||||||||||||||||||||||||||||||||||||||||
| Окружность, описанная около трапеции |  | Окружность можно описать около трапеции тогда и только тогда, когда трапеция является равнобедренной трапецией. | |||||||||||||||||||||||||||||||||||||||||
| Окружность, описанная около дельтоида |  | Окружность можно описать около дельтоида тогда и только тогда, когда дельтоид состоит из двух одинаковых прямоугольных треугольников. | |||||||||||||||||||||||||||||||||||||||||
| Произвольный вписанный четырёхугольник |  | ||||||||||||||||||||||||||||||||||||||||||
| Окружность, описанная около параллелограмма | |||||||||||||
 | Окружность можно описать около параллелограмма тогда и только тогда, когда параллелограмм является прямоугольником. | ||||||||||||
| Окружность, описанная около ромба | |||||||||||||
 | Окружность можно описать около ромба тогда и только тогда, когда ромб является квадратом. | ||||||||||||
| Окружность, описанная около трапеции | |||||||||||||
 | Окружность можно описать около трапеции тогда и только тогда, когда трапеция является равнобедренной трапецией. | ||||||||||||
| Окружность, описанная около дельтоида | |||||||||||||
 | Окружность можно описать около дельтоида тогда и только тогда, когда дельтоид состоит из двух одинаковых прямоугольных треугольников. | ||||||||||||
| Произвольный вписанный четырёхугольник | |||||||||||||
 | |||||||||||||
| Окружность, описанная около параллелограмма |
 |
Окружность можно описать около параллелограмма тогда и только тогда, когда параллелограмм является прямоугольником.

Окружность можно описать около ромба тогда и только тогда, когда ромб является квадратом.

Окружность можно описать около трапеции тогда и только тогда, когда трапеция является равнобедренной трапецией.

Окружность можно описать около дельтоида тогда и только тогда, когда дельтоид состоит из двух одинаковых прямоугольных треугольников.

Площадь произвольного вписанного четырёхугольника можно найти по формуле Брахмагупты:
где a, b, c, d – длины сторон четырёхугольника,
а p – полупериметр, т.е.
Видео:3 правила для вписанного четырехугольника #shortsСкачать

Теорема Птолемея
Теорема Птолемея . Произведение диагоналей вписанного четырёхугольника равно сумме произведений противоположных сторон.
Доказательство . Рассмотрим произвольный четырёхугольник ABCD , вписанный в окружность (рис.3).
Докажем, что справедливо равенство:
Для этого выберем на диагонали AC точку E так, чтобы угол ABD был равен углу CBE (рис. 4).
Заметим, что треугольник ABD подобен треугольнику BCE . Действительно, у этих треугольников по два равных угла: угол ABD равен углу CBE (по построению точки E ), угол ADB равен углу ACB (эти углы являются вписанными углами, опирающимися на одну и ту же дугу). Следовательно, справедлива пропорция:
откуда вытекает равенство:
 | (1) |
Заметим, что треугольник ABE подобен треугольнику BCD . Действительно, у этих треугольников по два равных угла: угол ABE равен углу DBC (углы ABD и EBC равны по построению, угол DBE – общий), угол BAC равен углу BDC (эти углы являются вписанными углами, пирающимися на одну и ту же дугу). Следовательно, справедлива пропорция:
Видео:Четырехугольники, вписанные в окружность. 9 класс.Скачать

Биссектрисы углов четырехугольника вписанного в окружность
В четырехугольнике ABCD,вписанном в окружность, биссектрисы углов A и B пересекаются в точке E, лежащей на стороне CD. Известно, что CD : BC = 3 : 2.
а) Доказать, что расстояния от точки E до прямых AD и BC равны.
б) Найти отношение площадей треугольников ADE и BCE.
а) Расстояние от точки до прямой есть перпендикуляр, опущенный из данной точки на прямую.
Точки, лежащие на биссектрисе, равноудалены от сторон угла. Тогда точки, лежащие на биссектрисе AE угла A, равноудалены от сторон AD и AB, поэтому перпендикуляры EM и EN, соответственно проведенные к сторонам угла A, равны. Аналогично для угла B: все точки биссектрисы BE равноудалены от сторон BA и BC, поэтому перпендикуляры EN и EK равны. Отсюда получаем, что EM = EK. Что и требовалось доказать.
б) Обозначим ME = EK = r и выразим площади треугольников:
Выразим через углы и
стороны AD, BC и DC, предварительно найдя углы в данном четырехугольнике:
Из треугольников AME и BEK соответственно получаем:
Из треугольника MDE:
Из треугольника CKE:
Преобразуем полученные выражения для сторон:
Воспользуемся в числителе и знаменателе следующей формулой: откуда получим:
Осталось воспользоваться тем, что DC : BC = 3 : 2:
Обозначим для сокращения записи: Тогда:
Подставим z в искомую дробь и получим:
В итоге получили:
| Критерии оценивания выполнения задания | Баллы | |||
|---|---|---|---|---|
| Имеется верное доказательство утверждения пункта а и обоснованно получен верный ответ в пункте б. | 3 | |||
| Получен обоснованный ответ в пункте б. Имеется верное доказательство утверждения пункта а и при обоснованном решении пункта б получен неверный ответ из-за арифметической ошибки. | 2 | |||
| Имеется верное доказательство утверждения пункта а. При обоснованном решении пункта б получен неверный ответ из-за арифметической ошибки. Видео:Всё про углы в окружности. Геометрия | МатематикаСкачать  Четырехугольник, вписанный в окружностьОпределение 1. Четырехугольник называют вписанным в окружность, если все вершины четырехугольника лежат на окружности. На рисунке 1 четырехугольник ABCD вписан в окружность. В этом случае говорят также, что окружность описан около четырехугольника.
Теорема 1. Если четырехугольник вписан в окружность, то сумма противолежащих углов четырехугольника равна 180°. Доказательство. Пусть четырехугольник ABCD вписан в окружность (Рис.1). Докажем, что Углы A и C являются вписанными. Следовательно:
Но
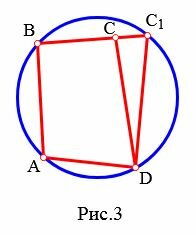
Аналогично можно показать, что Заметим, что из Как известно, вокруг любого треугольника можно описать окружность (см. статью Окружность, описанная около треугольника). Однако вокруг не каждого четырехугольника можно описать окружность. Например, если параллелограмм не является прямоугольником, то вокруг него не возможно описать окружность. Следующая теорема позволяет распознать четрехугольники, вокруг которых можно описать окружность. Теорема 2. Если в четырехугольнике сумма противолежащих углов равна 180°, то около него можно описать окружность. Доказательство. Пусть задан четырехугольник ABCD и пусть Предположим, что около этого четырехугольника невозможно описать окружность. Рассмотрим треугольник ABD и опишем окружность около этого треугольника (как отметили выше около любого треугольника можно описать окружность). Поскольку мы предположили, что у этого четырехугольника невозможно описать окружность, то точка C не принадлежит этой окружности. Поэтому эта точка лежит вне окружности или находится внутри окружности.
Случай 1. Точка C лежит вне описанной окружности (Рис.2). Тогда сторона BC пересекает этот окружность. Обозначим эту точку C1. Четырехугольник ABC1D вписан в окружность. Тогда по теореме 1 имеем: Случай 2. Точка C лежит внутри описанной окружности (Рис.3). Проведем прямую BC и точку пересечения прямой и окружности обозначим C1. Получили четырехугольник ABC1D вписанный в окружность. Тогда по теореме 1 имеем: С другой стороны, угол C (т.е. угол BCD) является внешним углом треугольника DC1C, т.е. выполняется равенство Следовательно точка C лежит на окружности. Теорема 2 можно рассматривать метод определения принадлежности четырех точек одной окружности. Если четырехугольник вписан в окружность, то существует точка, равноудаленная от всех вершин четырехугольника (это центр окружности). Чтобы найти эту точку достаточно построить серединные перпендикуляры двух соседних сторон четырехугольника и найти точку их пересечения. 💥 ВидеоЗадача повышенной трудности - Атанасян #891Скачать 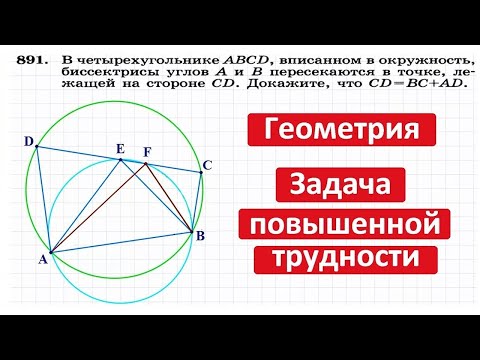 Вписанный в окружность четырёхугольник.Скачать  Геометрия Найдите углы четырехугольника MNKP, вписанного в окружность, если угол MKP = 58, угол MPNСкачать  Вписанная и описанная окружность - от bezbotvyСкачать  Вписанные четырехугольники. 9 класс.Скачать  ЗАДАНИЕ 1| ЕГЭ ПРОФИЛЬ| Угол А четырёхугольника ABCD, вписанного в окружность, равен 25.Найдите уголСкачать  Окружность вписанная в треугольник и описанная около треугольника.Скачать  8 класс, 35 урок, Свойства биссектрисы углаСкачать  Описанная и вписанная окружности четырехугольника - 8 класс геометрияСкачать  8 класс Геометрия. Окружность вписанная в четырехугольник и описанная около четырехугольника Урок #4Скачать  2041 четырёхугольник ABCD вписан в окружность угол abd равен 38 угол cаd равен 54 Найдите угол ABCСкачать  Четырёхугольник ABCD вписан в окружность ... | ОГЭ 2017 | ЗАДАНИЕ 10 | ШКОЛА ПИФАГОРАСкачать  Построение биссектрисы угла. 7 класс.Скачать  11 класс, 43 урок, Вписанный четырехугольникСкачать  3 свойства биссектрисы #shortsСкачать  ПОСТРОЕНИЕ БИССЕКТРИСЫ 😉 #егэ #математика #профильныйегэ #shorts #огэСкачать  |









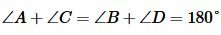 .
.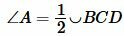 ,
, 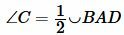
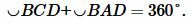 Следовательно
Следовательно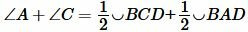
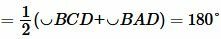
 .
.
 следует
следует 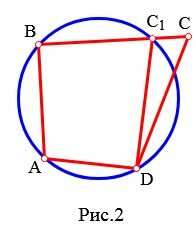
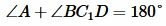 . Но по условию теоремы
. Но по условию теоремы 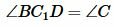 . С другой стороны, угол BC1D является внешним углом треугольника DC1C, т.е. выполняется равенство
. С другой стороны, угол BC1D является внешним углом треугольника DC1C, т.е. выполняется равенство 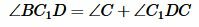 . Получили противоречие, следовательно точка C не может лежать вне окружности.
. Получили противоречие, следовательно точка C не может лежать вне окружности.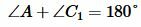 . Но по условию данной теоремы
. Но по условию данной теоремы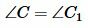 .
.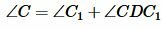 . Получили противоречие, следовательно точка C не может лежать внутри окружности.
. Получили противоречие, следовательно точка C не может лежать внутри окружности.