Апофема правильного четырехугольника пирамиды

Для успешного решения задач по геометрии необходимо четко понимать термины, которые использует эта наука. Например, таковыми являются «прямая», «плоскость», «многогранник», «пирамида» и многие другие. В данной статье ответим на вопрос, что такое апофема.

Видео:Нахождение апофемы пирамидыСкачать

Двоякое использование термина «апофема»

В геометрии значение слова «апофема» или «апотема», как ее еще называют, зависит от того, к какому объекту ее применяют. Существует два принципиально разных класса фигур, в которых она является одной из их характеристик.

В первую очередь это плоские многоугольники. Что такое апофема для многоугольника? Это высота, проведенная из геометрического центра фигуры к любой из ее сторон.

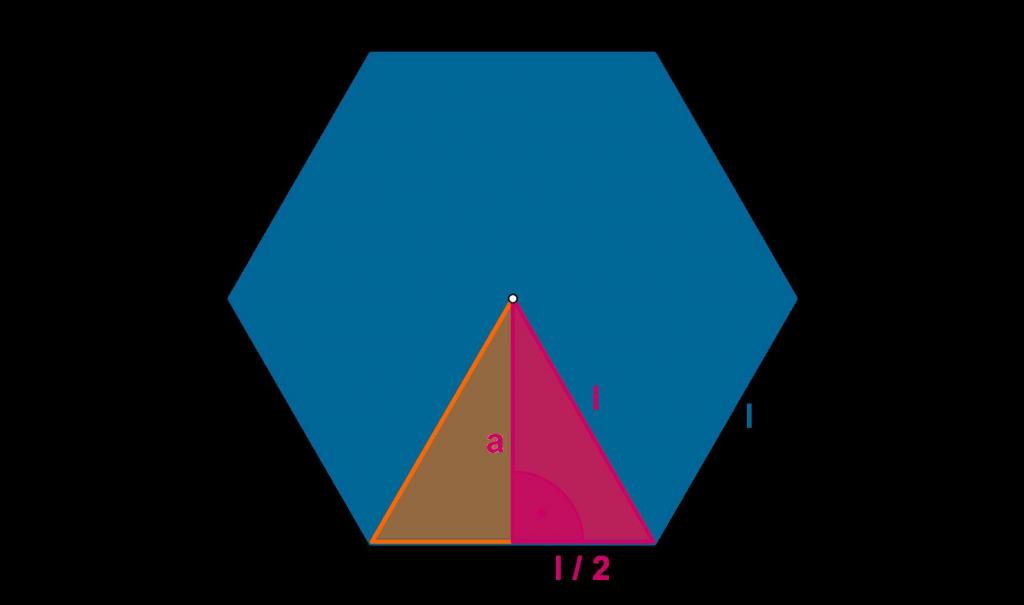
Чтобы было понятнее, о чем идет речь, рассмотрим конкретный пример. Предположим, что имеется правильный шестиугольник, показанный ниже на рисунке.

Символом l обозначена длина его стороны, буквой a — апофема. Для отмеченного треугольника она является не только высотой, но и биссектрисой, и медианой. Несложно показать, что через сторону l ее можно вычислить так:

Аналогичным образом апофема определяется для любого n-угольника.

Во вторую очередь — это пирамиды. Что такое апофема для такой фигуры? Этот вопрос требует более детального рассмотрения.

Видео:10 класс, 33 урок, Правильная пирамидаСкачать

Пирамиды и их апофемы

Для начала дадим определение пирамиде с точки зрения геометрии. Эта фигура представляет собой объемное тело, образованное одним n-угольником (основание) и n треугольниками (боковые стороны). Последние соединены в одной точке, которая называется вершиной. Расстояние от нее до основания — это высота фигуры. Если она попадает на геометрический центр n-угольника, то пирамида называется прямой. Если к тому же n-угольник имеет равные углы и стороны, то фигура называется правильной. Ниже показан пример пирамиды.

Что такое апофема для такой фигуры? Это перпендикуляр, который соединяет стороны n-угольника с вершиной фигуры. Очевидно, что она представляет собой высоту треугольника, являющегося боковой стороной пирамиды.

Апофему удобно использовать при решении геометрических задач с правильными пирамидами. Дело в том, что для них все боковые грани являются равными друг другу равнобедренными треугольниками. Последний факт означает, что все n апофем равны, поэтому для правильной пирамиды можно говорить об одной-единственной такой прямой.

Видео:Найти площадь поверхности правильной четырехугольной пирамидыСкачать

Апофема четырехугольной пирамиды правильной

Пожалуй, самым наглядным примером этой фигуры будет знаменитое первое чудо света — пирамида Хеопса. Она находится в Египте.

Для любой такой фигуры с правильным n-угольным основанием можно привести формулы, позволяющие определить ее апофему через длину a стороны многоугольника, через боковое ребро b и высоту h. Здесь запишем соответствующие формулы для прямой пирамиды с квадратным основанием. Апофема h_b для нее будет равна:

Первое из этих выражений справедливо для любой правильной пирамиды, второе — только для четырехугольной.

Покажем, как эти формулы можно использовать для решения задачи.

Видео:🔴 Найдите объём правильной четырёхугольной ... | ЕГЭ БАЗА 2018 | ЗАДАНИЕ 16 | ШКОЛА ПИФАГОРАСкачать

Геометрическая задача

Пусть задана прямая пирамида, имеющая квадратное основание. Необходимо рассчитать ее основания площадь. Апофема пирамиды равна 16 см, а ее высота в 2 раза больше стороны основания.

Каждый школьник знает: чтобы найти площадь квадрата, которым является основание рассматриваемой пирамиды, следует знать его сторону a. Для ее нахождения воспользуемся следующей формулой для апофемы:

Значение апофемы известно из условия задачи. Поскольку высота h в два раза больше длины стороны a, это выражение можно преобразовать следующим образом:

Площадь квадрата равна произведению его сторон. Подставляя полученное выражение для a, имеем:

Остается подставить в формулу значение апофемы из условия задачи и записать ответ: S ≈ 60,2 см 2 .

Видео:В правильной четырёхугольный пирамиде сторона основания равна 6, а высота 2 корня из 10. АпофемуСкачать

Апофема правильной пирамиды, формула

Апофема правильной пирамиды находится по формуле

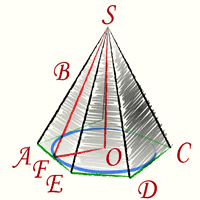f — апофема правильной пирамиды (SF)
n — число сторон правильного многоугольника — основания правильной пирамиды
a — сторона правильного многоугольника (AB или BC или CD или DE или EA) — основания правильной пирамиды
h — высота правильной пирамиды (OS)

Видео:КАК НАЙТИ ПЛОЩАДЬ БОКОВОЙ ПОВЕРХНОСТИ ПИРАМИДЫ?Скачать

Апофема правильной пирамиды выводится из следующих формул

Синим цветом на рисунке изображена вписанная в основание правильной пирамиды окружность. Треугольник SFO прямоугольный. Его стороны: OS — высота правильной пирамиды ( h), OF — радиус вписанной окружности в правильный многоугольник (основание правильной пирамиды ( r)), SF — апофема правильной пирамиды ( f). По теореме Пифагора

подставив сюда только радиус вписанной окружности получается формула (1).

Видео:Апофема правильной пирамиды. Задание А2 из ЦТ 2020 #цт2020Скачать

Апофема правильного четырехугольника пирамиды

Развернуть структуру обучения Свернуть структуру обучения Примечание. Это часть урока с задачами по геометрии (раздел стереометрия, задачи о пирамиде). Если Вам необходимо решить задачу по геометрии, которой здесь нет — пишите об этом в форуме. В задачах вместо символа «квадратный корень» применяется функция sqrt(), в которой sqrt — символ квадратного корня, а в скобках указано подкоренное выражение. Для простых подкоренных выражений может использоваться знак «√» . Теоретические материалы и формулы см. в главе «Правильная пирамида». Видео:АпофемаСкачать Задача Апофема правильной треугольной пирамиды равна 4см, а двугранный угол при основании равен 60 градусов. Найдите объем пирамиды. Поскольку пирамида правильная, учтем следующее: Высота пирамиды проецируется на центр основания Центр основания правильной пирамиды по условию задачи — равносторонний треугольник Центр равностороннего треугольника является одновременно центром вписанной и описанной окружности Высота пирамиды образует с плоскостью основания прямой угол Объем пирамиды можно найти по формуле: V = 1/3 Sh Поскольку апофема правильной пирамиды образует вместе с высотой пирамиды прямоугольный треугольник, для нахождения высоты используем теорему синусов. Кроме того, примем во внимание: Первый катет рассматриваемого прямоугольного треугольника является высотой, второй катет — радиусом вписанной окружности (в правильном треугольнике центр одновременно является центром вписанной и описанной окружности), гипотенуза является апофемой пирамиды Третий угол прямоугольного треугольника равен 30 градусам ( сумма углов треугольника — 180 градусов, угол 60 градусов дан по условию, второй угол — прямой по свойствам пирамиды, третий 180-90-60 = 30 ) синус 30 градусов равен 1/2 синус 60 градусов равен корню из трех пополам синус 90 градусов равен 1 Согласно теореме синусов: 4 / sin( 90 ) = h / sin ( 60 ) = r / sin( 30 ) 4 = h / ( √3 / 2 ) = 2r откуда r = 2 h = 2√3 В основании пирамиды лежит правильный треугольник, площадь которого можно найти по формуле: S правильного треугольника = 3√3 r 2 . S = 3√3 2 2 . S = 12√3 . Теперь найдем объем пирамиды: V = 1/3 Sh V = 1/3 * 12√3 * 2√3 V = 24 см 3 . Видео:Как найти апофему через площадь полной поверхности пирамиды? Ёфтани апофема аз рӯи масоҳати С.П. п-аСкачать Задача Высота и сторона основания правильной четырехугольной пирамиды соответственно равны 24 и 14. найдите апофему пирамиды. Поскольку пирамида правильная, то в ее основании лежит правильный четырехугольник — квадрат. Кроме того, высота пирамиды проецируется в центр квадрата. Таким образом, катет прямоугольного треугольника, который образован апофемой пирамиды, высотой и отрезком, их соединяющим, равен половине длины основания правильной четырехугольной пирамиды. Откуда по теореме Пифагора длина апофемы будет найдена из уравнения: 7 2 + 24 2 = x 2 x 2 = 625 x = 25 🌟 Видео АпофемаСкачать Правильная пирамида № 258Скачать Правильные многоугольники. Геометрия 9 класс | Математика | TutorOnlineСкачать 🙂 Площадь поверхности правильной пирамидыСкачать Искусственный интеллект требует жертв, или ЖКХ — это ад на землеСкачать Построение сечения пирамиды по трем точкамСкачать №258. Боковое ребро правильной четырехугольной пирамиды образует угол в 60° с плоскостью основания.Скачать №268. Плоскость, параллельная плоскости основания правильной четырехугольной пирамиды,Скачать Пирамида. 11 класс.Скачать 10 класс, 34 урок, Усеченная пирамидаСкачать Пересечение многогранников. Пирамида с призматическим вырезом.Скачать Поделиться или сохранить к себе: Смотрите также Является ли четырехугольник прямоугольником если все его углы равны все его стороны равны Является ли четырехугольник параллелограммом если сумма его соседних углов равна 180 градусам Является ли четырехугольник параллелограммом если сумма его соседних углов равна 180 degree180 Является ли четырехугольник параллелограммом если его противоположные углы равны да или нет Чья комната походила как будто на сарай имела неправильный вид четырехугольника Что можно сказать о четырехугольнике если серединные перпендикуляры пересекаются в одной точке Четырехугольники авсд и дсеф имеют общую сторону сд точки а д ф Четырехугольник является правильным если все его стороны равны и один из углов