25 могут ли все углы выпуклого четырехугольника быть а тупыми б острыми в прямыми

Геометрия | 5 — 9 классы

Могут ли все углы выпуклого четырехугольника быть тупыми.

Видео:Что такое угол? Виды углов: прямой, острый, тупой, развернутый уголСкачать

Один из углов выпуклого четырехугольника равен сумме двух других углов?

Один из углов выпуклого четырехугольника равен сумме двух других углов.

Докажите, что данный угол тупой.

Видео:№424. Докажите, что если не все углы выпуклого четырехугольника равны друг другуСкачать

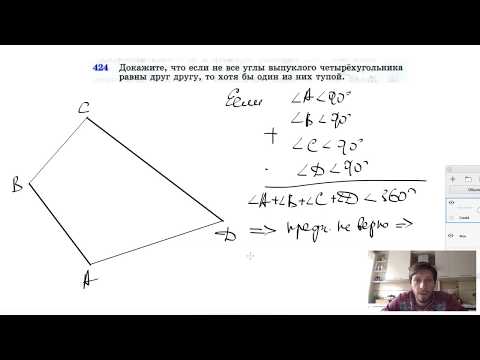
Чему равна сумма углов выпуклого четырехугольника?

Чему равна сумма углов выпуклого четырехугольника?

Видео:8 класс, 2 урок, Выпуклый многоугольникСкачать

Формула для вычисления суммы углов выпуклого четырехугольника?

Формула для вычисления суммы углов выпуклого четырехугольника.

Видео:8 класс, 3 урок, ЧетырехугольникСкачать

Может ли выпуклый чётырёхугольник иметь = три тупых угла?

Может ли выпуклый чётырёхугольник иметь = три тупых угла?

Два тупых и два прямых угла?

Видео:№370. Найдите углы выпуклого четырехугольника, если они пропорциональны числам 1, 2, 4, 5.Скачать

Сколько тупых углов может быть в выпуклом четырехугольнике ?

Сколько тупых углов может быть в выпуклом четырехугольнике ?

Видео:№369. Найдите углы A, B и C выпуклого четырехугольника ABCD, еслиСкачать

В каком выпуклом n — угольнике все углы могут быть : 1)острыми ; 2) прямыми ; 3)тупыми?

В каком выпуклом n — угольнике все углы могут быть : 1)острыми ; 2) прямыми ; 3)тупыми.

Видео:№368. Найдите углы выпуклого четырехугольника, если они равны друг другу.Скачать

Может ли выпуклый четырёхугольник иметь : 1)три тупых угла, б)два тупых и два прямых угла?

Может ли выпуклый четырёхугольник иметь : 1)три тупых угла, б)два тупых и два прямых угла?

ПРОШУ ВАС ПОМОГИТЕ ПЛИИИИЗ.

Видео:Сумма внутренних углов многоугольника. Выпуклые и невыпуклые многоугольники. 8 класс.Скачать

Чему равна сумма углов выпуклого четырехугольника?

Чему равна сумма углов выпуклого четырехугольника.

Видео:7 класс, 30 урок, Углы с соответственно параллельными или перпендикулярными сторонамиСкачать

Чему равна сумма углов выпуклого четырехугольника?

Чему равна сумма углов выпуклого четырехугольника.

Видео:№371. Докажите, что выпуклый четырехугольник ABCD является параллелограммом,Скачать

Может ли выпуклый четырехугольник иметь три острых угла?

Может ли выпуклый четырехугольник иметь три острых угла?

На этой странице сайта, в категории Геометрия размещен ответ на вопрос Могут ли все углы выпуклого четырехугольника быть тупыми?. По уровню сложности вопрос рассчитан на учащихся 5 — 9 классов. Чтобы получить дополнительную информацию по интересующей теме, воспользуйтесь автоматическим поиском в этой же категории, чтобы ознакомиться с ответами на похожие вопросы. В верхней части страницы расположена кнопка, с помощью которой можно сформулировать новый вопрос, который наиболее полно отвечает критериям поиска. Удобный интерфейс позволяет обсудить интересующую тему с посетителями в комментариях.

Высота равностороннего треугольника через его сторону : h = a√3 / 2, где а — сторона треугольника⇒ а = 2h / √3 = 2 * 9 * √3 / √3 = 18.

А — гипотенуза (и она жесторона равностороннеготреугольника) а / 2 — катет (половина основания равностороннего треугольника) h — катет (высотаравностороннего треугольника) По теореме Пифагора а² = (a / 2)² + h² a² — a² / 4 = h² 3 / 4 * a² = h² a² = 4..

90 градусов так как смежные углы дают в сумме 180 градусов.

Треугольник ABC — прямоугольный, гипотенуза AB = 10, катет AC = 8, тогда второй катет по теореме Пифагора BC² = AB² — AC² = 100 — 64 = 36 BC = 6.

При пересечении 2 — х прямых образуются 2 пары равных между собой углов. Называемых вертикальными. Если один из них 29 . Есть еще один такой же. А величину каждого из второй пары найдите вычитанием из 180 — ти 29 — ти.

180 — 91° — 72° = 17° ADC 17°.

Этот треугольник может быть равносторонним и равнобедренным.

Видео:Все типы 24 задание 2 часть ОГЭ ПО МАТЕМАТИКЕ 2023 УмскулСкачать

25 могут ли все углы выпуклого четырехугольника быть а тупыми б острыми в прямыми

Урок № 2

Тема. Выпуклые четырехугольники. Сумма углов четырехугольника

Цель: сформировать представление о внутреннюю область четырехугольника, понятие выпуклого и невыпуклого четырехугольников, угла выпуклого четырехугольника, соседних и противоположных углов выпуклого четырехугольника. Сформировать первичные умения:

· воспроизводить изученные определения;

· различать на готовых рисунках изученные объекты;

· изображать изученные объекты на рисунке.

Сформировать осознанное понимание содержания теоремы о сумме углов выпуклого четырехугольника и умение ее применять при решении задач.

Тип урока: усвоение новых знаний.

Наглядность и оборудование: конспект «Четырехугольники».

I. Организационный этап

II . Проверка домашнего задания

Для проверки усвоения учащимися содержания основных понятий, рассмотренных на предыдущем уроке, можно провести математический диктант.

1. Выполните изображение четырехугольника MNKP

Обозначьте на рисунке пару противоположных сторон

2. Как называются отрезки, соединяющие противоположные вершины четырехугольника?

2. Чем является в четырехугольнике конце его диагонали?

3. Какие из вершин четырехугольника АМОР являются соседними к вершине А?

3. Какие из сторон четырехугольника ВСКМ являются соседними в стороны КМ?

4. Одна из сторон четырехугольника вдвое больше каждой из других сторон. Зная, что периметр четырехугольника равен 40 см, найдите длину

большей из сторон

меньшей из сторон

III . Формулировка цели и задач урока

С целью лучшего осознания учащимися учебного материала урока целесообразно использовать прием аналогии. Для этого сравним определение треугольника и его элементов с обозначением четырехугольника и его элементов. Во время сравнения определений повторяем определение внутреннего угла треугольника и теорему о сумме всех его углов. Следовательно, возникает вопрос о существовании аналогичной теоремы о сумме внутренних углов четырехугольника. Ответ на этот вопрос и является основной дидактической целью урока.

IV . Актуализация опорных знаний

Выполнение устных упражнений по готовым рисункам

Дано: АВ = ВС, AD = DC .

Доказать: A = C

Доказать: C + D = 180°

Дано: 1 = 2, 3 = 4.

Доказать: AB = AD , BC = CD

Дано: АВ = А, D , С, B = С D .

Доказать: AC 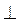BD

Дано: AB = DC , BC = AD .

Доказать: 1 = 2

V . Усвоение знаний

План изучения нового материала

1. Внутренняя область четырехугольника.

2. Выпуклый четырехугольник.

3. Внутренний угол выпуклого четырехугольника.

4. Свойство внутренних углов выпуклого четырехугольника.

@ Во время подготовки к изложению материала относительно понятия выпуклого четырехугольника по новому учебнику учителю следует обратить внимание на другой подход к изложению этого вопроса, а именно: сначала вводится понятие внутренней области четырехугольника (в дальнейшем используется для введения понятия площади многоугольника), а затем формируется представление о двух возможных случаях взаимного расположения прямой, содержащей сторону четырехугольника, относительно внутренней области четырехугольника: прямая или пересекает или не пересекает эту внутреннюю область. Далее на основе этого представления формируется понятие выпуклого (и невыпуклого) четырехугольника, которое закрепляется во время работы с готовыми рисунками. Что касается понятия угла выпуклого четырехугольника (внутреннего), а также теоремы о сумме углов выпуклого четырехугольника, то эти вопросы в новом учебнике освещаются по таким же принципам, как и в традиционных учебниках геометрии (как, в частности, в учебнике Геометрия. 7-9 / Под ред. О. В. Погорелова).

Задачи. На каком из приведенных рисунков изображен выпуклый четырехугольник (см. рис. 1)?

VI . Формирование умений и навыков

Выполнение устных упражнений

1. Могут ли все углы выпуклого четырехугольника быть острыми? тупыми? прямыми?

2. Может ли выпуклый четырехугольник иметь три острые углы? три тупые углы? две прямые углы? три прямые углы и один косвенный?

3. Могут ли углы треугольника равны трем углам четырехугольника? Ответ обоснуйте.

Выполнение графических упражнений

Проведите две параллельные прямые. Отметьте на одной из них точки А и D , а другие — точки В и С так, чтобы при последовательном соединении этих точек образовался четырехугольник ABCD .

а) является построенный четырехугольник выпуклым? Почему?

б) Измерьте внешние углы четырехугольника ABCD (по одному при каждой вершине) и вычислите их сумму.

Выполнение письменных упражнений

1. Два угла четырехугольника равны 80° и 100°, а два другие углы имеют равные градусные меры. Найдите наибольший угол четырехугольника.

2. Найдите углы четырехугольника, если один из них вдвое меньше второго, на 20° меньше третьего и на 40° меньше четвертого.

3. Периметры четырехугольников ABCD и ABCD 1 уровне. Может ли один из этих четырехугольников быть выпуклым, а второй — неопуклим? Ответ подтвердите рисунком.

VII . Итоги урока

Задачи. В приведенных утверждениях найдите и исправьте ошибку:

1) сумма углов любого четырехугольника равна 360°;

2) четырехугольником называется фигура, которая состоит из четырех точек, никакие три из которых не лежат на одной прямой, и четырех отрезков, последовательно соединяющих эти точки;

3) диагональ четырехугольника — это отрезок, соединяющий две вершины четырехугольника;

4) выпуклый четырехугольник — это четырехугольник, который не пересекается прямой.

VIII . Домашнее задание

Изучить содержание понятий, рассмотренных на уроке (см. конспект), и доказательства теоремы о сумме углов выпуклого четырехугольника. Решить задачи.

1. Найдите углы четырехугольника ABCD , если A = B , C = D , а сумма углов А и В равна 160°.

2. Найдите наименьший угол четырехугольника, если суммы его углов, взятых по три, равны 240°, 260° и 280°.

3. Если один из углов выпуклого четырехугольника — острый, то в этом четырехугольнике обязательно есть тупой угол. Докажите.

Видео:ОГЭ Задание 24 Площадь выпуклого четырехугольникаСкачать

В каком выпуклом n-угольнике все углы могут быть: а) острыми; б) прямыми; в) тупыми?

Видео:🔴 В выпуклом четырёхугольнике ABCD известно ... | ЕГЭ БАЗА 2018 | ЗАДАНИЕ 15 | ШКОЛА ПИФАГОРАСкачать

Ваш ответ

Видео:10 класс, 25 урок, Трехгранный уголСкачать

решение вопроса

Видео:№1,17 | Все теория по планиметрии за 4 часа | Решаем все прототипы №1 из ФИПИСкачать

Похожие вопросы

• Все категории
• экономические 43,277
• гуманитарные 33,618
• юридические 17,900
• школьный раздел 606,754
• разное 16,824

Популярное на сайте:

Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах.

Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте.

Как быстро и эффективно исправить почерк? Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.

Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью.

🎦 Видео

Что такое выпуклый четырёхугольник? | Математика 8 класс | Геометрия 8 класс | МегаШколаСкачать

Параллелограмм, прямоугольник, ромб,квадрат,трапеция, все свойства и определения!!!Скачать

Чему равна сумма углов выпуклого многоугольникаСкачать

Четырехугольники, вписанные в окружность. 9 класс.Скачать

7 класс Атанасян. Вся геометрия за 100 минут. Треугольник, окружность, задачи на построениеСкачать