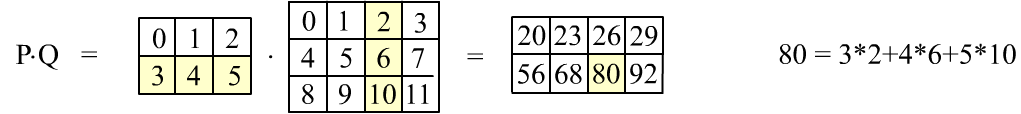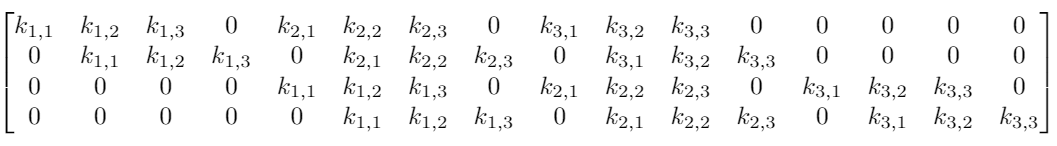Свертка матрицы в векторе

Видео:Матрицы и векторыСкачать

Введение

Данная статья является продолжением серии статей описывающей алгоритмы лежащие в основе
Synet — фреймворка для запуска предварительно обученных нейронных сетей на CPU.

Если смотреть на распределение процессорного времени, которое тратится на прямое распространение сигнала в нейронных сетях, то окажется что зачастую более 90% всего времени тратится в свёрточных слоях. Поэтому если мы хотим получить быстрый алгоритм для нейронной сети – нам нужен, прежде всего, быстрый алгоритм для свёрточного слоя. В настоящей статье я хочу описать методы оптимизации прямого распространения сигнала в свёрточном слое. Причем начать хочется с наиболее широко распространенных методов, основанных на матричном умножении. Изложение я буду стараться вести в максимально доступной форме, чтобы статья была интересна не только специалистам (они и так про это все знают), но и более широкому кругу читателей. Я не претендую на полноту обзора, так что любые замечания и дополнения только приветствуются.

Видео:Линал 2.6. Умножение матрицы на векторСкачать

Параметры свёрточного слоя

Начать описание хотелось бы с описания параметров, которые есть в свёрточном слое. Специалисты могут смело пропустить этот раздел.

Размеры входного и выходного изображения

Прежде всего, свёрточный слой характеризуется входным и выходным изображением, которые характеризуются следующими параметрами:

• srcC / dstC — число каналов во входном и выходном изображении. Альтернативные обозначения: C / D.
• srcH / dstH — высота входного и выходного изображения. Альтернативное обозначение: H.
• srcW / dstW — ширина входного и выходного изображения. Альтернативное обозначение: W.
• batch — число входных (выходных) изображений — слой за раз может обработать целую партию изображений. Альтернативное обозначение: N.

Размеры ядра свертки

Операция свертки по своей сути — это взвешенная сумма некой окрестности данной точки изображения. Размер ядра свертки — характеризует величину этой окрестности и описывается двумя параметрами:

• kernelY — высота ядра свертки. Альтернативное обозначение: Y.
• kernelX — ширина ядра свертки. Альтернативное обозначение: X.

Наиболее часто встречаются свертки с размером ядра 1×1 и 3×3. Размеры 5×5 и 7×7 встречаются значительно реже. Большие размеры свертки, а также свертки с ядром отличным от квадратного тоже иногда встречаются, но это больше экзотика.

Шаг свертки

Еще один важный параметр — шаг свертки:

• strideY — вертикальный шаг свертки.
• strideX — горизонтальный шаг свертки.

Если шаг отличен от 1×1, например — 2×2, то выходное изображение будет в два раза меньше (свертка будет рассчитана только в окрестности четных точек).

Растяжение свертки

Ядро свертки можно растянуть (увеличить эффективный размер окна, при сохранении количества операций) при помощи следующих параметров:

• dilationY — вертикальное растяжение свертки.
• dilationX — горизонтальное растяжение свертки.

Стоит отметить, что случаи с растяжением, отличным от 1×1 достаточно редкое явление (так я за свою карьеру с таким ни разу не встретился).

Паддинг входного изображения

Если применить свертку с окном, отличным от единичного к изображению, то выходное изображение будет меньше на величину kernel — 1. Свертка как бы «съедает» края. Чтобы сохранить размер изображения, входное изображение часто дополняют по краям нулями. За это отвечают еще четыре параметра:

• padY / padX — передние вертикальный и горизонтальный отступы.
• padH / padW — задние вертикальный и горизонтальный отступы.

Группы каналов

Обычно каждый выходной канал представляет собой сумму сверток по всем входным каналам. Однако, это не всегда так. Есть возможность разбить входные и выходные каналы на группы, суммирование осуществляется только внутри групп:

• group — число групп.

На практике чаще всего встречаются ситуации с group = 1 и group = srcC = dstC — так называемое depthwise convolution.

Смещение и активационная функция

Хотя формально смещение и активационная функция не входят в свертку, но очень часто эти две операции следуют за свёрточным слоем, почему их обычно тоже включают в него. В виду разнообразия возможных активационных функций и их параметров, я не буду здесь их подробно описывать.

Видео:ТЕНЗОРЫ ДЛЯ САМЫХ МАЛЕНЬКИХ ЧАЙНИКОВ (ДЛЯ ФИЗИКОВ)Скачать

Базовая реализация алгоритма

Для начала хотелось бы привести базовую реализацию алгоритма:

В этой реализации я предполагал, что входное и выходное изображение имеет формат NCHW:

веса свертки хранятся в формате DCYX, а активационная функция у нас это ReLU. В общем случае это не так, но для базовой реализации такие предположения вполне уместны — надо же от чего-то отталкиваться.

Мы имеем 8 вложенных циклов и общее количество операций:

при этом количество данных во входном:

Видео:Умножение матрицСкачать

ML: Тензоры в Numpy

Видео:Собственные значения и собственные векторы матрицы (4)Скачать

Введение

Тензор — это множество упорядоченных чисел ( элементов), пронумерованных при помощи d целочисленных индексов: $mathrm[i_0,, i_1,. , i_]$. Число индексов d называется размерностью тензора.
Каждый индекс меняется от 0, до $d_i-1$, где $d_i$ называется размерностью индекса.
Перечисление размерностей всех индексов: $(d_0,,d_1. d_)$ называется формой тензора.

Существующие фреймворки машинного обучения работают с тензорами примерно одинаковым образом.
Ниже мы рассмотрим универсальную библиотеку numpy. Это не справочник по numpy, для этого см. scipy.org.
Мы сосредоточимся на понятиях размерности и формы тензора, а также на том, как они изменяются при различных операциях (что собственно и требуется при анализе нейронных сетей).

Видео:Умножение матрицСкачать

Размерность и форма тензора

В библиотеке numpy у каждого тензора t есть четыре базовых свойства (атрибута):

• t. ndim — размерность = сколько у тензора индексов;
• t. shape — форма = кортеж с размерностью каждого индекса;
• t. size — количество элементов тензора (если shape=(a,b,c), то size=a*b*c);
• t. dtype — тип тензора ( float32, int32. ) одинаковый для всех элементов.

Если тензор имеет один индекс: t[i] — то это вектор ( ndim=1), а если у него два индекса: t[i,j] — то это матрица ( ndim=2). Индексы нумеруются начиная с нуля.

Метод np. array(lst) преобразует список lst (список чисел или список других списков) в тензор numpy:

Обратим внимание, что:

• форма одномерного тензора (вектора) это (n,) , а не (n) , т.к. для Python (n) — это число, а не кортеж.
• t = np.array( [[[1]]] ) — это тензор из одного числа, с shape=(1,1,1) и t.ndim==3, t[0,0,0]==1.

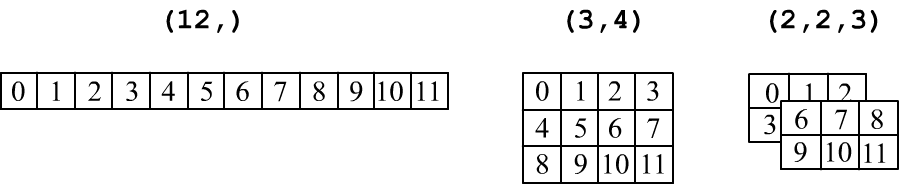
Тензоры принято изображать в табличной форме: вектор ( ndim=1) — это строка чисел, матрица формы (rows,cols) — это прямоугольная таблица с rows строчками и cols колонками. Трёхмерный тензор (три индекса, ndim=3) изображают в виде стопки матриц:

Важно не путать вектор (n,) и матрицу, состоящую из одной строки (1,n) или одной колонки (n,1):

Ниже матрицы из одной строчки или одной колонки окружены двойной линией, чтобы отличить их от вектора:

$$ begin hline 1 & 2\ hline end

begin hline begin hline 1 & 2\ hline end \ hline end

begin hline begin hline 1 \ hline 2\ hline end \ hline end $$

Видео:#11. Произведение матриц и векторов, элементы линейной алгебры | NumPy урокиСкачать

Последовательность элементов

Тензор формы shape = (a,b,c) состоит из size = a*b*c упорядоченных чисел (элементов).
Форму тензора можно изменить (с сохранением количества элементов size) при помощи метода reshape или прямого изменения атрибута shape:

$$ begin hline 1 & 2 & 3 & 4 & 5 & 6 \ hline end

begin hline begin hline 1 & 2 & 3 & 4 & 5 & 6 \ hline end\ hline end

begin hline 1 & 2 & 3 \ hline 4 & 5 & 6 \ hline end $$

При изменении формы тензора методом reshape, результат возвращается по ссылке (не создаётся новой копии множества чисел). Поэтому, если поменять значение элемента в m16, то он поменяется и в v:

Элементы в памяти идут в порядке увеличения индексов, начиная с конца. Например, для трёхмерного тензора с формой (2,1,3) это 6 чисел в следующем порядке:

Менять форму тензора можно произвольным образом, сохраняя неизменным число элементов. Ниже метод arange создаёт вектор (одномерный тензор) из 12 целых чисел от 0 до 11. Затем получаются ссылки на матрицу и трёхмерный тензор. В последнем случае значение -1 в размерности первого индекса, просит numpy самостоятельно высчитать эту размерность (исходя из числа элементов и размерностей остальных индексов):

Видео:Собственные векторы и собственные значения матрицыСкачать

Оси тензора

Индексы — это оси ( axis) тензора. Первый индекс — это axis=0, второй axis=1 и т.д. У многих методов есть параметр axis. Например, суммирование по данной оси уменьшает размерность ndim на 1.

Аналогично работают функции min, max, mean, median, var, std, argmin, argmax и т.п.

Из тензора можно вырезать подмножество его элементов. Ниже вырезается нулевая строчка и нулевая колонка, а затем квадратная матрица 2×2:

Подмножества элементов, находящиеся в v1, v2, v3 получаются по по ссылке, а не по значению, поэтому:

Менять можно не только значение одного элемента, но и всех элементов (ниже, стоящих в первой колонке):

Видео:Трехмерные линейные трансформации | Сущность Линейной Алгебры, примечаниеСкачать

Сложение, умножение и broadcasting

При поэлементном сложении и умножении тензоров одинаковой формы результат имеет ту же форму: $$ (x+y)_:

x_*y_. $$ Например (ниже np. arange(beg=0, end) — вектор целых чисел от beg до end, исключая end):

Аналогично работают функции от тензоров : $T’_=F(T_)$. Например: np. exp( ), np. log( ), np. sin( ), np. tanh( ), полный список см. на scipy.org.

При добавлении к матрице (n, m) вектора (n,) или матрицы, состоящей из одной строки (1,n), у последней дублируются строки и затем происходит сложение (или умножение) матриц одинаковой формы. При добавлении к матрице (n, m) матрицы, состоящей из одной колонки (m,1), у последней дублируются колонки: $$ begin hline 0 & 1 \ hline 2 & 3 \ hline end

begin hline mathbf & mathbf \ hline end

begin hline 0 & 1 \ hline 2 & 3 \ hline end

begin hline mathbf & mathbf \ hline mathbf & mathbf \ hline end,

begin hline 0 & 1 \ hline 2 & 3 \ hline end

begin hline begin hline mathbf \ hline mathbf \ hline end \ hline end

begin hline 0 & 1 \ hline 2 & 3 \ hline end

begin hline mathbf & mathbf \ hline mathbf & mathbf \ hline end $$

Например: В общем случае, для тензоров с различными shape, работает алгоритм расширения ( broadcasting):

• выравнивается число индексов ( ndim), добавляя к меньшему в shapeспереди единицы;
• размерности индексов считаются сравнимыми если они равны или один из них 1;
• размерность единичного индекса увеличиваем до большего, дублируя значения по этой оси:

Например, сложим матрицу из одной колонки и вектора $(3,1) + (2,) = (3,1) + (underline2) = (3,2)$: $$ beginhline beginhline 1\ hline 2\ hline 3\ hline end \ hline end

begin hline 4 & 5 \ hline end

begin hline begin hline 1\ hline 2\ hline 3\ hline end \ hline end

begin hline begin hline 4 & 5 \ hline end \ hline end

begin hline 1 & 1 \ hline 2 & 2 \ hline 3 & 3 \ hline end

begin hline 4 & 5 \ hline 4 & 5 \ hline 4 & 5 \ hline end

begin hline 5 & 6 \ hline 6 & 7 \ hline 7 & 8 \ hline end $$

Видео:МАТРИЦЫ математика УМНОЖЕНИЕ МАТРИЦ и простейшие операции с матрицамиСкачать

Свёртка векторов и матриц

В numpy обе операции выполняются при помощи метода dot. Так, для векторов:

Для матриц: Представим последнее умножение в табличном виде:

При матричном умножении сворачиваются строки первой матрицы со столбцами второй.
На рисунке выше приведено вычисление элемента $80$, закрашенного желтым цветом.
Чтобы получить все элементы, сначала первая строка первой матрицы должна 4 раза свернуться с 4-я колонками второй матрицы. Это даёт первую строку результирующей матрицы. Затем то-же делает вторая строка, что приводит ко второй строке результата.

Свёртка матриц возможна только, когда число колонок первой матрицы равно числу строк второй.
Выполняется следующая важная формула для форм исходных матрицы и результата свёртки:

$$ (n,, underline) cdot (underline, m)

Если первая матрица состоит из одной строчки, а вторая из одного столбика, то их произведение будет по-прежнему матрицей, но с одним элементом $(1,,underline)cdot(underline,,1)=(1,,1)$:

$$ begin hline begin hline 1 & 2\ hline end \ hline end

begin hline begin hline 3\ hline 4\ hline end \ hline end

Свёртка по единственному индексу: $(2,,underline) cdot (underline,,2) = (2,,2)$ равна попарному перемножению элементов (по тому же правилу «строка на столбец»): $$ begin hline begin hline 1\ hline 2\ hline end \ hline end

begin hline begin hline 3 & 4\ hline end \ hline end

begin hline 3 & 4 \ hline 6 & 8 \ hline end = c_r_ $$

Видео:Собственные векторы и собственные числа линейного оператораСкачать

Транспонирование матриц

Операция транспонирования переставляет элементы таким образом, что столбцы и строчки меняются местами. Если форма исходной матрицы была $(n,,m)$, то у транспонированной она будет $(m,,n)$:

begin hline 0 & 1 & 2 \ hline 3 & 4 & 5 \ hline end

begin hline 0 & 3 \ hline 1 & 4 \ hline 2 & 5 \ hline end $$

В numpy транспонирование осуществляется методом transpose() или при помощи атрибута .T:

Подчеркнём что транспонирование и перестановка размерностей при помощи reshape приводят к различному порядку элементов:

Транспонирование не создаёт новой матрицы (возвращается ссылка, а не значения). Поэтому:

Не квадратную матрицу можно умножить саму на себя, только предварительно транспонировав её (иначе не выполнится правило совпадение числа колонок и числа строк):

Для тензоров произвольной размерности операция транспонирования переставляет все индексы в противоположном порядке $t^T_=t_$: Как и в случае с матриц, такая перестановка индексов приводит иному порядку элементов, чем просто изменение атрибута shape.

Видео:Что такое векторы и матрицы? Душкин объяснитСкачать

Перемножение тензоров со свёрткой

Произведение вектора $mathbf$ и тензора $mathbf$, независимо от ndim последнего, интерпретируется следующим образом.
У тензора берутся последние два индекса и делаются такие свёртки (второй случай — по принципу «последний с предпоследним»):

mathbf cdot mathbf

Если у тензора ndim=2 (матрица), то вектор справа превращается в столбик, а слева — в строчку:

$$ begin hline 1 & 1 \ hline end cdot begin hline 1 & 1 & 1\ hline 1 & 1 & 1\ hline end cdot begin hline 1 \ hline 1 \ hline 1 \ hline end

6 $$ В этом случае для форм имеем: $underline,. (3,) = (3,),. (3,) = $ скаляр или $(2,),. underline = (2,),. (2,) = $ тот же скаляр.

Видео:4. Умножение матриц, примеры с решениемСкачать

Другие операции свёртки

Существует ещё один метод свёртки matmul (и @ — операция для него). Для ndim = 2 результат такой свёртки не отличается от свёртки dot. Различия начинаются при ndim > 2.

В этом случае тензоры интерпретируются как стопки 2D матриц по последним двум индексам.
Эти 2D матрицы перемножаются независимо в каждой «плоскости стопки».
Последние два индекса тензоров фиксируются, а по остальным тензоры расширяются (broadcasting).
Для векторов индекс добавляется, а потом убирается. $$ (overline, 2, 3)

(3, 2, 2, underline)

(3, 2, underline, 5)

(3, 2, 2, 5) $$ Перемножить $(mathbf,

5)$ нельзя, т.к. они нерасширяемы по «жирным» индексам (по последним двум индексам должно быть матричное умножение и их не трогаем). Как и в dot, размерность последнего индекса первого тензора и предпоследнего второго должны совпадать.

Универсальная свёртка np. tensordot(A, B, axes = (axes_A, axes_B)) проводит свёртку вдоль указанных индексов тензоров A и B:

Если axes = 1, то это стандартное dot — произведение. Если axes = 0, то это прямое произведение $Aotimes B$.

Видео:Умножение матриц как композиция | Сущность Линейной Алгебры, глава 4Скачать

Инициализация элементов

Инициализация элементов тензора может быть самой разнообразной. Для следующих методов элементы будут иметь тип float64: Следующие функции приводят к целочисленным элементам int32: Тип элементов этих тензоров зависит от аргументов методов инициализации:

Тип элементов можно менять в процессе инициализации:

Видео:Что такое вектора? | Сущность Линейной Алгебры, глава 1Скачать

Случайные тензоры

Видео:Занятие 12. Векторы и матрицыСкачать

Разные полезности

Пусть надо отобрать элементы, удовлетворяющие условию: Ещё одна возможность: numpy.where(condition, x[, y]) — из x или y:

Пусть есть два массива, элементы которых нужно синхронно перемешать:

Число значащих цифр и другие свойства вывода тензоров на печать задаются методом:

Видео:Матрицы: начало. Высшая математикаСкачать

Наглядно объясняем операцию свертки в моделях глубокого обучения

При помощи анимированных изображений и визуализаций слоев CNN-сетей раскрываем широко применяемое в моделях глубокого обучения понятие свертки.

В современных фреймворках глубокого обучения сверточные слои в моделях нередко представляются в виде однострочного кода. Само же понятие свертки обычно остается для начинающих аналитиков труднодоступным, как и лежащие в его основе понятия ядра, фильтра, канала и т. д. Тем не менее, свертка представляет собой мощный и расширяемый инструмент, позволяющий разреживать взаимодействия нейронов, находить общие параметры, работая одинаковым образом со входными данными различного размера. Сравним механики операции свертки и полносвязной нейросети.

Видео:Матрица линейного оператора (01)Скачать

Суть операции свертки на примере черно-белых изображений

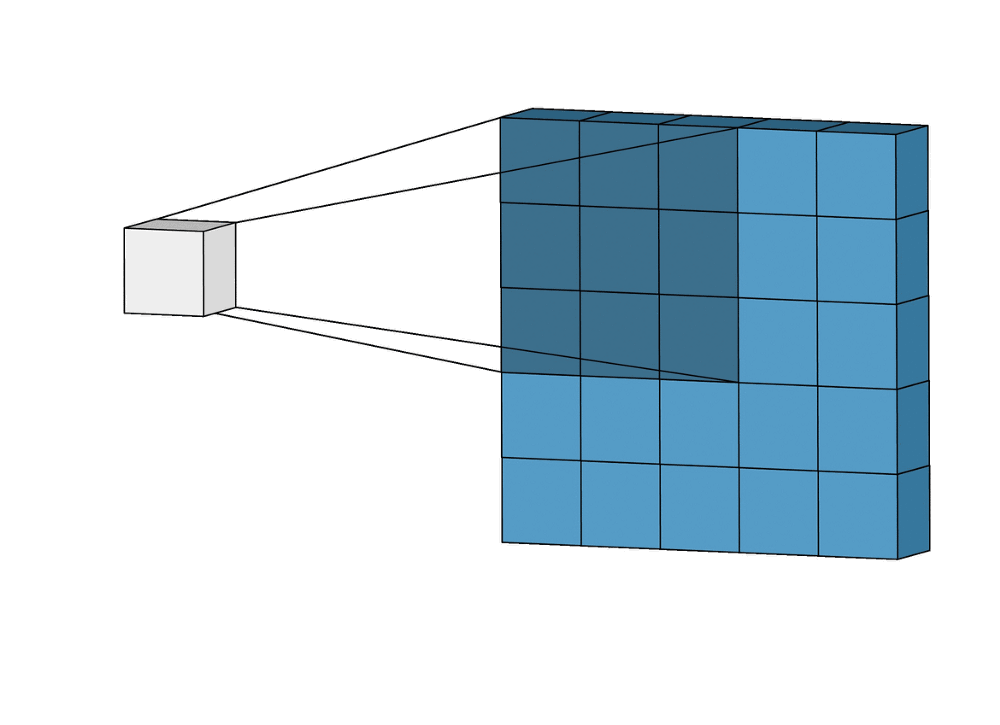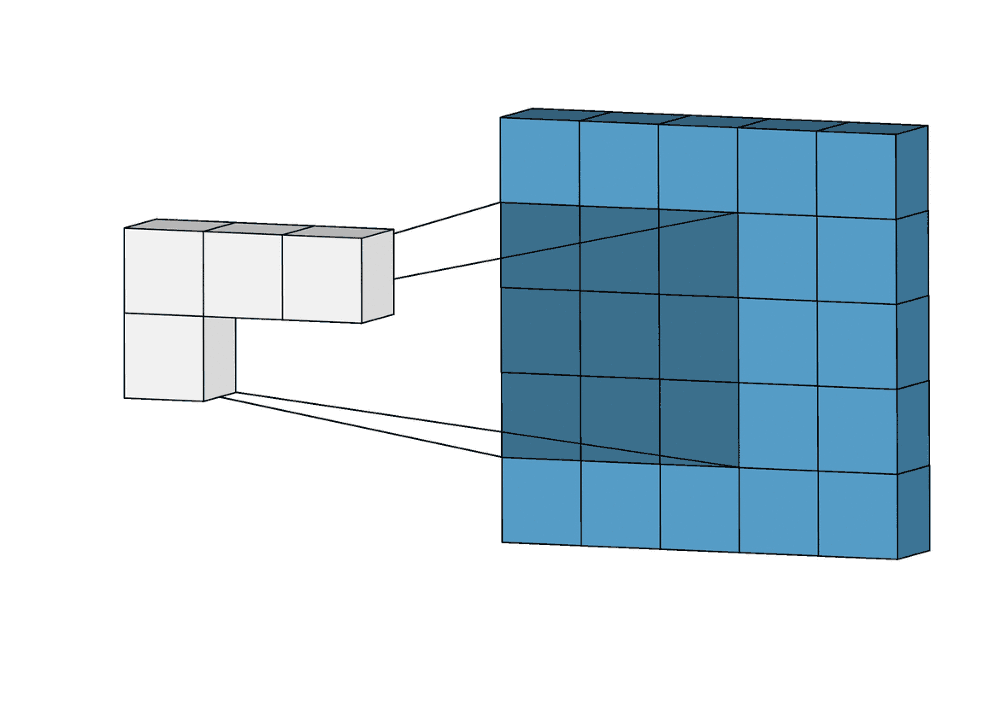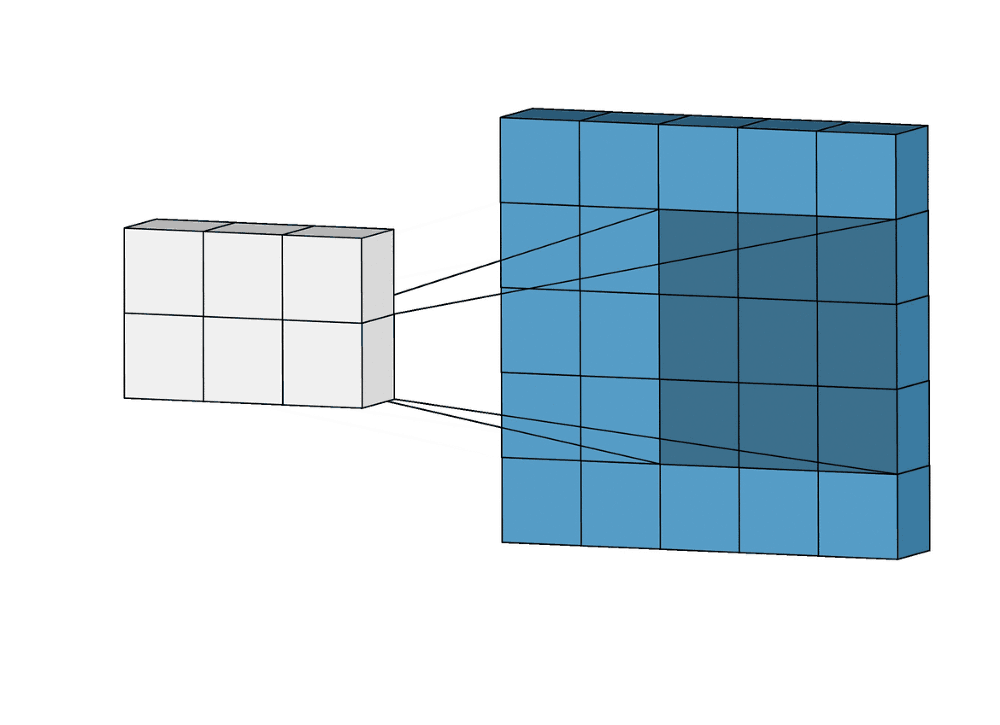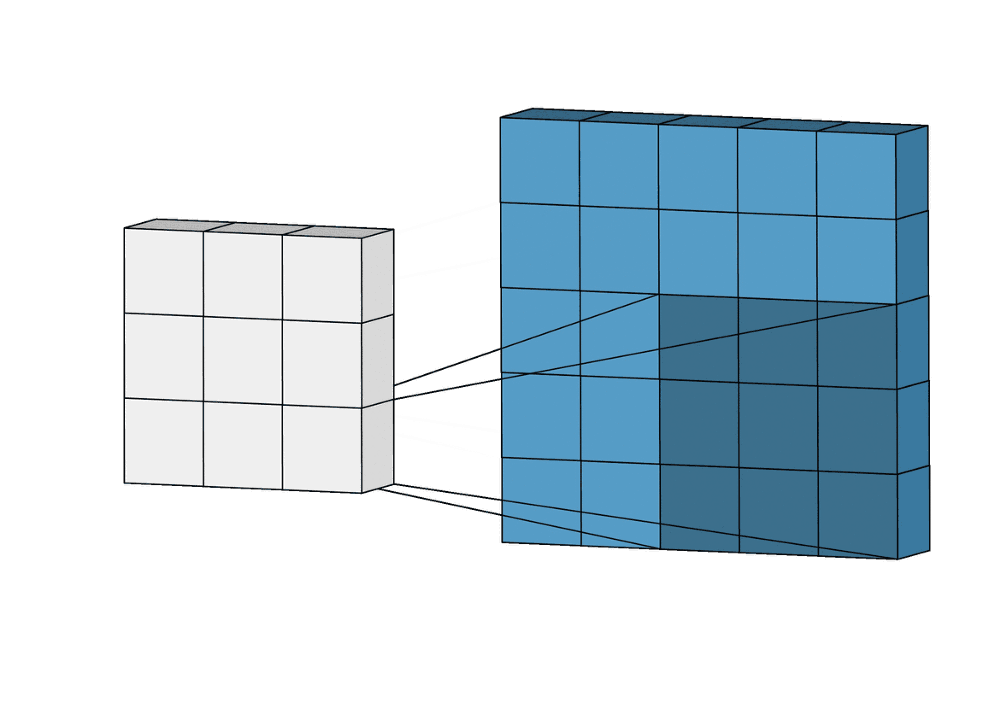
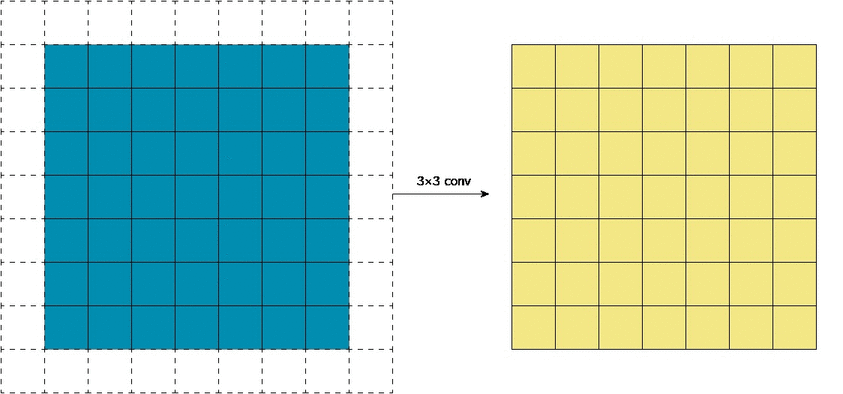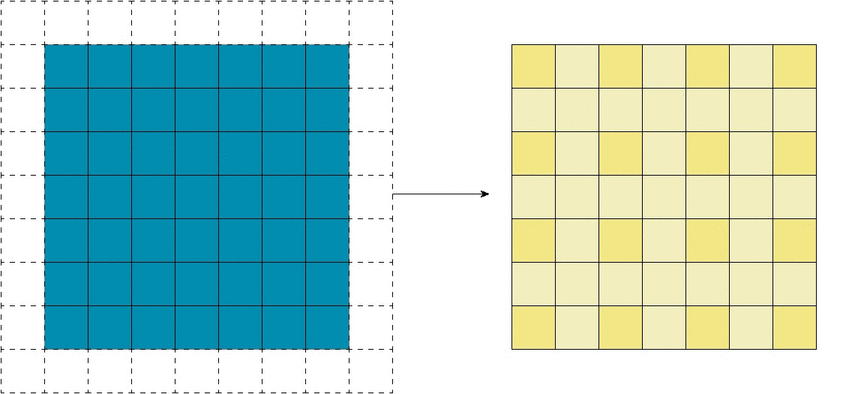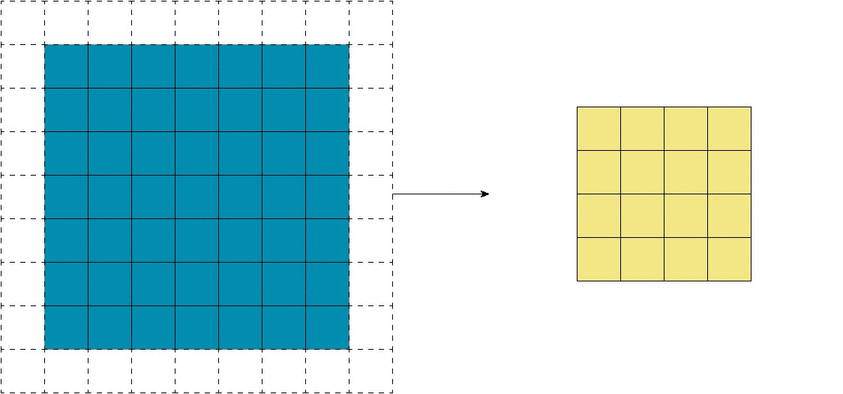
В математическом отношении в двумерной свертке нет ничего сложного. Имеется ядро – небольшая матрица весов. Это ядро «скользит» по двумерным входным данным, выполняя поэлементное умножение для той части данных, которую сейчас покрывает. Результаты перемножений ячеек суммируются в одном выходном пикселе. В случае сверточных нейросетей ядро определяется в ходе обучения сети. Начальные веса, аналогично случаю перцептрона, могут иметь рандомные значения, и корректируются в процессе обучения.

Перемножение и суммирование повторяются для каждой локации, по которой проходит ядро. Двумерная матрица входных признаков преобразуется в двумерную матрицу выходных. Выходные признаки, таким образом, являются взвешенными суммами входных признаков. Число входных признаков в комбинации для одного выходного признака определяет размер ядра.

Такой подход контрастирует с полносвязными сетями. Так, в приведенном выше примере имеется 5×5=25 входных признаков и 3×3=9 выходных. Если бы это были два полносвязных слоя, весовая матрица состояла бы из 25×9=225 весовых параметров. При этом каждая функция вывода была бы взвешенной суммой всех входов. В случае свертки, взвешенная сумма берется только по числу весов ядра. И в рассмотрении одновременно участвуют только близлежащие элементы.

Свертка соответствует модели иерархий абстрактных представлений: совокупность пикселей обобщается до ребер, те – до паттернов, и, наконец, до самого объекта. Малозначимые детали отфильтровываются в процессе перехода к более абстрактным образам.

Видео:Линейные трансформации и матрицы | Сущность Линейной Алгебры, глава 3Скачать

Некоторые распространенные методы

Обратим внимание на два характерных метода, связанных с операцией свертки: дополнение отступа (padding) и выбор шага (strides).

Нулевой отступ

В вышеприведенном примере скольжение ядра «обрезает» исходный двумерный массив по краю, преобразуя матрицу 5×5 в 3×3. Краевые пиксели теряются из-за того, что ядро не может распространяться за пределы края. Однако иногда необходимо, чтобы размер выходного массива был тем же, что и у входных данных.

Чтобы решить эту задачу, исходный массив можно дополнить «поддельными» пикселями. Например, в виде краевого поля, окружающего массив. Если в качестве значений берутся нули, говорят о «нулевом отступе» (zero padding).

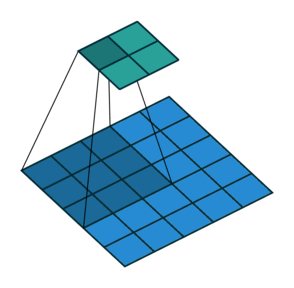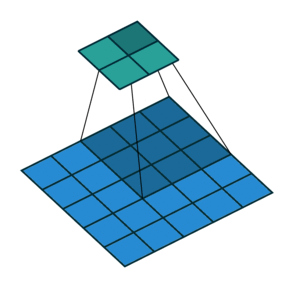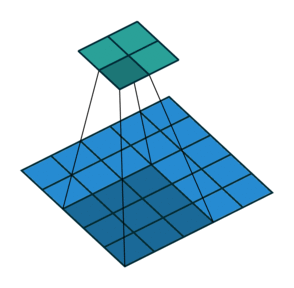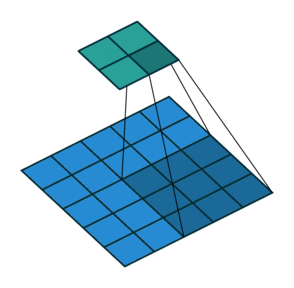
Еще чаще стоит задача субдискретизации – уменьшения размерности выходного сигнала в сравнении с исходным. Это обычное явление в сверточных нейросетях, где размер пространственных измерений уменьшается при увеличении количества каналов. Одним из способов является применение объединяющего (pooling) слоя. За счет отбора средних/максимальных значений из каждых соседствующих счетверенных ячеек 2×2 можно уменьшить размерность исходной сетки вдвое. Другой подход – использовать шаг свертки.

Идея шага состоит в том, чтобы при скольжении ядра пропускать часть позиций массива. Значения шага 1 означает выбор каждого пикселя сетки. Шаг 2 означает отбор пикселей на расстоянии в два пикселя с пропуском одного промежуточного, и так далее.

Видео:Линейная алгебра, 2 урок, Умножение матрицСкачать

Многоканальная версия – цветные изображения

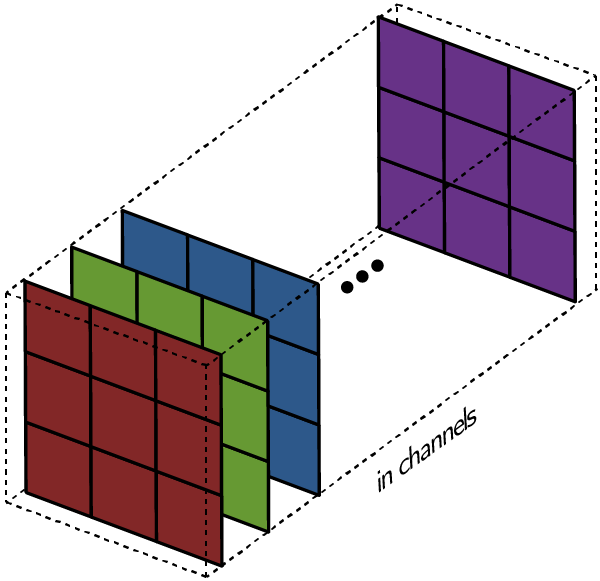
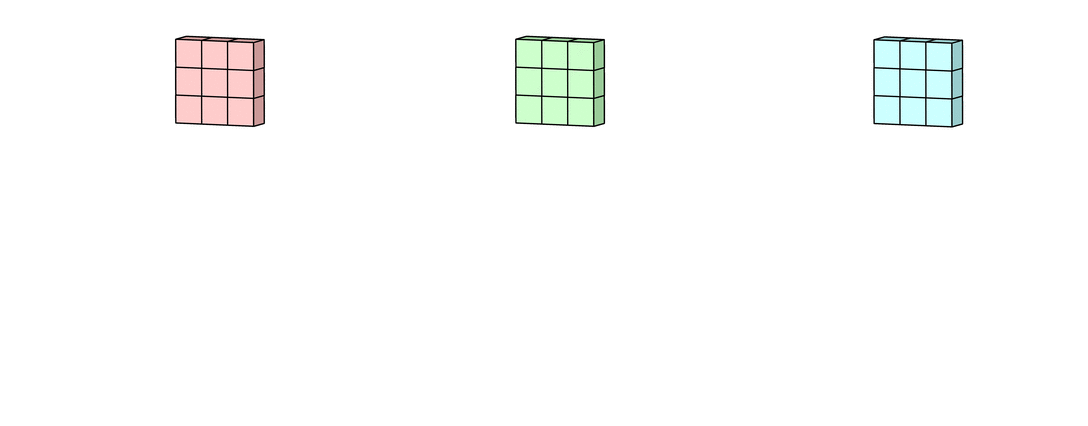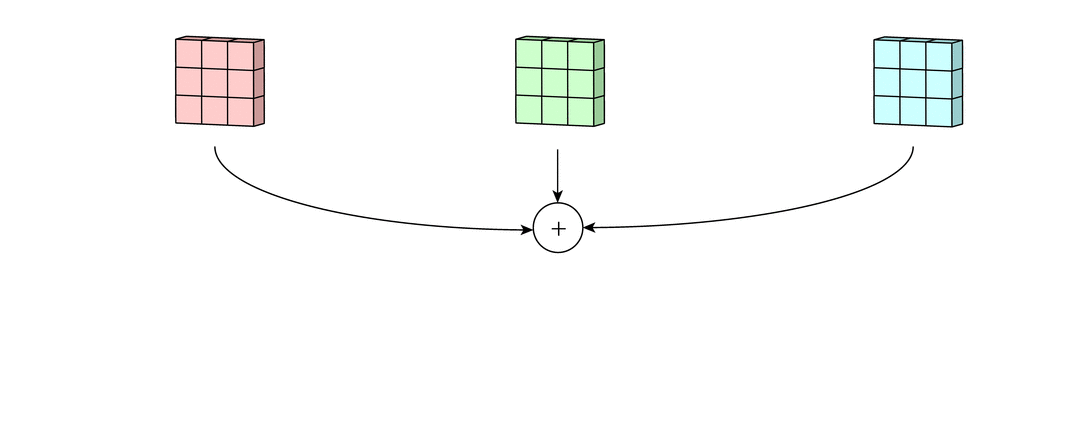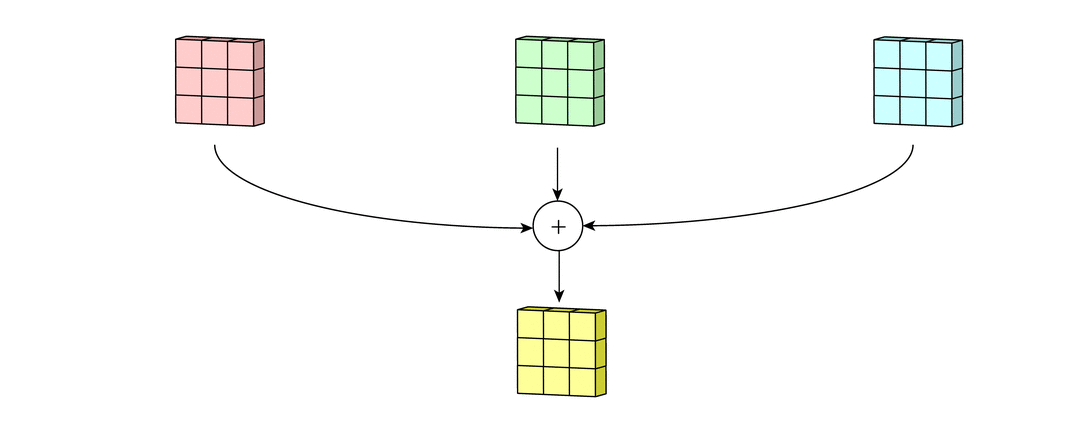
Вышеприведенные диаграммы соответствуют лишь изображениям с одним входным каналом. На практике большинство изображений имеют три канала: красный, зеленый и синий.

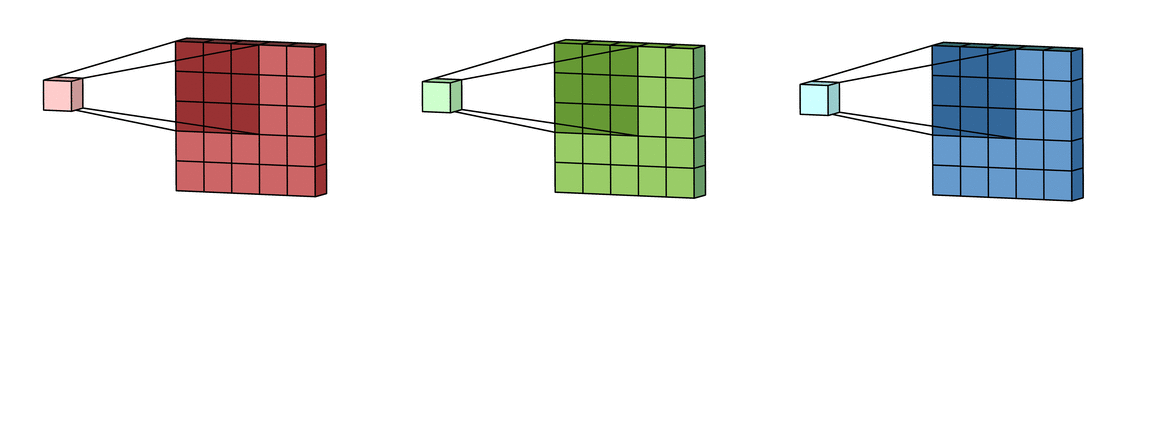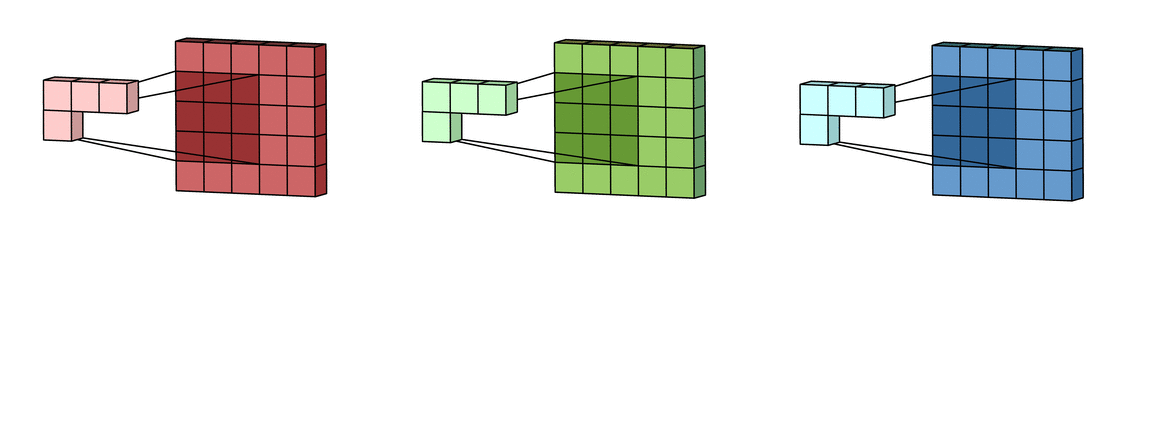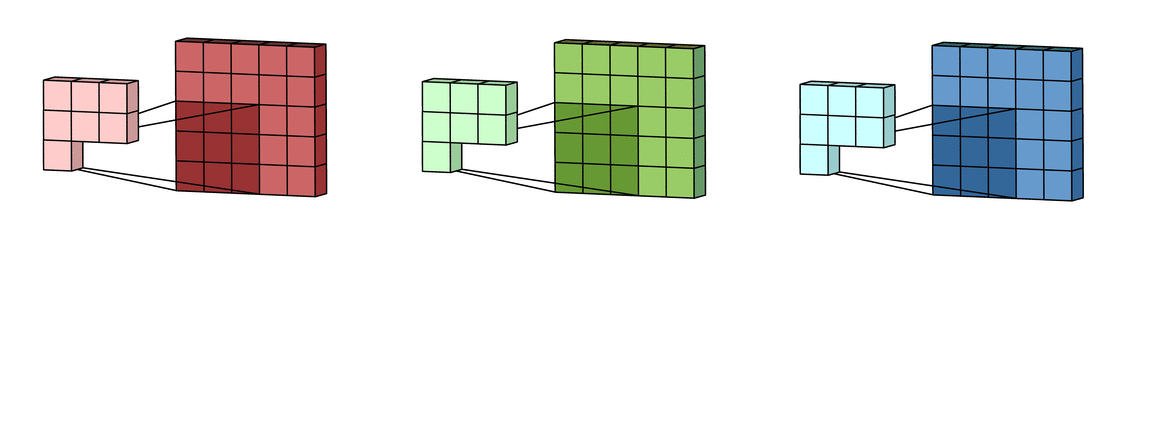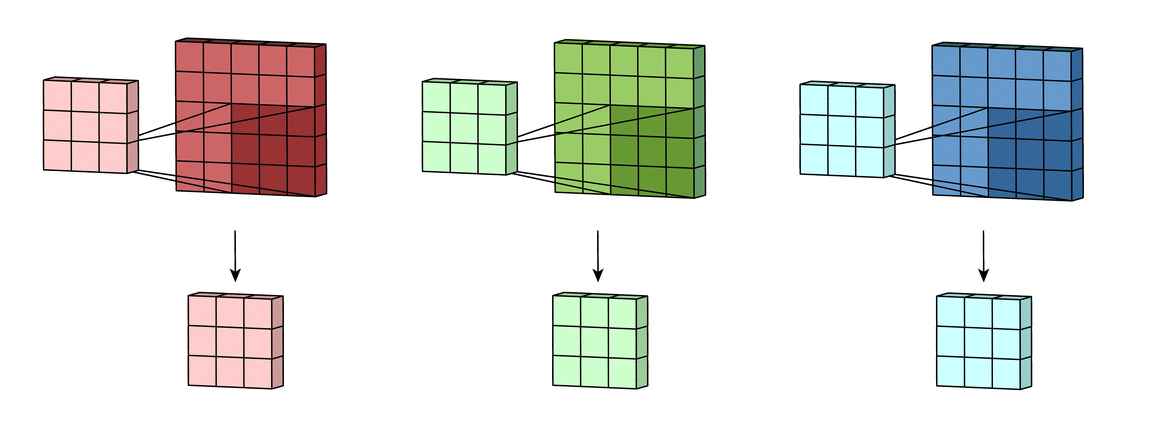
В случае с одним каналом термины фильтр и ядро взаимозаменяемы. Для цветного изображения они различны. Фильтр – это коллекция ядер, каждое из которых соответствует одному каналу. Ядро фильтра скользит по данным канала, создавая их обработанную версию. Значимость ядер определяется взаимным отношением их весов. Например, ядро для красного канала может быть более значимым в модели, чем другие ядра фильтра, тогда будут больше и соответствующие веса.

Каждая из обработанных в своих каналах версий суммируется для формирования общего канала.

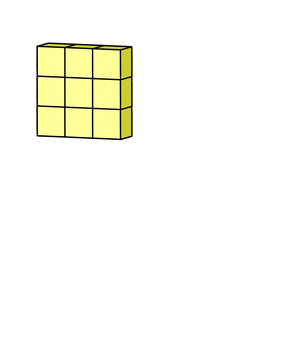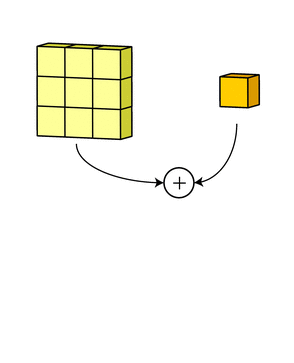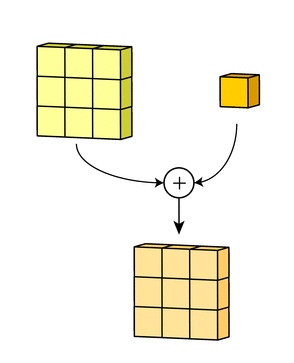
В выходном терминале может присутствовать линейное смещение, независимое от функций каждого из ядер и свойственное лишь выходному каналу.

Математическая подоплека свертки – особенности линейного преобразования

Предположим, что у нас есть вход 4×4. Мы хотим преобразовать его в сетку 2×2. Если мы используем сеть прямого распространения, потребуется входной вектор из 16 нейронов, полностью связанных с 4 выходными нейронами. Такую ситуацию можно визуализировать весовой матрицей w.

Хотя операция ядерной свертки может показаться вначале немного странной, она является линейным преобразованием. Если бы мы использовали ядро K размера 3 для тех же размеров входа и выхода, эквивалентная матрица линейного преобразования выглядела бы следующим образом:

Для матрицы с 16×4=64 элементами имеется всего 9 нетривиальных параметров, подлежащих оптимизации вместо 64 весовых параметров для полносвязной двухслойной нейронной сети. Обнуление значительной части параметров обусловлено локальностью применяемой операции. Помимо ускорения расчетов, свертка приводит и к лучшей инвариантности относительно размеров входных данных.

Впрочем это не объясняет, почему такой подход может быть не менее эффективным, чем полносвязная сеть. Ядро, формирующее выходной сигнал, представляет взвешенную комбинацию небольшой области близкорасположенных пикселей. Но в то же время операция взаимодействия с ядром применяется одинаково ко всему изображению.

Локальность свертки

Если бы это был какой-то другой тип данных, а не изображения (например, набор категориальных данных), обобщение, осуществляемое сверткой, могло бы привести к катастрофе. В выходных признаках появлялась бы отсутствовавшая исходно корреляция.

В то же время любое изображение с точки зрения математики представляет собой совокупность правил взаимного расположения элементов. Использование фильтров для поиска элементов изображений – это одна из старых идей компьютерного зрения. Например, для обнаружения контуров можно использовать фильтр Собеля. В отличие от обучаемых ядер сверточных нейронных сетей, ядро этого фильтра имеет фиксированные веса:

Для фонового неба, не содержащего краевых элементов большинство пикселей на изображении имеют одинаковые значения. Суммарные значения выхода ядра в этих местах равны нулю. Для части изображения с вертикальными границами в местах границ существует разница между пикселями слева и справа от края. Ядро, вычисляя эту ненулевую разницу, определяет положение контуров. Повторимся, ядро работает каждый раз только с локальными областями 3×3, обнаруживая аномалии в локальном масштабе.

Применяя один и тот же подход ко всему изображению, можно получить результат для всего массива. Аналогично свертка с транспонированным ядром позволяет выделить горизонтальные края.

Визуализация признаков при помощи оптимизации

Целая отрасль исследований в сфере глубокого обучения посвящена тому, чтобы сделать модели нейронных сетей интерпретируемыми. Одним из мощных инструментов для подобного рода задач является предложенная в работе 2017 года визуализация признаков при помощи оптимизации. Идея в корне простая: оптимизировать изображение, инициализированное шумом, так, чтобы активировать фильтр как можно сильнее.

На трех изображениях ниже представлены визуализации трех различных каналов для первого сверточного слоя GoogleNet. Хотя слои детектируют различные типы контуров, все они являются низкоуровневыми детекторами.

На двух следующих изображениях представлены примеры визуализации фильтров сверточных слоев второго и третьего уровней.

Одна из важных вещей: изображения после операции свертки – это все еще изображения. Операция действует эквивариантно: если изменяется вход, то выход изменяется так же.

Элементы, находившиеся в левом верхнем углу, после свертки имеют соответствующие отображения также в левом верхнем углу. Как бы глубоко ни заходили детекторы признаков, они все равно будут работать на очень маленьких ядерных участках. Неважно, насколько глубоко происходит свертка, но вы не можете обнаружить лица из сеток размером 3х3. Здесь возникает идея локальной зоны восприимчивости (receptive field).

Зона восприимчивости свертки

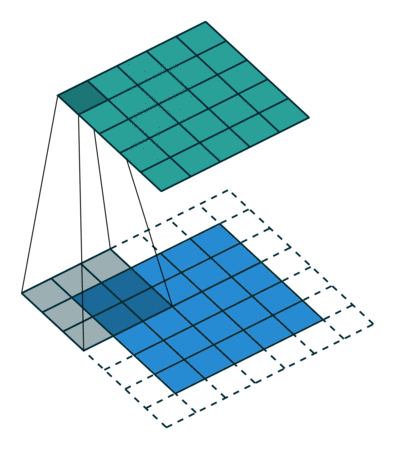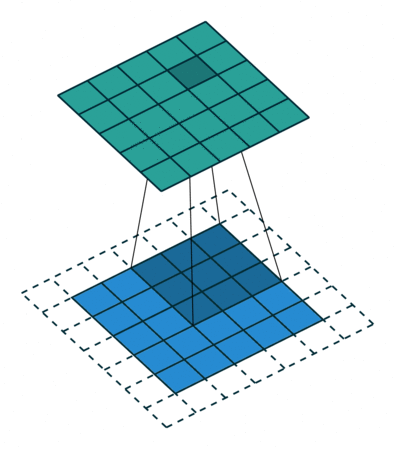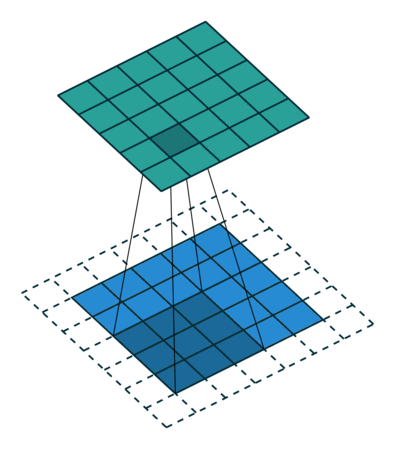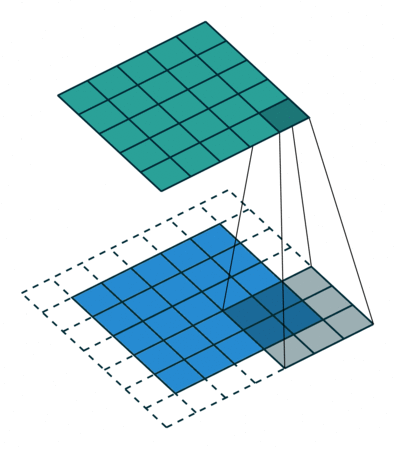
Существенной составляющей архитектуры сверточной нейронной сети является уменьшение объема данных от входа к выходу модели с одновременным увеличением глубины канала. Как упоминалось ранее, обычно это делается при помощи выбора шага свертки или pooling-слоев. Зона восприимчивости определяет, какая площадь оригинальных входных данных из исходной сетки обрабатывается на выходе. На изображениях ниже представлен пример шагающей свертки с выкидыванием промежуточных пикселей.

Ниже представлены примеры визуализации признаков набора блоков свертки, показывающие постепенное увеличение сложности. Расширение поля восприимчивости позволяет сверточным слоям комбинировать низкоуровневые признаки (линии, края) в более высокоуровневые (кривые, текстуры).

Сеть развивается от небольшого количества низкоуровневых фильтров на начальных этапах (64 в случае GoogleNet) до очень большого количества фильтров (1024 в финальной свертке), каждый из которых находит специфичный высокоуровневый признак. Переход от уровня к уровню обеспечивает иерархию распознавания образов.

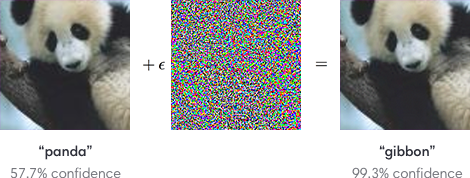
Обобщающие процессы свертки имеет свою оборотную сторону – возможность подделки изображений под удовлетворение особенностей распознающих фильтров. На изображениях ниже человек в обоих случаях узнает фотографии панды. А сверточные нейросети можно запутать, добавив шум, подстроенный под фильтры распознавания других образов.

Однако именно сверточные нейронные сети позволили компьютерному зрению пройти путь от простых приложений до сложных продуктов и услуг, таких как распознавание лиц и улучшение качества медицинских диагнозов.