Правильный треугольник — это треугольник, у которого
все стороны и углы равны.
Правильный треугольник, также называют равносторонним
и равноугольным. Все углы в таких треугольника имеют
градусную меру в 60 градусов.
Периметр правильного треугольника — это периметр
треугольника, у которого все стороны и углы равны.
Периметр в правильном треугольнике, можно найти с
помощью площади, длины сторон, радиуса и так далее.
Видео:Периметр треугольника. Как найти периметр треугольника?Скачать

Формула периметра
правильного треугольника
- Формула периметра правильного треугольника, через сторону:
Формула периметра правильного треугольника, через радиусвписанной окружности:
Формула периметра правильного треугольника, через радиус описанной окружности:
Формула периметра правильного треугольника, через площадь:
С помощью этих формул можно найти периметр через площадь,
сторону, радиус вписанной и описанной окружностей.
Видео:Правильные многоугольники. Геометрия 9 класс | Математика | TutorOnlineСкачать

Как найти периметр треугольника
О чем эта статья:
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Видео:Периметр правильного шестиугольника равен 150. Найдите диаметр описанной около него окружности (ЕГЭ)Скачать

Определение
Периметром принято называть длину всех сторон многоугольника. Периметр обозначается заглавной латинской буквой P. Под «P» удобно писать маленькими буквами название фигуры, чтобы не запутаться в задачах и ходе решении.
Важно, чтобы все параметры были переданы в одной единице длины, иначе мы не сможем подсчитать результат. Поэтому для правильного решения необходимо перевести все данные к одной единице измерения.
В чем измеряется периметр:
Видео:Всё про углы в окружности. Геометрия | МатематикаСкачать

Как узнать периметр треугольника
Рассмотрим какие существуют формулы, и при каких известных исходных данных их можно применять.
Если известны три стороны, то периметр треугольника равен их сумме. Этот способ проходят во втором классе.
P = a + b + c, где a, b, c — длина стороны.
Если известна площадь и радиус вписанной окружности:
P = 2 * S : r, где S — площадь, r — радиус вписанной окружности.
Если известны две стороны и угол между ними, вычислить периметр треугольника можно так:
P = √ b 2 + с 2 — 2 * b * с * cosα + (b + с), где b, с — известные стороны, α — угол между известными сторонами.
Если известна одна сторона в равностороннем треугольнике:
P = 3 * a, где a — длина стороны.
Все стороны в равносторонней фигуре равны.
Если известна боковая сторона и основание в равнобедренном треугольнике:
P = 2 * a + b, где a — боковая сторона, b — основание.
Боковые стороны в равнобедренной фигуре равны.
Если известна боковая сторона и высота в равнобедренном треугольнике:
P = 2 * (√ a 2 + h 2 ) + 2 * a, где a — боковая сторона, h — высота.
Высотой принято называть отрезок, который вышел из вершины и опустился на основание. В равнобедренной фигуре высота делит основание пополам.
Если известны катеты в прямоугольном треугольнике:
P = √ a 2 + b 2 + (a + b), где a, b — катеты.
Катет — одна из двух сторон, которые образуют прямой угол.
Если известны катет и гипотенуза в прямоугольном треугольнике:
P = √ c 2 — a 2 + (a + c), где a — любой катет, c — гипотенуза.
Гипотенуза — сторона, которая лежит напротив прямого угла.
Видео:Задача 6 №27624 ЕГЭ по математике. Урок 71Скачать

Скачать онлайн таблицу
У каждой геометрической фигуры много формул — запомнить все сразу бывает действительно сложно. В этом деле поможет регулярное решение задач и частый просмотр формул. Можно распечатать эту таблицу и использовать, как закладку в тетрадке или учебнике, и обращаться к ней по необходимости.
Видео:Окружность вписанная в треугольник и описанная около треугольника.Скачать

Периметр правильного треугольника

Средняя оценка: 4.6
Всего получено оценок: 106.
Средняя оценка: 4.6
Всего получено оценок: 106.
Правильный треугольник особенно выделяется на фоне других фигур. Любой параметр такого треугольника может быть определен из длины стороны. Особенной простотой отличается нахождение периметра.
Видео:Вариант 30, № 6. Нахождение периметра равностороннего треугольника, в который вписана окружностьСкачать

Определения
Для начала вспомним несколько определений, которые потребуются для того, чтобы решать задачи на нахождение периметра правильного треугольника:
- Правильным треугольником является треугольник, все стороны которого равны, а каждый из углов составляет 60 градусов.
- Правильный треугольник является частным случаем равнобедренного, поэтому любая высота правильного треугольника будет являться биссектрисой и медианой.
- Некоторые формулы для произвольного треугольника при применении к правильному треугольнику можно значительно упростить с помощью теоремы Пифагора.
Видео:Треугольник и окружность #shortsСкачать

Периметр треугольника
Что такое периметр? Это сумма длин всех сторон.
Формула периметра одинакова для любой фигуры. Это всегда сумма длин всех сторон.
Конкретно для правильного треугольника, нужно вспомнить, что все стороны этой фигуры равны между собой. Сторон у треугольника 3, а значит, формула периметра выглядит следующим образом:
Видео:№ 1089 - Геометрия 7-9 класс АтанасянСкачать

Пример
Сложную задачу на нахождение периметра правильного треугольника придумать нелегко. Поэтому решим интересную, но простую задачу на заданную тематику. В процессе решения рассмотрим применение теоремы Пифагора для решения задач с правильным треугольником.
Площадь правильного треугольника АВС равняется $9sqrt$
Любую характеристику правильного треугольника можно найти, если есть хотя бы одна из длин. Неважно, будет это сторона, площадь, периметр, медиана или биссектриса. Любой длины будет достаточно для решения задачи.
Вспомним формулу площади треугольника и упростим ее для правильного треугольника.
Площадь треугольника находится как половина произведения основания на высоту, проведенную к этому основанию.
В правильном треугольнике АВС проведем медиану АМ, которая совпадет с высотой и биссектрисой. Тогда треугольник АВМ будет прямоугольным. По теореме Пифагора найдем АМ.
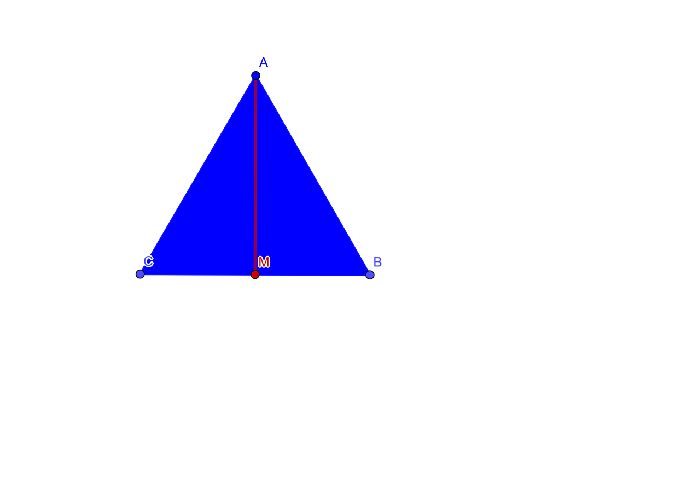
Подставим значение АМ в формулу площади:
Из этой формулы выразим значение стороны:
Теперь найти периметр не составит проблем.
Видео:Вписанная и описанная окружность - от bezbotvyСкачать

Что мы узнали?
Мы привели формулу периметра правильного треугольника. На примере показали, как можно найти площадь правильного треугольника через площадь. На том же примере показали примерный ход решения любой задачи на решение правильного треугольника.
📽️ Видео
Периметр правильного шестиугольника равен 72. Найдите диаметр описанной окружности.Скачать

9 класс, 24 урок, Формулы для вычисления площади правильного многоугольника, его стороныСкачать

№706. Найдите сторону равностороннего треугольника, если радиус описанной около него окружностиСкачать

Задача 6 №27910 ЕГЭ по математике. Урок 130Скачать

Формулы равностороннего треугольника #shortsСкачать

Задача 6 №27916 ЕГЭ по математике. Урок 133Скачать

Вписанные и описанные окружности. Вебинар | МатематикаСкачать

Геометрия 9 класс. Радиус описанной и вписанной окружности треугольника. Формулы радиуса.Скачать

Вписанный в окружность прямоугольный треугольник.Скачать

найти периметр квадрата, вписанного в окружность, если периметр треугольника = 6√3Скачать



