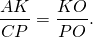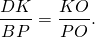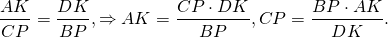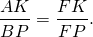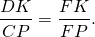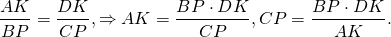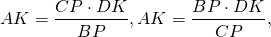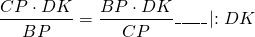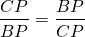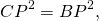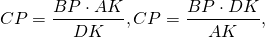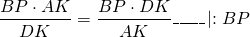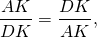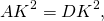Замечательное свойство трапеции доказательство через векторы (2 видео)

Замечательное свойство трапеции

Замечательное свойство трапеции

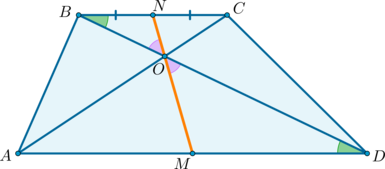
Точка пересечения диагоналей трапеции, точка пересечения продолжения боковых сторон трапеции и середины оснований трапеции лежат на одной прямой.

Существует несколько способов доказательства этого свойства. Надо доказать, что четыре данные точки лежат на одной прямой. Прямую можно провести через любые две точки. Выбирают две любые точки из четырёх, проводят через них прямую и доказывают, что две другие точки также лежат на этой прямой.

Сформулируем это свойство иначе:

Прямая, проходящая через точку пересечения диагоналей трапеции и точку пересечения продолжения её боковых сторон, делит основания трапеции пополам.

Дано:

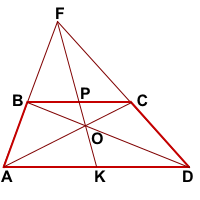
ABCD- трапеция, AD||BC,

Доказать: K- середина AD,

Рассмотрим треугольники AOK и COP.

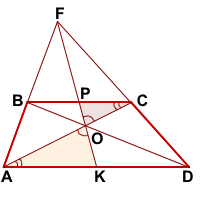
∠OAK=∠OCP (как внутренние накрест лежащие при AD||BC и секущей AC).

Значит, треугольники AOK и COP подобны (по двум углам).

Аналогично, треугольники DOK и BOP подобны и

Так как правые части этих равенств равны, то левые также равны:

Рассмотрим треугольники AFK и BFP.

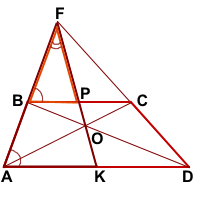
∠KAF=∠PBF (как соответственные при AD||BC и секущей AF).

Следовательно, треугольники AFK и BFP подобны (по двум углам).

Аналогично, треугольники DFK и CFP подобны и

Правые части равенств равны, приравниваем левые части:

а значит, CP=BP, то есть P — середина BC.

AK=DK, K — середина AD.

Что и требовалось доказать.

Докажем, что медиана, проведённая к стороне треугольника, делит пополам любой отрезок, параллельный этой стороне, с концами на двух других сторонах треугольника.
Докажем, что точка пересечения диагоналей трапеции и середина её меньшего основания лежат на прямой, проходящей через точку пересечения продолжения боковых сторон трапеции и середину большего основания

В нашем случае докажем, что точки O и P лежат на прямой FK.

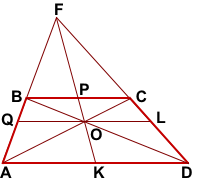
FK — медиана треугольника AFD.

Проведём через точку O пересечения диагоналей трапеции отрезок QL с концами на боковых сторонах трапеции.

BC||AD (как основания трапеции), QL||AD (по построению).

Так как медиана, проведённая к стороне треугольника, делит пополам любой отрезок, параллельный этой стороне, с концами на двух других сторонах треугольника, то точки P и O лежат прямой FK.

Поскольку медиана FK, проведённая к AD, делит пополам любой отрезок, параллельный AD, с концами на сторонах AF и DF, то среднюю линию трапеции она также делит пополам. Таким образом, замечательное свойство трапеции можно дополнить:

Точка пересечения диагоналей трапеции, точка пересечения продолжения боковых сторон трапеции, середины оснований трапеции и середина средней линии трапеции лежат на одной прямой.

Видео:Вектор. Сложение и вычитание. 9 класс | МатематикаСкачать

Замечательное свойство трапеции

Замечательное свойство трапеции. Точка пересечения диагоналей трапеции, точка пересечения продолжений ее боковых сторон и середины оснований лежат на одной линии.

Дана трапеция ABCD, , N — середина AD, M — середина BC, . Докажем, что точки M, N, O, P лежат на одной прямой.

Задача не так уж и проста, да и сама формулировка необычна: доказать, что четыре точки лежат на одной прямой. Как это сделать?

Во-первых, разобьем задачу на две более простых. Во-вторых – немного переформулируем.

1) Докажем, что середина основания AD лежит на прямой, соединяющей середину основания BC и точку пересечения диагоналей.

2) Докажем, что середина основания AD лежит на прямой, соединяющей середину основания BC и точку пересечения продолжений боковых сторон.

Начнем с пункта 1.

Пусть M — середина BC, O – точка пересечения диагоналей трапеции, .

Докажем, что N – середина AD.

по двум углам ( как вертикальные, как накрест лежащие при параллельных основаниях трапеции), тогда .

Аналогично, ( как вертикальные, как накрест лежащие при параллельных основаниях трапеция), отсюда .

Отсюда . Это значит, что N – середина AD.

Проведем PM – медиану треугольника BPC. Пусть прямые AD и PM пересекаются в точке N. Докажем, что N – середина AD

по двум углам (угол P – общий, как соответственные при параллельных основаниях трапеции), отсюда .

Получим: , значит, N – середина AD.

Таким образом, точки M,O,N,P лежат на одной прямой, что и требовалось доказать.

Видео:Замечательное свойство трапеции | ЕГЭ по математике 2020Скачать

Трапеция

Определения

Трапеция – это выпуклый четырехугольник, у которого две стороны параллельны, а две другие стороны не параллельны.

Параллельные стороны трапеции называются её основаниями, а две другие стороны – боковыми сторонами.

Высота трапеции – это перпендикуляр, опущенный из любой точки одного основания к другому основанию.

Теоремы: свойства трапеции

1) Сумма углов при боковой стороне равна (180^circ) .

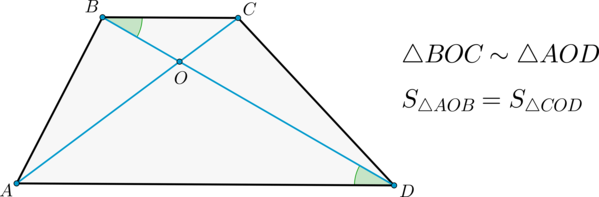
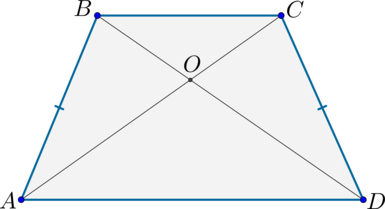
2) Диагонали делят трапецию на четыре треугольника, два из которых подобны, а два другие – равновелики.

Доказательство

1) Т.к. (ADparallel BC) , то углы (angle BAD) и (angle ABC) – односторонние при этих прямых и секущей (AB) , следовательно, (angle BAD +angle ABC=180^circ) .

2) Т.к. (ADparallel BC) и (BD) – секущая, то (angle DBC=angle BDA) как накрест лежащие.
Также (angle BOC=angle AOD) как вертикальные.
Следовательно, по двум углам (triangle BOC sim triangle AOD) .

Определение

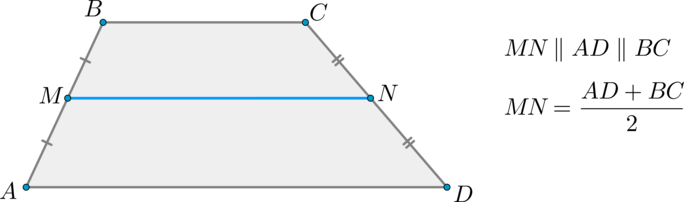
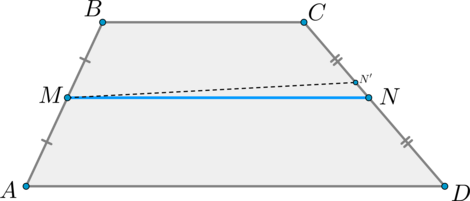
Средняя линия трапеции – отрезок, соединяющий середины боковых сторон.

Теорема

Средняя линия трапеции параллельна основаниям и равна их полусумме.

Доказательство*
С доказательством рекомендуется ознакомиться после изучения темы “Подобие треугольников”.

1) Докажем параллельность.

Проведем через точку (M) прямую (MN’parallel AD) ( (N’in CD) ). Тогда по теореме Фалеса (т.к. (MN’parallel ADparallel BC, AM=MB) ) точка (N’) — середина отрезка (CD) . Значит, точки (N) и (N’) совпадут.

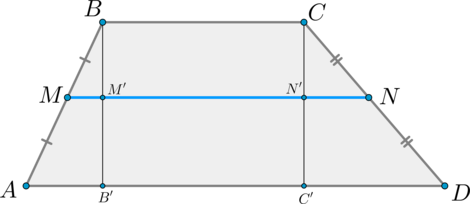
2) Докажем формулу.

Проведем (BB’perp AD, CC’perp AD) . Пусть (BB’cap MN=M’, CC’cap MN=N’) .

Тогда по теореме Фалеса (M’) и (N’) — середины отрезков (BB’) и (CC’) соответственно. Значит, (MM’) – средняя линия (triangle ABB’) , (NN’) — средняя линия (triangle DCC’) . Поэтому: [MM’=dfrac12 AB’, quad NN’=dfrac12 DC’]

Т.к. (MNparallel ADparallel BC) и (BB’, CC’perp AD) , то (B’M’N’C’) и (BM’N’C) – прямоугольники. По теореме Фалеса из (MNparallel AD) и (AM=MB) следует, что (B’M’=M’B) . Значит, (B’M’N’C’) и (BM’N’C) – равные прямоугольники, следовательно, (M’N’=B’C’=BC) .

[MN=MM’+M’N’+N’N=dfrac12 AB’+B’C’+dfrac12 C’D=] [=dfrac12 left(AB’+B’C’+BC+C’Dright)=dfrac12left(AD+BCright)]

Теорема: свойство произвольной трапеции

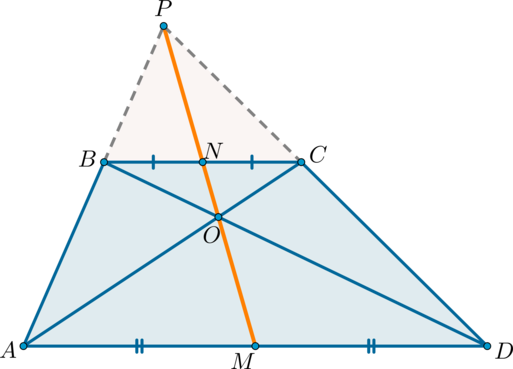
Середины оснований, точка пересечения диагоналей трапеции и точка пересечения продолжений боковых сторон лежат на одной прямой.

1) Докажем, что точки (P) , (N) и (M) лежат на одной прямой.

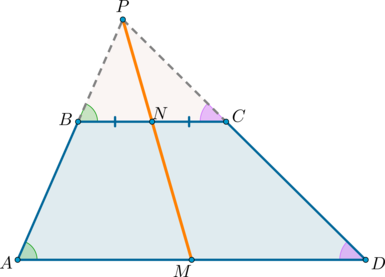
Проведем прямую (PN) ( (P) – точка пересечения продолжений боковых сторон, (N) – середина (BC) ). Пусть она пересечет сторону (AD) в точке (M) . Докажем, что (M) – середина (AD) .

Рассмотрим (triangle BPN) и (triangle APM) . Они подобны по двум углам ( (angle APM) – общий, (angle PAM=angle PBN) как соответственные при (ADparallel BC) и (AB) секущей). Значит: [dfrac=dfrac]

Рассмотрим (triangle CPN) и (triangle DPM) . Они подобны по двум углам ( (angle DPM) – общий, (angle PDM=angle PCN) как соответственные при (ADparallel BC) и (CD) секущей). Значит: [dfrac=dfrac]

Отсюда (dfrac=dfrac) . Но (BN=NC) , следовательно, (AM=DM) .

2) Докажем, что точки (N, O, M) лежат на одной прямой.

Пусть (N) – середина (BC) , (O) – точка пересечения диагоналей. Проведем прямую (NO) , она пересечет сторону (AD) в точке (M) . Докажем, что (M) – середина (AD) .

(triangle BNOsim triangle DMO) по двум углам ( (angle OBN=angle ODM) как накрест лежащие при (BCparallel AD) и (BD) секущей; (angle BON=angle DOM) как вертикальные). Значит: [dfrac=dfrac]

Аналогично (triangle CONsim triangle AOM) . Значит: [dfrac=dfrac]

Отсюда (dfrac=dfrac) . Но (BN=CN) , следовательно, (AM=MD) .

Определения

Трапеция называется прямоугольной, если один из ее углов – прямой.

Трапеция называется равнобедренной, если ее боковые стороны равны.

Теоремы: свойства равнобедренной трапеции

1) У равнобедренной трапеции углы при основании равны.

2) Диагонали равнобедренной трапеции равны.

3) Два треугольника, образованные диагоналями и основанием, являются равнобедренными.

Доказательство

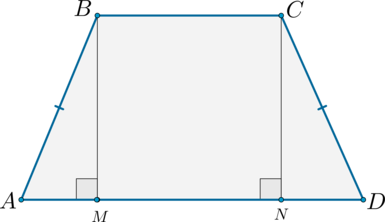
1) Рассмотрим равнобедренную трапецию (ABCD) .

Из вершин (B) и (C) опустим на сторону (AD) перпендикуляры (BM) и (CN) соответственно. Так как (BMperp AD) и (CNperp AD) , то (BMparallel CN) ; (ADparallel BC) , тогда (MBCN) – параллелограмм, следовательно, (BM = CN) .

Рассмотрим прямоугольные треугольники (ABM) и (CDN) . Так как у них равны гипотенузы и катет (BM) равен катету (CN) , то эти треугольники равны, следовательно, (angle DAB = angle CDA) .

Т.к. (AB=CD, angle A=angle D, AD) – общая, то по первому признаку (triangle ABD=triangle ACD) . Следовательно, (AC=BD) .

3) Т.к. (triangle ABD=triangle ACD) , то (angle BDA=angle CAD) . Следовательно, треугольник (triangle AOD) – равнобедренный. Аналогично доказывается, что и (triangle BOC) – равнобедренный.

Теоремы: признаки равнобедренной трапеции

1) Если у трапеции углы при основании равны, то она равнобедренная.

2) Если у трапеции диагонали равны, то она равнобедренная.

Доказательство

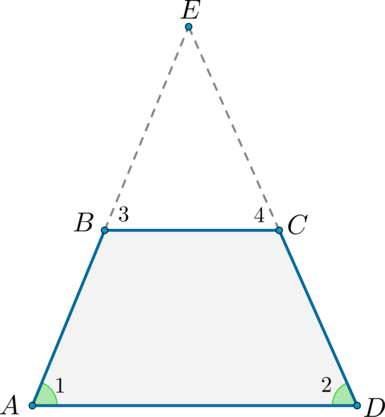
Рассмотрим трапецию (ABCD) , такую что (angle A = angle D) .

Достроим трапецию до треугольника (AED) как показано на рисунке. Так как (angle 1 = angle 2) , то треугольник (AED) равнобедренный и (AE = ED) . Углы (1) и (3) равны как соответственные при параллельных прямых (AD) и (BC) и секущей (AB) . Аналогично равны углы (2) и (4) , но (angle 1 = angle 2) , тогда (angle 3 = angle 1 = angle 2 = angle 4) , следовательно, треугольник (BEC) тоже равнобедренный и (BE = EC) .

В итоге (AB = AE — BE = DE — CE = CD) , то есть (AB = CD) , что и требовалось доказать.

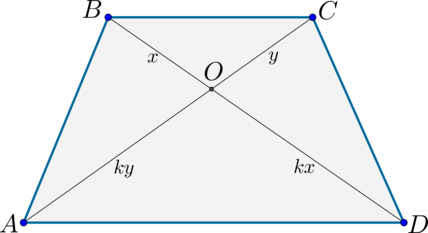
2) Пусть (AC=BD) . Т.к. (triangle AODsim triangle BOC) , то обозначим их коэффициент подобия за (k) . Тогда если (BO=x) , то (OD=kx) . Аналогично (CO=y Rightarrow AO=ky) .