Роль параллельных прямых в жизни человека (2 видео)

Параллельные прямые

Вы будете перенаправлены на Автор24

Содержание

Понятие параллельных прямых
Готовые работы на аналогичную тему
Историческая справка
Параллельные прямые в жизни
Параллельные прямые в архитектуре
Параллельные прямые в математике и в жизни
Проект по теме: Параллельные прямые в жизни
«Управление общеобразовательной организацией: новые тенденции и современные технологии»
🔥 Видео

Видео:Математика это не ИсламСкачать

Понятие параллельных прямых

Параллельные прямые – прямые, которые лежат в одной плоскости, не совпадают и не имеют общих точек.

Если у прямых есть общая точка, тогда они пересекаются.

Если все точки прямых совпадают, то имеем по сути одну прямую.

Если прямые лежат в разных плоскостях, то условий их параллельности несколько больше.

При рассмотрении прямых на одной плоскости можно дать следующее определение:

Две прямые на плоскости называют параллельными, если они не пересекаются.

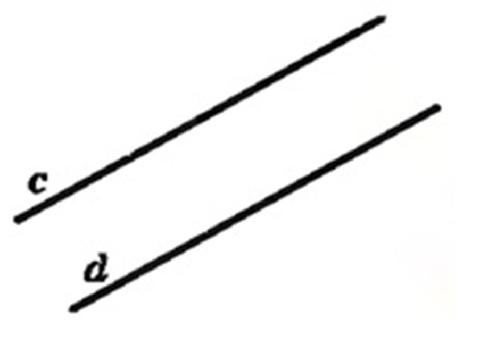
В математике параллельные прямые принято обозначать с помощью знака параллельности « $parallel$ ». Например, тот факт, что прямая $c$ параллельна прямой $d$ обозначается следующим образом:

Зачастую рассматривается понятие параллельных отрезков.

Два отрезка называют параллельными, если они лежат на параллельных прямых.

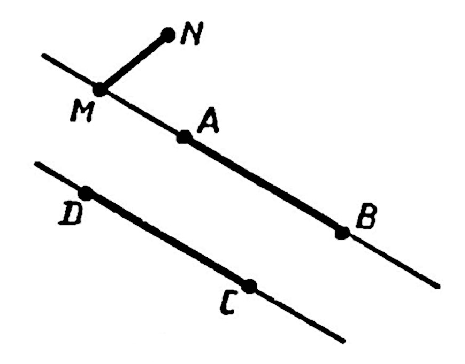
Например, на рисунке параллельными являются отрезки $AB$ и $CD$, т.к. они принадлежат параллельным прямым:

Вместе с тем, отрезки $MN$ и $AB$ или $МN$ и $CD$ параллельными не являются. Этот факт можно записать с помощью символов следующим образом:

Готовые работы на аналогичную тему

$MN ∦ AB$ и $MN ∦ CD$.

Аналогичным образом определяется параллельность прямой и отрезка, прямой и луча, отрезка и луча или двух лучей.

Видео:Параллельность прямых. 10 класс.Скачать

Историческая справка

С греческого языка понятие «параллелос» переводится «рядом идущий» или «проведенный друг возле друга». Этот термин использовался в древней школе Пифагора еще до того, как параллельные прямые получили свое определение. Согласно историческим фактам Евклидом в $III$ в. до н.э. в его трудах все же был раскрыт смысл понятия параллельных прямых.

В древности знак для обозначения параллельных прямых имел отличный вид того, что мы используем в современной математике. Например, древнегреческим математиком Паппом в $III$ в. н.э. параллельность обозначалась с помощью знака равенства. Т.е. тот факт, что прямая $l$ параллельна прямой $m$ ранее обозначался «$l=m$». Позднее для обозначения параллельности прямых стали использовать привычный нам знак «$parallel$, а знак равенства стали использовать для обозначения равенства чисел и выражений.

Видео:Параллельные прямые | Математика | TutorOnlineСкачать

Параллельные прямые в жизни

Электрические провода, которые расположены вдоль улиц и дорог, также проходят параллельно. Рельсы линий метро и железных дорог располагаются параллельно.

Кроме быта параллельные линии можно встретить в живописи, в архитектуре, при строительстве зданий.

Видео:Геометрия 7 класс (Урок№21 - Свойства параллельных прямых.)Скачать

Параллельные прямые в архитектуре

В живописи параллельные линии изображают сводящимися в одну линию или близкими к тому. Такой прием называется перспективой, которая следует из иллюзии зрения. Если долго смотреть вдаль, то параллельные прямые будут похожи на две сходящиеся линии.

Видео:Геометрия 7 класс (Урок№18 - Параллельные прямые.)Скачать

Параллельные прямые в математике и в жизни

1.Понятие о параллельных прямых

-в массовом сознании,

2. Модели Лобачевского, Клейна, Пуанкаре.

3. Открытие в математике – параллельные миры существуют!

4. Большой адронный коллайдер откроет параллельные миры.

5. Параллельные миры в литературе 18 века.

Большинство людей убеждено, что в математике все понятия определяются и все утверждения доказываются. Но ведь каждое понятие определяют через другие понятия, а каждое утверждение доказывают, опираясь на другие утверждения. Самое интересное — что же знают и думают люди об аксиоме параллельных прямых. И все ли здесь на самом деле так просто, однозначно и очевидно, как кажется на первый взгляд?!

Что такое параллельные прямые, знают практически все. Практически все слышали про аксиому о параллельных прямых, ведь её проходят в школе. Абсолютное большинство опрошенных нами взрослых и подростков отвечали так: аксиома о параллельных состоит в том, что параллельные прямые не пересекаются. Именно такая формулировка аксиомы о параллельных бытует в массовом сознании. Получив указанный выше ответ, следует немедленно задать следующий вопрос: а что такое параллельные прямые? Скорее всего, вам ответят, что параллельными называются такие прямые, которые не пересекаются. Многие сразу же осознают: тут что-то не так, ибо не может же аксиома заключаться в том, что непересекающиеся прямые не пересекаются. Многих из тех, кто не поймёт этого сразу сам, удастся в этом убедить. Останется незначительное меньшинство, считающее, что аксиома о непересекаемости непересекающихся прямых имеет право на существование.

В традиционной Евклидовой геометрии аксиома на самом деле звучит так: «через точку, не лежащую на прямой, можно провести только одну прямую параллельную данной». А вот определение параллельных прямых: «Две прямые в пространстве называются параллельными, если они лежат в одной плоскости и не пересекаются». А вот, к примеру, прямые, которые не пересекаются, но лежат в разных плоскостях, называются скрещивающимися. Но также существует много теорий, которые не сходятся и даже опровергают Евклидову (элементарную) геометрию. Одна из таких: «Геометрия Лобачевского».

7 февраля 1826 Лобачевский представил для напечатания в Записках физико-математического отделения сочинение: «Сжатое изложение начал геометрии со строгим доказательством теоремы о параллельных». Но издание не осуществилось. Рукопись и отзывы не сохранились, однако само сочинение было включено Лобачевским в его труд «О началах геометрии» (1829—1830), напечатанный в журнале «Казанский вестник». Это сочинение стало первой в мировой литературе серьёзной публикацией по неевклидовой геометрии, или геометрии Лобачевского.

Лобачевский считает аксиому параллельности Евклида произвольным ограничением. С его точки зрения, это требование слишком жёсткое, ограничивающее возможности теории, описывающей свойства пространства. В качестве альтернативы предлагает другую аксиому: на плоскости через точку, не лежащую на данной прямой, проходит более чем одна прямая, не пересекающая данную.

Вот модель этого дела:

Доказательством непротиворечивости какой-либо геометрии является построение модели. Одной из первых моделей, в которой «работает» геометрия Лобачевского, является круг. Неевклидовыми точками будут считаться те, которые расположены внутри него (заметим, в аксиоматики Лобачевского, аксиома параллельности заменена его личной аксиомой, остальные аксиомы Евклидовой геометрии остались). Точки, лежащие на окружности, исключаем из рассмотрения. Прямыми будем считать хорды данной окружности. Из точки A проведем хорду AB. Концы данной хорды лежат на окружности, следовательно, мы принять их не можем, все же точки, лежащие внутри круга и принадлежащие хорде AB являются неевклидовыми, и мы их можем принять во внимание, но какое бы малое расстояние мы не брали приближаясь к точке A, все равно будет существовать еще более маленькое, еще более близкое к точке A. Отсюда можно сделать вывод: хорда AB не имеет четко определенного начала и конца, следовательно, AB – прямая.
Пусть даны неевклидова прямая AB и точка C вне ее. Бесконечное множество прямых, проходящих через точку C, не пересекают хорду-прямую AB.

Но Лобачевский далеко не единственный разрабатывал подобные теории. Существуют модели, которые были как до, так и после открытия Лобачевского.

Над ними работали Э. Бельтрам (1868), Ф. Клейн (1871), А. Пуанкаре (1883), а также Фридрих Гаусс.

Вот представлены модели некоторых из них:

Модель Клейна

Плоскостью служит внутренность круга, прямой — хорда круга без концов, а точкой — точка внутри круга. «Движением» назовём любое преобразование круга в самого себя, которое переводит хорды в хорды. Соответственно, равными называются фигуры внутри круга, переводящиеся одна в другую такими преобразованиями. Тогда оказывается, что любой геометрический факт, описанный на таком языке, представляет теорему или аксиому геометрии Лобачевского. Иными словами, всякое утверждение геометрии Лобачевского на плоскости есть не что иное, как утверждение евклидовой геометрии, относящееся к фигурам внутри круга, лишь пересказанное в указанных терминах.

Модель Пуанкаре.

За плоскость Лобачевского принимается внутренность круга, прямыми считаются дуги окружностей, перпендикулярных окружности данного круга, и его диаметры, движениями — преобразования, получаемые комбинациями инверсий относительно окружностей, дуги которых служат прямыми.

Модель Пуанкаре замечательна тем, что в ней углы изображаются обычными углами.

Но напоминаю, что о параллельных прямых мы не только на геометрии слышим. Они встречаются в жизни везде, куда не посмотри! Параллельные грядки и ряды деревьев в посадках, рельсы и шпалы на железной дороге, параллельные эскалаторы в торговых центрах, поднимающие и опускающие нас с этажа на этаж, беговые дорожки параллельные брусья на стадионе, и даже цветы, растущие рядом, тянутся к солнцу параллельно…

Но вот еще интересная вещь: даже миры могут быть параллельными!

Команда ученых во главе с Дэвидом Deutsch Оксфорде сделали открытие в области математики. Параллельные миры действительно существуют.

Сама теория таких миров появилась еще в 1950 в США (автор — Хью Эверетт) и объяснила тайны квантовой механики, вызывавшие споры ученых. В Эвереттовской «многомирной» Вселенной каждое новое событие возможно и вызывает разделение Вселенной. Число возможных альтернативных исходов равно числу миров.

К примеру, водитель машины видит выскочившего на дорогу пешехода. В одной реальности он, избегая наезда, гибнет сам, в другой попадает в больницу и остается живым, в третьей гибнет пешеход. Число альтернативных сценариев бесконечно.

Теория была признана фантастической и забыта. Но неожиданно в Оксфорде в ходе математического исследования обнаружили, что Эверетт был на верном пути.

Согласно квантовой механике, до эксперимента про то, что внутри атома, нельзя сказать, что оно реально существует. До замеров частицы занимают неясную «суперпозицию», в которой они могут иметь одновременно верхний и нижний спин, или появляться в разных местах в одно и то же время. Наблюдение проводят для «проявления» конкретного состояния реальности, ведь и подброшенная монета приходит только в 1 положение «орел» или «решка», как только ее поймают.

Главный вывод из открытия состоит в следующем. Кустоподобные ветвящиеся структуры, возникающие при расщеплении Вселенной на параллельные версии ее самой, объясняют вероятностный характер результатов в квантовой механике. То есть неизбежно мы живем лишь в одном из множества параллельных миров, а не в единственном.

Физики Европейской организации ядерных исследований (ЦЕРН) приближаются к главному открытию XXI века, пытаясь доказать, что параллельные вселенные – это не выдумки фантастов, а реальный факт. Именно в 2013 году Большой адронный коллайдер будет выведен на рабочий максимум. Главным открытием этого момента станет создание модели рождения нашей Вселенной, а другие миры, в том числе и путешествия во времени, пока кажущихся выдумкой фантастов, по мнению ученых, приложатся. В октябрьском сообщении пресс-службы ЦЕРН поясняется, что до сих пор ученые не смогли найти доказательства существования параллельных вселенных лишь потому, что другие миры «спрятаны» в измерениях, куда не проникает свет. Однако воссоздание рождения Вселенной должно помочь исправить эту проблему. Несколько лет назад стало известно о сенсационной работе оксфордского теоретика Дэвида Дойча. Большой поклонник таланта Эверетта израильский физик Дойч создал математическую модель, согласно которой параллельные миры реальны. В этих вселенных не работают законы классической квантовой теории. При этом ученый верит и в возможность путешествий во времени. Пока же физики, работающие с коллайдером, опережают собственные графики.

Концепция существования иных миров, отличающихся от нашего, возникла в литературе 18 века. Пример — «Кандид» Вольтера, где один из персонажей, Панглос, заявляет ставшую крылатой фразу: «Все к лучшему в этом лучшем из миров».

В повести братьев Стругацких «Понедельник начинается в субботу» описаны путешествия персонажей в разные варианты описываемого фантастами будущего.

Также интересно описывает теорию параллельных миров Алексей Фомичев в своей серии книг «Пусть бог не вмешивается».

Список использованных источников

1. Геометрия 7-9, учебник для общеобразовательных учреждений,

Л.С. Атанасян, В.Ф. Бутузов, С.Б. Кадомцев и др., Москва, Просвещение,

2. Геометрия 10-11, учебник для общеобразовательных учреждений,

Л.С. Атанасян, В.Ф. Бутузов, С.Б. Кадомцев и др., Москва, Просвещение,

3. Глейзер Г. И. История математики в школе: 7-8 и 9-10 кл. Пособие для

Видео:24. Определение параллельных прямыхСкачать

Проект по теме: Параллельные прямые в жизни

Видео:Построение параллельных прямыхСкачать

«Управление общеобразовательной организацией:
новые тенденции и современные технологии»

Свидетельство и скидка на обучение каждому участнику

I . Теоретическая часть

1.1. Определение параллельных прямых . . 4

1.2. Параллельные прямые в жизни . 4

1.3. Иллюзии параллельных прямых . 5

1.4.Способы построения параллельных прямых . 6

1.5.Профессиональные способы построения параллельных прямых …………7

1.6.Применение параллельных прямых в геометрии …………………………..7

II . Практическая часть

2.1. Анкетирование учащихся. 9

2.2. Изготовление проектного продукта…………… . 9

Список литературы . 11

Каждый современный ученик должен быть всесторонне развитым, поэтому ему необходимо владеть не только математическими знаниями, но и знать историю математики . Школьная программа , к сожалению, не предусматривает изучение вопроса «История параллельных прямых», а способы построения параллельных прямых изучаются не в полном объёме. Исходя из этого, я решила расширить свои знания в области математики, а именно: изучить историю параллельных прямых, показать их значимость и закрепить умения строить параллельные прямые на линованной и нелинованной бумаге. Поэтому выбранная мной тема исследования актуальна.

Гипотеза: Без параллельных прямых невозможна наша жизнь.

Цель моего проекта: Показать необходимость и значимость параллельных прямых.

1. Собрать материал по теме, изучив литературу и Интернет-источники.

2. Изучить определения, способы построения и применение параллельных прямых в жизни .

3. Провести анкетирование обучающихся школы.

4. Составить буклет “ Параллельные прямые в жизни”.

1.1. Определение параллельных прямых

В домашних справочных и энциклопедических изданиях я нашла несколько определений понятиям «параллель» и «параллельные прямые». Например, в самом популярном толковом словаре русского языка С. И. Ожегова и Н. Ю. Шведовой параллелью в математике называется «Прямая, не пересекающаяся другой прямой, лежащей с ней в одной плоскости».

А из занимательного толкового словаря В. И. Даля – “ПАРАЛЛЕЛЬ” ж. — параллельная линия, равна во всех точках от другой отстоящая и потому никогда не могущая с нею встретиться.

В евклидовой геометрии параллельными прямыми называются прямые, которые лежат в одной плоскости и не пересекаются. В другом варианте определения, совпадающие прямые также считаются параллельными (Приложение 4, рис. 27)

Через любую точку, не лежащую на прямой, можно провести прямую, параллельную данной, и притом только одну. Последняя часть этого утверждения — знаменитый пятый постулат Евклида . Отказ от пятого постулата ведёт к геометрии Лобачевского (Приложение 8).

В геометрии Лобачевского вместо неё принимается следующая аксиома: Через точку, не лежащую на данной прямой, проходят, по крайней мере, две прямые, лежащие с данной прямой в одной плоскости и не пересекающие её (Приложение 4, рис. 25; рис. 26).

Согласно историческим фактам Евклидом в III в. До н.э. в его трудах все же был раскрыт смысл понятия параллельных прямых (Приложение 4, рис. 1).

В древности знак для обозначения параллельных прямых имел отличный вид того, что мы используем в современной математике. Например, древнегреческим математиком Паппом в III в. Н.э. параллельность обозначалась с помощью знака равенства. Т.е. тот факт, что прямая l параллельна прямой m ранее обозначался «l=m». Позднее для обозначения параллельности прямых стали использовать привычный нам знак « ∥» , а знак равенства стали использовать для обозначения равенства чисел и выражений.

1.2. Параллельные прямые в жизни

Зачастую мы не замечаем, что в обычной жизни нас окружает огромное число параллельных прямых. Например, в нотной тетради и сборнике песен с нотами нотный стан выполнен с помощью параллельных линий (Приложение 4, рис. 2). Также параллельные линии встречаются и в музыкальных инструментах (например, струны арфы, гитары, клавиши фортепиано и т.п.) (Приложение 4, рис. 3). Электрические провода, которые расположены вдоль улиц и дорог, также проходят параллельно (Приложение 4, рис. 4). Рельсы линий метро и железных дорог располагаются параллельно. Кроме быта параллельные линии можно встретить в живописи, в архитектуре, при строительстве зданий (Приложение 4, рис. 5; рис. 6 ; рис. 7).

На представленных изображениях архитектурные сооружения содержат параллельные прямые. Использование параллельности прямых в строительстве помогает увеличить срок службы таких сооружений и придает им необычайную красоту, привлекательность и величие. Линии электропередач также умышленно проводятся параллельно, чтобы избежать их пересечения или соприкосновения, что привело бы к замыканию, перебоям и отсутствию электричества. Чтобы поезд мог беспрепятственно перемещаться, рельсы также выполнены параллельными линиями. В живописи параллельные линии изображают сводящимися в одну линию или близкими к тому. Такой прием называется перспективой, которая следует из-за иллюзии зрения. Если долго смотреть вдаль, то параллельные прямые будут похожи на две сходящиеся линии.

1.3.Иллюзии параллельных прямых

Слово «иллюзия» происходит от латинского illusere – обманывать.

Зрительная иллюзия – ошибка в зрительном восприятии, искажение пространственных соотношений признаков воспринимаемых объектов, ошибка в оценке и сравнении между собой длин отрезков, величин углов, расстояний между предметами, в восприятии формы предметов, совершаемые наблюдателем при определенных условиях.

Начало изучению зрительных иллюзий положило обнаружение немецким астрофизиком Ф. Цёлльнером (1860 г.) в рисунке купленной ткани эффекта визуального схождения и расхождения вертикальных параллельных линий при пересечении их короткими косыми линиями. Эта иллюзия наиболее сильно проявляется, когда пересекающееся линии образуют угол, равный 45° (Приложение 3, рис. 8).

На уроках геометрии, приступая к решению задачи, мы, как правило, первым делом строим чертёж, опираясь на свое зрительное восприятие. Но такой подход к решению задачи часто приводит к ошибочным выводам, а значит к неверному решению. Мы привыкли доверять собственному зрению, однако оно нередко обманывает нас, показывая то, чего в действительности не существует. В такие моменты мы сталкиваемся со зрительными иллюзиями — ошибками зрительного восприятия (Приложение 3, рис. 9; рис. 10; рис. 11).

В настоящее время люди не только поражаются обманам зрения и забавляются зрительными иллюзиями, но и сознательно используют их в своей практической деятельности. Иллюзии применяются в архитектуре, изобразительном, цирковом искусстве, кинематографии и даже в военном деле (Приложение 3, рис. 12; рис. 13; рис. 14).

Но с другой стороны мы столкнулись со странным явлением: устремляя взгляд далеко в бесконечность, можно увидеть пересечение параллельных прямых!

В чем же дело? Чтобы ответить на этот вопрос обратимся к великим ученым.

Но сначала я обратилась к учащимся 7 Б класса. С ними провела эксперимент «Иллюзии зрения». Учащимся задали вопрос: везде ли на картинках параллельные прямые? Результаты опроса таковы: участвовали 20 человек из них: 7 – 35% считают параллельно, 13 -65% нет (Приложение 3).

Вывод: в геометрии истинность каждого утверждения необходимо доказывать, нельзя полагаться только на наблюдения.

Положительный момент: благодаря зрительным искажениям существует живопись.

1.4. Способы построения двух параллельных прямых

Изучив теоретические сведения, касающиеся параллельных прямых, возникла необходимость к изучению практических способов геометрических построений параллельных прямых на плоскости. Рассмотрим некоторые из них (Приложение 7):