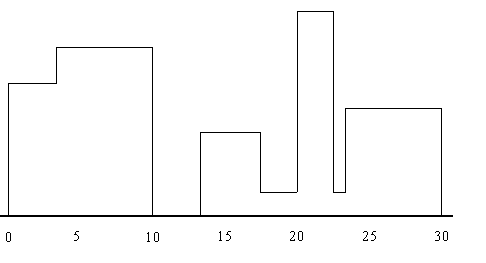Расчёт площади многоугольника — это одна из наиболее распространенных задач вычислительной геометрии. Варианты решения этой задачи зависят от способа условий задачи. Так, если многоугольник задан в виде упорядоченного набора координат его вершин, то задача о нахождении площади многоугольника формулируется следующим образом: площадь многоугольника — замкнутой ломаной без самопересечений, заданной своими вершинами в порядке обхода, вычисляется по формуле:
где X0,Y0 = Xn+1,Yn+1 (координаты последней точки совпадают с первой). Таким образом, реализация алгоритма вычисления площади многоугольника в C# может базироваться как на использовании «простых» типов данных, например, с использованием массивов, так и на использовании списков (List, LinkedList). Сегодня рассмотрим вариант реализации алгоритма определения площади многоугольника с использованием двусвязного списка.
- Задача и условия
- Алгоритм вычисления площади многоугольника
- Реализация алгоритма вычисления площади многоугольника в C#
- Программа вычисления площади многоугольника в C#
- Результаты работы программы
- Итого
- Вычислительная геометрия
- Заданы координаты вершин четырехугольника вывести их в порядке обхода по часовой стрелке
- 📽️ Видео
Видео:Нахождение длины вектора через координаты. Практическая часть. 9 класс.Скачать

Задача и условия
Многоугольник задан в виде замкнутой ломаной линии без самопересечений. Координаты вершин (X, Y) многоугольника заданы в порядке в порядке их обхода (по часовой или против часовой стрелки). Необходимо определить площадь многоугольника.
Видео:№402. Даны координаты четырех вершин куба ABCDA1B1C1D1: А (0; 0; 0), В (0; 0; 1), D (0; 1; 0)Скачать

Алгоритм вычисления площади многоугольника
Используя навыки работы с двусвязными списками, алгоритм расчёта площади многоугольника можно представить следующим образом:
- N-угольник задается списком из N+1 вершин где N+1 вершина совпадает с первой ;
- Используя формулу, представленную выше, в цикле рассчитываем площадь многоугольника;
- Выводим результат расчёта
Видео:№933. Найдите координаты вершины D параллелограмма ABCD, если А (0; 0), B (5; 0), С (12; -3.).Скачать

Реализация алгоритма вычисления площади многоугольника в C#
Вершину многоугольника можно описать в виде такого класса:
или использовать готовый класс PointF из пространства имен System.Drawing .
Все вершины будем хранить в списке:
Цикл в котором рассчитывается площадь:
Видео:№973. Даны координаты вершин треугольника ABC: А (4; 6), В (-4; 0), С (-1; -4). Напишите уравнениеСкачать

Программа вычисления площади многоугольника в C#
Ниже представлен код программы, реализующей расчёт площади многоугольника в C#:
Помимо непосредственно расчёта площади, в программе также реализована проверка ввода пользователем координат — любой многоугольник должен состоять минимум из трех вершин. Последняя (замыкающая вершина с индексом N+1 ) добавляется программой автоматически после набора пользователем команды «Calc»:
Видео:Геометрия на С++. Поиск осей симметрии выпуклого четырехугольникаСкачать

Результаты работы программы
Ниже представлен скриншот работы программы по расчёту площади многоугольника в C#
Видео:Найдите площадь треугольника АВС, если А(5;2;6), В(1;2;0), С(3;0;3)Скачать

Итого
Сегодня мы рассмотрели пример реализации алгоритма расчёта площади многоугольника заданного в виде упорядоченного набора координат его вершин. Для реализации алгоритма в C# использован двусвязный список.
Видео:Даны вершины пирамиды A, B, C, D. Найдите объём пирамиды и высоту, опущенную на грань ACDСкачать

Вычислительная геометрия
11. Вычислительная геометрия
Вычислительная геометрия – один из разделов информатики. Существует большое количество научных и прикладных задач, связанных с вычислительной геометрией.
Рассмотрим сначала типы данных, применяемых для вычислений. Точка на плоскости описывается парой вещественных чисел. При использовании вещественного типа операции сравнения лучше всего оформить специальными функциями, то есть сравнения вида A=B, где A и B вещественные числа, использовать не стоит. Приведем пример [4].
Пусть для хранения вещественного типа используются два десятичных разряда для порядка и шесть разрядов для хранения мантиссы. Есть два числа: A=0.34567´104 и B=0.98765´10-4. При сложении и вычитании происходит выравнивание порядков, сложение (вычитание) мантисс и нормализация результата. После выравнивания порядков получим B=0.0000000098765´104, а после сложения мантисс и будет результат:
A+B = 0. 3456700098765
При шести десятичных разрядах мантиссы после округления окажется, что A+B=A при B>0! В реальных системах тоже есть подобные ограничения на разрядность представления вещественного типа данных. Например, для типа Real в ПАСКАЛе мантиссе отводится 11-12 цифр.
Операцию проверки равенства вещественных чисел можно реализовать следующей функцией:
Function IsEqual(A, B: real): boolean;
IsEqual:=Abs(A-B) B) or Abs(A-B) 0 then WhatZnak:=1
else if V S) or ((Abs(C-S) E)) then
Function Perim(Var H:ArrPara; L:integer): real;
Function Squ(Var H:ArrPara; L:integer): real;
ReadLn(Fin, A[i].X, A[i].Y);
Задачи для самостоятельного решения
11.1. Треугольник и точка (5)
В декартовой системе координат на плоскости заданы координаты вершин треугольника и еще одной точки. Определить, принадлежит ли эта точка треугольнику.
Ввод из файла INPUT. TXT. В четырех строках находятся пары чисел — координаты точек. Числа в первых трех строках — это координаты вершин треугольника, в четвертой строке — координаты тестируемой точки.
Вывод в файл OUTPUT. TXT. Вывести In, если точка находится внутри треугольника, или Out — если снаружи.
Ограничения: координаты вершин — целые числа, для любой точки выполняются следующие условия: -109 ≤ x, y ≤ 109, время 1 с.
0 0 0 0 0 0 0 0
100 0 100 0 100 0 100 0
0 100 0 100 0 100 0 100
100 100 10 10 50 50 0 0
11.2. Левые повороты (4)
Маршрут движения автомобиля задан в виде координат вершин ломаной. Необходимо определить количество левых поворотов (смежные участки ломаной не лежат на одной прямой). Автомобиль начинает движение из первой вершины ломаной.
Ввод. Первая строка состоит из одного числа N (3 £ N £ 1000), количества звеньев ломаной. В последующих строках — пары натуральных чисел (Xi, Yi), координаты вершин ломаной (-104 £ Xi, Yi £ 104).
Вывод. Выходной файл содержит одно число — количество левых поворотов.
11.3. Даешь квадрат (5)
Ломаная без самопересечений и самокасаний разделяет четырехугольник на две части, которые не лежат одна внутри другой. Каждая часть представляет собой многоугольник и задается отдельно путем перечисления координат вершин. Определить, является ли исходный четырехугольник квадратом.
Ввод из файла INPUT. TXT. В первой строке находится число M, задающее количество вершин первого многоугольника. Следующие M строк содержат пары целых чисел — координаты точек (Xi, Yi). Если соединить точки в данном порядке, а также первую и последнюю точки, то получится первый многоугольник. Далее аналогично указываются число N – количество вершин второго многоугольника и N строк с координатами его вершин. Таким образом, тест занимает M + N + 2 строк. Начальная вершина и направление обхода вершин каждого многоугольника могут быть произвольными.
Вывод в файл OUTPUT. TXT. Выводится единственная строка со значением Yes или No – является четырехугольник квадратом или нет.
Ограничения: 3 ≤ M, N ≤ 1000; -100 ≤ Xi, Yi ≤ 100; время 1 с.
Вывод 1 Вывод 2
Жил-был жадный Король. Он приказал своему главному Архитектору построить стену вокруг его замка. Король был таким жадным, что не послушал предложение Архитектора построить красивую кирпичную стену совершенной формы с изящными высокими башнями. Вместо этого он приказал построить стену вокруг всего замка, используя минимальное количество камня, но потребовал, чтобы стена не подходила к замку ближе некоторого расстояния. Если Король узнает, что Архитектор использовал больше ресурсов для постройки стены, чем было абсолютно необходимо для удовлетворения требований, Архитектор лишится головы. Более того, Архитектор должен представить проект стены, где указано точное количество ресурсов.
Ваша задача — помочь Архитектору сохранить голову, написав программу, определяющую минимальную длину стены, которую можно построить вокруг замка, удовлетворив требования Короля.
Задача слегка упрощается тем, что замок Короля представляет собой многоугольник и расположен на плоской поверхности. Архитектор уже сопоставил замку прямоугольную декартову систему координат и точно определил координаты каждого угла замка в футах.
Ввод из файла INPUT. TXT. Первая строка содержит два целых числа N и L, разделённых пробелом: N — число углов в замке Короля, а L — минимальное число футов, на которое Король разрешил приблизить стену к замку.
Следующие N строк описывают координаты углов замка в порядке обхода по часовой стрелке. Каждая строка содержит два целых числа xi и yi, разделённых пробелом и представляющих собой координаты i-го угла в футах. Все углы имеют различные координаты, и стены замка не пересекаются иначе как в углах.
Ограничения: 3 ≤ N ≤ 1000, 1 ≤ L ≤ 1000, -10000 ≤ xi, yi ≤ 10000, время 2 с.
Вывод в файл OUTPUT. TXT. Выводится единственное число — минимальная длина стены в футах, которая может быть построена вокруг замка согласно требованиям Короля с точностью до фута.
Кладоискатели обнаружили люк в подземелье с сокровищами, закрытый неподъемной квадратной чугунной плитой. К счастью, плита имеет сквозную трещину, разделяющую ее на две части, которые не лежат полностью одна внутри другой. Трещина представляет собой ломаную без самопересечений и самокасаний. В распоряжении кладоискателей имеется лебедка. Мощности лебедки хватает на то, чтобы двигать в определенном направлении без вращения каждую из частей, не поднимая ее, но не всю плиту целиком. Требуется по форме трещины определить, могут ли кладоискатели освободить люк.
Ввод из файла INPUT. TXT. В первой строке находится число N, задающее количество вершин ломаной. Следующие N строк содержат пары целых чисел — координаты вершин (Xi, Yi). Ломаная получается путем последовательного соединения точек в данном порядке. Направление обхода вершин ломаной может быть произвольным. Точки (X1 , Y1) и (XN , YN) лежат на одной или разных сторонах квадрата, остальные точки ломаной – внутри квадрата.
Ограничения: 3 ≤ N ≤ 100; -100 ≤ Xi ≤ 100; -100 ≤ Yi ≤ 100; время работы программы до 2 сек.
Вывод в файл OUTPUT. TXT. Выводится единственная строка со значением Yes или No – возможность либо невозможность разъединения квадрата путем перемещения его частей по плоскости без вращений.
Вывод 1 Вывод 2
Подсказка. Если разъединение существует, то его можно добиться перемещением какой-либо плиты в направлении одной из звеньев ломаной разреза.
11.6. Треугольники (6)
Роман достаточно давно занимается в математическом кружке, поэтому он уже успел узнать не только правила выполнения простейших операций, но и о таком достаточно сложном понятии как симметрия. Для того чтобы получше изучить симметрию, Роман решил начать с наиболее простых геометрических фигур – треугольников. Он скоро понял, что осевой симметрией обладают так называемые равнобедренные треугольники. Напомним, что треугольник называется равнобедренным, если его площадь положительна, и у него есть хотя бы две равные стороны.
Недавно Роман, зайдя в класс, увидел, что на доске нарисовано n точек. Разумеется, он сразу задумался, сколько существует троек из этих точек, которые являются вершинами равнобедренных треугольников.
Требуется написать программу, решающую указанную задачу.
Ввод из файла INPUT. TXT. В первой строке целое число n (3 ≤ n ≤ 1500). Каждая из последующих строк содержит по два разделенных пробелом целых числа – xi и yi , определяющих координаты i-ой точки. Все координаты точек не превосходят 109 по абсолютной величине. Среди заданных точек нет совпадающих.
Вывод в файл OUTPUT. TXT. В единственной строке необходимо вывести ответ.
Вывод 1 Вывод 2
Подсказка. Составим массив с длинами всех расстояний между точками. Для каждого элемента массива будем сохранять номера начальной и конечной точек. Таким образом, каждое ребро между двумя точками войдет в массив дважды. Для каждого ребра рассчитаем дополнительно угол наклона — против часовой стрелки от положительного направления оси X (значение от 0 до 2π).
Проведем быструю сортировку массива ребер в первую очередь по номеру начальной точки ребра, далее по их длине, а при одной и той же начальной точке и равных длинах по углу наклона.
Организуем просмотр отсортированного списка ребер. Два ребра могут быть сторонами очередного равнобедренного треугольника при выполнении следующих условий:
· ребра выходят из одной и той же вершины;
· ребра имеют равную длину;
· ребра не лежат на одной прямой, то есть образуют треугольник ненулевой площади;
Если некоторый треугольник равносторонний, то он будет посчитан 3 раза по каждой из своих вершин. Проще всего учитывать в процессе перебора количество равносторонних треугольников, чтобы в конце сделать необходимую поправку.
Гомотетией с центром O и коэффициентом k ¹ 0 называют преобразование плоскости, при котором точка O переходит сама в себя, а любая точка X ¹ O – в такую точку Y, что:
· Y лежит на прямой OX;
· при k >0 Y лежит на луче OX, при k 0.
С учетом описанных требований необходимо найти максимально возможную площадь равнобедренного треугольника, удовлетворяющего следующим условиям:
· основание треугольника лежит на оси абсцисс;
· основание симметрично относительно начала координат;
· треугольник полностью лежит внутри каждого из измеренных сечений заготовки.
Требуется написать программу, которая по заданным сечениям заготовки вычислит максимально возможную площадь искомого равнобедренного треугольника.
Ввод. Первая строка входного файла содержит целое число K – количество измеренных сечений. Далее следуют описания каждого из K сечений. В первой строке описания сечения содержится число NK – количество звеньев ломаной. За ней следуют (NK +1) строк, каждая из которых содержит пару целых чисел xi и yi – координаты вершин ломаной сечения в порядке их следования.
Вывод. Выходной файл должен содержать одно вещественное число – наибольшую возможную площадь треугольника. Эта площадь должна иметь абсолютную или относительную погрешность не более 10-6, что означает следующее. Пусть выведенное число равно x, а в правильном ответе оно равно y. Ответ будет считаться правильным, если значение выражения |x — y| / max<1, |y|> не превышает 10-6.
Видео:Видеоурок "Преобразование координат"Скачать

Заданы координаты вершин четырехугольника вывести их в порядке обхода по часовой стрелке
На плоскости заданы две точки A(x 1 ,y 1 ) и B(x 2 ,y 2 ). Определить, какой из отрезков — OA или OB образует больший угол с осью OX.
Принадлежит ли точка плоскости A отрезку с конечными точками B и C?
1. Выпуклый многоугольник задается координатами вершин при его обходе по часовой или против часовой стрелки. Контур многоугольника не имеет самопересечений. Определить направление обхода.
2. Выполнить то же самое, но только в случае невыпуклого многоугольника.
Отрезок на плоскости задается двумя не совпадающими концевыми точками X(x 1 ,x 2 ) и Y(y 1 ,y 2 ). Из точки Z(z 1 ,z 2 ) к прямой, содержащей отрезок [X,Y], проводится перпендикуляр P.
Определить, попадает ли перпендикуляр P на отрезок [X,Y] или на его продолжение.
Многоугольник на плоскости задается координатами своих N вершин в порядке обхода их по контуру по часовой стрелке. Считается, что контур самопересечений не имеет.
Найти площадь, периметр и углы многоугольника.
Определить, пересекается ли прямая ax+b=y и отрезок с концами (x 1 ,y 1 ), (x 2 ,y 2 ).
Отрезки на плоскости задаются парами целочисленных координат концевых точек. Определить, пересекаются ли 2 отрезка.
1. Треугольник на плоскости задается целочисленными координатами вершин. Для заданной точки Z(x,y) определить, принадлежит ли она стороне треугольника или лежит внутри или вне его.
2. Многоугольник на плоскости задается координатами своих N вершин в порядке обхода их по контуру по часовой стрелке (контур самопересечений не имеет). Для заданной точки Z(x,y) определить, принадлежит ли она стороне многоугольника или лежит внутри или вне его.
На плоскости заданы n отрезков координатами концевых точек. Концы отрезков задаются двумя парами координат (x 1 [i],y 1 [i]), (x 2 [i],y 2 [i]), 1
N точек на плоскости заданы своими координатами. Найти такой минимальный по площади выпуклый многоугольник, что все N точек лежат либо внутри этого многоугольника, либо на его границе (такой выпуклый многоугольник называется выпуклой оболочкой).
На решетке размера m*n заданы k точек своими координатами. Необходимо определить, можно ли построить выпуклый многоугольник такой, что каждая точка принадлежит некоторой стороне.
N точек на плоскости заданы своими координатами. Найти порядок, в котором можно соединить эти точки, чтобы получился N-угольник (т.е. не было бы пересечений сторон).
Представьте себе, что в тетрадке Вы зарисовали на листе какое-то количество клеточек и получили клеточную фигуру.
Сколько осей симметрии имеет заданная клеточная фигура.
1) Задается S — число тестов. Для каждого теста задаются N I размер фигуры по вертикали, N J — размер фигуры по горизонтали (N I J I строк из пробелов и единиц по N J символов в каждой строке.
2) Числа S, N I , N J занимают при вводе по три позиции.
2 ( количество тестов )
2 ( размер 1-ой фигуры по вертикали )
4 ( размер 1-ой фигуры по горизонтали )
3 ( размер 2-ой фигуры по вертикали )
5 ( размер 2-ой фигуры по горизонтали )
1-АЯ ФИГУРА ИМЕЕТ 1 ОСЕЙ СИММЕТРИИ
2-АЯ ФИГУРА ИМЕЕТ 0 ОСЕЙ СИММЕТРИИ
Прямоугольник ABCD задан координатами своих вершин. На противоположных сторонах AB и CD заданы последовательности R 1 и R 2 из N точек разбиения, а на сторонах BC и AD – R 3 и R 4 из M точек разбиения. Нумерация элементов последовательности R 1 и R 2 начинается соответственно от точек A и D, а в R 3 и R 4 — от B и A. Соединив отрезками точки с одинаковыми номерами в разбиениях R 1 и R 2 , а затем в разбиениях R 3 и R 4 , получим разбиение Q прямоугольника ABCD на множество четырехугольников. Построить алгоритм, определяющий четырехугольник разбиения Q с наибольшей площадью, при условии, что отрезки, соединяющие точки разбиений R 1 и R 2 параллельны стороне AD. Последовательности R 1 , R 2 , R 3 и R 4 задаются как массивы из длин отрезков разбиения соответствующих сторон прямоугольника.
На прямой задано N точек с координатами X 1 ,X 2 . X n . Написать программу, которая находит на прямой такую точку z, сумма расстояний от которой до данных N точек минимальна.
На двумерной плоскости задано N точек с координатами (X 1 ,Y 1 ), (X 2 ,Y 2 ), . (X n ,Y n ). Написать программу, которая находит такую точку Z(x,y), сумма расстояний от которой до остальных минимальна и:
а) Z — одна из заданных точек;
b) Z — произвольная точка плоскости.
На плоскости расположены N точек, заданные своими координатами. Найти на оси абсцисс точку, наибольшее из расстояний от которой до выбранных точек было бы минимальным.
На двумерной плоскости задано N точек с координатами (X 1 ,Y 1 ), (X 2 ,Y 2 ), . (X n ,Y n ). Написать программу, которая из этих точек выделяет вершины квадрата, содержащего максимальное число заданных точек.
ПРИМЕЧАНИЕ: предполагается, что точки, расположенные на сторонах квадрата, принадлежат ему.
Задано на плоскости множество из N прямоугольников, стороны которых параллельны осям координат, при этом каждый прямоугольник задается координатами левой нижней и правой верхней его вершин.
Составить алгоритм определения наибольшего натурального числа К, для которого существует точка плоскости, принадлежащая одновременно К прямоугольникам.
Примечание: эффективным считается алгоритм, число действий которого пропорционально Н 2 .
На квадратном торте N свечей. Можно ли одним прямолинейным разрезом разделить его на две равные по площади части, одна из которых не содержала бы ни одной свечи? Свечи будем считать точками, у которых известны их целочисленные координаты Х[1], Y[1]; . ; Х[N], Y[N] (начало координат — в центре торта); разрез не может проходить через свечу.
Даны N, N>1, прямоугольников, для которых предполагается, что:
А). Стороны любого прямоугольника параллельны координатным осям и прямоугольник задается концами одной из диагоналей.
В). Каждый прямоугольник имеет общие внутренние точки с хотя бы одним из остальных и не имеет общих вершин, сторон или частей сторон ни с одним из остальных прямоугольников.
Составить программу, которая решает следующие задачи:
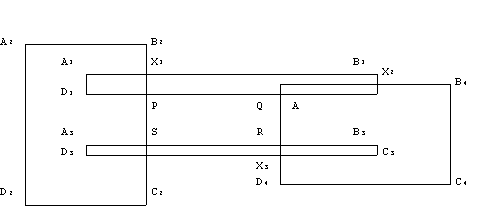
1. С помощью последовательности точек определить внешний контур фигуры F, являющейся объединением прямоугольников — ломаную замкнутую кривую. Пример на чертеже.
2. Определить содержит ли фигура F «дырки» ,т.е. замкнутые фигуры, которые ей не принадлежат.
3. Разложить фигуру на наименьшее возможное число не пересекающихся прямоугольников, которые могут иметь общие стороны или части сторон , а их объединение дает фигуру F.
4. Вычислить периметр и площадь фигуры F.
1. Задачи 3,4 решаются только для фигур, которые не содержат «дырки».
2. Полное решение содержит:
-анализ (обоснование) решения
-текст программы с соответствующими комментариями
-выполнение текстового примера, который будет дан при приемке работы
Объединение прямоугольников A i B i C i D i ,i=1,2,3,4 есть
фигура F=A 2 B 2 X 1 B 1 X 2 B 4 C 4 D 4 X 3 X 4 C 2 D 2
фигура F содержит единственную «дырку» PQRS
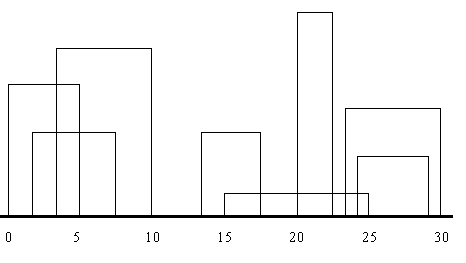
Необходимо написать программу — помощник архитектора в рисовании очертания города. Город задается расположением зданий. Город рассматривается как двумерный и все здания в нем — прямоугольники, имеющие одинаковое основание (город построен на равнине). Здания задаются тройкой чисел (L[i],H[i],R[i]) где L[i] и R[i] есть координаты левой и правой стен здания i, а H[i] — высота этого здания. На рисунке 1 здания описываются тройками
(1,11,5), (2,6,7), (3,13,9), (12,7,16), (14,3,25), (19,18,22), (23,13,29),(24,4,28)
а контур, показанный на рис. 2, задается последовательностью
(о способе формировании этой последовательности см. ниже).
Ввод представляет собой последовательность троек, задающих дома. Все координаты есть целые числа, меньшие 10000. Во входном файле минимум одно и максимум 50 зданий. Каждая тройка, обозначающая здание находится в отдельной строке во входном файле. Все целые числа в тройке разделены одним или несколькими пробелами. Тройки отсортированы по L[i], т.е. по левой х-координате здания, таким образом, здание с самой маленькой левой х-координатой является первым во входном файле.
Вывод будет состоять из вектора, описывающего очертание, как показано в примере выше. В векторе очертания (v[1],v[2],v[3], . , v[n-2],v[n-1],v[n]), v[i], когда i-четное число, означает горизонтальную линию (высоту). Когда i-нечетное, v[i]-означает вертикальную линию (х-координату). Вектор очертания будет определять маршрут, пройденный, к примеру, жуком, начавшим с минимальной х-координаты и путешествующим по всем вертикальным и горизонтальным линиям, определяющим контур. Последний элемент в векторе линии контура будет 0.
Нижняя левая и верхняя правая вершины прямоугольника A имеют координаты (0,0) и (V,W) соответственно. Множество S из N точек задается парами координат (x[i],y[i]), 1
2. Вывести результаты в виде
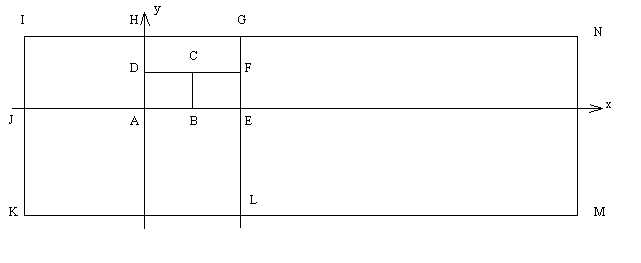
В первом квадранте координатной системы OXY нарисован первый квадрат — ABCD, длина стороны которого равна 1 и вершина A находится в начале координат. Потом нарисованы: второй квадрат — BEFC, третий — DFGH, четвертый — JAHI, пятый- KLEJ, шестой — LMNG, и так далее ‘по спирали’ (рис.1).
Написать программу, которая для введенных целых чисел x и y определяет и выводит номер квадрата, которому принадлежит точка P(x;y). Если точка P лежит на сторонах квадратов или в вершинах, то будем считать, что она принадлежит квадрату с наименьшим номером из возможных.
Примеры:
Результат
На плоскости N различных точек заданы своими координатами. Найти уравнение прямой, делящей это множество точек на 2 равномощных подмножества (т.е. на подмножества с одинаковым количеством элементов).
Найти пересечение и объединение двух выпуклых многоугольников. Многоугольники задаются координатами вершин в порядке обхода по контуру.
N-угольник на плоскости задается координатами вершин в порядке обхода по контуру (контур самопересечений не имеет). Для точки Z(x,y) найти минимальное расстояние до контура N-угольника.
На плоскости задано N точек своими координатами и матрица C(N*N); C(i,j)=C(j,i)=1 в случае, если вершины i и j соединены отрезком и 0 иначе. Известно, что любая вершина соединена по крайней мере с двумя другими, и что отрезки пересекаются только в концевых точках. Таким образом, вся плоскость разбивается на множество многоугольников. Задана точка Z(x,y). Найти минимальный по площади многоугольник, содержащий Z, или выдать сообщение, что такого не существует. Если Z принадлежит какому-то отрезку, то выдать его концевые точки, если Z лежит в многоугольнике, то выдать его вершины в порядке обхода по контуру.
Будем называть два многоугольника подобными, если существует взаимно-однозначное отображение сторон этих двух фигур такое, что соответствующие стороны пропорциональны с коэффициентом пропорциональности k, а углы, образованные двумя соответствующими сторонами, равны.
Определить, подобны ли два многоугольника. Многоугольники задаются на плоскости координатами вершин контуров. Вершины в контуре перечисляются в порядке обхода против часовой стрелки.
Примечание: так как все вычисления на ЭВМ проводятся с ограниченной точностью, то считать, что две величины равны если они совпадают с точностью до двух знаков после запятой.
Заданы натуральное N и две последовательности целых чисел (а 1 ,а 2 . а n ) и (b 1 ,b 2 . b n ). Заданы также два числа X 0 и X 1 , X 0 1 .
1. Найти числа t(0), t(1), . t(p), p 0 =t(0) 1 и указать для каждого отрезка [t(j-1), t(j)], 1 =аi*x+bi.
2.Найти числа s(0), s(1), . s(Q), таки, что X 0 =s(0) 1 , и указать для каждого отрезка [s(j-1),s(j)], 1 1 ,i 2 . i N ) чисел 1,2,3. N, что для всех x из [s(j-1),s(j)] справедливо неравенство
a i1 *x+b i1 i2 *x+b i2 iN *x+b iN
и для всех отрезков соответствующие перестановки различны.
На плоскости задано множество точек А и множество прямых В. Найти две такие различные точки из А, что проходящая через них прямая параллельна наибольшему количеству прямых из В.
В правильном n-угольнике провели несколько диагоналей, причем никакие три не пересекаются в одной точке. На сколько частей диагонали разбили n-угольник? Диагонали заданы номерами вершин n-угольника,которые они соединяют, все вершины перенумерованы по порядку числами 1, . n.
Круг разрезан несамопересекающейся ломаной, координаты вершин которой заданы парами натуральных чисел (x 1 ,y 1 ), . (x k ,y k ). Первая и последняя вершины лежат на границе круга, а остальные внутри его. Определить, можно ли разъединить две получившиеся части круга (выход из плоскости и повороты разнимаемых частей не допускается).
Среди треугольников с вершинами в заданном множестве точек на плоскости указать такой, стороны которого содержат максимальное число точек заданного множества.
Все стены дома имеют длину 5м. Северная и южная стороны-белые, западная и восточная-синие. Человек прошел от юго-восточного угла дома А метров на юг, В метров на восток и С метров север и посмотрел на дом.
Написать алгоритм, который определяет, что видит человек.
На местности, представляющей собой идеально ровную поверхность, стоит высокий забор. План забора представляет собой замкнутую ломаную без самопересечений. Эта ломаная задается N парами координат своих вершин в порядке обхода ограничиваемой забором области против часовой стрелки. Вершины пронумерованы от 1 до N, N
На гранях двух равных правильных тетраэдров N и M написаны числа N 1 ,N 2 ,N 3 ,N 4 и M 1 ,M 2 ,M 3 ,M 4 .
Можно ли совместить тетраэдры так, чтобы на совпадающих гранях оказались одинаковые числа?
📽️ Видео
Как решить любую задачу с четырёхугольниками? | Математика TutorOnlineСкачать

Найти периметр четырехугольника, вершины которого лежат на серединах сторон другого четырехугольникаСкачать

9 класс, 4 урок, Простейшие задачи в координатахСкачать

Нахождение координат вектора. Практическая часть. 9 класс.Скачать

Скалярное произведение векторов через координаты. 9 класс.Скачать

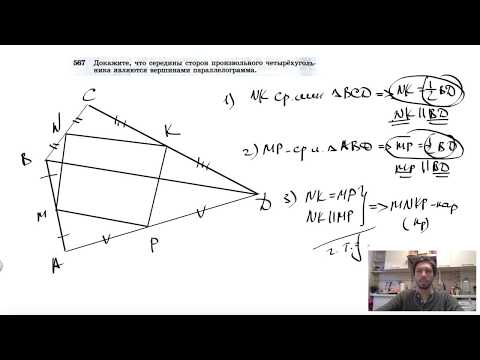
№567. Докажите, что середины сторон произвольного четырехугольника являютсяСкачать
Вписанные и описанные четырехугольники. Практическая часть. 9 класс.Скачать

Диагонали четырехугольника равны 4 и 5.Скачать

Алгоритмы и структуры данных 9. ГеометрияСкачать

Нахождение угла между векторами через координаты. 9 класс.Скачать

Алгоритмы. Пересечение отрезков.Скачать

Вписанные четырехугольники. 9 класс.Скачать