Центр окружности описанной около треугольника точка пересечения его высот

Ортоцентр — точка пересечения прямых, содержащих высоты треугольника.

Ортоцентр остроугольного треугольника лежит внутри треугольника.

Ортоцентр прямоугольного треугольника совпадает с вершиной прямого угла.

Ортоцентр тупоугольного треугольника лежит вне треугольника.

Свойства:

1. Точка, симметричная ортоцентру относительно стороны треугольника, лежит на описанной около него окружности.
   
2. Точка, симметричная ортоцентру относительно середины стороны треугольника, лежит на описанной окружности и диаметрально противоположна вершине треугольника, противолежащей стороне.
3. Расстояние от вершины треугольника до ортоцентра в два раза больше расстояния от центра описанной окружности до противолежащей стороны.
   
4. Сумма квадратов расстояния от вершины треугольника до ортоцентра и длины стороны, противолежащей этой вершине, равна квадрату диаметра описанной окружности.
5. Радиус описанной окружности, проведенный к вершине треугольника, перпендикулярен соответствующей стороне ортотреугольника.
   
6. При изогональном сопряжении ортоцентр переходит в центр описанной окружности.
   
7. Ортоцентр в остроугольном треугольнике является инцентром ортотреугольника.
   
8. Три отрезка прямых, соединяющих ортоцентр с вершинами остроугольного треугольника, разбивают его на три треугольника, имеющих равные радиусы описанных окружностей. При этом одинаковый радиус этих трех окружностей равен радиусу окружности, описанной около исходного остроугольного треугольника.
   

Видео:Окружность вписанная в треугольник и описанная около треугольника.Скачать

Планиметрия. Страница 3

Видео:Центр окружности описанной вокруг треугольникаСкачать

1.Окружность

Окружностью называется фигура, состоящая из множества точек на плоскости, равноудаленных от данной точки.

Эта данная точка называется центром окружности. Расстояние от центра окружности до ее точек называется радиусом окружности.

Отрезок, соединяющий две точки окружности, называется хордой.

Если хорда проходит через центр окружности, то она называется диаметром. (Рис.1)

ОА — радиус
ВС — диаметр
DE — хорда

Рис.1 Окружность, радиус, диаметр, хорда.

Видео:2038 центр окружности описанной около треугольника ABC лежит на стороне ABСкачать

2.Окружность, описанная около треугольника

Теорема: центр окружности, описанной около треугольника, является точкой пересечения перпендикуляров, опущенных на середины сторон данного треугольника.

Доказательство. Пусть АВС данный треугольник и точка О является центром окружности, описанной около данного треугольника. (Рис.2) Тогда отрезки ОА, ОВ, ОС равны как радиусы. Следовательно, треугольники Δ АОВ, Δ ВОС, Δ АОС — равнобедренные. А следовательно, и медианы, проведенные к серединам сторон ОК, ОЕ, ОD, являются одновременно биссектрисой и высотой. Поэтому предположение, что центр окружности, описанной около треугольника, является точкой пересечения высот, верно.

Рис.2 Теорема. Окружность, описанная около треугольника.

Видео:Точка O центр окружности описанной около остроугольного треугольникаСкачать

3.Окружность, вписанная в треугольник

Теорема. центр окружности, вписанной в треугольник, является точкой пересечения биссектрис, проведенных из его углов.

Доказательство. Пусть дан треугольник АВС. Точка О — центр вписанной окружности. (Рис. 3)

Тогда треугольник Δ АОЕ равен треугольнику Δ АОТ,
Δ СОЕ = Δ СОК,
Δ ВОК = Δ ВОТ.
Так как стороны ОА, ОВ, ОС у них общие. А ОК, ОЕ, ОТ как радиусы.
Следовательно:
∠ ЕАО = ∠ ТАО,
∠ ЕСО = ∠ КСО,
∠ КВО = ∠ ТВО.

Это значит, что точка О лежит на пересечении биссектрис АО, ВО, СО.

Рис.3 Теорема. Окружность, вписанная в треугольник.

Видео:Задание 16 ЕГЭ по математикеСкачать

4.Геометрическое место точек

Геометрическое место точек это фигура, которая представляет собой совокупность точек на плоскости, подчиняющихся определенному закону или обладающих определенным свойством.

Теорема. Геометрическим местом точек называется прямая, все точки которой равноудалены от двух данных точек, перпендикулярная отрезку, соединяющему эти точки и проходящая через его середину.

Доказательство. Пусть дан отрезок АС. Прямая А проходит через середину этого отрезка и перпендикулярна ему.(Рис. 4).

Тогда треугольники Δ АМВ и Δ СМВ равны. Так как сторона ВМ у них обшая, а стороны АМ и МС равны по условию. Следовательно точка В равноудалена от точек А и С.
Возьмем другую точку, например D, не лежащую на прямой а. Тогда сторона MD не принадлежит прямой а. А следовательно, углы AMD и DMC не равны т.к. не равны треугольники. Данное утверждение основано на том, что через точку, лежащую на прямой, можно провести только одну перпендикулярную ей прямую. И следовательно, расстояния от точки D до точек А и С не равны. Поэтому, для того чтобы расстояния от некой точки Х до двух данных точек были равны, необходимо чтобы она лежала на прямой а, которая перпендикулярна отрезку, соединяющего эти точки, и которая проходит через его середину.

Рис.4 Теорема. Геометрическое место точек.

Пример 1

Дана окружность с центром О. И проведена касательная а из точки С к этой окружности. Доказать, что точка К лежит на основании равнобедренного треугольника ОВС, если OB = 2R. (рис.5)

По условию прямая а есть касательная к окружности, следовательно радиус, проведенный к точке касания ОК, и который лежит на прямой с, составляет прямой угол с касательной. Так как ОВ = 2R и KB = R, то прямая а будет представлять собой геометрическое место точек, так как она перпендикулярна отрезку ОВ и проходит через его середину. А следовательно, треугольники ВКС и ОКС равны по первому признаку равенства треугольников. Отсюда можно сделать вывод, что точка К будет лежать на основании равнобедренного треугольника ВОС.

Рис.5 Задача. Дана окружность с центром О.

Пример 2

Докажите, что касательная к окружности не имеет с ней других общих точек, кроме точки касания. (Рис.6)

Доказательство:

Пусть дана окружность с центром в точке О. И прямая а, которая касается окружности в точке А. Допустим, что прямая а имеет еще одну точку касаная — точку В. Тогда радиус окружности, проведенный к точкам А и В образует угол с прямой а равный 90°.

Таким образом, в равнобедренном треугольнике АОВ углы при вершинах А и В равны 90°. А это невозможно. Следовательно, мы пришли к противоречию и прямая а не может касаться окружности в двух точках.

Рис.6 Задача. Касательная к окружности.

Пример 3

Точки А,В,С лежат на одной прямой, а точка О лежит вне этой прямой. Докажите, что треугольники АОВ и ВОС не могут быть равнобедренными с основаниями АВ и ВС. (Рис.7)

Доказательство:

Допустим, что треугольники АОВ и ВОС равнобедренные с основаниями АВ и ВС. Тогда Стороны АО, ВО и СО равны. Отсюда следует, что углы ОАВ, АВО, ОВС и ОСВ равны. И ∠АВО = ∠ОВС = 90°, так как эти углы являются смежными, а их сумма равна 180°.

Таким образом, в равнобедренных треугольниках АОВ и ВОС углы при вершинах А и С равны 90°. А это невозможно, потому, что тогда стороны АО, ВО и СО были бы параллельны, так как они перпендикулярны одной прямой АС. Следовательно, мы пришли к противоречию, и треугольники АОВ и ВОС не могут быть равнобедренными с основаниями АВ и ВС.

Рис.7 Задача. Даны три точки на прямой.

Пример 4

Окружности с центрами О и О₁ пересекаются в точках А и В. Докажите, что прямая АВ перпендикулярна прямой ОО₁ (Рис.8)

Доказательство:

Так как окружности пересекаются в точках А и В, то эти две точки принадлежат обеим окружностям. Следовательно, отрезок ОА = ОВ, как радиусы окружности с центром в точке О. А отрезок О₁А = О₁В, как радиусы окружности с центром в точке О₁.

Таким образом, треугольники ОАО₁ и ОВО₁ равны по третьему признаку равенства треугольников (по трем сторонам). А следовательно отрезки АС и ВС равны. И прямая ОО₁ является геометрическим местом точек для двух данных точек А и В. Т.е. любая точка прямой ОО₁ равноудалена от двух данных точек А и В. Следовательно, треугольники ОАС и ОВС равны, также как и треугольники АСО₁ и ВСО₁ по трем сторонам. А отсюда следует равенство углов при вершине С. Т.е. ∠ОСА = ∠ОСВ = ∠АСО₁ = ∠ВСО₁ = 90°.

Следовательно, можно сделать вывод, что прямая АВ перпендикулярна прямой ОО₁.

Рис.8 Задача. Окружности с центрами О и О₁.

Пример 5

Отрезок ВС пересекает прямую а в точке О. Расстояние от точек В и С до прямой а равны. Докажите, что точка О является серединой отрезка ВС (Рис.9)

Доказательство:

По условию задачи, расстояния от точек В и С до прямой а равны. Т.е. РС = BQ. Так как расстояние от точки до прямой представляет собой перпендикуляр, то два треугольника РОС и ВОQ, образованные двумя пересекающимися прямыми ВС и а, и перпендикулярами, опущенными на одну из них, равны по второму признаку равенства треугольников ( по стороне и двум прилегающим к ней углам: РС = BQ, углы при вершинах В и С равны как внутренние накрест лежащие, а углы при вершинах Р и Q прямые).

Из равенства треугольников РОС и ВОQ следует, что ВО = ОС.

Рис.9 Задача. Отрезок ВС пересекает прямую а .

Видео:✓ Самая сложная задача в ОГЭ-2020 | Задание 26. Математика | Геометрия | Борис ТрушинСкачать

Окружность, описанная около треугольника

Видео:Геометрия Радиус окружности описанной около треугольника ABC равен 6 см Найдите радиус окружностиСкачать

Определение окружности, описанной около треугольника

Определение 1. Окружностью, описанной около треугольника называется окружность, проходящей через все три вершины треугольника (Рис.1).

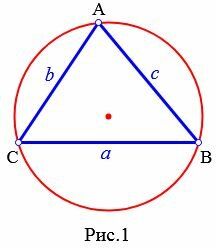При этом треугольник называется треугольником вписанным в окружность .

Видео:ОГЭ 2019. Задание 17. Разбор задач. Геометрия. Окружность.Скачать

Теорема об окружности, описанной около треугольника

Теорема 1. Около любого треугольника можно описать окружность.

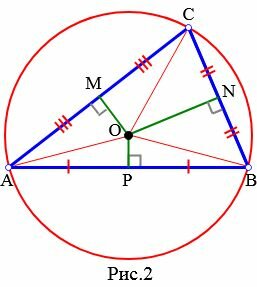Доказательство. Пусть задан произвольный треугольник ABC (Рис.2). Обозначим точкой O точку пересечения серединных перпендикуляров к его сторонам. Проведем отрезки OA, OB и OC. Поскольку точка O равноудалена от точек A, B и C, то OA=OB=OC. Тогда окружность с центром O и радиусом OA проходит через все три вершины треугольника ABC и, следовательно, является окружностью, описанной около треугольника ABC.

Из теоремы 1 следует, что центром описанной около треугольника окружности является точка пересечения серединных перпендикуляров к сторонам треугольника.

Замечание 1. Около любого треугольника можно описать только одну окружность.

Доказательство. Допустим, что около треугольника можно описать две окружности. Тогда центр каждой из этих окружностей равноудален от вершин треугольника и совпадает с точкой O пересечения серединных перпендикуляров сторон треугольника. Радиус этих окружностей равен расстоянию от точки O до вершин треугольника. Поэтому эти окружности совпадают.

📽️ Видео

Замечательные точки треуг-ка. 8 класс.Скачать

Уравнение окружности описанной около треугольникаСкачать

Через центр О окружности, описанной около остроугольного треугольника ДВИ МГУСкачать

Построить описанную окружность (Задача 1)Скачать

Всё про углы в окружности. Геометрия | МатематикаСкачать

Центром окружности, описанной около треугольника ... | ОГЭ 2017 | ЗАДАНИЕ 13 | ШКОЛА ПИФАГОРАСкачать

✓ Расстояние от вершины треугольника до точки пересечения высот | Ботай со мной #113 | Борис ТрушинСкачать

Разбор Задачи №16 из Варианта Ларина №271Скачать

ЕГЭ Задание 16 Первый признак подобия треугольниковСкачать

№203. Через центр О окружности, вписанной в треугольник ABC, проведена прямая ОK, перпендикулярнаяСкачать

№706. Найдите сторону равностороннего треугольника, если радиус описанной около него окружностиСкачать

Вписанные и описанные окружности. Вебинар | МатематикаСкачать