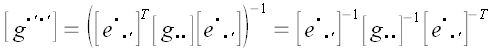Вектора a и b называются ортогональными, если угол между ними равен 90°. (рис. 1).
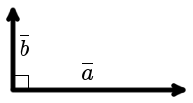 |
| рис. 1 |
- Примеры задач на ортогональность векторов
- Примеры плоских задач на ортогональность векторов
- Примеры пространственных задач на ортогональность векторов
- Ортогональные векторы и условие ортогональности
- Ортогональные векторы: определение и условие
- Примеры решения задач на ортогональность векторов
- Плоские задачи на ортогональность векторов
- Примеры пространственных задач на ортогональность векторов
- Взаимно ортогональные вектора это
- 💥 Видео
Видео:Ортогональность. ТемаСкачать

Примеры задач на ортогональность векторов
Примеры плоских задач на ортогональность векторов
Так в случае плоской задачи для векторов a = < ax ; ay > и b = < bx ; by > , условие ортогональности запишется следующим образом:
Найдем скалярное произведение этих векторов:
a · b = 1 · 2 + 2 · (-1) = 2 — 2 = 0
Ответ: так как скалярное произведение равно нулю, то вектора a и b ортогональны.
Найдем скалярное произведение этих векторов:
a · b = 3 · 7 + (-1) · 5 = 21 — 5 = 16
Ответ: так как скалярное произведение не равно нулю, то вектора a и b не ортогональны.
Найдем скалярное произведение этих векторов:
a · b = 2 · n + 4 · 1 = 2 n + 4
2 n + 4 = 0
2 n = -4
n = -2
Ответ: вектора a и b будут ортогональны при n = -2.
Примеры пространственных задач на ортогональность векторов
Так в случае пространственной задачи для векторов a = < ax ; ay ; az > и b = < bx ; by ; bz >, условие ортогональности запишется следующим образом:
Найдем скалярное произведение этих векторов:
a · b = 1 · 2 + 2 · (-1) + 0 · 10 = 2 — 2 + 0 = 0
Ответ: так как скалярное произведение равно нулю, то вектора a и b ортогональны.
Найдем скалярное произведение этих векторов:
a · b = 2 · 3 + 3 · 1 + 1 · (-9) = 6 + 3 -9 = 0
Ответ: так как скалярное произведение равно нулю, то вектора a и b ортогональны.
Найдем скалярное произведение этих векторов:
a · b = 2 · n + 4 · 1 + 1 · (-8)= 2 n + 4 — 8 = 2 n — 4
2 n — 4 = 0
2 n = 4
n = 2
Ответ: вектора a и b будут ортогональны при n = 2.
Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!
Добро пожаловать на OnlineMSchool.
Меня зовут Довжик Михаил Викторович. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики.
Видео:Компланарны ли векторы: a=(2;5;8), b=(1;-3;-7) и c=(0;5;10)?Скачать

Ортогональные векторы и условие ортогональности
В данной статье мы расскажем, что такое ортогональные векторы, какие существуют условия ортогональности, а также приведем подробные примеры для решения задач с ортогональными векторами.
Видео:2 42 Ортогональность векторовСкачать

Ортогональные векторы: определение и условие
Ортогональные векторы — это векторы a ¯ и b ¯ , угол между которыми равен 90 0 .
Необходимое условие для ортогональности векторов — два вектора a ¯ и b ¯ являются ортогональными (перпендикулярными), если их скалярное произведение равно нулю.
Видео:18+ Математика без Ху!ни. Скалярное произведение векторов. Угол между векторами.Скачать

Примеры решения задач на ортогональность векторов
Плоские задачи на ортогональность векторов
Если дана плоская задача, то ортогональность для векторов a ¯ = и b ¯ = записывают следующим образом:
a ¯ × b ¯ = a x × b x + a y × b y = 0
Задача 1. Докажем, что векторы a ¯ = и b ¯ = ортогональны.
Как решить?
Находим скалярное произведение данных векторов:
a ¯ × b ¯ = 1 × 2 + 2 × ( — 1 ) = 2 — 2 = 0
Ответ: поскольку произведение равняется нулю, то векторы являются ортогональными.
Задача 2. Докажем, что векторы a ¯ = и b ¯ = ортогональны.
Как решить?
Находим скалярное произведение данных векторов:
a ¯ × b ¯ = 3 × 7 + ( — 1 ) × 5 = 21 — 5 = 16
Ответ: поскольку скалярное произведение не равняется нулю, то и векторы не являются ортогональными.
Задача 3. Найдем значение числа n , при котором векторы a ¯ = и b ¯ = будут ортогональными.
Как решить?
Найдем скалярное произведение данных векторов:
a ¯ × b ¯ = 2 × n + 4 × 1 = 2 n + 4 2 n + 4 = 0 2 n = — 4 n = — 2
Ответ: векторы являются ортогональными при значении n = 2 .
Видео:Ортогональная проекция и ортогональная составляющая. ТемаСкачать

Примеры пространственных задач на ортогональность векторов
При решении пространственной задачи на ортогональность векторов a ¯ = и b ¯ = условие записывается следующим образом: a ¯ × b ¯ = a x × b x + a y × b y + a z × b z = 0 .
Задача 4. Докажем, что векторы a ¯ = и b ¯ = являются ортогональными.
Как решить?
Находим скалярное произведение данных векторов:
a ¯ × b ¯ = 1 × 2 + 2 × ( — 1 ) + 0 × 10 = 2 — 2 = 0
Ответ: поскольку произведение векторов равняется нулю, то они являются ортогональными.
Задача 5. Найдем значение числа n , при котором векторы a ¯ = и b ¯ = будут являться ортогональными.
Как решить?
Находим скалярное произведение данных векторов:
a ¯ × b ¯ = 2 × n + 4 × 1 + 1 × ( — 8 ) = 2 n + 4 — 8 = 2 n — 4 2 n — 4 = 0 2 n = 4 n = 2
Ответ: векторы a ¯ и b ¯ будут ортогональными при значении n = 2 .
Видео:A.7.4 Ортогонализация набора векторов. Процесс Грама-Шмидта.Скачать

Взаимно ортогональные вектора это
В. Г. Автор. Векторная и тензорная алгебра для будущих физиков и техников
.Геометрическое определение вектора
.Алгебраические операции над направленными отрезками
..Сложение направленных отрезков
..Умножение направленных отрезков на число
..Параллельное проектирование вектора в пространстве
. Проекция точки на плоскость
. Проекция вектора на плоскость
..Ортогональная проекция вектора в пространстве
. Ортогональная проекция вектора на плоскость
. Ортогональная проекция вектора на прямую и направленную ось
..Векторы в трехмерном геометрическом пространстве
..Линейная зависимость векторов и размерность пространства
..Различные формы записи векторов
..Линейные операции над векторами в координатной форме
. Свойства скалярного умножения
. Скалярное умножение в декартовых координатах
..Некоторые примеры использования скалярного умножения
..Площадь параллелограмма, построенного на векторах
..Задачи на применение определителей
..Определитель третьего порядка и его свойства
..Векторное умножение векторов базиса декартовой системы координат
.Взаимный координатный базис
.Ковариантные и контравариантные координаты вектора
..Индексная форма записи для выражений с определителями
..Свойства символов Веблена
..Операция векторного умножения в произвольных косоугольных координатах
.Линейный оператор и его матрица
.Доказательство теоремы об определителе
.Общие определения алгебраических операций с тензорами
.Примеры на применение тензоров в физике
..Задачи на тождественные преобразования
Вернемся к задаче вычисления скалярного произведения в произвольной косоугольной системе координат 




и в общем случае ни один из коэффициентов 













Заручившись поддержкой вспомогательной системы координат, которую принято называть взаимной , мы получаем максимально простое выражение для скалярного умножения.
Сама же взаимная система координат полностью определяется основной системой и условиями 
1. Каждый базисный вектор взаимной системы ортогонален ко всем разноименным с ним базисным векторам основной системы.
2. Длина базисного вектора взаимной системы выбирается таким образом, чтобы скалярное произведение его на одноименный вектор основной системы равнялось единице.
Сами векторы взаимного базиса удобнее всего вычислить через их координаты. Координаты можно вычислить либо в основном базисе, либо в некотором вспомогательном. Мы используем обе эти возможности. Для начала покажем, как можно вычислить координаты векторов взаимного базиса во вспомогательной декартовой системе координат. Воспользуемся тем, что

Пусть 


Умножив правую и левую часть уравнения на матрицу



То есть матрица координат взаимного базиса равна обратной и транспонированной матрице координат основного базиса в некоторой декартовой системе координат.
Рассмотрим простой в вычислительном отношении пример на нахождение взаимного базиса для системы координат на плоскости.

Пусть векторы основного базиса 








Нахождение взаимного базиса в пространстве усложняется только за счет процедуры вычисления обратной матрицы, других принципиальных отличий нет.
Теперь воспользуемся другой более общей возможностью и выразим векторы взаимного базиса через векторы основного: 


В свое время для скалярного произведения векторов основного базиса мы ввели обозначение 


Теперь равенство 







Вернемся к нахождению векторов взаимного базиса.
Пусть 




Найдем координаты метрического тензора в основном и во взаимном базисах.


И, воспользовавшись уравнением 




Основная и взаимная системы координат связаны друг с другом соотношениями 

которое принято называть ковариантным преобразованием. Соответственно и векторы основного базиса, и индексы, которыми они пронумерованы, называются ковариантными.
Координаты вектора в основной системе координат изменяются в соответствии с другим законом:

который называется контравариантным. Матрица, определяющая контравариантное преобразование, является обратной и транспонированной по отношению к матрице ковариантного преобразования:

С этим и связан выбор названий – ковариантный и контравариантный . Соответственно и координаты вектора в основной системе координат, и индексы, которыми они пронумерованы, называются контравариантными. Ковариантные индексы принято писать внизу, а контравариантные – вверху. Мы с самого начала старались придерживаться этого правила, хотя до настоящего момента нам было сложно объяснить причину необычного для индекса верхнего положения.
Мы пока еще не пытались выяснить законы преобразования векторов взаимного базиса и координат векторов в этом базисе, но если принятые нами обозначения не являются случайными, то векторы взаимного базиса 







Здесь мы использовали известный закон преобразования ковариантных координат метрического тензора.

Умножаем на 


Матрицы 




При свертке 



Свертываем правую и левую части равенства с 


Свертываем с 


В этом выводе мы постарались продемонстрировать некоторые часто используемые приемы работы с индексами. Матричный перевод мы привели только в порядке пояснения, поскольку действия с матрицами более привычны. В данном случае преобразования в индексной форме не очень эффективны, поскольку мы вынуждены несколько раз последовательно выполнять операцию свертки. Выполняя те же преобразования только в матричной форме, мы быстрее приходим к результату. Покажем это на сей раз без комментариев.

А так как 


Приведем для сравнения оба закона вместе.




Теперь перейдем к законам преобразования для векторов взаимного базиса и ковариантных координат вектора.


А что мы можем сказать про ковариантные координаты вектора, то есть про координаты вектора во взаимном базисе? До сих пор мы говорили только про сам базис, и еще ни разу не представилась возможность поговорить о координатах. Начнем с того, что мы знаем, то есть с контравариантных координат.
Пусть 




Операции, которые мы свели в таблицу, принято называть операциями поднятия и опускания индексов. Часто используют более образное название – » жонглирование индексами «. Операции по жонглированию индексами выполняются при помощи метрического тензора и позволяют легко переходить от ковариантных координат к контравариантным, и наоборот.
Перейдем к законам преобразования ковариантных координат вектора при изменении системы координат.
Пусть 


Сведем законы преобразования для векторов базиса и координат векторов в одну таблицу.
💥 Видео
ОртогональностьСкачать

Коллинеарные векторы.Скачать

Коллинеарность векторовСкачать

Лекция 16. Понятие вектора и векторного пространства. Базис векторного пространства.Скачать

Высшая математика. Линейные пространства. Векторы. БазисСкачать

Зачем нужен ВЕКТОР. Объяснение смыслаСкачать

Понятие вектора. Коллинеарные вектора. 9 класс.Скачать

Математика без Ху!ни. Смешанное произведение векторовСкачать

Вектор. Сложение и вычитание. 9 класс | МатематикаСкачать

Что такое вектора? | Сущность Линейной Алгебры, глава 1Скачать

Как разложить вектор по базису - bezbotvyСкачать

§48 Ортонормированный базис евклидова пространстваСкачать

12.2 Ортогональные преобразования IIСкачать

Аналитическая геометрия, 1 урок, Векторы в пространствеСкачать