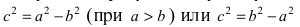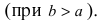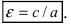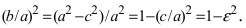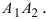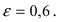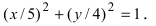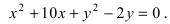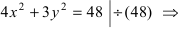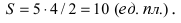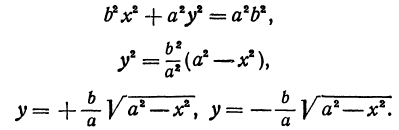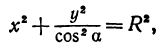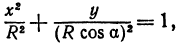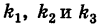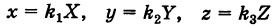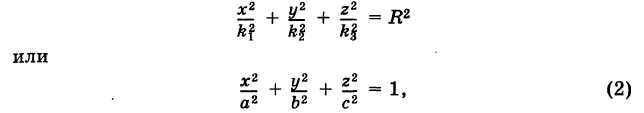Условие
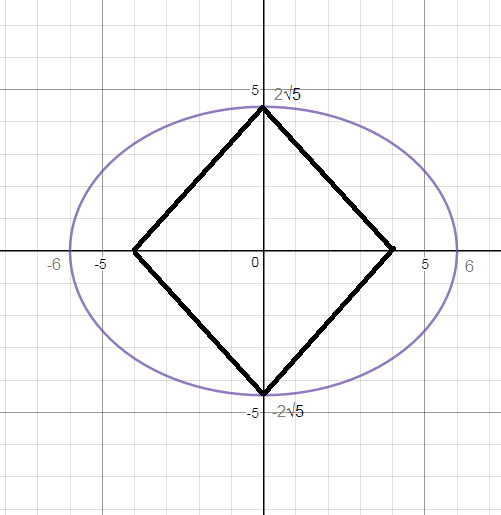
4. Найти площадь четырехугольника, две вершины которого лежат в фокусах эллипса 5x^2+9y^2-180=0, а две другие совпадают с концами его малой оси.
Решение
Запишем каноническое уравнение эллипса
(x^2)/(180/5)+(y^2)/(180/9)=1
или
(x^2)/(36)+(y^2)/(20)=1
О т в е т. 16sqrt(5)
Почему корень20=2корен5 4корен5
20=4*5 √20=(√4)*√5=2*√5 Длина диагонали 4√5=2√5-(-2√5)
Видео:165. Найти фокусы и эксцентриситет эллипса.Скачать

Разные задачи. Эллипс
№ 8.1 Составить уравнение эллипса, фокусы которого лежат на оси ОХ симметрично относительно начала координат, зная, что:
- 1) его полуоси равны 5 и 2;
- 2) его большая ось равна 10, а расстояние между фокусами 2с = 8;
- 3) его малая ось 24, а расстояние между фокусами 10;
- 4) расстояние между его фокусами 2с = 6 и е = 3/5;
- 5) его большая ось 20, а эксцентриситет е — 3/5′,
- 6) его малая ось 10, а эксцентриситет е = 12/13;
- 7) расстояние между директрисами 5, между фокусами 4;
- 8) его большая ось 8, а расстояние между директрисами 16;
- 9) его малая ось 6, а расстояние между директрисами 13;
- 10) расстояние между его директрисами 32 и е = 1/2.
№ 8.2 Составить уравнение эллипса, фокусы которого лежат на оси OY симметрично относительно начала координат, зная, что:
- 1) его полуоси равны 7 и 2;
- 2) его большая ось равна 10, а расстояние между фокусами 2с = 8;
- 3) расстояние между его фокусами 2с = 24 и эксцентриситет 12/13;
- 4) его малая ось равна 16, а эксцентриситет 3/5;
- 5) расстояние между фокусами 6 и между директрисами 50/3;
- 6) расстояние между директрисами 32/3 и эксцентриситет 3/4.
№ 8.3 Дан эллипс 9т 2 + 25г/ 2 — 225. Найти: 1) его полуоси;
2) фокусы; 3) эксцентриситет; 4) уравнения директрис.
№ 8.4 Вычислить площадь четырёхугольника, две вершины которого лежат в фокусах эллипса ж 2 + 5у 2 = 20, а две другие совпадают с концами его малой оси.
№ 8.5 Дан эллипс 9т 2 + 5г/ 2 = 45. Найти: 1) его полуоси;
2) фокусы; 3) эксцентриситет; 4) уравнения директрис.
№ 8.6 Вычислить площадь четырёхугольника, две вершины которого лежат в фокусах эллипса 9ж 2 + 5у 2 = 1, а две другие совпадают с концами его малой оси.
№ 8.7 Вычислить расстояние от фокуса F(c;0) эллипса + =
а 1 о 2 = 1 до односторонней с этим фокусом директрисы.
№ 8.8 На эллипсе — + = 1 найти точки, абсцисса которых —3.
№ 8.9 Эксцентриситет эллипса е = 2/3, фокальный радиус точки М эллипса равен 10. Вычислить расстояние от точки М до односторонней с этим фокусом директрисы.
№ 8.10 Эксцентриситет эллипса е = 2/5, расстояние от точки М эллипса до директрисы равно 20. Вычислить расстояние от точки М ней с данным фокусом.
до фокуса, одностороннего с этой директрисой.
№ 8.11 Дана точка Mi(2;—5/3) на эллипсе —+у- = 1. Составить уравнения прямых, на которых лежат фокальные радиусы точки М.
№ 8.12 Убедившись, что точка Mi(—4:2,4) лежит на эллипсе — + 25
Ч—= 1, найти фокальные радиусы точки Mi.
№ 8.13 Эксцентриситет эллипса е = 1/3, центр его совпадает с началом координат, один из фокусов (—2;0). Вычислить расстояние от точки М эллипса с абсциссой, равной 2, до директрисы, односторон
№ 8.14 Эксцентриситет эллипса е = 1/2, центр его совпадает с началом координат, одна из директрис дана уравнением х = 16. Вычислить расстояние от точки Mi эллипса с абсциссой —4 до фокуса, одностороннего с данной директрисой.
№ 8.15 Определить точки эллипса —1- — = 1, расстояние
которых до правого фокуса равно 14.
№ 8.16 Определить точки эллипса—h — = 1, расстояние
которых до левого фокуса равно 2,5.
№ 8.17 Через фокус эллипса — + ^7 = 1 проведен перпендикуляр к его большой оси. Определить расстояния от точек пересечения этого перпендикуляра с эллипсом до фокусов.
№ 8.18 Составить уравнение эллипса, фокусы которого расположены на оси абсцисс симметрично относительно начала координат, если даны:
- 1) точка Mi<—2/5; 2) эллипса и его малая полуось 6 = 3;
- 2) точка Mi(2; —2) эллипса и его большая полуось а = 4;
- 3) точки 7И1(4;-/3) и Л/2(2л/2; 3) эллипса;
- 4) точка 7И1(д/15;—1) эллипса и расстояние между фокусами 8;
- 5) точка Л?1(2;—5/3) эллипса и его эксцентриситет е = 2/3;
- 6) точка Mi(8; 12) эллипса и п = 20 от нее до левого фокуса;
- 7) точка М1(—2) эллипса и расстояние между директрисами 10.
№ 8.19 Определить эксцентриситет е эллипса, если:
- 1) его малая ось видна из фокусов под углом 60°;
- 2) отрезок между фокусами виден из вершин малой оси под прямым углом;
- 3) расстояние между директрисами в три раза больше расстояния между фокусами;
- 4) отрезок перпендикуляра, опущенного из центра эллипса на его директрису, делится вершиной эллипса пополам.
№ 8.20 Через фокус F эллипса проведён перпендикуляр к его большой оси. Определить, при каком значении эксцентриситета эллипса отрезки АВ и ОС будут параллельны.
№ 8.21 Составить уравнение эллипса с полуосями а, b и центром С(хо,уо), если оси симметрии эллипса параллельны осям координат.
№ 8.22 Эллипс касается оси ОХ в точке А(3; 0) и оси OY в точке В(0; — 4). Составить уравнение этого эллипса, зная, что его оси симметрии параллельны координатным осям.
№ 8.23 Точка С(—3; 2) является центром эллипса, касающегося обеих координатных осей. Составить уравнение этого эллипса, зная, что его оси симметрии параллельны координатным осям.
№ 8.24 Составить уравнение эллипса, зная, что:
- 1) его большая ось равна 26 и фокусы 7 7 i(—10; 0), 2*2(14; 0);
- 2) его малая ось равна 2 и фокусы Fi(—1; —1), F2(l; 1);
- 3) его фокусы Fi(—2;3/2), F2(2; -3/2) и е = /2/2;
- 4) фокусы Fi(l; 3), F2(3;l), расстояние между директрисами 12-/2.
№ 8.25 Составить уравнение эллипса, если известны его е = 2/3, фокус F(2; 1) и уравнение соответствующей директрисы х — 5 — 0.
№ 8.26 Составить уравнение эллипса, если известны е = 1/2, фокус F(—4; 1) и уравнение соответствующей директрисы у -I- 3 = 0.
№ 8.27 Точка А(—3; —5) лежит на эллипсе, фокус которого
F(l; —4), а соответствующая директриса х — 2 = 0. Составить уравнение этого эллипса.
№ 8.28 Составить уравнение эллипса, если известны его е = 1/2, F(3; 0) и уравнение соответствующей директрисы х + у — 1 = 0.
№ 8.29 Точка Mi(2; -1) лежит на эллипсе, фокус которого F(l,0), а соответствующая директриса дана уравнением 2х — у — 10 = 0. Составить уравнение эллипса.
№ 8.30 Точка Л2Т(3; — 1) является концом малой оси эллипса, фокусы которого лежат на прямой у + 6 = 0. Составить уравнение этого эллипса, зная его е = д/2/2.
Для решения см. пример аналогичной задачи на с. 91. Ответы на с. 252.
Видео:§17 Определение эллипсаСкачать

Эллипс — определение и вычисление с примерами решения
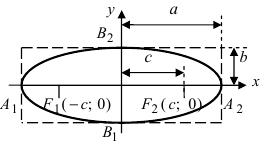
Эллипс:
Определение: Эллипсом называется геометрическое место точек, сумма расстояний от которых до двух выделенных точек
Получим каноническое уравнение эллипса. Выберем декартову систему координат так, чтобы фокусы
Рис. 29. Вывод уравнения эллипса.
Расстояние между фокусами (фокусное расстояние) равно 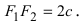
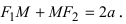
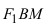
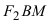
соответственно. Следовательно, согласно определению имеем
Возведем обе части равенства в квадрат, получим
Перенося квадратный корень в левую часть, а все остальное в правую часть равенства, находим 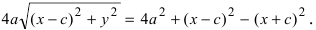
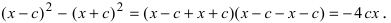
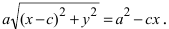
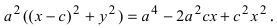
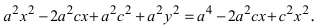
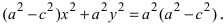
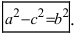
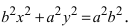
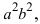
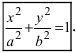
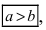
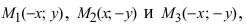
т.е. точками пересечения эллипса с осью абсцисс будут точки
т.е. точками пересечения эллипса с осью ординат будут точки
(Рис. 30).
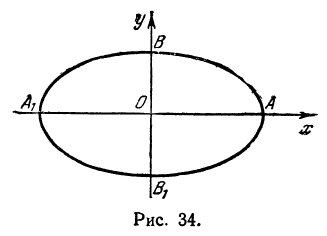
Определение: Найденные точки называются вершинами эллипса.
Рис. 30. Вершины, фокусы и параметры эллипса
Определение: Если 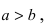
Определение: Эксцентриситетом эллипса называется отношение фокусного рас- стояния к большой полуоси эллипса
Из определения эксцентриситета эллипса следует, что он удовлетворяет двойному неравенству 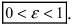
Если 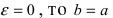
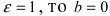
Пример:
Составить уравнение эллипса, если его большая полуось а = 5, а его эксцентриситет
Решение:
Исходя из понятия эксцентриситета, найдем абсциссу фокуса, т.е. параметр 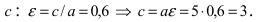
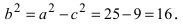
Пример:
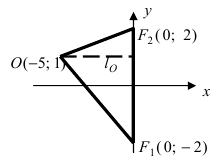
Найти площадь треугольника, две вершины которого находятся в фокусах эллипса 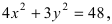
Решение:
Для определения координат фокусов эллипса и центра окружности преобразуем их уравнения к каноническому виду. Эллипс:
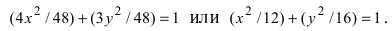
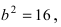
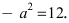
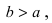
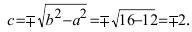
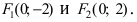
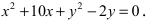
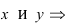
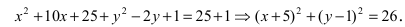
Построим в декартовой системе координат треугольник 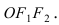
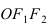
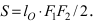
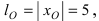
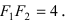
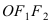
Видео:Математика без Ху!ни. Кривые второго порядка. Эллипс.Скачать

Эллипс в высшей математике
где 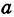
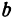
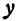
Отсюда видно, что уравнение (2) определяет две функции. Пока независимое переменное 
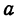

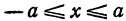
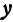
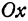
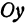
При 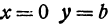
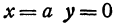
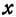

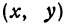
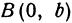
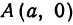
Полученная линия называется эллипсом. Число 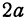
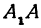
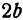
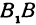
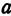
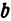
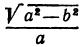
Пример:
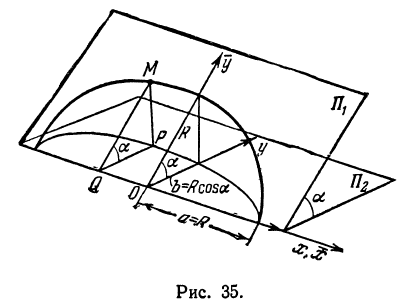
Найти проекцию окружности на плоскость, не совпадающую с плоскостью окружности.
Решение:
Возьмем две плоскости, пересекающиеся под углом 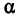
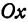
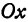
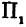
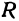
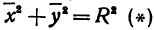
Пусть точка 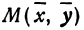
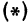
Обозначим проекцию точки 
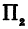
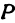
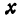
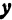


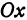
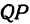
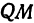
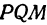
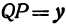
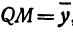
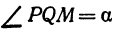
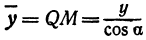


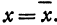
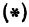
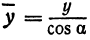
а это есть уравнение эллипса с полуосями 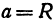
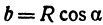
Таким образом, эллипс является проекцией окружности на плоскость, расположенную под углом к плоскости окружности.
Замечание. Окружность можно рассматривать как эллипс с равными полуосями.
Видео:Площадь эллипсоида + вывод формулы площади поверхности вращенияСкачать

Уравнение эллипсоида
Определение: Трехосным эллипсоидом называется поверхность, полученная в результате равномерной деформации (растяжения или сжатия) сферы по трем взаимно перпендикулярным направлениям.
Рассмотрим сферу радиуса R с центром в начале координат:
где Х, У, Z — текущие координаты точки сферы.
Пусть данная сфера подвергнута равномерной деформации в направлении координатных осей 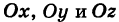
В результате сфера превратится в эллипсоид, а точка сферы М (X, У, Z) с текущими координатами Х, У, Z перейдет в точку эллипсоидам 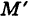
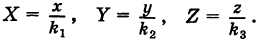
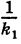
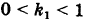
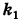
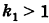
Подставляя эти формулы в уравнение (1), будем иметь
где 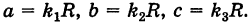
Величины 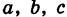
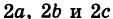
Если две полуоси эллипсоида равны между собой, то эллипсоид называется эллипсоидом вращения, так как может быть получен в результате вращения эллипса вокруг одной из его осей. Например, в геодезии считают поверхность земного шара эллипсоидом вращения с полуосями
а = b = 6377 км и с = 6356 км.
Если а = b = с, то эллипсоид превращается в сферу.
| Рекомендую подробно изучить предметы: |
|
| Ещё лекции с примерами решения и объяснением: |
- Гипербола
- Парабола
- Многогранник
- Решение задач на вычисление площадей
- Шар в геометрии
- Правильные многогранники в геометрии
- Многогранники
- Окружность
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
🔍 Видео
Площадь эллипса без интегралаСкачать

Геометрия 8. Урок 12 - Площадь четырехугольников. Формулы.Скачать

§28 Эксцентриситет эллипсаСкачать

Математика без Ху!ни. Смешанное произведение векторовСкачать

Аналитическая геометрия: Эллипс, Парабола, Гипербола. Высшая математикаСкачать

Всё про углы в окружности. Геометрия | МатематикаСкачать

Четырехугольники, вписанные в окружность. 9 класс.Скачать

Математика без Ху!ни. Уравнение плоскости.Скачать

Аналитическая геометрия, 7 урок, Линии второго порядкаСкачать

Вычислить ➜ (10!-9!-8!)/(10!+9!+8!)Скачать

174. Фокальные расстояния точек эллипса.Скачать

Эллипс | Элементы аналитической геометрииСкачать

ЭллипсСкачать

Аналитическая геометрия: окружность и эллипсСкачать
Лекция 31.1. Кривые второго порядка. ЭллипсСкачать

#198. ЭЛЛИПС, ГИПЕРБОЛА, ПАРАБОЛАСкачать

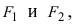
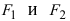
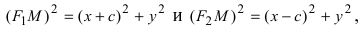
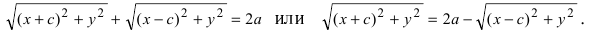
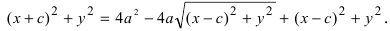
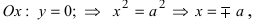 т.е. точками пересечения эллипса с осью абсцисс будут точки
т.е. точками пересечения эллипса с осью абсцисс будут точки 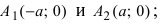
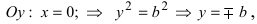 т.е. точками пересечения эллипса с осью ординат будут точки
т.е. точками пересечения эллипса с осью ординат будут точки 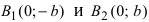 (Рис. 30).
(Рис. 30).