ТАНГЕНС (Tg α) острого угла в прямоугольном треугольнике равняется отношение противолежащего катета к прилежащему катету.
| α (радианы) | 0 | π/6 | π/4 | π/3 | π/2 | π | √3π/2 | 2π |
|---|---|---|---|---|---|---|---|---|
| α (градусы) | 0° | 30° | 45° | 60° | 90° | 180° | 270° | 360° |
| tg α (Тангенс) | 0 | 1/√3 | 1 | √3 | — | 0 | — | 0 |
| Угол в градусах | tg (Тангенс) |
|---|---|
| 0° | 0 |
| 1° | 0.0175 |
| 2° | 0.0349 |
| 3° | 0.0524 |
| 4° | 0.0699 |
| 5° | 0.0875 |
| 6° | 0.1051 |
| 7° | 0.1228 |
| 8° | 0.1405 |
| 9° | 0.1584 |
| 10° | 0.1763 |
| 11° | 0.1944 |
| 12° | 0.2126 |
| 13° | 0.2309 |
| 14° | 0.2493 |
| 15° | 0.2679 |
| 16° | 0.2867 |
| 17° | 0.3057 |
| 18° | 0.3249 |
| 19° | 0.3443 |
| 20° | 0.364 |
| 21° | 0.3839 |
| 22° | 0.404 |
| 23° | 0.4245 |
| 24° | 0.4452 |
| 25° | 0.4663 |
| 26° | 0.4877 |
| 27° | 0.5095 |
| 28° | 0.5317 |
| 29° | 0.5543 |
| 30° | 0.5774 |
| 31° | 0.6009 |
| 32° | 0.6249 |
| 33° | 0.6494 |
| 34° | 0.6745 |
| 35° | 0.7002 |
| 36° | 0.7265 |
| 37° | 0.7536 |
| 38° | 0.7813 |
| 39° | 0.8098 |
| 40° | 0.8391 |
| 41° | 0.8693 |
| 42° | 0.9004 |
| 43° | 0.9325 |
| 44° | 0.9657 |
| 45° | 1 |
| 46° | 1.0355 |
| 47° | 1.0724 |
| 48° | 1.1106 |
| 49° | 1.1504 |
| 50° | 1.1918 |
| 51° | 1.2349 |
| 52° | 1.2799 |
| 53° | 1.327 |
| 54° | 1.3764 |
| 55° | 1.4281 |
| 56° | 1.4826 |
| 57° | 1.5399 |
| 58° | 1.6003 |
| 59° | 1.6643 |
| 60° | 1.7321 |
| 61° | 1.804 |
| 62° | 1.8807 |
| 63° | 1.9626 |
| 64° | 2.0503 |
| 65° | 2.1445 |
| 66° | 2.246 |
| 67° | 2.3559 |
| 68° | 2.4751 |
| 69° | 2.6051 |
| 70° | 2.7475 |
| 71° | 2.9042 |
| 72° | 3.0777 |
| 73° | 3.2709 |
| 74° | 3.4874 |
| 75° | 3.7321 |
| 76° | 4.0108 |
| 77° | 4.3315 |
| 78° | 4.7046 |
| 79° | 5.1446 |
| 80° | 5.6713 |
| 81° | 6.3138 |
| 82° | 7.1154 |
| 83° | 8.1443 |
| 84° | 9.5144 |
| 85° | 11.4301 |
| 86° | 14.3007 |
| 87° | 19.0811 |
| 88° | 28.6363 |
| 89° | 57.29 |
| 90° | ∞ |
| Угол | tg (Тангенс) |
|---|---|
| 91° | -57.29 |
| 92° | -28.6363 |
| 93° | -19.0811 |
| 94° | -14.3007 |
| 95° | -11.4301 |
| 96° | -9.5144 |
| 97° | -8.1443 |
| 98° | -7.1154 |
| 99° | -6.3138 |
| 100° | -5.6713 |
| 101° | -5.1446 |
| 102° | -4.7046 |
| 103° | -4.3315 |
| 104° | -4.0108 |
| 105° | -3.7321 |
| 106° | -3.4874 |
| 107° | -3.2709 |
| 108° | -3.0777 |
| 109° | -2.9042 |
| 110° | -2.7475 |
| 111° | -2.6051 |
| 112° | -2.4751 |
| 113° | -2.3559 |
| 114° | -2.246 |
| 115° | -2.1445 |
| 116° | -2.0503 |
| 117° | -1.9626 |
| 118° | -1.8807 |
| 119° | -1.804 |
| 120° | -1.7321 |
| 121° | -1.6643 |
| 122° | -1.6003 |
| 123° | -1.5399 |
| 124° | -1.4826 |
| 125° | -1.4281 |
| 126° | -1.3764 |
| 127° | -1.327 |
| 128° | -1.2799 |
| 129° | -1.2349 |
| 130° | -1.1918 |
| 131° | -1.1504 |
| 132° | -1.1106 |
| 133° | -1.0724 |
| 134° | -1.0355 |
| 135° | -1 |
| 136° | -0.9657 |
| 137° | -0.9325 |
| 138° | -0.9004 |
| 139° | -0.8693 |
| 140° | -0.8391 |
| 141° | -0.8098 |
| 142° | -0.7813 |
| 143° | -0.7536 |
| 144° | -0.7265 |
| 145° | -0.7002 |
| 146° | -0.6745 |
| 147° | -0.6494 |
| 148° | -0.6249 |
| 149° | -0.6009 |
| 150° | -0.5774 |
| 151° | -0.5543 |
| 152° | -0.5317 |
| 153° | -0.5095 |
| 154° | -0.4877 |
| 155° | -0.4663 |
| 156° | -0.4452 |
| 157° | -0.4245 |
| 158° | -0.404 |
| 159° | -0.3839 |
| 160° | -0.364 |
| 161° | -0.3443 |
| 162° | -0.3249 |
| 163° | -0.3057 |
| 164° | -0.2867 |
| 165° | -0.2679 |
| 166° | -0.2493 |
| 167° | -0.2309 |
| 168° | -0.2126 |
| 169° | -0.1944 |
| 170° | -0.1763 |
| 171° | -0.1584 |
| 172° | -0.1405 |
| 173° | -0.1228 |
| 174° | -0.1051 |
| 175° | -0.0875 |
| 176° | -0.0699 |
| 177° | -0.0524 |
| 178° | -0.0349 |
| 179° | -0.0175 |
| 180° | 0 |
| Угол | tg (Тангенс) |
|---|---|
| 181° | 0.0175 |
| 182° | 0.0349 |
| 183° | 0.0524 |
| 184° | 0.0699 |
| 185° | 0.0875 |
| 186° | 0.1051 |
| 187° | 0.1228 |
| 188° | 0.1405 |
| 189° | 0.1584 |
| 190° | 0.1763 |
| 191° | 0.1944 |
| 192° | 0.2126 |
| 193° | 0.2309 |
| 194° | 0.2493 |
| 195° | 0.2679 |
| 196° | 0.2867 |
| 197° | 0.3057 |
| 198° | 0.3249 |
| 199° | 0.3443 |
| 200° | 0.364 |
| 201° | 0.3839 |
| 202° | 0.404 |
| 203° | 0.4245 |
| 204° | 0.4452 |
| 205° | 0.4663 |
| 206° | 0.4877 |
| 207° | 0.5095 |
| 208° | 0.5317 |
| 209° | 0.5543 |
| 210° | 0.5774 |
| 211° | 0.6009 |
| 212° | 0.6249 |
| 213° | 0.6494 |
| 214° | 0.6745 |
| 215° | 0.7002 |
| 216° | 0.7265 |
| 217° | 0.7536 |
| 218° | 0.7813 |
| 219° | 0.8098 |
| 220° | 0.8391 |
| 221° | 0.8693 |
| 222° | 0.9004 |
| 223° | 0.9325 |
| 224° | 0.9657 |
| 225° | 1 |
| 226° | 1.0355 |
| 227° | 1.0724 |
| 228° | 1.1106 |
| 229° | 1.1504 |
| 230° | 1.1918 |
| 231° | 1.2349 |
| 232° | 1.2799 |
| 233° | 1.327 |
| 234° | 1.3764 |
| 235° | 1.4281 |
| 236° | 1.4826 |
| 237° | 1.5399 |
| 238° | 1.6003 |
| 239° | 1.6643 |
| 240° | 1.7321 |
| 241° | 1.804 |
| 242° | 1.8807 |
| 243° | 1.9626 |
| 244° | 2.0503 |
| 245° | 2.1445 |
| 246° | 2.246 |
| 247° | 2.3559 |
| 248° | 2.4751 |
| 249° | 2.6051 |
| 250° | 2.7475 |
| 251° | 2.9042 |
| 252° | 3.0777 |
| 253° | 3.2709 |
| 254° | 3.4874 |
| 255° | 3.7321 |
| 256° | 4.0108 |
| 257° | 4.3315 |
| 258° | 4.7046 |
| 259° | 5.1446 |
| 260° | 5.6713 |
| 261° | 6.3138 |
| 262° | 7.1154 |
| 263° | 8.1443 |
| 264° | 9.5144 |
| 265° | 11.4301 |
| 266° | 14.3007 |
| 267° | 19.0811 |
| 268° | 28.6363 |
| 269° | 57.29 |
| 270° | ∞ |
| Угол | tg (Тангенс) |
|---|---|
| 271° | -57.29 |
| 272° | -28.6363 |
| 273° | -19.0811 |
| 274° | -14.3007 |
| 275° | -11.4301 |
| 276° | -9.5144 |
| 277° | -8.1443 |
| 278° | -7.1154 |
| 279° | -6.3138 |
| 280° | -5.6713 |
| 281° | -5.1446 |
| 282° | -4.7046 |
| 283° | -4.3315 |
| 284° | -4.0108 |
| 285° | -3.7321 |
| 286° | -3.4874 |
| 287° | -3.2709 |
| 288° | -3.0777 |
| 289° | -2.9042 |
| 290° | -2.7475 |
| 291° | -2.6051 |
| 292° | -2.4751 |
| 293° | -2.3559 |
| 294° | -2.246 |
| 295° | -2.1445 |
| 296° | -2.0503 |
| 297° | -1.9626 |
| 298° | -1.8807 |
| 299° | -1.804 |
| 300° | -1.7321 |
| 301° | -1.6643 |
| 302° | -1.6003 |
| 303° | -1.5399 |
| 304° | -1.4826 |
| 305° | -1.4281 |
| 306° | -1.3764 |
| 307° | -1.327 |
| 308° | -1.2799 |
| 309° | -1.2349 |
| 310° | -1.1918 |
| 311° | -1.1504 |
| 312° | -1.1106 |
| 313° | -1.0724 |
| 314° | -1.0355 |
| 315° | -1 |
| 316° | -0.9657 |
| 317° | -0.9325 |
| 318° | -0.9004 |
| 319° | -0.8693 |
| 320° | -0.8391 |
| 321° | -0.8098 |
| 322° | -0.7813 |
| 323° | -0.7536 |
| 324° | -0.7265 |
| 325° | -0.7002 |
| 326° | -0.6745 |
| 327° | -0.6494 |
| 328° | -0.6249 |
| 329° | -0.6009 |
| 330° | -0.5774 |
| 331° | -0.5543 |
| 332° | -0.5317 |
| 333° | -0.5095 |
| 334° | -0.4877 |
| 335° | -0.4663 |
| 336° | -0.4452 |
| 337° | -0.4245 |
| 338° | -0.404 |
| 339° | -0.3839 |
| 340° | -0.364 |
| 341° | -0.3443 |
| 342° | -0.3249 |
| 343° | -0.3057 |
| 344° | -0.2867 |
| 345° | -0.2679 |
| 346° | -0.2493 |
| 347° | -0.2309 |
| 348° | -0.2126 |
| 349° | -0.1944 |
| 350° | -0.1763 |
| 351° | -0.1584 |
| 352° | -0.1405 |
| 353° | -0.1228 |
| 354° | -0.1051 |
| 355° | -0.0875 |
| 356° | -0.0699 |
| 357° | -0.0524 |
| 358° | -0.0349 |
| 359° | -0.0175 |
| 360° | 0 |
Как распечатать таблицу? Левой кнопкой на компьютерной мишке выделите нужную часть таблицы, на выделенном фоне нажмите правую кнопку мишки и в появившемся меню перейдете в пункт «Печать».
Чему равен тангенс 30? …
— Ищем в таблице соответствующее значение. Правильный ответ: 0.5774
Видео:Как просто запомнить, что такое sin, cos, tg?! #косинус #синус #тангенс #математика #огэ #егэСкачать

Тригонометрическая таблица
В статье, мы полностью разберемся, как выглядит таблица тригонометрических значений, синуса, косинуса, тангенса и котангенса . Рассмотрим основное значение тригонометрических функций, от угла в 0,30,45,60,90. 360 градусов. И посмотрим как пользоваться данными таблицами в вычислении значения тригонометрических функций.
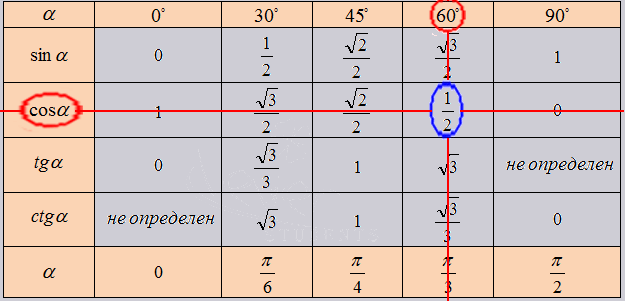
Первой рассмотрим таблицу косинуса, синуса, тангенса и котангенса от угла в 0, 30, 45, 60, 90. градусов. Определение данных величин дают определить значение функций углов в 0 и 90 градусов:
sin 0 0 =0, cos 0 0 = 1. tg 0 0 = 0, котангенс от 0 0 будет неопределенным
sin 90 0 = 1, cos 90 0 =0, ctg90 0 = 0,тангенс от 90 0 будет неопределенным
Если взять прямоугольные треугольники углы которых от 30 до 90 градусов. Получим:
sin 30 0 = 1/2, cos 30 0 = √3/2, tg 30 0 = √3/3, ctg 30 0 = √3
sin 45 0 = √2/2, cos 45 0 = √2/2, tg 45 0 = 1, ctg 45 0 = 1
sin 60 0 = √3/2, cos 60 0 = 1/2, tg 60 0 =√3 , ctg 60 0 = √3/3
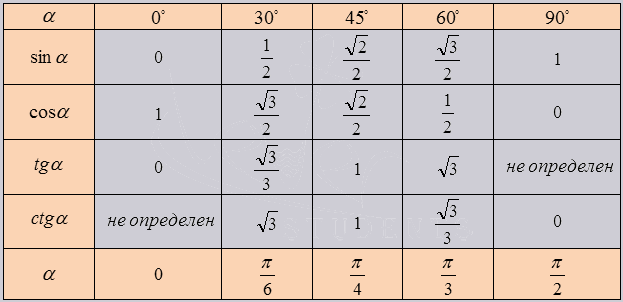
Изобразим все полученные значения в виде тригонометрической таблицы:
Видео:Алгебра 10 класс. 2 октября. Тангенс и котангенс на окружностиСкачать

Таблица синусов, косинусов, тангенсов и котангенсов!
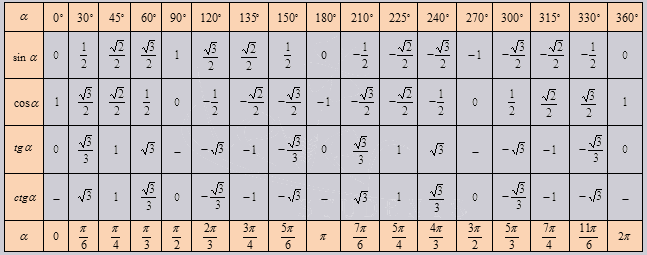
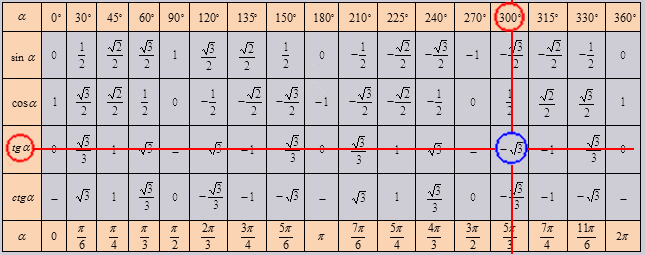
Если использовать формулу приведения, наша таблица увеличится, добавятся значения для углов до 360 градусов. Выглядеть она будет как:
Так же исходя из свойств периодичности таблицу можно увеличить, если заменим углы на 0 0 +360 0 *z . 330 0 +360 0 *z, в котором z является целым числом. В данной таблице возможно вычислить значение всех углов, соответствующими точками в единой окружности.
Разберем наглядно как использовать таблицу в решении.
Все очень прост. Так как нужное нам значение лежит в точке пересечения нужных нам ячеек. К примеру возьмем cos угла 60 градусов, в таблице это будет выглядеть как:
В итоговой таблице основных значений тригонометрических функций, действуем так же. Но в данной таблице возможно узнать сколько составит тангенс от угла в 1020 градусов, он = -√3 Проверим 1020 0 = 300 0 +360 0 *2. Найдем по таблице.
Для более поиска тригонометрических значений углов с точностью до минут используются таблицы Брадиса. Подробная инструкция как ими пользоваться на странице по ссылке.
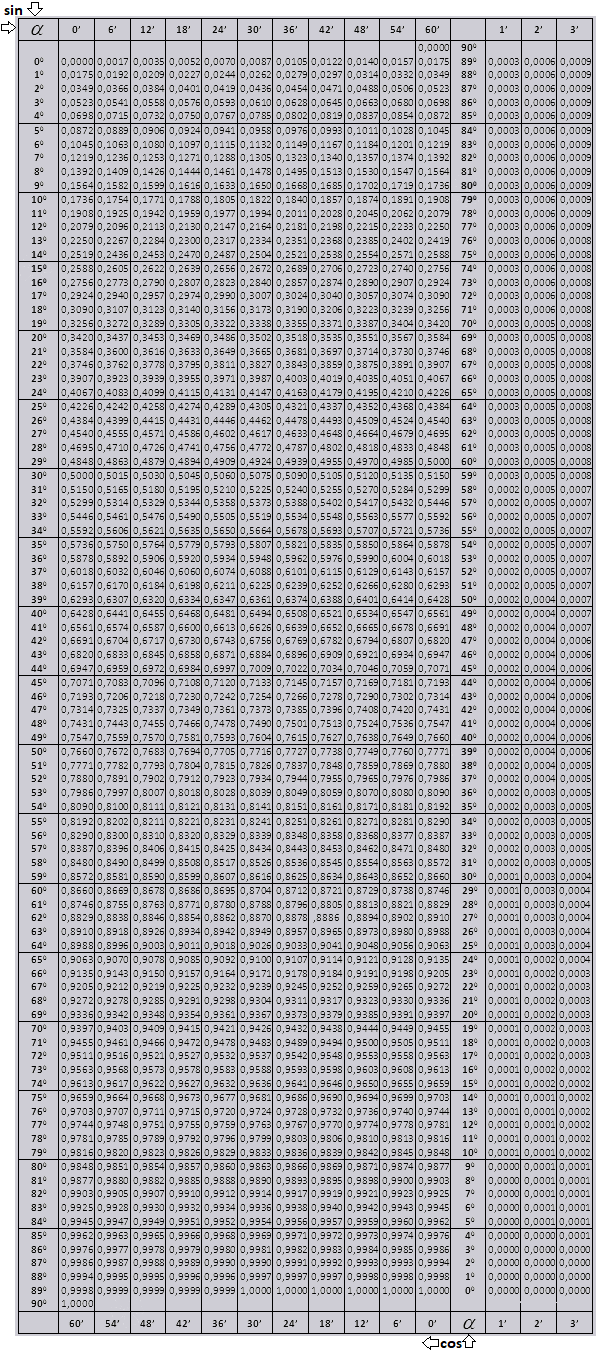
Таблица Брадиса. Для синуса, косинуса, тангенса и котангенса.
Таблицы Брадиса поделены на несколько частей, состоят из таблиц косинуса и синуса, тангенса и котангенса — которая поделена на две части (tg угла до 90 градусов и ctg малых углов).
Синус и косинус
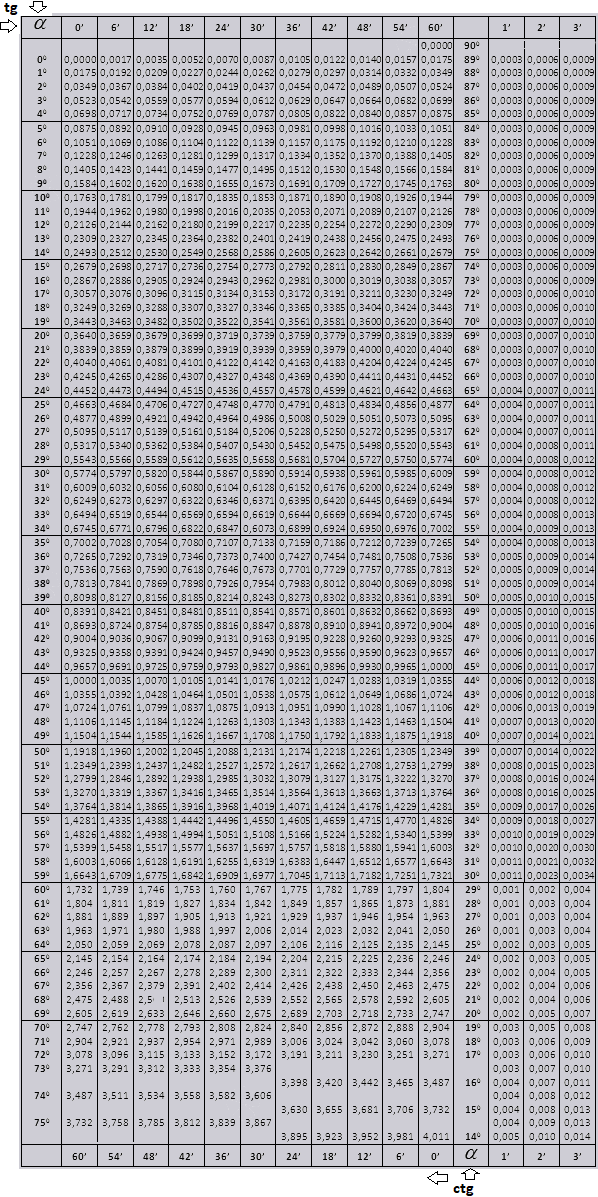
tg угла начиная с 0 0 заканчивая 76 0 , ctg угла начиная с 14 0 заканчивая 90 0 .
tg до 90 0 и ctg малых углов.
Разберемся как пользоваться таблицами Брадиса в решении задач.
Найдем обозначение sin (обозначение в столбце с левого края) 42 минут (обозначение находится на верхней строчке). Путем пересечения ищем обозначение, оно = 0,3040.

Величины минут указаны с промежутком в шесть минут, как быть если нужное нам значение попадет именно в этот промежуток. Возьмем 44 минуты, а в таблице есть только 42. Берем за основу 42 и воспользуемся добавочными столбцами в правой стороне, берем 2 поправку и добавляем к 0,3040 + 0,0006 получаем 0,3046.

При sin 47 мин, берем за основу 48 мин и отнимаем от нее 1 поправку, т.е 0,3057 — 0,0003 = 0,3054

При вычислении cos работаем аналогично sin только за основу берем нижнюю строку таблицы. К примеру cos 20 0 = 0.9397

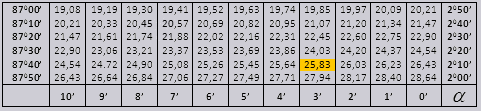
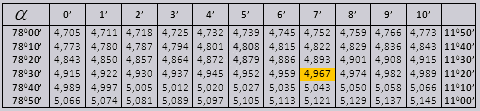
Значения tg угла до 90 0 и cot малого угла, верны и поправок в них нет. К примеру, найти tg 78 0 37мин = 4,967
а ctg 20 0 13мин = 25,83
Ну вот мы и рассмотрели основные тригонометрические таблицы. Надеемся это информация была для вас крайне полезной. Свои вопросы по таблицам, если они появились, обязательно пишите в комментариях!
Если материал был полезен, вы можете отправить донат или поделиться данным материалом в социальных сетях:
Видео:Синус, косинус, тангенс, котангенс за 5 МИНУТСкачать

Тема: Значения Sin, Cos и tg для углов 300, 450, 600
Тема: Значения Sin, Cos и tg для углов 300, 450, 600.
Цель: Создать условия для восприятия и осмысления темы «Значения Sin, Cos и tg для углов 300, 450, 600». Формировать умения решения прямоугольных треугольников, используя Sin, Cos и tg острого угла.
Способствовать развитию у учащихся интеллектуальных умений на уроке.
Прививать культуру умственного труда.
Оборудование: разноуровневые карточки, тесты, таблицы Брадиса, мультимедийный проектор
— Друзья мои, я очень рада
Войти в приветливый ваш класс.
И для меня уже награда,
Вниманье ваших умных глаз.
Я знаю, каждый в классе гений,
Но без труда, талант не впрок.
Скрестим же шпаги наших знаний
И вместе проведем урок.
II. Актуализация знаний учащихся.
а) Математический диктант.
Закончи предложение (проверка проводится с помощью мультимедийного проектора)
5 правильных ответов – «5»
4 правильных ответа – «4»
3 правильных ответа – «3»
1. Синусом острого угла прямоугольного треугольника называется отношение …
2. Косинусом острого угла прямоугольного треугольника называется отношение …
3. Тангенсом острого угла прямоугольного треугольника называется отношение …
4. Запишите формулой, чему равен тангенс угла α.
5. Запишите основное тригонометрическое тождество.
б) Устная работа по готовым чертежам ( в это время два ученика работают по карточкам на обратной стороне доски)

Sin α, Cos α, tg α
Sin β, Cos β, tg β,
если ∠C = 900, АВ=13, ВС=5
В С Найти: SABCD — ?
если АК=4, КД=5, ∠A=600.

Sin P, Cos P, tg P,
Sin N, Cos N, tg N,
М N если РМ=4, PN=5, NM=3
Найдите катеты прямоугольного треугольника, гипотенуза которого равна 2 см, один из острых углов равен 300.
Ученики класса проверяют задания по карточкам.
III. Изучение нового материала.
Умение находить значения тригонометрических функций острых углов требуется в различных областях человеческой деятельности. Так, при артиллерийской стрельбе стволами орудий придается некоторый угол возвышения, который учитывается при расчете дальности снаряда. При нахождении равнодействующей и составляющих сил во время движения тела по наклонной плоскости, при вращательном движении и т. д. также используется тригонометрические функции острых углов. В дальнейшем мы познакомимся с таблицами, по которым можно будет находить значение тригонометрических функций любого угла. На уроке мы вычислим значение тригонометрических функций углов 300, 450, 600. Эти значения полезно запомнить. Сейчас мы вместе решим несколько задач и результаты ответов занесем в таблицу.

Найти: Sin 450, Cos 450, tg 450
1.∠C=900, ∠A=450, значит ∠В=450, поэтому ∆ АВС – равнобедренный 2. ВС=АС=m, по теореме Пифагора АВ= √m2 +√m2 = √2m2=m√2
А катет говорит гипотенузе: «Навсегда
Сдружились мы с тобой навеки крепко
И ссориться не будем мы с тобою никогда,
Сковал нас Пифагор давно уж цепко»
3. Sin 450 = 










Найти: Sin 300, Cos 300, tg 300.
1.Т. к. ∠С=900 и ∠А=300, то ∠В=600; 2.пусть ВС=m, тогда АВ=2m; АС=√АВ2 — √ВС2 = √(2m)2 — √m2 = √4m2 – m2 = √3m2= m√3.
3.Sin 300 = 









— По аналогии самостоятельно найдите Sin 600, Cos 600, tg 600 в ∆ АВС, где ∠А=900, ∠В=600.
(проверить с помощью мультимедийного проектора)

Найти: Sin 600, Cos 600, tg 600.
1. Т. к. ∠А = 600, ∠С = 900, то ∠В = 300.
2. АС = m, AB = 2m, BC = m√3
3. Sin 600 = 







🌟 Видео
10 класс, 11 урок, Числовая окружностьСкачать

ЗНАЧЕНИЯ СИНУСА И КОСИНУСА НА ОКРУЖНОСТИСкачать

🔴 ТРИГОНОМЕТРИЯ С НУЛЯ (Тригонометрическая Окружность на ЕГЭ 2024 по математике)Скачать

Формулы приведения - как их легко выучить!Скачать

ТРИГОНОМЕТРИЯ | Синус, Косинус, Тангенс, КотангенсСкачать

Алгебра 10 класс Определение синуса, косинуса, тангенса угла ЛекцияСкачать

✓ Тригонометрия: с нуля и до ЕГЭ | #ТрушинLive #030 | Борис ТрушинСкачать

ТЕОРЕМА СИНУСОВ И ТЕОРЕМА КОСИНУСОВ. Тригонометрия | МатематикаСкачать

№1016. Вычислите синусы, косинусы и тангенсы углов 120°, 135°, 150°.Скачать

Решение тригонометрических уравнений. Подготовка к ЕГЭ | Математика TutorOnlineСкачать

Синус, косинус, тангенс и котангенс углов от 0 до 180 градусов.Скачать
Математика| Преобразование тригонометрических выражений. Формулы и задачиСкачать

ТРИГОНОМЕТРИЯ с нуля за 30 минутСкачать

Всё про углы в окружности. Геометрия | МатематикаСкачать

Что такое радиан?Скачать

Период тригонометрических функций тангенс и котангенс в градусах В какой четверти находится угол поСкачать

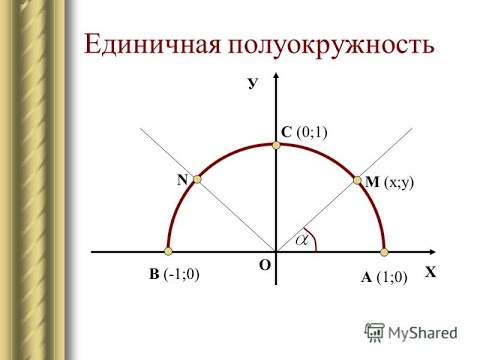
Единичная полуокружность. Синус и косинус угла от 0° до 180°Скачать