Пересечение и объединение треугольников (2 видео)

Основные геометрические фигуры

Содержание:

Содержание

Общие представления о геометрических фигурах. Объединение и пересечение фигур
Пример:
Изображение геометрических фигур
Точки и прямые
Взаимное расположение точек и прямых
Плоскости
Нахождение площади объединения треугольников. Метод вертикальной декомпозиции
Решение
Пересечение треугольников
Похожие презентации
🎥 Видео

Общие представления о геометрических фигурах. Объединение и пересечение фигур

На рисунках 2.1 и 2.2 изображены различные геометрические фигуры. Всякую геометрическую фигуру мы представляем себе составленной из точек.

Часть любой геометрической фигуры ТЭ.КЖ6 ЯВ-ляется геометрической фигурой.

Определение. Любое множество точек называют геометрической фигурой.

На рисунке 2.3 отрезок АВ есть часть прямой а, на рисунке 2.4 круг есть часть круга , на рисунке 2.5 шар вписан в куб и является частью куба.

Объединение нескольких фигур есть геометрическая фигура. На рисунке 2.6 фигура состоит из трех кругов, на рисунке 2.7 фигура состоит из треугольника и квадратов, на рисунке 2.8 фигура составлена из двух тетраэдров, на рисунке 2.9 фигура состоит из нескольких кубов. Объединение обозначается знаком .

Пересечение геометрических фигур есть также геометрическая фигура. На рисунке 2.10 отрезки АВ и CD пересекаются в точке Р. На рисунке 2.11 также отрезки MP и РК пересекаются в точке Р. Пересечением же отрезков ЕН и КХ на рисунке 2.12 является отрезок НК. Пересечение обозначается знаком .

Пример:

Рассмотрите возможные случаи взаимного расположения двух треугольников. В каждом случае назовите их пересечение.

Решение:

На рисунках 2.13—2.19 показано, что пересечение двух треугольников может:

а) не содержать точек (рис. 2.13);

б) состоять из одной точки (рис. 2.14);

в) быть отрезком (рис. 2.15);

г) быть треугольником (рис. 2.16);

д) быть четырехугольником (рис. 2.17);

е) быть пятиугольником (рис. 2.18);

ж) быть шестиугольником (рис. 2.19).

На рисунках 2.13—2.19 изображены различные случаи пересечения треугольников, если они лежат в одной плоскости. Однако, если треугольники лежат в разных плоскостях, то пересечением может быть:

а) точка (рис. 2.20);

б) отрезок (рис. 2.21, 2.22);

в) пустое множество точек (рис. 2.23).

Изображение геометрических фигур

Изображение плоских фигур на листе бумаги (или на доске) подчинено некоторым правилам и выполняется с использованием различных инструментов: линейки, угольника, транспортира, циркуля.

При изображении или построении плоских фигур мы не меняем формы и размеры тех фигур, которые изображаем. При этом сохраняются длины отрезков, величины углов, параллельность прямых и т. д. В геометрии говорят, что при этом получаются равные фигуры. Если нужно изобразить очень большие или очень маленькие фигуры, то сохраняются формы, а размеры могут быть изменены (в одном и том же отношении). При этом получают так называемые подобные фигуры.

Изображать пространственные фигуры на плоскости (листе бумаги) намного сложнее.

Наиболее важные из правил изображения пространственных фигур:

— все линии, которые не видны, которые закрыты гранями (плоскостями), изображаются пунктирными линиями;

— плоскости на рисунках изображаются иногда параллелограммами (рис. 2.24), а чаще — произвольной областью (рис. 2.25);

— длины отрезков сохраняются не всегда, но всегда середины отрезков изображаются серединами их изображения (это свойство означает, что если на модели у нас отмечена середина ребра, то и на рисунке будет обозначена тоже середина ребра);

— параллельные прямые (отрезки), имеющиеся на реальной модели, на рисунках тоже изображаются параллельными прямыми (отрезками).

Точки и прямые

Точки могут произвольно располагаться в пространстве: лежать и не лежать на плоскости (на рис. 2.26 точки А и Б лежат на плоскости, а точка С не лежит), принадлежать различным фигурам и не принадлежать им (на рис. 2.27 точка А принадлежит шару, а на рис. 2.28 не принадлежит ему).

Точки обозначаются прописными (заглавными) латинскими буквами: А, В, С, D, К, М, . .

Пусть даны две точки А и В. Проведем через точки А л В прямую (рис. 2.29). У нас появляется еще одно, важное понятие геометрии — прямая, которая также состоит из точек.

Изобразить прямую целиком невозможно, мы лишь условно изображаем ее часть (рис. 2.29).

Некоторые важные проблемы в геометрии решают путем введения законов — аксиом, которые принимаются без доказательства.

Слово «аксиома» в переводе с греческого языка означает «бесспорная истина, не требующая доказательств», т. е. очевидный факт, ясный сам по себе.

Аксиома 1.

Через любые две точки можно провести прямую, и только одну.

Прямые обозначаются строчными латинскими буквами: и т. д., а также соответствующими точками, лежащими на ней. Например, прямую на рисунке 2.29 можно обозначить АВ.

Взаимное расположение точек и прямых

Точки и прямые могут по-разному располагаться по отношению друг к другу (рис. 2.30).

Про точки М и К говорят, что они лежат на прямой , или что точки М и К принадлежат прямой . Точки А и В не лежат на прямой или не принадлежат прямой а.

Про прямую иногда говорят, что она проходит через точки. Так, прямая на рисунке 2.30 проходит через точки М, К. Можно также сказать, что прямая не проходит через точку А.

В курсе геометрии применяются некоторые удобные знаки, которые относятся к так называемой теории множеств: знак принадлежности и знак непринадлежности .

Запись читается: точка С принадлежит прямой р. Глядя на рисунок 2.30, можно записать:

Запись читается: точка D не принадлежит прямой р. Глядя на рисунок 2.30 можно записать:

Плоскости

Плоскости расположены в пространстве, в пространстве есть бесконечно много различных плоскостей. На рисунке 2.31 изображены несколько плоскостей, пересекающихся по одной прямой, а на рисунке 2.32 — параллельные друг другу плоскости.

Плоскости обозначаются строчными греческими буквами: . .

На рисунке 2.33 изображены плоскость , прямые и точки А, В и С. Про точку А и прямую говорят, что они лежат в плоскости или принадлежат ей. Про точки Б и С и прямую говорят, что они не лежат в плоскости или не принадлежат ей.

Принадлежность прямой плоскости обозначают знаком — включение, который показывает, что некоторое множество точек принадлежит другому множеству точек, например:

— точка А принадлежит плоскости ; — точка Б не лежит в плоскости ;

— прямая принадлежит плоскости ; — прямая не принадлежит плоскости .

Одно из свойств взаимного расположения прямой и плоскости формулируется как аксиома — аксиома прямой и плоскости.

Аксиома 2.

Прямая, проходящая через две точки плоскости, принадлежит этой плоскости. (Аксиома прямой и плоскости.)

Аксиома 3.

Через три точки, не лежащие на одной прямой, проходит одна и только одна плоскость. (Аксиома плоскости.)

Теорема 1. Через прямую и не лежащую на ней точку проходит одна, и только одна плоскость.

Любая прямая разбивает плоскость на два непустых множества (рис. 2.34). Объединение прямой с одним из образовавшихся множеств называется полуплоскостью. Прямую называют границей полуплоскости. На рисунке 2.34 прямая одновременно является границей обеих полуплоскостей.

Плоскость разбивает пространство на два множества, которые на рисунке 2.35 заштрихованы. Объединение этой плоскости с одним из образовавшихся множеств и называется полупространством. Плоскость называется границей полупространства. Из рисунка 2.35 ясно, что плоскость определяет сразу два полупространства.

Эта лекция взята со страницы полного курса лекций по изучению предмета «Математика»:

Смотрите также дополнительные лекции по предмету «Математика»:

Видео:Пересечение множеств. Объединение множеств. 5 класс.Скачать

Нахождение площади объединения треугольников. Метод вертикальной декомпозиции

Даны N треугольников. Требуется найти площадь их объединения.

Видео:Пересечение двух плоскостей. Плоскости в виде треугольникаСкачать

Решение

Здесь мы рассмотрим метод вертикальной декомпозиции, который в задачах на геометрию часто оказывается очень важным.

Итак, у нас имеется N треугольников, которые могут как угодно пересекаться друг с другом. Избавимся от этих пересечений с помощью вертикальной декомпозиции: найдём все точки пересечения всех отрезков (образующих треугольники), и отсортируем найденные точки по их абсциссе. Пусть мы получили некоторый массив B. Будем двигаться по этому массиву. На i-ом шаге рассматриваем элементы B[i] и B[i+1]. Мы имеем вертикальную полосу между прямыми X = B[i] и X = B[i+1], причём, согласно самому построению массива B, внутри этой полосы отрезки никак не пересекаются друг с другом. Следовательно, внутри этой полосы треугольники обрезаются до трапеций, причём стороны этих трапеций внутри полосы не пересекаются вообще. Будем двигаться по сторонам этих трапеций снизу вверх, и складывать площади трапеций, следя за тем, чтобы каждый кусок был учитан ровно один раз. Фактически, этот процесс очень напоминает обработку вложенных скобок. Сложив площади трапеций внутри каждой полосы, и сложив результаты для всех полос, мы и найдём ответ — площадь объединения треугольников.

Рассмотрим ещё раз процесс сложения площадей трапеций, уже с точки зрения реализации. Мы перебираем все стороны всех треугольников, и если какая-то сторона (не вертикальная, нам вертикальные стороны не нужны, и даже наоборот, будут сильно мешать) попадает в эту вертикальную полосу (полностью или частично), то мы кладём эту сторону в некоторый вектор, удобнее всего это делать в таком виде: координаты Y в точках пересечения стороны с границами вертикальной полосы, и номер треугольника. После того, как мы построили этот вектор, содержащий куски сторон, сортируем его по значению Y: сначала по левой Y, потом по правой Y. В результате первый в векторе элемент будет содержать нижнюю сторону самой нижней трапеции. Теперь мы просто идём по полученному вектору. Пусть i — текущий элемент; это означает, что i-ый кусок — это нижняя сторона некоторой трапеции, некоторого блока (который может содержать несколько трапеций), площадь которого мы хотим сразу прибавить к ответу. Поэтому мы устанавливаем некий счётчик треугольников равным 1, и поднимаемся по отрезкам вверх, и увеличиваем счётчик, если мы встречаем сторону какого-то треугольника в первый раз, и уменьшаем счётчик, если мы встречаем треугольник во второй раз. Если на каком-то отрезке j счётчик стал равным нулю, то мы нашли верхнюю границу блока — на этом мы останавливаемся, прибавляем площадь трапеции, ограниченной отрезками i и j, и i присваиваем j+1, и повторяем весь процесс заново.

Итак, благодаря методу вертикальной декомпозиции мы решили эту задачу, из геометрических примитивов использовав только пересечение двух отрезков.

Видео:Пересечение и объединение множеств. Алгебра, 8 классСкачать

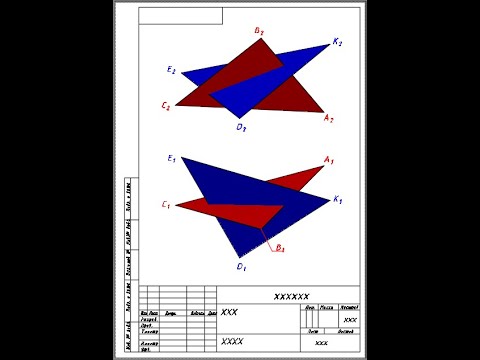
Пересечение треугольников

Точка >>

Пересечение треугольников. Какие фигуры могут быть получены при пересечении двух треугольников?

Слайд 11 из презентации «Пересечение множеств»

Размеры: 720 х 540 пикселей, формат: .jpg. Чтобы бесплатно скачать слайд для использования на уроке, щёлкните на изображении правой кнопкой мышки и нажмите «Сохранить изображение как. ». Скачать всю презентацию «Пересечение множеств.ppt» можно в zip-архиве размером 1571 КБ.

Видео:Алгебра 8 класс (Урок№39 - Пересечение и объединение множеств.)Скачать