Выберете верные утверждения чтобы четырехугольник можно было вписать

Геометрия | 5 — 9 классы

Выберите верные утверждения : А)чтобы четырёхугольник можно было вписать в окружность, необходимо, чтобы суммы его противоположных углов были равны 180 градусов Б)чтобы четырёхугольник можно было описать около окружности, необходимо, чтобы суммы длин его противоположных сторон были равны В) только равнобедренную трапецию можно вписать в окружность Г)не всякий треугольник можно описать около окружности.

Верные утверждения : А) Четырехугольник можно вписать в окружность тогда и только тогда, когда суммы его противоположных углов равны 180.

Б). Четырехугольник можно описать вокруг окружности тогда и только тогда, когда суммы длин его противоположных сторон равны.

Видео:Вписанные четырехугольники. 9 класс.Скачать

Укажите в ответе номера верных утверждений?

Укажите в ответе номера верных утверждений.

1) Около любого квадрата можно описать окружность 2) Сумма двух противоположных углов вписанного в окружность четырёхугольника равна 90% 3) Если диагонали параллелограмма делят его углы пополам, то этот параллелограмм — ромб.

Видео:Вписанные и описанные четырехугольники. Практическая часть. 9 класс.Скачать

Сторона правильного треугольника вписанного в некоторую окружность равна 4 / корень из 3?

Сторона правильного треугольника вписанного в некоторую окружность равна 4 / корень из 3.

Найдите сторону правельного четырёхугольника описанного около этой окружности.

Видео:19 задание огэ математика 2023 ВСЕ ТИПЫ геометрияСкачать

Докажите, что если около четырехугольника можно описать окружность, то сумма его противоположных углов равна 180 градусам?

Докажите, что если около четырехугольника можно описать окружность, то сумма его противоположных углов равна 180 градусам.

Видео:Свойство и признак вписанного четырехугольникаСкачать

Докажите, что у четырёхугольника, описанного около окружности, суммы противолежащих сторон равны?

Докажите, что у четырёхугольника, описанного около окружности, суммы противолежащих сторон равны.

Видео:11 класс, 44 урок, Описанный четырехугольникСкачать

Если сумма двух противоположных углов четырехугольника равна 90 градусов, около этого четырехугольника можно описать окружность?

Если сумма двух противоположных углов четырехугольника равна 90 градусов, около этого четырехугольника можно описать окружность?

Видео:3 правила для вписанного четырехугольника #shortsСкачать

Сумма двух противоположных сторон описанного четырёхугольника и радиус вписанной в него окружности соответственно равны 24 и 5?

Сумма двух противоположных сторон описанного четырёхугольника и радиус вписанной в него окружности соответственно равны 24 и 5.

Найдите площадь четырёхугольника.

Видео:Описанная и вписанная окружности четырехугольника - 8 класс геометрияСкачать

Дана равнобедренная трапеция, в которую вписана окружность и около которой описана окружность?

Дана равнобедренная трапеция, в которую вписана окружность и около которой описана окружность.

Отношение длины описанной окружности к длине вписанной окружности равно 2‍√5.

‍ Найдите углы трапеции.

Видео:Четырехугольники, вписанные в окружность. 9 класс.Скачать

Сторона правильного четырёхугольника, вписанного в окружность, равна 2?

Сторона правильного четырёхугольника, вписанного в окружность, равна 2.

Найдите сторону правильного треугольника, описанного около этой же окружности.

Видео:Вписанный в окружность четырёхугольник.Скачать

Какие из следующих утверждений верны?

Какие из следующих утверждений верны?

1. Если радиус окружности равен 7, а расстояние от центра окружности до прямой равно 5, то эти прямая и окружность не имеют общих точек.

2. Сумма двух противоположных углов четырёхугольника равна 180.

3. Центр окружности, описанной около прямоугольного треугольника, лежит на стороне этого треугольника.

Видео:Вписанный четырёхугольник | ЕГЭ-2018. Задание 16. Математика. Профильный уровень | Борис ТрушинСкачать

Нужно решение?

Дана равнобедренная трапеция, в которую вписана окружность и около которой описана окружность.

Отношение длины описанной окружности к длине вписанной окружности равно 2‍√5.

‍ Найдите углы трапеции.

На этой странице находится вопрос Выберите верные утверждения : А)чтобы четырёхугольник можно было вписать в окружность, необходимо, чтобы суммы его противоположных углов были равны 180 градусов Б)чтобы четырёхугольник можно было опис?. Здесь же – ответы на него, и похожие вопросы в категории Геометрия, которые можно найти с помощью простой в использовании поисковой системы. Уровень сложности вопроса соответствует уровню подготовки учащихся 5 — 9 классов. В комментариях, оставленных ниже, ознакомьтесь с вариантами ответов посетителей страницы. С ними можно обсудить тему вопроса в режиме on-line. Если ни один из предложенных ответов не устраивает, сформулируйте новый вопрос в поисковой строке, расположенной вверху, и нажмите кнопку.

15″ = 10″ + х» х» = 15″ — 10″ х = 5 S = 1 / 2 высоты * на сторону, к которой она проведена S = 1 / 2 * 5 * 10 S = 25 см2 » — квадрат ( 15″ — 15 в квадрате).

Дано : АВС , АВ = ВС = 15 см АС = 10Найти : S — ? Решение : Высота, опущенная из вершины равнобедренного треугольника на его основание является одновременно и высотой, и медианой. ВН — высотаАН = НС = 5 смТреугольник АВН — прямоугольный, катет АН =..

Только если в общем виде , если будет. Дан угол прорстро получать и посчитай.

Ииосноваа Х сотая ле врмпо флтсяаходции аходции адь трапплощадей.

DOA по двум углам (накрест лежащим) , BO : OD = OC : AO = BC : AD = 2 : 3 2AO = 3OC AO + OC = 20 2AO + 2OC = 40 5OC = 40 OC = 8 AO = 12.

OB = OA, OC = CO(общая сторона), AC = BC.

1)тр. АОС = тр. ОСВ (по двум катетам) = > АС = ВС(соотв. Элементы).

Держи . Вроде так правильно.

10 дм — 100 см. Провоим высоту, она делит оснеование на две равные части, значит кусочек в равнобедренном треугольнике равен 6. По теореме пифагора находим высоту. Она равна 8. Площадь равна полупроизведение основания на высоту. 12 * 8 и делим н..

Видео:ФИЗИКА ЕГЭ 2024 ВАРИАНТ 16 ДЕМИДОВА РАЗБОР ЗАДАНИЙ I Эмиль Исмаилов - Global_EEСкачать

Можно ли вписать четырёхугольник в окружность? Когда можно вписать?

Содержание:

Почти в любой четырехугольник можно вписать окружность. Трапеция, прямоугольник и квадрат для этого подходят всегда, тогда как сложные геометрические фигуры с четырьмя углами вписываются в круг избирательно. Рассмотрим условия, при которых 4-угольник может касаться точек на окружности всеми вершинами.

Видео:Разбор 7 варианта из сборника Рохлова 2024Скачать

Вписанный

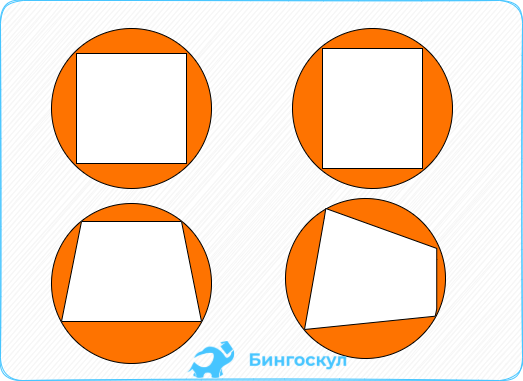
Вписанной называется фигура, вершины которой располагаются на окружности. Все треугольники и правильные 4-угольники, вроде квадрата и прямоугольника, размещаются внутри круга, причём их вершины совмещаются с точками на окружности. Вокруг неправильной фигуры с четырьмя углами не всегда можно описать круг. Разбираемся, какие условия нужно выполнить для решения проблемы.

У квадрата и прямоугольника все углы прямые – равны 90°, но это не ключ к разгадке. Случай с параллелограммом тому подтверждение. Чем примечательны прямоугольные 4-угольники? Может дело в сумме углов?

Трапеция в круг вписывается, но только равнобедренная. Одно из её свойств – сумма внутренних углов равна 360°, а соседних – 180°. Получается, что четырехугольник можно вписать в окружность, если сумма противоположных углов равняется 180°. Проверим на практике.

Помните: правило применимо только для выпуклых фигур, расположенных по одну сторону от проходящих через все стороны прямых.

Выпуклый дельтоид вписывается в круг, когда имеет пару прямых углов – называется прямоугольным.

Задача

Известны величины двух соседних углов вписанного четырёхугольника: 65° и 83°. Вычислить размеры сразу большего, затем – меньшего из оставшихся.

Известно, что сумма противоположных углов указанной геометрической фигуры равняется 180°. Отнимем от значения сначала большую цифру, затем – меньшую, чтобы выполнить условия задачи – найти неизвестные значения в указанном порядке.

180 – 65 = 115° – больший угол, 180 – 83 = 97° – меньший.

Видео:Урок 2. Описанная окружность около четырехугольника. Задача из ОГЭ| Подобные треугольникиСкачать

В какой четырехугольник можно вписать окружность

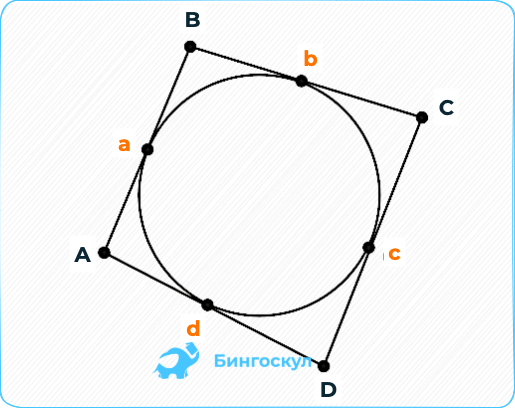
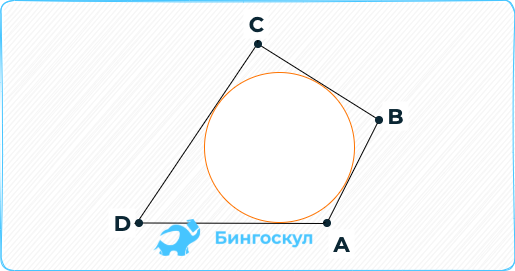
Описанным называют 4-угольник, стороны которого касаются круга. Существует теорема, показывающая, когда в четырехугольник можно вписать окружность: сумма его противоположных сторон должна быть одинаковой: AB + CD = BC + AD. В случае с прямоугольником условие не выполняется.

Правило работает для дельтоида, квадрата и даже неправильного выпуклого 4-угольника, подпадающего под теорему.

В параллелограмм вписывается круг в случае, если он является ромбом.

Задача

Стороны описанной фигуры относятся как 1:2:3. Найти длину четвёртой, если периметр равняется 32 см.

Составим уравнение. Зная, что суммы противоположных сторон 4-угольника равны:

Периметр равняется суме сторон: P = AB + ВС + AD + BC либо x + 2x + 2x + 3x = 32.

Видео:Стереометрия 10 класс. Часть 1 | МатематикаСкачать

Выберете верные утверждения чтобы четырехугольник можно было вписать

Укажите номера неверных утверждений. Выберите 2 варианта из списка.

1) В равнобедренном треугольнике все углы равны.

2) Во всякий четырёхугольник можно вписать окружность.

3) Диагональ параллелограмма делит его на два равных треугольника.

4) Все точки каждой из двух параллельных прямых равноудалены от другой прямой.

1) Неверно. В равнобедренном треугольнике углы при основании равны.

2) Неверно. Во всякий выпуклый четырёхугольник можно вписать окружность.

3) Верно. Так как стороны параллелограмма попарно равны.

4) Верно. Ответ: 12
2 1 7 7 4 5 1

🎬 Видео

ОГЭ по математике. Площадь четырехугольника можно вычислить по формуле (вар. 5)Скачать

ЕГЭ Физика 2024 Демидова (ФИПИ) 30 типовых вариантов, вариант 4, подробный разбор всех заданийСкачать

ЕГЭ Физика 2024 Демидова (ФИПИ) 30 типовых вариантов, вариант 3, подробный разбор всех заданийСкачать

ОГЭ по математике. Площадь четырехугольника можно вычислить (вар. 4)Скачать

Тема 9. Вписанные и описанные четырехугольникиСкачать

ЕГЭ Физика 2024 Демидова (ФИПИ) 30 типовых вариантов, вариант 7, подробный разбор всех заданийСкачать