Вписанный и описанный в окружность восьмиугольник

Видео:Вписанные и описанные четырехугольники. Практическая часть. 9 класс.Скачать

Восьмиугольник, виды, свойства и формулы

Видео:Вписанные и описанные окружности. Вебинар | МатематикаСкачать

Формулы расчёта параметров правильного восьмиугольника

• t — длина стороны восьмиугольника
• r — радиус вписанной окружности
• R — радиус описанной окружности
• S — площадь восьмиугольника
• k — константа, равная (1+2) >)> ≈ 2,414213562373095

Так как правильный восьмиугольник можно получить соответствующим отсечением углов квадрата со стороной kt , радиус вписанной окружности, радиус описанной окружности и площадь правильного восьмиугольника можно вычислить и без использования тригонометрических функций:

Радиус вписанной окружности правильного восьмиугольника:

Радиус описанной окружности правильного восьмиугольника:

Площадь правильного восьмиугольника:

Через сторону восьмиугольника

Через радиус описанной окружности

Через апофему (высоту)

Видео:Вписанная и описанная окружность - от bezbotvyСкачать

Правильный восьмиугольник (понятие и определение):

Правильный восьмиугольник (октагон) – это правильный многоугольник с восемью сторонами.

В свою очередь правильный многоугольник – это многоугольник, у которого все стороны и углы одинаковые.

Правильный восьмиугольник – это восьмиугольник, у которого все стороны равны, а все внутренние углы равны 135°.

Рис. 3. Правильный восьмиугольник

Правильный восьмиугольник имеет 8 сторон, 8 углов и 8 вершин.

Углы правильного восьмиугольника образуют восемь равнобедренных треугольников.

Правильный восьмиугольник можно построить с помощью циркуля и линейки: проведя к сторонам квадрата серединные перпендикуляры и соединив точки их пересечения с описанной окружностью квадрата с его сторонами.

Видео:Построение 8 угольника циркулемСкачать

Литература

• Pierre Wantzel. Recherches sur les moyens de Reconnaître si un Problème de géométrie peau se résoudre avec la règle et le compas // Journal de Mathématiques. — 1837. — С. 366–372.
• W. W. Rose Ball, H. S. M.Coxeter. Mathematical recreations and Essays. — Thirteenth edition. — New York: The MacMillan company, 1947. — С. 141.

Перевод: Математические эссе и развлечения / перевод Н.И. Плужниковой, А.С.Попова, Г.М. Цукерман, под редакцией И.М.Яглома. — Москва: «Мир», 1986. — С. 156.

Видео:Вписанная и описанная окружности | Лайфхак для запоминанияСкачать

Применение восьмиугольников

Дорожный знак «Движение без остановки запрещено»

Восьмиугольный план Купола Скалы

В странах, принявших Венскую конвенцию о дорожных знаках и сигналах (в том числе в России), а также во многих других странах, знак «Движение без остановки запрещено» имеет вид красного восьмиугольника.

Восьмиугольные формы часто используются в архитектуре. Купол Скалы имеет восьмиугольный план. Башня Ветров в Афинах — ещё один пример восьмиугольной структуры. Восьмиугольный план встречается также в архитектуре церквей, таких как Собор Святого Георгия (Аддис-Абеба), Сан-Витале (в городе Равенна, Италия), Замок Кастель-дель-Монте (Апулия, Италия), Флорентийский баптистерий и . Центральное пространство в Ахенский собор, Капелла Карла Великого имеют планы в виде правильного восьмиугольника.

Видео:Окружность вписанная в треугольник и описанная около треугольника.Скачать

Построение

Точное построение

Проводим большую окружность k₁ (будущую описанную окружность семнадцатиугольника) с центром O.
Проводим её диаметр AB.
Строим к нему перпендикуляр m, пересекающий k₁ в точках C и D.
Отмечаем точку E — середину DO.
Посередине EO отмечаем точку F и проводим отрезок FA.
Строим биссектрису w₁ угла ∠OFA.
Строим w₂ — биссектрису угла между m и w₁, которая пересекает AB в точке G.
Проводим s — перпендикуляр к w₂ из точки F.
Строим w₃ — биссектрису угла между s и w₂. Она пересекает AB в точке H.
Строим окружность Фалеса (k₂) на диаметре HA. Она пересекается с CD в точках J и K.
Проводим окружность k₃ с центром G через точки J и K. Она пересекается с AB в точках L и N

Здесь важно не перепутать N с M, они расположены очень близко.
Строим касательную к k₃ через N.

Точки пересечения этой касательной с исходной окружностью k₁ — это точки P₃ и P₁₄ искомого семнадцатиугольника. Если принять середину получившейся дуги за P₀ и отложить дугу P₀P₁₄ по окружности три раза, все вершины семнадцатиугольника будут построены.

Примерное построение

Следующее построение хоть и приблизительно, но гораздо более удобно.

1. Ставим на плоскости точку M, строим вокруг неё окружность k и проводим её диаметр AB;
2. Делим пополам радиус AM три раза по очереди по направлению к центру (точки C, D и E).
3. Делим пополам отрезок EB (точка F).
4. строим перпендикуляр к AB в точке F.

Вкратце: строим перпендикуляр к диаметру на расстоянии 9/16 диаметра от B.

Точки пересечения последнего перпендикуляра с окружностью являются хорошим приближением для точек P₃ и P₁₄.

При этом построении получается относительная ошибка в 0,83%. Углы и стороны получаются таким образом немного больше, чем нужно. При радиусе 332,4 мм сторона получается длиннее на 1 мм.

Видео:Правильные многоугольники. Геометрия 9 класс | Математика | TutorOnlineСкачать

Признаки и свойства

Не всегда получается верно идентифицировать пятиугольник. Для этого математики предлагают признаки, которые применимы только к правильной фигуре. К ним можно отнести следующие:

Стороны равны между собой.
Любой угол правильного пятиугольника равен остальным его углам.

Следует отметить, что признаки справедливы для любого правильного многогранника. Пять осей симметрии имеет правильный пятиугольник (сколько сторон, столько и осей). Пентагон обладает некоторыми свойствами, которые будут очень полезны при решении задач. К ним можно отнести следующие:

Равенство сторон.
Углы равны по 108 градусов.
Центры вписанной и описанной окружностей совпадают.
Сумма внутренних углов равна 180 * (5 – 2) = 540 (градусов), а внешних – 360.
Количество диагоналей соответствует 5.
Значение площади кольца, которое образуется между вписанным и описанным кругами, эквивалентно произведению квадрата длины стороны на константу Pi / 4.
Биссектрисы, проведенные через центр, равны.
Диагонали — трисектрисы внутренних углов. Одна диагональ делит его на 1/3 и 2/3 части.
Отношение диагонали к стороне эквивалентно «золотому сечению» и равно [1 + 5^(1/2)] / 2.

Видео:Построить описанную окружность (Задача 1)Скачать

Другие восемнадцатиугольники фигуры

Звёздчатые 18 -угольники имеют символы >. Существует два правильных звёздчатых многоугольника: 185 > и >. Они используют те же самые вершины, но соединяют каждую пятую или седьмую вершину. Имеются также составные восемнадцатиугольники: > эквивалентен 2 > (двум девятиугольникам), > эквивалентен 3 > (трём шестиугольникам), > и > эквивалентны 2 > и 2 > (двум эннеаграммам), > эквивалентен 6 > (6 равносторонним треугольникам), и, наконец, > эквивалентен 9 > (девять двуугольников).

Видео:Геометрия - Построение восьмиугольникаСкачать

Как начертить восьмиугольник с помощью циркуля

Деление окружности на равные части и по­строение правильных вписанных многоуголь­ников можно выполнить как циркулем, так и с помощью угольников и рейсшины.

Деление окружности на четыре равные части и построение пра­вильного вписанного четырех­угольника. Две взаимно перпендикулярные центровые линии делят окружность на четыре равные части (рис. 115, а). Соединив точки пе­ресечения этих линий с окружностью прямы­ми, получают правильный вписанный четырех­угольник.

Деление окружности на восемь равных частей и построение пра­вильного вписанного восьмиуголь­ника. Две взаимно перпендикулярные линии, проведенные под углом 45° к центровым ли­ниям с помощью угольника с углами 45, 45 и 90° и рейсшины (рис. 115, б), вместе с центро­выми линиями разделят окружность на восемь равных частей.

Деление окружности на восемь равных час­тей можно выполнить циркулем. Для этого из точек 1 и 3 (точки пересечения центровых линий с окружностью) произвольным радиусом делаются засечки до взаимного пересечения, тем же радиусом делают две засечки из точек 3 и 5 (рис. 115, в). Через точки пересечения засечек и центр окружности проводят прямые линии до пересечения с окружностью в точках 2, 4, 6, 8.

Если полученные восемь точек соединить последовательно прямыми линиями, то полу­чится правильный вписанный восьмиугольник (рис. 115, в).

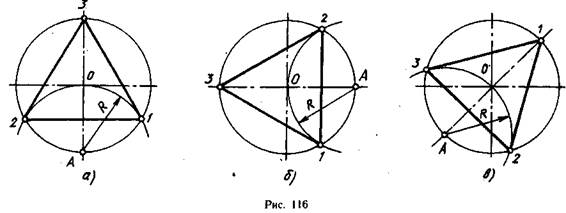
Деление окружности на три рав­ные части и построение правиль­ного вписанного треугольника вы­полняют с помощью циркуля или угольника с углами 30, 60 и 90° и рейсшины.

При делении окружности циркулем на три равные части из любой точки окружности, на­пример из точки Л пересечения центровых ли­ний с окружностью (рис. 116, а и б), проводят дугу радиусом R, равным радиусу данной ок­ружности, получают точки 1 и 2. Третья точка деления (точка 3) будет находиться на про­тивоположном конце диаметра, проходящего через точку Л. Последовательно соединив точ­ки 1, 2 и 3, получают правильный вписанный треугольник. При построении правильного впи­санного треугольника, если задана одна из его вершин, например точка 1, находят точку А. Для этого через заданную точку 1 проводят диаметр (рис. 116, в). Точка А будет находить­ся на противоположном конце этого диаметра. Затем проводят дугу радиусом R равным ра­диусу данной окружности, получают точки 2 и 3.

При делении окружности на три равные час­ти с помощью угольника и рейсшины через точку 1 под углом 60° проводят две прямые линии до пересечения с окружностью в точках 2 и 3 (рис. 117, а, б), точки 2 и 3 соединяют и получают правильный вписанный треугольник (рис. 117, в).

Деление окружности на шесть равных частей и построение пра­вильного вписанного шестиуголь­ника выполняют с помощью угольника с уг­лами 30, 60 и 90° и рейсшины или циркуля. При делении окружности на шесть равных частей циркулем из двух концов одного диа­метра радиусом, равным радиусу данной окруж­ности, проводят дуги до пересечения с окруж­ностью в точках 2, 6 и 3, 5 (рис. 118). Последовательно соединив полученные точки, полу­чают правильный вписанный шестиугольник. Деление окружности на шесть равных час-1ен и построение правильного вписанного шестиугольника с помощью угольника и рейс­шины показано на рис. 119 и 120. Деление окружности на двенад­цать равных частей и построение правильного вписанного двенад­цатиугольника выполняют с помощью угольника с углами 30, 60 и 90° и рейсшины или циркуля.

При делении окружности циркулем из четы­рех концов двух взаимно перпендикулярных диаметров окружности проводят радиусом, рав­ным радиусу данной окружности, дуги до пере­сечения с окружностью (рис. 121). Соединив по­лученные точки, получают двенадцатиугольник.

При построении двенадцатиугольника с по­мощью угольника и рейсшины точки деления строят, как показано на рис. 119 и 120.

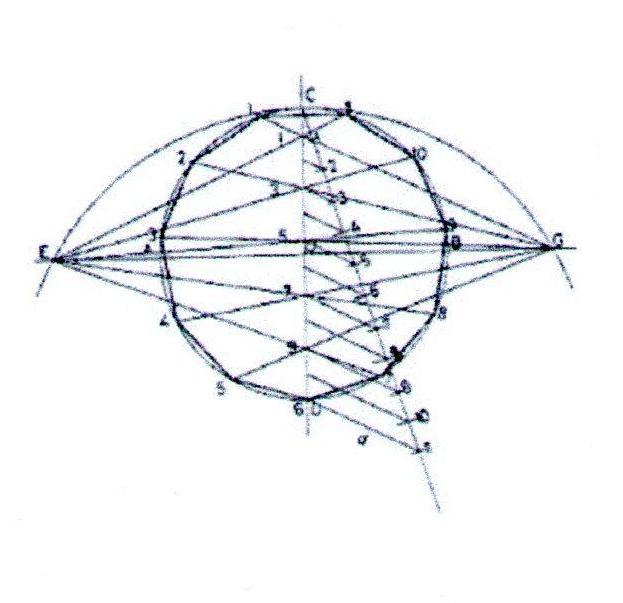
Деление окружности на пять и десять равных частей и построе­ние правильного вписанного пяти­угольника и десятиугольника пока­зано на рис. 122.

Половину любого диаметра (радиус) делят пополам (рис. 122, а), получают точку А. Из точки А, как из центра, проводят дугу радиу­сом, равным расстоянию от точки А до точки 1, до пересечения со второй половиной этого диаметра, в точке В (рис. 122, б). Отрезок 1В равен хорде, стягивающей дугу, длина которой равна 1 /₅ длины окружности. Делая засечки на окружности (рис. 122, в) радиусом R, равным отрезку 1В, делят окруж­ность на пять равных частей. Начальную точку 1 выбирают в зависимости от расположения пятиугольника. Из точки / строят точки 2 и 5 (рис. 122, в), затем из точки 2 строят точку 3, а из точки 5 строят точку 4. Расстояние от точки 3 до точки 4 проверяют циркулем; если расстояние между точками 3 и 4 равно отрезку 1В, то построения были выполнены точно. Нельзя выполнять засечки последовательно, в одну сторону, так как происходит набегание ошибок и последняя сторона пятиугольника получается перекошенной. Последовательно соединив найденные точки, получают пяти­угольник (рис. 122, г).

Деление окружности на десять равных час­тей выполняют аналогично делению окруж­ности на пять равных частей (рис. 122), но сначала делят окружность на пять частей, на­чиная построение из точки /, а затем из точ­ки 6, находящейся на противоположном конце диаметра (рис. 123, а). Соединив последова­тельно все точки, получают правильный впи­санный десятиугольник (рис. 123, б).

Деление окружности на семь и четырнадцать равных частей и по­строение правильного вписанного семиугольника и четырнадцатиугольника показано на рис. 124 и 125.

Из любой точки окружности, например точ­ки Л, радиусом заданной окружности проводят дугу (рис. 124, а) до пересечения с окруж­ностью в точках В и D. Соединим точки В и D прямой. Половина полученного отрезка (в данном случае отрезок ВС) будет равна хорде, которая стягивает дугу, составляющую 1 /₇ дли­ны окружности. Радиусом, равным отрезку ВС, делают засечки на окружности в последова­тельности, показанной на рис. 124, б. Соединив последовательно все точки, получают правиль­ный вписанный семиугольник (рис. 124, в).

Деление окружности на четырнадцать рав­ных частей выполняется делением окружности на семь равных частей два раза от двух точек (рис. 125, а).

Сначала окружность делится на семь рав­ных частей от точки /, затем то же построение выполняется от точки 8. Построенные точки соединяют последовательно прямыми линиями и получают правильный вписанный четырна-дцатиугольник (рис. 125, б).

СОПРЯЖЕНИЯ

Рассматривая детали, видим, что в их конст­рукции часто одна поверхность переходит в другую. Обычно эти переходы делают плав­ными, что повышает прочность деталей и де­лает их более удобными в работе. На чертеже поверхности изображаются линиями, которые также плавно переходят одна в другую.

На рис. 126, а изображена деталь, в которой плавные переходы одних плоскостей в другие представляют собой цилиндрические поверхнос­ти. На чертеже (рис. 126, б) эти плоскости изо­бражены прямыми линиями, а цилиндрические поверхности — дугами окружностей. Плавные переходы от одной прямой к другой в этих случаях выполняются дугой заданного радиуса.

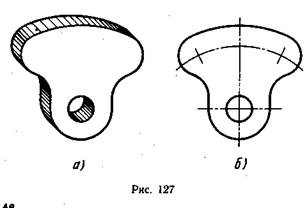
Плавный переход одной цилиндрической поверхности в другую может являться цилинд­рической поверхностью (рис. 127, а). На черте­же эти цилиндрические поверхности изобра­жены дугами окружностей, (рис. 127, б). В этом случае плавный переход одной дуги окруж­ности в другую осуществляется дугой окруж­ности заданного радиуса.

На рис. 126, а и 127, а рассмотрены простей­шие примеры плавных переходов поверхностей. В чертежах более сложных деталей плавные переходы между поверхностями изображают­ся различными сочетаниями прямых, окруж­ностей и их дуг. Вариантов таких сочетаний может быть много, но их объединяет од­но — плавность перехода. Такой плавный пе­реход одной линии (поверхности) в другую ли­нию (поверхность) называют сопряжени­ем. При построении сопряжения необходимо определить границу, где кончается одна линия и начинается другая, т. е. найти на чертеже точку перехода, которая называется точкой сопряжения или точкой касания.

Задачи на сопряжения условно можно раз­делить на три группы.

Первая группа задачвключает в себя зада­чи на построение сопряжений, где участвуют прямые линии. Это может быть непосредствен­ное касание прямой и окружности, сопряжение двух прямых дугой заданного радиуса, а также проведение касательной прямой к двум окружностям.

Построение окружности, каса­тельной к прямой, связано с нахождени­ем точки касания и центра окружности.

Задана горизонтальная прямая АВ, требует­ся построить окружность радиусом R, касательную к данной прямой (рис. 128). Точка касания выбирается произвольно. Так как точка касания не задана, то окружность ра­диуса R может коснуться данной прямой в любой точке. Таких окружностей можно про­вести множество. Центры этих окружностей (O₁, О₂ и т. д.) будут находиться на одина­ковом расстоянии от заданной прямой, т. е. на линии, расположенной параллельно заданной прямой АВ на расстоянии, равном радиусу заданной окружности (рис. 128). Назовем эту линию линией центров. Проведем линию центров параллельно прямой АВ на расстоя­нии R. Так как центр касательной окруж­ности не задан, возьмем любую точку на линии центров, например точку О. Прежде чем про­водить касательную окружность, следует опре­делить точку касания. Точка касания будет лежать на перпендикуляре, опущенном из точ­ки О на прямую АВ. В пересечении перпендику­ляра с прямой АВ получим точку К, которая будет точкой касания. Из центра О радиусом R от точки К проведем окружность. Задача решена.

В детали, которая изображена на рис. 129, а, пластина плавно переходит в цилиндр. При выполнении чертежа этой детали необходимо построить плавный переход прямой в окруж­ность.

Задача аналогична предыдущей, но до­полнена условием, что точка касания задана, так как задан размер А (рис. 129, б), который определяет величину прямолинейного участка.

Отложив размер Л, находят точку касания (точку /С), затем из точки К восставляют пер­пендикуляр, на котором откладывают радиус R заданной окружности, и находят центр ок­ружности (точку О). При обводке сначала от точки касания проводится дуга заданного ра­диуса, а потом — прямая.

Из сказанного следует:

1) центр окружности, касательной к прямой, лежит на прямой (линия центров), проведенной параллельно заданной прямой, на расстоянии, равном радиусу данной окружности;

Не нашли то, что искали? Воспользуйтесь поиском:

Как начертить правильный всьмиугольник и пяиугольник с помощью циркуля и линейки

• Попроси больше объяснений
• Следить
• Отметить нарушение

Видео:Урок по теме ЦЕНТРАЛЬНЫЕ И ВПИСАННЫЕ УГЛЫ 8 КЛАСССкачать

Ответ

Проверено экспертом

Вспомогательная задача:
Разделить данный отрезок АВ пополам или провести серединный перпендикуляр к отрезку (рис. 1 внизу)
Из концов отрезка АВ одним и тем же радиусом, большим половины отрезка АВ провести две дуги. Через точки их пересечения проводим прямую. Это серединный перпендикуляр к отрезку АВ.

Построение правильного восьмиугольника:
Проводим диаметр АВ. Строим CD — серединный перпендикуляр к АВ.
Хорду СВ делим пополам — прямая KL.
Хорду АС делим пополам — прямая MN.
Соединяем точки A, M, C, K, B, N, D и L. Получили правильный восьмиугольник.

Построение правильного пятиугольника.
Строим два перпендикулярных диаметра АВ и CD.
Делим пополам отрезок ОА — точка Е.
Из Е радиусом ЕС проводим дугу, которая пересекает ОВ в точке F.
Из С радиусом CF проводим дугу, которая пересекает окружность в точке G. CG — сторона правильного пятиугольника.
Проводим радиусом CG из точки G как из центра дугу, которая пересекает окружность в точке K. GK — вторая сторона.
И т.д.
Получаем правильный пятиугольник CGKLM.

Есть ли поблизости от Вас карандаш? Взгляните-ка на его сечение – оно представляет собой правильный шестиугольник или, как его еще называют, гексагон. Такую форму имеет также сечение гайки, поле гексагональных шахмат, кристаллическая решетка некоторых сложных молекул углерода (к примеру, графит), снежинка, пчелиные соты и другие объекты. Гигантский правильный шестиугольник был недавно обнаружен в атмосфере Сатурна. Не кажется ли странным столь частое использование природой для своих творений конструкций именно этой формы? Давайте рассмотрим эту фигуру поподробнее.

• Длина его сторон соответствует радиусу описанной окружности. Из всех геометрических фигур это свойство имеет лишь правильный шестиугольник.
• Углы равны между собой, и величина каждого составляет 120°.
• Периметр гексагона можно найти по формуле Р=6*R, если известен радиус описанной вокруг него окружности, или Р=4*√(3)*r, если окружность в него вписана. R и r – радиусы описанной и вписанной окружности.
• Площадь, которую занимает правильный шестиугольник, определяется следующим образом: S=(3*√(3)*R 2 )/2. Если радиус неизвестен, вместо него подставляем длину одной из сторон – как известно, она соответствует длине радиуса описанной окружности.

Теперь рассмотрим построение правильного шестиугольника. Есть несколько способов, самый простой из которых предполагает использование циркуля, карандаша и линейки. Вначале рисуем циркулем произвольную окружность, затем в произвольном месте на этой окружности делаем точку. Не меняя раствора циркуля, ставим острие в эту точку, отмечаем на окружности следующую насечку, продолжаем так до тех пор, пока не получим все 6 точек. Теперь остается лишь соединить их между собой прямыми отрезками, и получится искомая фигура.

Наверняка каждому из нас приходилось сталкиваться с тем, что нужно срочно что-то начертить, точный угол или многоугольник, а транспортира как нарочно под рукой нет, или Вы вообще никогда раньше ничего не чертили. Сегодня я хочу поделиться с Вами простыми схемами построения фигур на плоскости. Думаю, этот навык пригодится всем. Продолжение статьи:
http://www.livemaster.ru/topic/383001-postroenie-na-ploskosti-chast-2?ins >

Нам понадобятся: карандаш, линейка, циркуль.

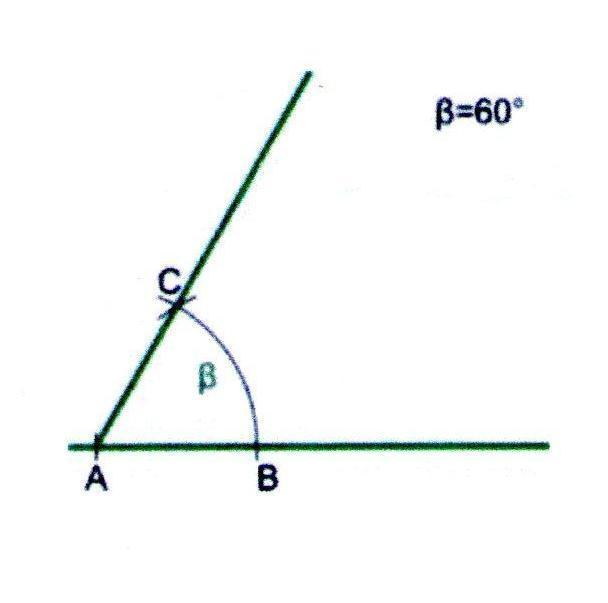
Построение угла в 60

1. Проведём прямую и отметим на ней точку А.

2. Из точки А проведём дугу произвольного радиуса и получим точку В.

3. Из точки В проведём дугу радиуса АВ, чтобы она пересекла ранее начерченную дугу.

4. Проведённая через точку пересечения (С) и точку А прямая будет второй стороной требуемого угла.

Построение угла в 45

1. Построим угол 60, кака описано выше.

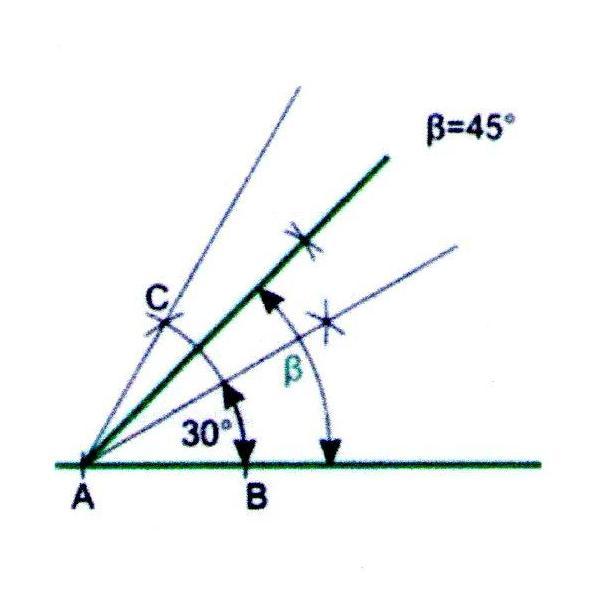
2. Разделим полученный угол пополам.

3. Угол между лучами 60 и 30 разделим пополам. В результате получим угол в 45.

Построение угла в 75

1. Построим угол в 60, как описано выше, и разделим его пополам.

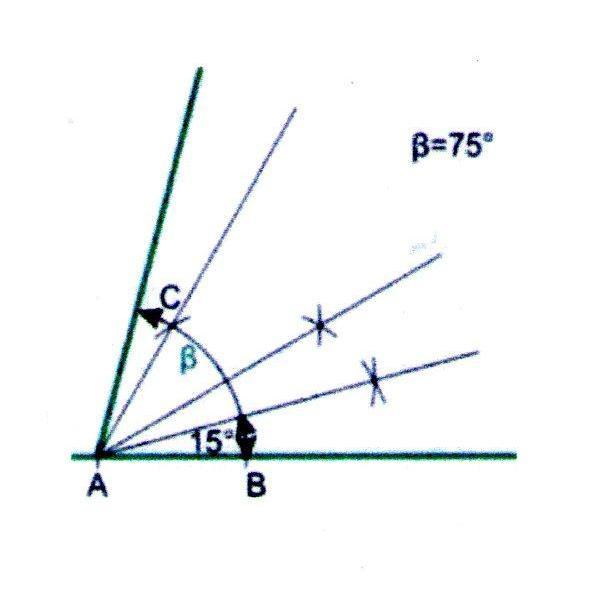
2. В ходе дальнейшего деления надвое получим угол в 15.

3. Отразим угол в 15 через луч 60 и так получим угол в 75.

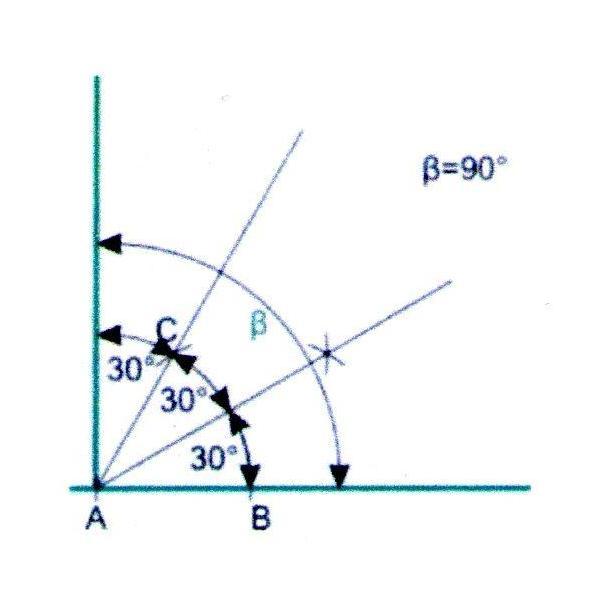
Построение угла в 90

1. Построим угол в 60, как описано выше, и разделим его пополам.

2. Получившийся угол в 30 через луч 60 и так получим угол точно в 90.

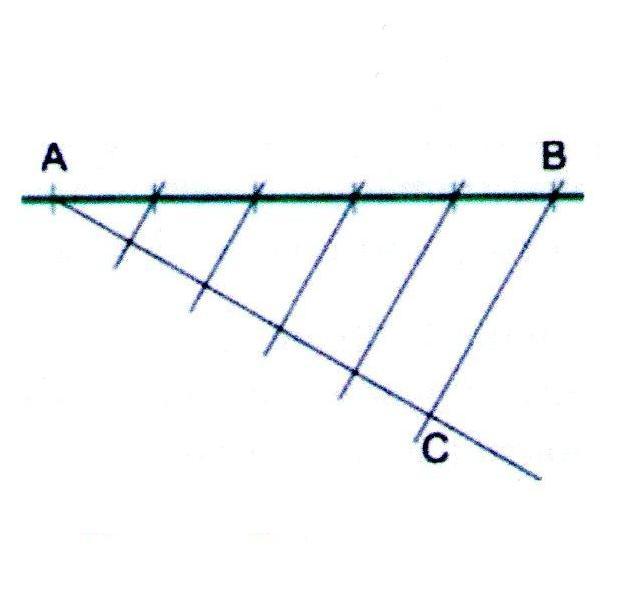
Разделение отрезка на равные части.

1. Проведём прямую и отметим на ней отрезок АВ.

2. Из точки А проведём вспомогательную прямую и разделим её на столько одинаковых частей, на сколько требуется разделить отрезок АВ. Делить будем при помощи циркуля. Последнюю точку обозначим буквой С.

3. Последнюю точка (С) соединим с концом отрезка АВ. Построим рад параллельных отрезку СВ прямых по всей длине отрезка АВ. Точки пересечения параллельных прямых с отрезком АВ и будут точками раздела отрезка на несколько равных частей.

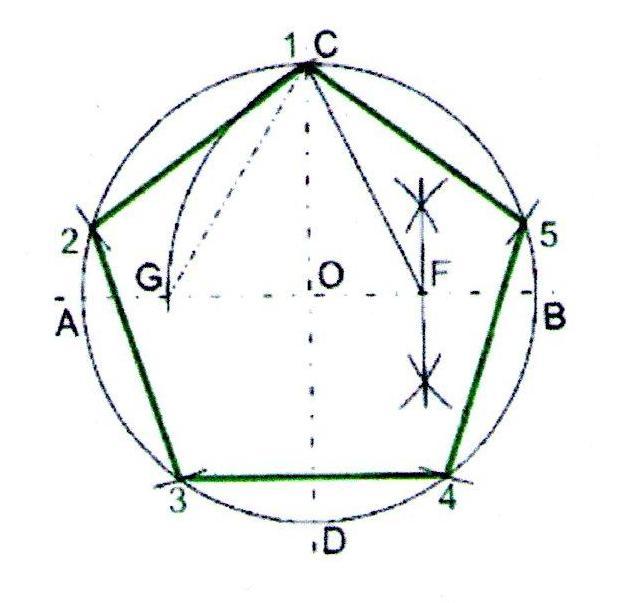
Построение правильного пятиугольника.

1. Проведём окружность радиусом 50 мм. Через центр окружности проведём взаимно перпендикулярные горизонтальную и вертикальную линии.

2. Разделим пополам расстояние ОВ. Разведём ножки циркуля на расстояние FC . Из точки F проведём дугу через С. Дуга пересечёт горизонтальную линию в точке G .

3. Расстояние CG будет длиной стороны пятиугольника. Из вершины С отложим пять раз расстояние CG .

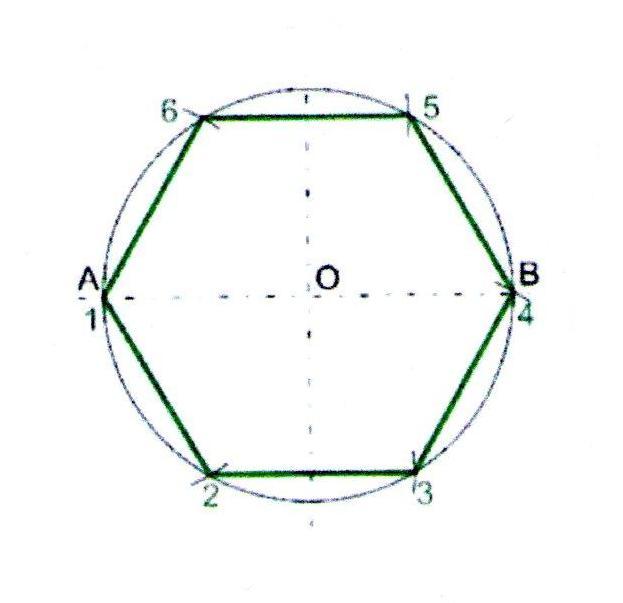
Построение правильного шестиугольника.

1. Проведём окружность радиусом 50 мм.

2. Через центр окружности проведём взаимно перпендикулярные горизонтальную и вертикальную линии.

3. Из точки А на линии окружности отложим шесть раз радиус нашей окружности. Соединив прямыми точки пересечения, получим шестиугольник.

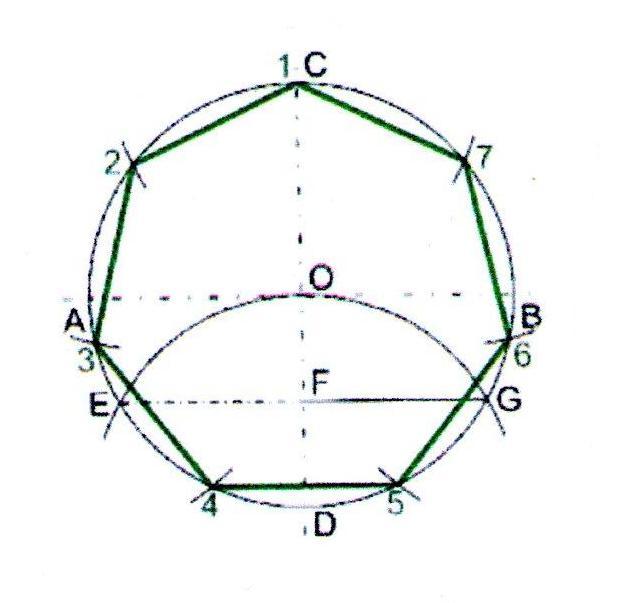
Построение правильного семиугольника.

1. Проведём окружность заданного радиуса. Через центр окружности проведём взаимно перпендикулярные горизонтальную и вертикальную линии.

2. Из точки D проведём дугу радиусом равным радиусу окружности.

3. Дуга пересечёт окружность в точках E и G .

4. Длина отрезка EF на хорде EG равна длине стороны семиугольника. Из вершины С семь раз отложим расстояние EF .

Общий метод построения многоугольников.

1. Проведём окружность радиусом 50 мм. Через центр окружности проведём взаимно перпендикулярные горизонтальную и вертикальную линии. Продолжим горизонтальную лини. За точки А и В.

2. Из точки D проведём дугу радиусом, равным радиусу окружности так, чтобы дуга пересекла горизонтальную линию.

3. При помощи вспомогательной прямой разделим вертикальную линию на столько равных частей, сколько сторон многоугольника требуется получить. Для примера показано построение одиннадцатиугольника.

4. Из точки Е проведём прямые через нечётные точки раздела вертикальной линии так, чтобы эти прямые пересекли окружность. Такую же операцию проведём из точки G . Полученные лучи пересекают окружность в точках, соединив которые прямыми получаем одиннадцатиугольник.

Первый способ — по данной стороне S с помощью транспортира.

Проводим прямую и откладываем на ней AB = S; принимаем эту линию за радиус и этим радиусом из точек A и В описываем дуги: далее с помощью транспортира строим в этих точках углы в 108°, стороны которых пересекутся с дугами в точках С и D; из этих точек радиусом АВ = 5 описываем дуги, которые пересекутся в Е, и прямыми линиями соединяем точки Л, С, Е, D, В.

Полученный пятиугольник — искомый.

Первый способ построения пятиугольника

Второй способ. Проведем окружность радиусом r. Из точки А циркулем проводим дугу радиуса AM до пересечения в точках В и С с окружностью. Соединяем В и С линией, которая пересечет горизонтальную ось в точке Е.

Затем из точки Е проводим дугу, которая пересечет горизонтальную линию в точке О. Описываем, наконец, из точки F дугу, которая пересечет окружность в точках Н и К. Отложив по окружности расстояние FO = FH = FK пять раз и соединив точки деления линиями, получим правильный пятиугольник.

Второй способ построения пятиугольника

Третий способ. В данный круг вписать правильный пятиугольник. Проводим два взаимно перпендикулярных диаметра АВ и МС. Делим радиус АО точкой Е пополам. Из точки Е, как из центра, проводим дугу окружности радиуса ЕМ и засекаем ею диаметр АВ в точке F. Отрезок MF равен стороне искомого правильного пятиугольника. Раствором циркуля, равным MF, делаем засечки N₁, Р₁, Q₁, К₁ и соединяем их прямыми.

Третий способ построения пятиугольника

На рисунке построен шестиугольник по данной стороне.

Построение шестиугольника

Прямой АВ = 5, как радиусом, из точек А и В описываем дуги, которые пересекутся в С; из этой точки тем же радиусом описываем окружность, на которой сторона А В отложится 6 раз.

Шестиугольник ADEFGB — искомый.

«Отделка комнат при ремонте»,
Н.П.Краснов

Маляру часто приходится иметь дело с правильными многоугольниками, а также треугольниками и четырехугольниками, т. е. такими фигурами, у которых все стороны и, соответственно, углы равны между собой. Может встретиться необходимость построить правильный многоугольник по данной стороне, или вписать правильный многоугольник в окружность данного радиуса, или описать его вокруг окружности. Первый вопрос сводится к нахождению внутреннего…

Построение вписанных и описанных правильных многоугольников сводится, как уже было сказано, к делению окружности на столько равных частей, сколько в многоугольнике сторон. Однако точное деление окружности путем геометрического построения возможно лишь на 3, 4, 5 и 15 равных частей, а также при делении на число частей, получаемое последовательным удвоением этих чисел. В остальных случаях приходится…

Построение овала (коробовой кривой) по данной длине АВ. Делим длину ЛВ на 3 равные части и из D и Е радиусом DF описываем дуги которые пересекутся в F и G; соединяем D и E c F и G и продолжаем эти прямые, как на фигуре; далее радиусом AD = BE из точек D и Е…

Первый способ построения. Проводим горизонтальную (АВ) и вертикальную (CD) оси и из точки их пересечения М откладываем в соответствующем масштабе полуоси. Наносим малую полуось от точки М на большой оси до точки Е. Эллипс, первый способ построения Делим BE на 2 части и одну наносим от точки М на большой оси (до F или H)…

Основанием для нанесения росписи служат полностью законченные окраской поверхности стен, потолков и других конструкций; роспись делается по высококачественным клеевым и масляным окраскам, сделанным под торцовку или флейц. Приступая к разработке эскиза отделки, мастер должен ясно представить себе всю композицию в бытовой обстановке и отчетливо осознать творческий замысел. Только при соблюдении этого основного условия можно правильно…

Видео:Как рассчитать сегменты .Скачать

Как построить правильный восьмиугольник?

Видео:Всё про углы в окружности. Геометрия | МатематикаСкачать

Как нарисовать 8 угольник без циркуля?

Нужно нарисовать квадрат, затем провести в нем диагонали. Каждую сторону следует разделить пополам. Через точку пересечения диагоналей и середину каждой стороны нужно провести отрезок, равный длине половины диагонали. Теперь осталось последовательно соединить полученные точки и вершины квадрата.

Видео:ТЕОРЕМА СИНУСОВ И ТЕОРЕМА КОСИНУСОВ. Тригонометрия | МатематикаСкачать

Как разделить окружность на 8 равных частей с помощью циркуля?

Деление окружности на восемь равных частей

Применяя известный прием деления прямого угла на две равные части при помощи циркуля или угольника строят биссектрисы прямых углов, которые пересекаясь с окружностью в точках 5, 6, 7, и 8 делят каждую четвертую часть окружности пополам.

Видео:Геометрия 9 класс (Урок№21 - Правильный многоугольник. Описанная и вписанная окружность.)Скачать

Как в окружности начертить правильный Десятиугольник?

1 способ: С помощью циркуля начертите окружность. Используя транспортир, разделите ее на 10 равных секторов по 36 градусов каждый (360:10 = 36). Затем соедините последовательно все точки, отмеченные на окружности. 2 способ: Опять же, с помощью циркуля начертите окружность.

Видео:Задача 6 №27916 ЕГЭ по математике. Урок 133Скачать

Что означает восьмиугольник?

Число восемь символизирует восстановление, обновление, возрождение, переход. Четыре стороны света плюс четыре промежуточных направления, образующие восьмиугольник, который в самых разных традициях носит название восьми ветров. .

Видео:Все об окружностях на ЕГЭ | Профильная математика 2023 | УмскулСкачать

Как построить правильный 12 угольник в окружности?

При делении окружности циркулем из четырех концов двух взаимно перпендикулярных диаметров окружности проводят радиусом, равным радиусу данной окружности, дуги до пересечения с окружностью (рис. 121). Соединив полученные точки, получают двенадцатиугольник.

Видео:8 класс, 38 урок, Вписанная окружностьСкачать

Вписанный и описанный в окружность восьмиугольник

Боковая сторона равнобедренного треугольника равна 4. Угол при вершине, противолежащий основанию, равен 120°. Найдите диаметр окружности, описанной около этого треугольника.

Воспользуемся теоремой косинусов:

(здесь a и b — боковые стороны равнобедренного треугольника, c — основание.

Диаметр описанной окружности найдем по обобщенной теореме синусов:

Вместо того, чтобы искать основание треугольника, можно было найти угол при основании. Действительно, сумма углов при основании данного равнобедренного треугольника равна 60°. Эти углы равны, поэтому каждый из них равен 30°. Применяя обобщенную теорему синусов для боковой стороны и противолежащего ей угла, получаем:

Приведем решение Андрея Ларионова.

Угол при основании равен

Следовательно, дуга описанной окружности, на которую он опирается, равна 2 · 30° = 60°. Эту дугу стягивает боковая сторона треугольника.

Хорда, стягивающая дугу в 60°, равна радиусу окружности, поэтому радиус описанной окружности равен боковой стороне треугольника, тогда D = 2 · 4 = 8.

Видео:ВПИСАННАЯ И ОПИСАННАЯ ОКРУЖНОСТЬ 😉 #егэ #математика #профильныйегэ #shorts #огэСкачать

Правильный многоугольник

Видео:9 класс, 23 урок, Окружность, вписанная в правильный многоугольникСкачать

Формулы, признаки и свойства правильного многоугольника

Многоугольником называется часть площади, которая ограничена замкнутой ломаной линией, не пересекающей сама себя.

Многоугольники отличаются между собой количеством сторон и углов.

Правильный многоугольник — это многоугольник, у которого все стороны и углы одинаковые.

Признаки правильного многоугольника

Многоугольник будет правильным, если выполняется следующее условие: все стороны и углы одинаковы.

a 1 = a 2 = a 3 = … = a n-1 = a n ,

α 1 = α 2 = α 3 = … = α n-1 = α n

где a₁ … a_n — длины сторон правильного многоугольника,
α ₁ … α _n — внутренние углы между стронами правильного многоугольника.

Основные свойства правильного многоугольника

1. Все стороны равны: a 1 = a 2 = a 3 = … = a n-1 = a n
2. Все углы равны: α 1 = α 2 = α 3 = … = α n-1 = α n
3. Центр вписанной окружности O_в совпадает с центром описанной окружности O_о, что и образуют центр многоугольникаO.
4. Сумма всех углов n-угольника равна: 180° · n — 2
5. Сумма всех внешних углов n-угольника равна 360°: β 1 + β 2 + β 3 + … + β n-1 + β n = 360°
6. Количество диагоналей (D_n) n-угольника равна половине произведения количества вершин на количество диагоналей, выходящих из каждой вершины: D n = n · n — 3 2
7. В любой многоугольник можно вписать окружность и описать круг; при этом площадь кольца, образованная этими окружностями, зависит только от длины стороны многоугольника: S = π 4 · a 2
8. Все биссектрисы углов между сторонами равны и проходят через центр правильного многоугольника O .

Видео:ПОСТРОИТЬ ПРАВИЛЬНЫЙ ПЯТИУГОЛЬНИК [construction a regular pentagon]Скачать

Формулы правильного n-угольника

Формулы длины стороны правильного n-угольника

Формула стороны правильного n-угольника через радиус вписанной окружности

a = 2 · r · tg 180° n (через градусы),

a = 2 · r · tg π n (через радианы)

Формула стороны правильного n-угольника через радиус описанной окружности

a = 2 · R · sin 180° n (через градусы),

a = 2 · R · sin π n (через радианы)

Формулы радиуса вписанной окружности правильного n-угольника

Формула радиуса вписанной окружности n-угольника через длину стороны

r = a : 2 · tg 180° n (через градусы),

r = a : 2 · tg π n (через радианы)

Формула радиуса описанной окружности правильного n-угольника

Формула радиуса описанной окружности n-угольника через длину стороны

R = a : 2 · sin 180° n (через градусы),

R = a : 2 · sin π n (через радианы)

Формулы площади правильного n-угольника

Формула площади n-угольника через длину стороны

Формула площади n-угольника через радиус вписанной окружности

Формула площади n-угольника через радиус описанной окружности

Формула периметра правильного многоугольника

Формула периметра правильного n-угольника

Периметр правильного n-угольника равен произведению длины одной стороны правильного n-угольника на количество его сторон.

Формула определения угла между сторонами правильного многоугольника

Формула угла между сторонами правильного n-угольника

Правильный треугольник

Правильный треугольник — это правильный многоугольник с тремя сторонами. Все стороны правильного треугольника равны между собой, все углы также равны и составляют 60°.

Формулы правильного треугольника

Формула стороны правильного треугольника через радиус вписанной окружности

Сторона правильного треугольника равна удвоенному произведению радиуса вписанной окружности на корень из трёх.

Формула стороны правильного треугольника через радиус описанной окружности

Сторона правильного треугольника равна произведению радиуса описанной окружности на корень из трёх.

Формула площади правильного треугольника через длину стороны

Формула площади правильного треугольника через радиус вписанной окружности

Формула площади правильного треугольника через радиус описанной окружности

Углы между сторонами правильного треугольника

Правильный четырехугольник

Правильный четырехугольник — это квадрат.

Формулы правильного четырехугольника

Формула стороны правильного четырехугольника через радиус вписанной окружности

Сторона правильного четырехугольника равна двум радиусам вписанной окружности.

Формула стороны правильного четырехугольника через радиус описанной окружности

Сторона правильного четырехугольника равна произведению радиуса описанной окружности на корень из двух.

Формула радиуса вписанной окружности правильного четырехугольника через длину стороны

Радиус вписанной окружности правильного четырехугольника равен половине стороны четырехугольника.

Формула радиуса описанной окружности правильного четырехугольника через длину стороны

Радиус описанной окружности правильного четырехугольника равен половине произведения стороны четырехугольника на корень из двух.

Формула площади правильного четырехугольника через длину стороны

Площадь правильного четырехугольника равна квадрату стороны четырехугольника.

Формула площади правильного четырехугольника через радиус вписанной окружности

Площадь правильного четырехугольника равна четырем радиусам вписанной окружности четырехугольника.

Формула площади правильного четырехугольника через радиус описанной окружности

Площадь правильного четырехугольника равна двум квадратам радиуса описанной окружности.

Углы между сторонами правильного четырехугольника

Правильный шестиугольник

Правильный шестиугольник — это правильный многоугольник с тремя сторонами. Все стороны правильного шестиугольника равны между собой, все углы также равны и составляют 120°.

Формулы правильного шестиугольник

Формула стороны правильного шестиугольника через радиус вписанной окружности

Формула стороны правильного шестиугольника через радиус описанной окружности

Длина стороны правильного шестиугольника равна радиусу описанной окружности.

Формула радиуса вписанной окружности правильного шестиугольника через длину стороны

Формула радиуса описанной окружности правильного шестиугольника через длину стороны

Формула площади правильного шестиугольника через длину стороны

Формула площади правильного шестиугольника через радиус вписанной окружности

Формула площади правильного шестиугольника через радиус описанной окружности

Углы между сторонами правильного шестиугольника

Правильный восьмиугольник

Правильный восьмиугольник — это правильный многоугольник с тремя сторонами. Все стороны правильного восьмиугольник равны между собой, все углы также равны и составляют 135°.