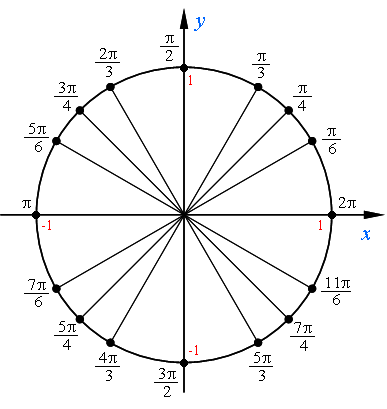
- Как обозначать числа с пи на числовой окружности?
- Обозначаем числа (2π), (π), (frac ), (-frac ), (frac )
- Обозначаем числа (frac ), (frac ), (frac )
- Обозначаем числа (frac ), (-frac ), (frac )
- Обозначаем числа (10π), (-3π), (frac ) ,(frac ), (-frac ), (-frac )
- Числам с разницей в (2πn), где (n∈Z) (то есть (n) — любое целое число) соответствует одна и та же точка.
- Точке, которой соответствует (0), также соответствуют все четные количества (π) ((±2π),(±4π),(±6π)…).
- Точке, которой соответствует (π), также соответствуют все нечетные количества (π) ((±π),(±3π),(±5π)…).
- Единичная числовая окружность на координатной плоскости
- п.1. Понятие тригонометрии
- п.2. Числовая окружность
- п.3. Градусная и радианная мера угла
- п.4. Свойства точки на числовой окружности
- п.5. Интервалы и отрезки на числовой окружности
- п.6. Примеры
- Тригонометрический круг: вся тригонометрия на одном рисунке
- А теперь подробно о тригонометрическом круге:
- 5п на 12 на числовой окружности
- расположение чисел на числовой окружности
- Числовая окружность
- Длина числовой окружности равна (2π) или примерно (6,28).
- Какие точки соответствуют числам (1), (2) и т.д?
- Чтобы отметить на числовой окружности точку соответствующую числу 1, нужно от 0 пройти расстояние равное радиусу в положительном направлении.
- Главное свойство числовой окружности
- Одному числу на числовой окружности соответствует одна точка, но одной точке соответствует множество чисел.
- Все значения одной точки на числовой окружности можно записать с помощью формулы:
- Расположение чисел на числовой окружности
- Единичная числовая окружность на координатной плоскости
- п.1. Понятие тригонометрии
- п.2. Числовая окружность
- п.3. Градусная и радианная мера угла
- п.4. Свойства точки на числовой окружности
- п.5. Интервалы и отрезки на числовой окружности
- п.6. Примеры
- Урок «Числовая окружность»
- Алгебра
- Числовая и единичная окружность
- Откладывание углов на единичной окружности
- 🔥 Видео
Видео:Как искать точки на тригонометрической окружности.Скачать

Как обозначать числа с пи на числовой окружности?
Надеюсь, вы уже прочитали про числовую окружность и знаете, почему она называется числовой, где на ней начало координат и в какой стороне положительное направление. Если нет, то бегом читать ! Если вы, конечно, собираетесь находить точки на числовой окружности.
Видео:10 класс, 11 урок, Числовая окружностьСкачать

Обозначаем числа (2π), (π), (frac ), (-frac ), (frac )
Как вы знаете из прошлой статьи, радиус числовой окружности равен (1). Значит, длина окружности равняется (2π) (вычислили по формуле (l=2πR)). С учетом этого отметим (2π) на числовой окружности. Чтобы отметить это число нужно пройти от (0) по числовой окружности расстояние равно (2π) в положительном направлении, а так как длина окружности (2π), то получается, что мы сделаем полный оборот. То есть, числу (2π) и (0) соответствует одна и та же точка. Не переживайте, несколько значений для одной точки — это нормально для числовой окружности.
Теперь обозначим на числовой окружности число (π). (π) – это половина от (2π). Таким образом, чтобы отметить это число и соответствующую ему точку, нужно пройти от (0) в положительном направлении половину окружности.
Отметим точку (frac ) . (frac ) – это половина от (π), следовательно чтобы отметить это число, нужно от (0) пройти в положительном направлении расстояние равное половине (π), то есть четверть окружности.
Обозначим на окружности точки (-) (frac ) . Двигаемся на такое же расстояние, как в прошлый раз, но в отрицательном направлении.
Нанесем (-π). Для этого пройдем расстояние равное половине окружности в отрицательном направлении.
Теперь рассмотрим пример посложнее. Отметим на окружности число (frac ) . Для этого дробь (frac ) переведем в смешанный вид (frac ) (=1) (frac ) , т.е. (frac ) (=π+) (frac ) . Значит, нужно от (0) в положительную сторону пройти расстояние в пол окружности и еще в четверть.
Задание 1. Отметьте на числовой окружности точки (-2π),(-) (frac ) .
Видео:10 класс, 12 урок, Числовая окружность на координатной плоскостиСкачать

Обозначаем числа (frac ), (frac ), (frac )
Выше мы нашли значения в точках пересечения числовой окружности с осями (x) и (y). Теперь определим положение промежуточных точек. Для начала нанесем точки (frac ) , (frac ) и (frac ) .
(frac ) – это половина от (frac ) (то есть, (frac ) (=) (frac ) (:2)) , поэтому расстояние (frac ) – это половина четверти окружности.
(frac ) – это треть от (π) (иначе говоря, (frac ) (=π:3)), поэтому расстояние (frac ) – это треть от полукруга.
(frac ) – это половина (frac ) (ведь (frac ) (=) (frac ) (:2)) поэтому расстояние (frac ) – это половина от расстояния (frac ) .
Вот так они расположены друг относительно друга:
Замечание: Расположение точек со значением (0), (frac ) ,(π), (frac ) , (frac ) , (frac ) , (frac ) лучше просто запомнить. Без них числовая окружность, как компьютер без монитора, вроде бы и полезная штука, а использовать крайне неудобно.
Разные расстояние на окружности наглядно:
Видео:3,5 способа отбора корней в тригонометрии | ЕГЭ по математике | Эйджей из ВебиумаСкачать

Обозначаем числа (frac ), (-frac ), (frac )
Обозначим на окружности точку (frac ) , для этого выполним следующие преобразования: (frac ) (=) (frac ) (=) (frac ) (+) (frac ) (=π+) (frac ) . Отсюда видно, что от нуля в положительную сторону надо пройти расстояние (π), а потом еще (frac ) .
Отметим на окружности точку (-) (frac ) . Преобразовываем: (-) (frac ) (=-) (frac ) (-) (frac ) (=-π-) (frac ) . Значит надо от (0) пройти в отрицательную сторону расстояние (π) и еще (frac ) .
Нанесем точку (frac ) , для этого преобразуем (frac ) (=) (frac ) (=) (frac ) (-) (frac ) (=2π-) (frac ) . Значит, чтобы поставить точку со значением (frac ) , надо от точки со значением (2π) пройти в отрицательную сторону расстояние (frac ) .
Видео:Отбор корней по окружностиСкачать

Обозначаем числа (10π), (-3π), (frac ) ,(frac ), (-frac ), (-frac )
Запишем (10π) в виде (5 cdot 2π). Вспоминаем, что (2π) – это расстояние равное длине окружности, поэтому чтобы отметить точку (10π), нужно от нуля пройти расстояние равное (5) окружностям. Нетрудно догадаться, что мы окажемся снова в точке (0), просто сделаем пять оборотов.
Из этого примера можно сделать вывод:
Числам с разницей в (2πn), где (n∈Z) (то есть (n) — любое целое число) соответствует одна и та же точка.
То есть, чтобы поставить число со значением больше (2π) (или меньше (-2π)), надо выделить из него целое четное количество (π) ((2π), (8π), (-10π)…) и отбросить. Тем самым мы уберем из числа, не влияющие на положение точки «пустые обороты».
Точке, которой соответствует (0), также соответствуют все четные количества (π) ((±2π),(±4π),(±6π)…).
Теперь нанесем на окружность (-3π). (-3π=-π-2π), значит (-3π) и (–π) находятся в одном месте на окружности (так как отличаются на «пустой оборот» в (-2π)).
Кстати, там же будут находиться все нечетные (π).
Точке, которой соответствует (π), также соответствуют все нечетные количества (π) ((±π),(±3π),(±5π)…).
Сейчас обозначим число (frac ) . Как обычно, преобразовываем: (frac ) (=) (frac ) (+) (frac ) (=3π+) (frac ) (=2π+π+) (frac ) . Два пи – отбрасываем, и получается что, для обозначения числа (frac ) нужно от нуля в положительную сторону пройти расстояние равное (π+) (frac ) (т.е. половину окружности и еще четверть).
Отметим (frac ) . Вновь преобразования: (frac ) (=) (frac ) (=) (frac ) (+) (frac ) (=5π+) (frac ) (=4π+π+) (frac ) . Ясно, что от нуля надо пройти расстояние равное (π+) (frac ) – и мы найдем место точки (frac ) .
Нанесем на окружность число (-) (frac ) .
(-) (frac ) (= -) (frac ) (-) (frac ) (=-10π-) (frac ) . Значит, место (-) (frac ) совпадает с местом числа (-) (frac ) .
Обозначим (-) (frac ) .
(-) (frac ) (=-) (frac ) (+) (frac ) (=-5π+) (frac ) (=-4π-π+) (frac ) . Для обозначение (-) (frac ) , на числовой окружности надо от точки со значением (–π) пройти в положительную сторону (frac ) .
Видео:Щелчок по математике I №5,6,12 Тригонометрия с нуля и до ЕГЭ за 4 часаСкачать

Единичная числовая окружность на координатной плоскости
п.1. Понятие тригонометрии
Тригонометрия берёт своё начало в Древней Греции. Само слово «тригонометрия» по-гречески означает «измерение треугольников». Эта наука в течение тысячелетий используется землемерами, архитекторами и астрономами.
Начиная с Нового времени, тригонометрия заняла прочное место в физике, в частности, при описании периодических процессов. Например, переменный ток в розетке генерируется в периодическом процессе. Поэтому любой электрический или электронный прибор у вас в доме: компьютер, смартфон, микроволновка и т.п., — спроектирован с использованием тригонометрии.
Базовым объектом изучения в тригонометрии является угол.
Предметом изучения тригонометрии как раздела математики выступают:
1) взаимосвязи между углами и сторонами треугольника, которые называют тригонометрическими функциями;
2) использование тригонометрических функций в геометрии.
п.2. Числовая окружность
Мы уже знакомы с числовой прямой (см. §16 справочника для 8 класса) и координатной плоскостью (см. §35 справочника для 7 класса), с помощью которых создаются графические представления числовых промежутков и функций. Это удобный инструмент моделирования, с помощью которого можно провести анализ, начертить график, найти область допустимых значений и решить задачу.
Для работы с углами и их функциями существует аналогичный инструмент – числовая окружность.
 | Числовая окружность (тригонометрический круг) – это окружность единичного радиуса R=1 с центром в начале координат (0;0). Точка с координатами (1;0) является началом отсчета , ей соответствует угол, равный 0. Углы на числовой окружности отсчитываются против часовой стрелки. Направление движения против часовой стрелки является положительным ; по часовой стрелке – отрицательным . |
| Отметим на числовой окружности углы 30°, 45°, 90°, 120°, 180°, а также –30°, –45°, –90°, –120°, –180°. |  |
п.3. Градусная и радианная мера угла
Углы можно измерять в градусах или в радианах.
Известно, что развернутый угол, дуга которого равна половине окружности, равен 180°. Прямой угол, дуга которого равна четверти окружности, равен 90°. Тогда полная, замкнутая дуга окружности составляет 360°.
Приписывание развернутому углу меры в 180°, а прямому 90°, достаточно произвольно и уходит корнями в далёкое прошлое. С таким же успехом это могло быть 100° и 50°, или 200° и 100° (что, кстати, предлагалось одним из декретов во времена французской революции 1789 г.).
В целом, более обоснованной и естественной для измерения углов является радианная мера.
 | Найдем радианную меру прямого угла ∠AOB=90°. Построим окружность произвольного радиуса r с центром в вершине угла – точке O. Длина этой окружности: L=2πr. Длина дуги AB: (l_=frac =frac =frac .) Тогда радианная мера угла: $$ angle AOB=frac =frac =frac $$ |
| 30° | 45° | 60° | 90° | 120° | 135° | 150° | 180° | 270° | 360° |
| (frac ) | (frac ) | (frac ) | (frac ) | (frac ) | (frac ) | (frac ) | (pi) | (frac ) | (2pi) |
п.4. Свойства точки на числовой окружности
Построим числовую окружность. Обозначим O(0;0), A(1;0)
 | Каждому действительному числу t на числовой окружности соответствует точка Μ(t). При t=0, M(0)=A. При t>0 двигаемся по окружности против часовой стрелки, описывая дугу ⌒ AM=t. Точка M — искомая. При t Например: |
| Отметим на числовой окружности точки, соответствующие (frac , frac , frac , frac , pi), а также (-frac , -frac , -frac , -frac , -pi) Для этого нужно отложить углы 30°, 45°, 90°, 120°, 180° и –30°, –45°, –90°, –120°, –180° с вершиной в начале координат и отметить соответствующие дуги на числовой окружности. |  |
| Отметим на числовой окружности точки, соответствующие (frac , frac , frac ), и (-frac ). Все четыре точки совпадают, т.к. begin Mleft(frac right)=Mleft(frac +2pi kright)\ frac -2pi=-frac \ frac +2pi=frac \ frac +4pi=frac end |  |
п.5. Интервалы и отрезки на числовой окружности
Каждому действительному числу соответствует точка на числовой окружности. Соответственно, числовые промежутки (см. §16 справочника для 8 класса) получают свои отображения в виде дуг.
| Числовой промежуток | Соответствующая дуга числовой окружности |
| Отрезок | |
$$ -frac lt t lt frac $$  а также, с учетом периода $$ -frac +2pi klt tltfrac +2pi k $$ |  |
| Интервал | |
$$ -frac leq t leq frac $$  а также, с учетом периода $$ -frac +2pi kleq tleqfrac +2pi k $$ |  |
| Полуинтервал | |
$$ -frac leq t ltfrac $$  а также, с учетом периода $$ -frac +2pi kleq tltfrac +2pi k $$ |  |
п.6. Примеры
Пример 1. Точка E делит числовую окружность во второй четверти в отношении 1:2.
Чему равны дуги AE, BE, EC, ED в градусах и радианах?
Угловая мера четверти 90°. При делении в отношении 1:2 получаем дуги 30° и 60° соответственно: begin BE=30^ =frac .\ EC=60^ =frac .\ AE=EC+CD=90^ +30^ =120^ =frac .\ ED=EC+CD=60^ +90^ =150^ =frac . end
Пример 2. Найдите на числовой окружности точку, соответствующую данному числу: (-frac ; frac ; frac ; frac ).
| Находим соответствующие углы в градусах и откладываем с помощью транспортира (положительные – против часовой стрелки, отрицательные – по часовой стрелке), отмечаем соответствующие точки на числовой окружности. begin -frac =-90^ , frac =135^ \ frac =210^ , frac =315^ end |  |
Пример 3. Найдите на числовой окружности точку, соответствующую данному числу: (-frac ; 5pi; frac ; frac ).
| Выделяем из дроби целую часть, отнимаем/прибавляем один или больше полных оборотов (2πk — четное количество π), чтобы попасть в промежуток от 0 до 2π. Далее – действуем, как в примере 2. begin -frac =frac cdotpi=-6pi+frac rightarrow frac =90^ \ 5pi=4pi+pirightarrow pi=180^ \ frac =frac pi=3pi-frac rightarrow pi-frac =frac \ frac =frac pi=7pi-frac rightarrow pi-frac =frac end |  |
Пример 4. В какой четверти числовой окружности находится точка, соответствующая числу: 2; 4; 5; 7.
 | Сравниваем каждое число с границами четвертей: begin 0, fracpi2approxfrac =1,57, piapprox 3,14\ 3pi 3cdot 3,14\ frac approx frac =4,71, 2piapprox 6,28 end |
(fracpi2lt 2lt pi Rightarrow ) угол 2 радиана находится во 2-й четверти
(pilt 4lt frac Rightarrow ) угол 4 радиана находится в 3-й четверти
(frac lt 5lt 2pi Rightarrow ) угол 5 радиана находится в 4-й четверти
(7gt 2pi), отнимаем полный оборот: (0lt 7-2pilt fracpi2Rightarrow) угол 7 радиан находится в 1-й четверти.
Пример 5. Изобразите на числовой окружности множество точек ((kinmathbb )), запишите количество полученных базовых точек.
| $$ frac $$ | $$ -frac +2pi k $$ |
 Четыре базовых точки, через каждые 90° |  Две базовых точки, через каждые 180° |
| $$ frac +frac $$ | $$ -frac $$ |
 Три базовых точки, через каждые 120° |  Пять базовых точек, через каждые 72° |
Пример 6. Изобразите на числовой окружности дуги, соответствующие числовым промежуткам.
Видео:18+ Математика без Ху!ни. Формулы ПриведенияСкачать

Тригонометрический круг: вся тригонометрия на одном рисунке
Тригонометрический круг — это самый простой способ начать осваивать тригонометрию. Он легко запоминается, и на нём есть всё необходимое.
Тригонометрический круг заменяет десяток таблиц.
Вот что мы видим на этом рисунке:
Видео:Задание №13. Как отбирать корни в тригонометрической окружности? 🤔Скачать

А теперь подробно о тригонометрическом круге:
Нарисована единичная окружность — то есть окружность с радиусом, равным единице, и с центром в начале системы координат. Той самой системы координат с осями и , в которой мы привыкли рисовать графики функций.
Мы отсчитываем углы от положительного направления оси против часовой стрелки.
Полный круг — градусов.
Точка с координатами соответствует углу ноль градусов. Точка с координатами отвечает углу в , точка с координатами — углу в . Каждому углу от нуля до градусов соответствует точка на единичной окружности.
Косинусом угла называется абсцисса (то есть координата по оси ) точки на единичной окружности, соответствущей данному углу .
Синусом угла называется ордината (то есть координата по оси ) точки на единичной окружности, соответствущей данному углу .
Всё это легко увидеть на нашем рисунке.
Итак, косинус и синус — координаты точки на единичной окружности, соответствующей данному углу. Косинус — абсцисса , синус — ордината . Поскольку окружность единичная, для любого угла и синус, и косинус находятся в пределах от до :
Простым следствием теоремы Пифагора является основное тригонометрическое тождество:
Для того, чтобы узнать знаки синуса и косинуса какого-либо угла, не нужно рисовать отдельных таблиц. Всё уже нарисовано! Находим на нашей окружности точку, соответствующую данному углу , смотрим, положительны или отрицательны ее координаты по (это косинус угла ) и по (это синус угла ).
Принято использовать две единицы измерения углов: градусы и радианы. Перевести градусы в радианы просто: градусов, то есть полный круг, соответствует радиан. На нашем рисунке подписаны и градусы, и радианы.
Если отсчитывать угол от нуля против часовой стрелки — он положительный. Если отсчитывать по часовой стрелке — угол будет отрицательным. Например, угол — это угол величиной в , который отложили от положительного направления оси по часовой стрелке.
Легко заметить, что
Углы могут быть и больше градусов. Например, угол — это два полных оборота по часовой стрелке и еще . Поскольку, сделав несколько полных оборотов по окружности, мы возвращаемся в ту же точку с теми же координатами по и по , значения синуса и косинуса повторяются через . То есть:
где — целое число. То же самое можно записать в радианах:
Можно на том же рисунке изобразить ещё и оси тангенсов и котангенсов, но проще посчитать их значения. По определению,
Видео:Реакция на результаты ЕГЭ 2022 по русскому языкуСкачать

5п на 12 на числовой окружности
Числовая окружность – это единичная окружность, точки которой соответствуют определенным действительным числам.
Единичной окружностью называют окружность радиуса 1.
Общий вид числовой окружности.
1) Ее радиус принимается за единицу измерения.
2) Горизонтальный и вертикальный диаметры делят числовую окружность на четыре четверти (см.рисунок). Их соответственно называют первой, второй, третьей и четвертой четвертью.
3) Горизонтальный диаметр обозначают AC, причем А – это крайняя правая точка.
Вертикальный диаметр обозначают BD, причем B – это крайняя верхняя точка.
Соответственно:
первая четверть – это дуга AB
вторая четверть – дуга BC
третья четверть – дуга CD
четвертая четверть – дуга DA
4) Начальная точка числовой окружности – точка А.
Отсчет по числовой окружности может вестись как по часовой стрелке, так и против часовой стрелки.
Отсчет от точки А против часовой стрелки называется положительным направлением.
Отсчет от точки А по часовой стрелке называется отрицательным направлением.
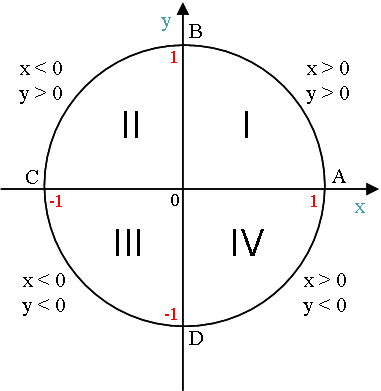
Центр радиуса числовой окружности соответствует началу координат (числу 0).
Горизонтальный диаметр соответствует оси x, вертикальный – оси y.
Начальная точка А числовой окружности находится на оси x и имеет координаты (1; 0).
Значения x и y в четвертях числовой окружности:
x 0, y Основные величины числовой окружности:
Величина
в радианах
Величина
в радиусах
Имена и местонахождение основных точек числовой окружности:
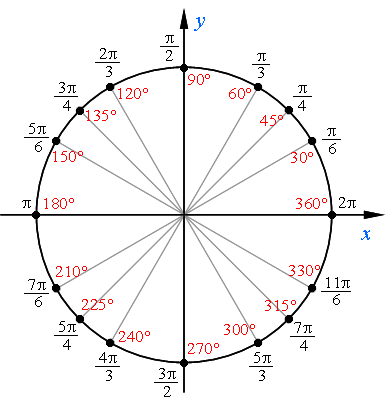
Как запомнить имена числовой окружности.
Есть несколько простых закономерностей, которые помогут вам легко запомнить основные имена числовой окружности.
Перед тем как начать, напомним: отсчет ведется в положительном направлении, то есть от точки А (2π) против часовой стрелки.
1) Начнем с крайних точек на осях координат.
Начальная точка – это 2π (крайняя правая точка на оси х, равная 1).
Как вы знаете, 2π – это длина окружности. Значит, половина окружности – это 1π или π. Ось х делит окружность как раз пополам. Соответственно, крайняя левая точка на оси х, равная -1, называется π.
Крайняя верхняя точка на оси у, равная 1, делит верхнюю полуокружность пополам. Значит, если полуокружность – это π, то половина полуокружности – это π/2.
Одновременно π/2 – это и четверть окружности. Отсчитаем три таких четверти от первой до третьей – и мы придем в крайнюю нижнюю точку на оси у, равной -1. Но если она включает три четверти – значит имя ей 3π/2.
2) Теперь перейдем к остальным точкам. Обратите внимание: все противоположные точки имеют одинаковый числитель – причем это противоположные точки и относительно оси у, и относительно центра осей, и относительно оси х. Это нам и поможет знать их значения точек без зубрежки.
Надо запомнить лишь значение точек первой четверти: π/6, π/4 и π/3. И тогда мы «увидим» некоторые закономерности:
— Относительно оси у в точках второй четверти, противоположных точкам первой четверти, числа в числителях на 1 меньше величины знаменателей. К примеру, возьмем точку π/6. Противоположная ей точка относительно оси у тоже в знаменателе имеет 6, а в числителе 5 (на 1 меньше). То есть имя этой точки: 5π/6. Точка, противоположная π/4, тоже имеет в знаменателе 4, а в числителе 3 (на 1 меньше, чем 4) – то есть это точка 3π/4.
Точка, противоположная π/3, тоже имеет в знаменателе 3, а в числителе на 1 меньше: 2π/3.
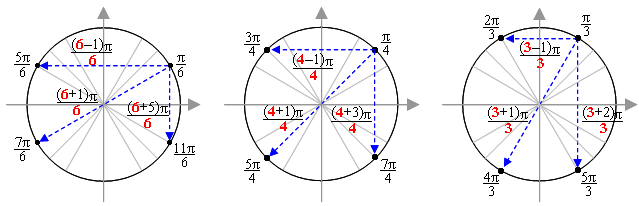
Точка, противоположная точке π/4, тоже имеет в знаменателе 4, а в числителе число на 1 больше: 5π/4.
Точка, противоположная точке π/3, тоже имеет в знаменателе 3, а в числителе число на 1 больше: 4π/3.
— Относительно оси х (четвертая четверть) дело посложнее. Здесь надо к величине знаменателя прибавить число, которое на 1 меньше – эта сумма и будет равна числовой части числителя противоположной точки. Начнем опять с π/6. Прибавим к величине знаменателя, равной 6, число, которое на 1 меньше этого числа – то есть 5. Получаем: 6 + 5 = 11. Значит, противоположная ей относительно оси х точка будет иметь в знаменателе 6, а в числителе 11 – то есть 11π/6.
Точка π/4. Прибавляем к величине знаменателя число на 1 меньше: 4 + 3 = 7. Значит, противоположная ей относительно оси х точка имеет в знаменателе 4, а в числителе 7 – то есть 7π/4.
Точка π/3. Знаменатель равен 3. Прибавляем к 3 на единицу меньшее число – то есть 2. Получаем 5. Значит, противоположная ей точка имеет в числителе 5 – и это точка 5π/3.
3) Еще одна закономерность для точек середин четвертей. Понятно, что их знаменатель равен 4. Обратим внимание на числители. Числитель середины первой четверти – это 1π (но 1 не принято писать). Числитель середины второй четверти – это 3π. Числитель середины третьей четверти – это 5π. Числитель середины четвертой четверти – это 7π. Получается, что в числителях середин четвертей – четыре первых нечетных числа в порядке их возрастания:
(1)π, 3π, 5π, 7π.
Это тоже очень просто. Поскольку середины всех четвертей имеют в знаменателе 4, то мы уже знаем их полные имена: π/4, 3π/4, 5π/4, 7π/4.
Особенности числовой окружности. Сравнение с числовой прямой.
Как вы знаете, на числовой прямой каждая точка соответствует единственному числу. К примеру, если точка А на прямой равна 3, то она уже не может равняться никакому другому числу.
На числовой окружности все иначе, поскольку это окружность. К примеру, чтобы из точки А окружности прийти к точке M, можно сделать это, как на прямой (только пройдя дугу), а можно и обогнуть целый круг, а потом уже прийти к точке M. Вывод:
Пусть точка M равна какому-то числу t. Как мы знаем, длина окружности равна 2π. Значит, точку окружности t мы можем записать двояко: t или t + 2π. Это равнозначные величины.
То есть t = t + 2π. Разница лишь в том, что в первом случае вы пришли к точке M сразу, не делая круга, а во втором случае вы совершили круг, но в итоге оказались в той же точке M. Таких кругов можно сделать и два, и три, и двести. Если обозначить количество кругов буквой k, то получим новое выражение:
t = t + 2πk.
Отсюда формула:
Если точка M числовой окружности равна числу t, то она равна и числу вида t + 2πk, где k – любое целое число:
M(t) = M(t + 2πk),
где k ∈ Z.
Число k называется параметром.
Уравнение числовой окружности
(второе уравнение – в разделе «Синус, косинус, тангенс, котангенс»):
Видео:Деление окружности на 3; 6; 12 равных частейСкачать

расположение чисел на числовой окружности
Видео:Деление окружности на пять равных частей. Урок 7. (Часть 1. ГЕОМЕТРИЧЕСКИЕ ПОСТРОЕНИЯ)Скачать

Числовая окружность
1) Начало отсчета находится в крайней правой точке окружности;
3) Если в положительном направлении отложить на окружности расстояние (t), то мы попадем в точку со значением (t);
4) Если в отрицательном направлении отложить на окружности расстояние (t), то мы попадем в точку со значением (–t).
Почему окружность называется числовой?
Потому что на ней обозначаются числа. В этом окружность похожа на числовую ось – на окружности, как и на оси, для каждого числа есть определенная точка.
Зачем знать, что такое числовая окружность?
С помощью числовой окружности определяют значение синусов, косинусов, тангенсов и котангенсов. Поэтому для знания тригонометрии и сдачи ЕГЭ на 60+ баллов, обязательно нужно понимать, что такое числовая окружность и как на ней расставить точки.
Что в определении означают слова «…единичного радиуса…»?
Это значит, что радиус этой окружности равен (1). И если мы построим такую окружность с центром в начале координат, то она будет пересекаться с осями в точках (1) и (-1).
Ее не обязательно рисовать маленькой, можно изменить «размер» делений по осям, тогда картинка будет крупнее (см. ниже).
Почему радиус именно единица? Так удобнее, ведь в этом случае при вычислении длины окружности с помощью формулы (l=2πR) мы получим:
Длина числовой окружности равна (2π) или примерно (6,28).
Тут важно не путать начало отсчета на координатной прямой и на числовой окружности – это две разные системы отсчета! А так же не путайте (1) на оси (x) и (0) на окружности – это точки на разных объектах.
Видео:Деление окружности на 5 равных частейСкачать
Какие точки соответствуют числам (1), (2) и т.д?
Помните, мы приняли, что у числовой окружности радиус равен (1)? Это и будет нашим единичным отрезком (по аналогии с числовой осью), который мы будем откладывать на окружности.
Чтобы отметить на числовой окружности точку соответствующую числу 1, нужно от 0 пройти расстояние равное радиусу в положительном направлении.
Чтобы отметить на окружности точку соответствующую числу (2), нужно пройти расстояние равное двум радиусам от начала отсчета, чтобы (3) – расстояние равное трем радиусам и т.д.
При взгляде на эту картинку у вас могут возникнуть 2 вопроса:
1. Что будет, когда окружность «закончится» (т.е. мы сделаем полный оборот)?
Ответ: пойдем на второй круг! А когда и второй закончится, пойдем на третий и так далее. Поэтому на окружность можно нанести бесконечное количество чисел.
2. Где будут отрицательные числа?
Ответ: там же! Их можно так же расставить, отсчитывая от нуля нужное количество радиусов, но теперь в отрицательном направлении.
К сожалению, обозначать на числовой окружности целые числа затруднительно. Это связано с тем, что длина числовой окружности будет равна не целому числу: (2π). И на самых удобных местах (в точках пересечения с осями) тоже будут не целые числа, а доли числа (π) : ( frac ),(-frac ),(frac ), (2π). Поэтому при работе с окружностью чаще используют числа с (π). Обозначать такие числа гораздо проще (как это делается можете прочитать в этой статье ).
Видео:Отбор корней по окружностиСкачать

Главное свойство числовой окружности
Одному числу на числовой окружности соответствует одна точка, но одной точке соответствует множество чисел.
Такая вот математическая полигамия.
И следствие из этого правила:
Все значения одной точки на числовой окружности можно записать с помощью формулы:
Что надо запомнить про числовую окружность:
Видео:Длина окружности. Площадь круга. 6 класс.Скачать

Расположение чисел на числовой окружности
Числовая окружность – это единичная окружность, точки которой соответствуют определенным действительным числам.
Единичной окружностью называют окружность радиуса 1.
Общий вид числовой окружности.
1) Ее радиус принимается за единицу измерения.
2) Горизонтальный и вертикальный диаметры делят числовую окружность на четыре четверти (см.рисунок). Их соответственно называют первой, второй, третьей и четвертой четвертью.
3) Горизонтальный диаметр обозначают AC, причем А – это крайняя правая точка.
Вертикальный диаметр обозначают BD, причем B – это крайняя верхняя точка.
Соответственно:
первая четверть – это дуга AB
вторая четверть – дуга BC
третья четверть – дуга CD
четвертая четверть – дуга DA
4) Начальная точка числовой окружности – точка А.
Отсчет по числовой окружности может вестись как по часовой стрелке, так и против часовой стрелки.
Отсчет от точки А против часовой стрелки называется положительным направлением.
Отсчет от точки А по часовой стрелке называется отрицательным направлением.

Центр радиуса числовой окружности соответствует началу координат (числу 0).
Горизонтальный диаметр соответствует оси x, вертикальный – оси y.
Начальная точка А числовой окружности находится на оси x и имеет координаты (1; 0).
Значения x и y в четвертях числовой окружности:
x 0, y Основные величины числовой окружности:
Величина
в радианах
Величина
в радиусах
Имена и местонахождение основных точек числовой окружности:
Как запомнить имена числовой окружности.
Есть несколько простых закономерностей, которые помогут вам легко запомнить основные имена числовой окружности.
Перед тем как начать, напомним: отсчет ведется в положительном направлении, то есть от точки А (2π) против часовой стрелки.
1) Начнем с крайних точек на осях координат.
Начальная точка – это 2π (крайняя правая точка на оси х, равная 1).
Крайняя верхняя точка на оси у, равная 1, делит верхнюю полуокружность пополам. Значит, если полуокружность – это π, то половина полуокружности – это π/2.
2) Теперь перейдем к остальным точкам. Обратите внимание: все противоположные точки имеют одинаковый числитель – причем это противоположные точки и относительно оси у, и относительно центра осей, и относительно оси х. Это нам и поможет знать их значения точек без зубрежки.
Надо запомнить лишь значение точек первой четверти: π/6, π/4 и π/3. И тогда мы «увидим» некоторые закономерности:
— Относительно оси у в точках второй четверти, противоположных точкам первой четверти, числа в числителях на 1 меньше величины знаменателей. К примеру, возьмем точку π/6. Противоположная ей точка относительно оси у тоже в знаменателе имеет 6, а в числителе 5 (на 1 меньше). То есть имя этой точки: 5π/6. Точка, противоположная π/4, тоже имеет в знаменателе 4, а в числителе 3 (на 1 меньше, чем 4) – то есть это точка 3π/4.
Точка, противоположная π/3, тоже имеет в знаменателе 3, а в числителе на 1 меньше: 2π/3.

Точка, противоположная точке π/4, тоже имеет в знаменателе 4, а в числителе число на 1 больше: 5π/4.
Точка, противоположная точке π/3, тоже имеет в знаменателе 3, а в числителе число на 1 больше: 4π/3.
— Относительно оси х (четвертая четверть) дело посложнее. Здесь надо к величине знаменателя прибавить число, которое на 1 меньше – эта сумма и будет равна числовой части числителя противоположной точки. Начнем опять с π/6. Прибавим к величине знаменателя, равной 6, число, которое на 1 меньше этого числа – то есть 5. Получаем: 6 + 5 = 11. Значит, противоположная ей относительно оси х точка будет иметь в знаменателе 6, а в числителе 11 – то есть 11π/6.
Точка π/4. Прибавляем к величине знаменателя число на 1 меньше: 4 + 3 = 7. Значит, противоположная ей относительно оси х точка имеет в знаменателе 4, а в числителе 7 – то есть 7π/4.
Точка π/3. Знаменатель равен 3. Прибавляем к 3 на единицу меньшее число – то есть 2. Получаем 5. Значит, противоположная ей точка имеет в числителе 5 – и это точка 5π/3.
3) Еще одна закономерность для точек середин четвертей. Понятно, что их знаменатель равен 4. Обратим внимание на числители. Числитель середины первой четверти – это 1π (но 1 не принято писать). Числитель середины второй четверти – это 3π. Числитель середины третьей четверти – это 5π. Числитель середины четвертой четверти – это 7π. Получается, что в числителях середин четвертей – четыре первых нечетных числа в порядке их возрастания:
(1)π, 3π, 5π, 7π.
Это тоже очень просто. Поскольку середины всех четвертей имеют в знаменателе 4, то мы уже знаем их полные имена: π/4, 3π/4, 5π/4, 7π/4.
Особенности числовой окружности. Сравнение с числовой прямой.
Как вы знаете, на числовой прямой каждая точка соответствует единственному числу. К примеру, если точка А на прямой равна 3, то она уже не может равняться никакому другому числу.
На числовой окружности все иначе, поскольку это окружность. К примеру, чтобы из точки А окружности прийти к точке M, можно сделать это, как на прямой (только пройдя дугу), а можно и обогнуть целый круг, а потом уже прийти к точке M. Вывод:
Пусть точка M равна какому-то числу t. Как мы знаем, длина окружности равна 2π. Значит, точку окружности t мы можем записать двояко: t или t + 2π. Это равнозначные величины.
То есть t = t + 2π. Разница лишь в том, что в первом случае вы пришли к точке M сразу, не делая круга, а во втором случае вы совершили круг, но в итоге оказались в той же точке M. Таких кругов можно сделать и два, и три, и двести. Если обозначить количество кругов буквой k, то получим новое выражение:
t = t + 2πk.
Отсюда формула:
Если точка M числовой окружности равна числу t, то она равна и числу вида t + 2πk, где k – любое целое число:
M(t) = M(t + 2πk),
где k ∈ Z.
Число k называется параметром.
Уравнение числовой окружности
(второе уравнение – в разделе «Синус, косинус, тангенс, котангенс»):
Видео:Выборка с помощью окружностиСкачать

Единичная числовая окружность на координатной плоскости
п.1. Понятие тригонометрии
Базовым объектом изучения в тригонометрии является угол.
Предметом изучения тригонометрии как раздела математики выступают:
1) взаимосвязи между углами и сторонами треугольника, которые называют тригонометрическими функциями;
2) использование тригонометрических функций в геометрии.
п.2. Числовая окружность
Мы уже знакомы с числовой прямой (см. §16 справочника для 8 класса) и координатной плоскостью (см. §35 справочника для 7 класса), с помощью которых создаются графические представления числовых промежутков и функций. Это удобный инструмент моделирования, с помощью которого можно провести анализ, начертить график, найти область допустимых значений и решить задачу.
Для работы с углами и их функциями существует аналогичный инструмент – числовая окружность.
| Отметим на числовой окружности углы 30°, 45°, 90°, 120°, 180°, а также –30°, –45°, –90°, –120°, –180°. |  |
п.3. Градусная и радианная мера угла
Углы можно измерять в градусах или в радианах.
Известно, что развернутый угол, дуга которого равна половине окружности, равен 180°. Прямой угол, дуга которого равна четверти окружности, равен 90°. Тогда полная, замкнутая дуга окружности составляет 360°.
Приписывание развернутому углу меры в 180°, а прямому 90°, достаточно произвольно и уходит корнями в далёкое прошлое. С таким же успехом это могло быть 100° и 50°, или 200° и 100° (что, кстати, предлагалось одним из декретов во времена французской революции 1789 г.).
В целом, более обоснованной и естественной для измерения углов является радианная мера.
| 30° | 45° | 60° | 90° | 120° | 135° | 150° | 180° | 270° | 360° |
| (frac ) | (frac ) | (frac ) | (frac ) | (frac ) | (frac ) | (frac ) | (pi) | (frac ) | (2pi) |
п.4. Свойства точки на числовой окружности
Построим числовую окружность. Обозначим O(0;0), A(1;0)
| Отметим на числовой окружности точки, соответствующие (frac , frac , frac ), и (-frac ). Все четыре точки совпадают, т.к. begin Mleft(frac right)=Mleft(frac +2pi kright)\ frac -2pi=-frac \ frac +2pi=frac \ frac +4pi=frac end |  |
п.5. Интервалы и отрезки на числовой окружности
Каждому действительному числу соответствует точка на числовой окружности. Соответственно, числовые промежутки (см. §16 справочника для 8 класса) получают свои отображения в виде дуг.
п.6. Примеры
Пример 1. Точка E делит числовую окружность во второй четверти в отношении 1:2.
Чему равны дуги AE, BE, EC, ED в градусах и радианах?
Угловая мера четверти 90°. При делении в отношении 1:2 получаем дуги 30° и 60° соответственно: begin BE=30^ =frac .\ EC=60^ =frac .\ AE=EC+CD=90^ +30^ =120^ =frac .\ ED=EC+CD=60^ +90^ =150^ =frac . end
Пример 2. Найдите на числовой окружности точку, соответствующую данному числу: (-frac ; frac ; frac ; frac ).
| Находим соответствующие углы в градусах и откладываем с помощью транспортира (положительные – против часовой стрелки, отрицательные – по часовой стрелке), отмечаем соответствующие точки на числовой окружности. begin -frac =-90^ , frac =135^ \ frac =210^ , frac =315^ end |  |
Пример 3. Найдите на числовой окружности точку, соответствующую данному числу: (-frac ; 5pi; frac ; frac ).
Пример 4. В какой четверти числовой окружности находится точка, соответствующая числу: 2; 4; 5; 7.
 | Сравниваем каждое число с границами четвертей: begin 0, fracpi2approxfrac =1,57, piapprox 3,14\ 3pi 3cdot 3,14\ frac approx frac =4,71, 2piapprox 6,28 end |
(fracpi2lt 2lt pi Rightarrow ) угол 2 радиана находится во 2-й четверти
(pilt 4lt frac Rightarrow ) угол 4 радиана находится в 3-й четверти
(frac lt 5lt 2pi Rightarrow ) угол 5 радиана находится в 4-й четверти
(7gt 2pi), отнимаем полный оборот: (0lt 7-2pilt fracpi2Rightarrow) угол 7 радиан находится в 1-й четверти.
Пример 5. Изобразите на числовой окружности множество точек ((kinmathbb )), запишите количество полученных базовых точек.
Пример 6. Изобразите на числовой окружности дуги, соответствующие числовым промежуткам.
Видео:Как решить пункт б) в задании 13 профиля ЕГЭ. ТригонометрияСкачать

Урок «Числовая окружность»
Краткое описание документа:
Видеоуроки относятся к наиболее эффективным средствам обучения, особенно таких школьных дисциплин, как математика. Поэтому автор данного материала собрал в единое целое только полезную, важную и грамотную информацию.
Данный урок рассчитан на 11:52 минут. Практически столько же времени требуется учителю на уроке для объяснения нового материала по данной теме. Хотя главным достоинством видеоурока будет тот факт, что обучающиеся будут внимательно слушать то, о чем говорит автор, не отвлекаясь на посторонние темы и разговоры. Ведь если обучающиеся будут слушать не внимательно, то упустят важный момент урока. А если материал будет объяснять учитель сам, то его обучающиеся смогут легко отвлечь от главного своими разговорами на отвлеченные темы. И, конечно, становится понятно, какой способ будет боле рационален.
Начало урока автор посвящает повторению тех функций, с которыми обучающиеся знакомились ранее в курсе алгебры. И первыми предлагается начать изучать – тригонометрические функции. Чтобы их рассматривать и изучать требуется новая математическая модель. И этой моделью становится числовая окружность, которая, как раз, и заявлена в теме урока. Для этого вводится понятие единичной окружности, задается ее определение. Далее на рисунке автор показывает все компоненты такой окружности, и что пригодится обучающимся для дальнейшего обучения. Дугами обозначаются четверти.
Затем автор предлагает рассмотреть числовую окружность. Здесь же он делает замечание, что удобнее использовать единичную окружность. На этой окружности показано, как получается точка M, если t>0, t 0(тэ больше нуля), то, двигаясь из точки А в направлении против часовой стрелки (положительное направление обхода окружности), опишем по окружности путь АМ (а эм) длины t. Точка М и будет искомой точкой М(t) (эм от тэ).
Видео:Вычисление значений тригонометрических функцийСкачать

Алгебра
План урока:
Видео:Решение тригонометрических уравнений. Подготовка к ЕГЭ | Математика TutorOnlineСкачать

Числовая и единичная окружность
В средней школе мы уже познакомились с координатной, или числовой прямой. Так называют абстрактную прямую, на которой выбрана точка отсчета, определен единичный отрезок, а также задано направление, в котором следует откладывать положительные числа. С помощью координатной прямой удается наглядно представлять сложение и вычитание как положительных, так и отрицательных чисел, решать задачи, связанные с перемещением по прямой, и делать многое другое.
Однако порою приходится рассматривать задачи, связанные с движением по окружности, а также складывать и вычитать углы. Здесь математикам помогает другая абстракция – числовая окружность. Пусть два гонщика (Вася и Петя) едут по круговой трассе, чья протяженность составляет 1 км. За минуту Вася проехал 1250 м, а Петя преодолел только 500 м. Попытаемся показать их положение графически.
Построим на координатной плоскости окружность с центром в начале координат длиной 1 км. Будем считать, старт находится в крайней правой точке трассы, на пересечении оси Ох и окружности. Также условимся, что гонщики едут против часовой стрелки. Тогда получим такую картинку:
Петя проедет ровно половину окружности и окажется в крайней левой точке трассы. Вася же за минуту успел сделать полный круг (1 км) и проехать ещё 250 м, а потому оказался в верхней точке.
Теперь предположим, что Петя стоит на месте, а Вася проехал ещё 250 м (четверть круга). В результате оба пилота оказались в одной точке, но проехали они разное расстояние! Получается, что по положению гонщика невозможно однозначно определить, сколько именно метров он проехал.
Заметим, что очень удобно характеризовать положение точки на числовой окружности с помощью угла. Достаточно соединить точку отрезком с началом координат. Полученный отрезок образует с прямой Ох некоторый угол α:
В тригонометрии предпочитают использовать особую числовую прямую, радиус которой равен единице. По ряду причин, которые станут ясны чуть позже, с ней очень удобно работать. Такую фигуру называют единичной окружностью.
Выглядит единичная окружность так:
Видео:Три способа отбора корней в задании 13 ЕГЭ профильСкачать

Откладывание углов на единичной окружности
Положение каждой точки на единичной окружности можно указать с помощью угла. Пусть надо найти точку, соответствующую углу 60°. Для этого просто строим угол следующим образом:
Углы, которые откладывают на единичной окружности, называют углами поворота. В данном случае можно утверждать, что точке А соответствует угол поворота, равный 60°.
Отложить можно и угол, больший 90° и даже 180°. Выглядеть они будут примерно так:
Углы можно складывать друг с другом и вычитать. Предположим, нам надо построить угол, равный сумме углов 120° и 110°. Для этого сначала совершить поворот на 120°, а потом от полученного отрезка отложить ещё один угол в 110°:
Ясно, что возможно построить любой угол в диапазоне от 0° до 360°. А можно ли отложить угол, который будет больше 360°? В обычной планиметрии мы не работаем с такими углами, однако в тригонометрии они существуют. Действительно, мы же можем, например, сложить углы 250° и 140°. В итоге получится 250 + 140 = 390°:
В результате мы совершили полный оборот (360°) и вдобавок повернули отрезок ещё на 30°. Получается, что углам в 390° и 30° соответствует одна и та же точка.
Углы можно и вычитать друг из друга. Для этого вычитаемый угол надо отложить в противоположном направлении – не против часовой, а по часовой стрелке. Например, вычитая из 150° угол в 70°, придем в точку, соответствующую 150 – 70 = 80°:
Из арифметики мы помним, что вычитание можно заменить прибавлением противоположного (то есть отрицательного) числа:
Получается, что отложив угол 70° по часовой стрелке, мы прибавили к 150° отрицательный угол (– 70°). То есть на единичной окружности можно откладывать отрицательные углы! Для их получения поворот надо осуществлять по часовой стрелке. Например, угол – 60° будет выглядеть так:
Итак, мы можем откладывать и положительные, и отрицательные углы, а также углы, большие 360°. Вообще в тригонометрии угол может быть равен любому действительному числу. На единичной окружности можно отложить углы величиной 1000°, 1000000° и (– 999999999°) и любые другие, самые большие и самые малые углы. В этом смысле единичная окружность схожа с координатной прямой. Разница лишь в том, что на прямой разным числам всегда соответствуют разные точки, а на окружности разным углам могут соответствовать одни и те же точки.
Ещё раз отметим, что один полный оборот равен 360°. Если отложить на окружности произвольную точку А, которой соответствует угол α, а потом добавить к α ещё 360°, то мы попадем в ту же самую точку:
С точки зрения тригонометрии те углы поворота, которые соответствуют одной точке на единичной окружности, равны друг другу. Поэтому можно записать формулу:
Естественно, при вычитании 360° из угла мы тоже совершим полный поворот, только по часовой стрелке, поэтому верна и другая запись:
Угол, не изменится и в том случае, если мы совершим не один, а два полных оборота, то есть добавим к нему 2•360° = 720°. Можно добавлять к углу два, три, четыре полных поворота, но он не изменится от этого. Обозначим буквой n количество оборотов, которые мы добавляем к углу. Естественно, что n – целое число. Справедливой будет формула:
Например, верны следующие равенства:
15° + 3•360° = 15° + 1080° = 1095°
100° + 10•360° = 100° + 3600° = 3700°
1000° = 1000° – 2•360° = 1000° – 720° = 280°
Очевидно, что любой точке на окружности соответствует какой-то угол α из промежутка 0 ≤ α 1 5
🔥 Видео
Координаты точек на числовой окружности, часть 5. Алгебра 10 класс.Скачать