Первая окружность с центром O, вписанная в равнобедренный треугольник KLM, касается боковой стороны KL в точке B, а основания ML — в точке A. Вторая окружность с центром O1 касается основания ML и продолжений боковых сторон.
а) Докажите, что треугольник OLO1 прямоугольный.
б) Найдите радиус второй окружности, если известно, что радиус первой равен 6 и AK = 16.
а) Пусть окружность с центром O1 касается продолжения боковой стороны KL в точке C. Центр окружности, вписанной в угол, лежит на его биссектрисе, поэтому LO и LO1 — биссектрисы смежных углов KLM и CLM. Следовательно, ∠OLO1 = 90°.
б) Прямоугольные треугольники KBO и KAL подобны, поэтому
Пусть радиус окружности с центром O1 равен r1. Треугольник KLM
равнобедренный, поэтому окружности с центрами O и O1 касаются основания ML в одной и той же точке A. Значит, точка A лежит на отрезке OO1, причём LA — высота прямоугольного треугольника OLO1, проведённая из вершины прямого угла. Следовательно,
| Критерии оценивания выполнения задания | Баллы |
|---|---|
| Имеется верное доказательство утверждения пункта a) и обоснованно получен верный ответ в пункте б) | 3 |
| Получен обоснованный ответ в пункте б) имеется верное доказательство утверждения пункта а) и при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | 2 |
| Имеется верное доказательство утверждения пункта а) при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки, обоснованно получен верный ответ в пункте б) с использованием утверждения пункта а), при этом пункт а) не выполнен | 1 |
| Решение не соответствует ни одному из критериев, приведённых выше | 0 |
| Максимальный балл | 3 |
Можно рассмотреть подобные треугольники и
Тогда
Видео:Окружность вписана в равнобедренный треугольник. Найти её радиус.Скачать

Решение №1380 Окружность, вписанная в равнобедренный треугольник АВС, касается его боковых сторон АВ и АС …
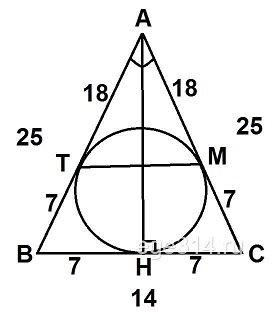
Окружность, вписанная в равнобедренный треугольник АВС, касается его боковых сторон АВ и АС в точках Т и М соответственно. Найдите ТМ, если АВ = 25, ВС = 14.
Источник задания: alexlarin.net
Проведём высоту АН:
В равнобедренном треугольнике высота является и медианой, которая делит ВС на две равные части:
ВН = НС = ВС/2 =14/2 = 7
Отрезки касательных к окружности, проведенных из одной точки, равны. Тогда:
ВН = ВТ = 7
СН = СМ = 7
Найдём АТ и АМ:
АТ = АВ – ВТ = 25 – 7 = 18
АС = АС – СА = 25 – 7 = 18
Треугольники АВС и АТМ подобны по двум пропорциональным сторонам и общему углу А. Составим соотношение сторон и найдём ТМ:
18·14 = 25·TM
252 = 25·TM
TM = 252/25 = 10,08
Видео:ЕГЭ Математика Задание 6#27935Скачать

Окружность, вписанная в равнобедренный треугольник $ABC$, касается боковой сторон…
Окружность, вписанная в равнобедренный треугольник $ABC$, касается боковой стороны в точке $K$ (см. рис.). Найдите длину отрезка $CK$, если известно, что периметр треугольника равен $36$ и основание $AB$ равно 10.
Объект авторского права ООО «Легион»
Видео:№691. Точка касания окружности, вписанной в равнобедренный треугольник, делит однуСкачать
Вместе с этой задачей также решают:
В параллелограмме $ABCD$ $AB = 6, AD = 9, sinA = /$. Найдите большую высоту параллелограмма.
Площадь треугольника ABC равна 76, DE — средняя линия, параллельная стороне AB. Найдите площадь трапеции ABED.
В параллелограмме $ABCD$ $AB = 12, AD = 16, sinA = /$. Найдите меньшую высоту параллелограмма.
Площадь параллелограмма ABCD равна 226. Точка P — середина стороны AD. Найдите площадь треугольника CDP.
🎦 Видео
Задача 6 №27934 ЕГЭ по математике. Урок 148Скачать

ОГЭ Задание 25 Демонстрационный вариант 2022, математикаСкачать
Вписанная и описанная около равнобедренного треугольника, окружностьСкачать

Геометрия Окружность, вписанная в равнобедренный треугольник, делит в точке касания одну из боковыхСкачать

Окружность вписанная в треугольник и описанная около треугольника.Скачать

Задание 16 ЕГЭ по математике #6Скачать
2083 окружность вписанная в равнобедренный треугольникСкачать

ОГЭ, геометрия, задачи повышенной сложности. Часть 3Скачать

ЕГЭ 2017 | Задание 3 | Окружность, вписанная ... ✘ Школа ПифагораСкачать

Демо ОГЭ по математике, задание 26Скачать

ОГЭ 2022 Демоверсия. 25 задание | Основание AC равнобедренного треугольника ABC равно 12.....Скачать

Задача 6 №27932 ЕГЭ по математике. Урок 146Скачать

Геометрия К окружности, вписанной в равнобедренный треугольник с основанием 12 см и высотой 8 смСкачать

14.36.1. Планиметрия. Гордин Р.К.Скачать

Вневписанная окружностьСкачать

Задание 26 Окружность Равнобедренный треугольникСкачать

Найти радиус равнобедренного прямоугольного треугольника 3 задание проф. ЕГЭ по математикеСкачать