Является ли овал окружностью (8 видео) | Курс школьной геометрии

Чем отличается эллипс от овала?

Чем отличается эллипс от овала? Данный вопрос часто остается без ответа — хоть эти две фигуры и знакомы всем еще со школьных времен. Но мало кто понимает, в чем разница между ними. И существуют ли вообще какие-либо отличия.

Содержание

В чем различие?
Построение овалов и эллипсов
Формулы и интересные факты
Окружность
Окружность и овал
Правило:
Окружность и круг
Диаметр и радиус
Разница между овалом и эллипсом
Определение
Сравнение
🌟 Видео

Видео:ПОСТРОЕНИЕ ОВАЛА │ КАК НАЧЕРТИТЬ ОВАЛ ПРИ ПОСТРОЕНИИ АКСОНОМЕТРИИ │ Урок #61Скачать

В чем различие?

Официальные определения каждой из фигур звучат достаточно сложно и непонятно.

Но, если откинуть заумные формулы и сложные определения — все намного проще.

Овал можно «растянуть» как угодно. Это может быть практически круг, либо узкая и длинная замкнутая кривая — главное, чтобы ее форма удовлетворяла определению.

Эллипс — это «правильный» овал. Его пропорции строго регламентированы. Длины осей должны соответствовать уравнению: a 2 =b 2 +c 2 .

Где а — это длинная полуось, b — короткая, а с — фокальное расстояние (от центра до фокуса).

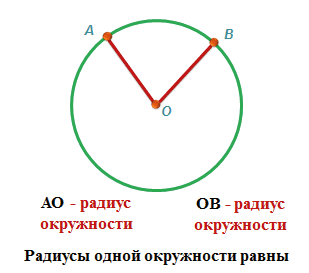
Всем известный круг — это частный вариант эллипса. В этом случае с=0 (т.к. фокус у него один). Полуоси (радиусы) тоже равны.

Видео:Как начертить овал во фронтальной плоскостиСкачать

Построение овалов и эллипсов

Казалось бы, а зачем их вообще строить?

Земная орбита имеет форму эллипса (траектории движения остальных планет и галактик аналогичны).

Практически в любой технике имеются круглые детали — а они при переведении в трехмерную проекцию будут изображаться в форме замкнутых кривых. Подобные примеры можно приводить бесконечно.

Поэтому в технике, космонавтике, астрономии, архитектуре и многих других научных отраслях разнообразные овалы приходится строить регулярно. Эти знания применяют даже люди, далекие от сложных вычислений — например, художники.

Для того чтобы начертить любую из этих фигур, потребуется лишь циркуль, транспортир и линейка. Сам процесс особых сложностей не вызывает, главное внимательность и точность.

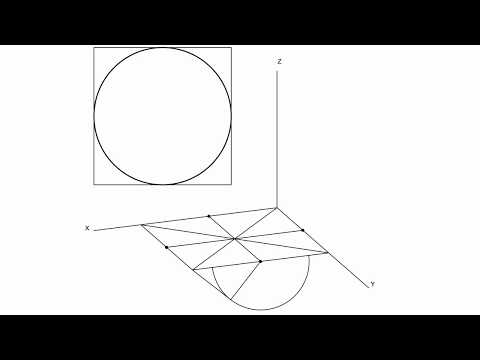
На фото ниже приведен пример построения эллипса в аксонометрии (изометрия).

Видео:Математика без Ху!ни. Кривые второго порядка. Эллипс.Скачать

Формулы и интересные факты

Хоть эти две фигуры и встречаются повсеместно, они до конца не изучены. В школьном курсе их проходят довольно поверхностно, не упоминая о возможных трудностях.

Овалы часто заменяют «правильными» эллипсами, так как с ними работать проще. Но даже в этом случае возникают сложности.

Так, казалось бы, простая задача — вычислить периметр — на самом деле невыполнима. Точной формулы не существует. Это связано с тем, что каждая точка имеет свой собственный радиус кривизны.

Школьникам и людям, далеким от точных вычислений, дают приблизительную формулу. Погрешность у такого результата будет велика, но для примитивных целей это допустимо.

В серьезных расчетах используются совсем другие формулы. Но даже они не дают желаемого результата, так как имеют достаточно большие отклонения от реальных значений.

Так, при расчете траектории движения космического корабля погрешность может достигать нескольких тысяч километров (на дальних расстояниях), а это слишком много. Поэтому поиски «идеальной» формулы ведутся до сих пор.

Видео:Всё про углы в окружности. Геометрия | МатематикаСкачать

Окружность

Приступаем к изучению окружности и круга. Вспомним замкнутые и незамкнутые линии. Познакомимся с центром окружности, радиусом и диаметром и научимся определять радиус при известном диаметре и диаметр при известном радиусе.

Окружность и овал

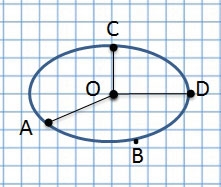
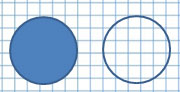
Для начала рассмотрим рисунок и найдём окружность:

Теперь рассмотрим сходства и различия этих геометрических фигур:

Центр в точке О

Есть точки A,B,C,D

Овал	Окружность

Сходства
Различия	В овале отрезки от точки O до крайней линии разные, а в окружности – все отрезки одинаковые.

Правило:

Окружность – это замкнутая кривая линия с точкой О в середине, которая называется центром.

Расстояния от центра до линии окружности одинаковые.

Начертить окружность можно при помощи циркуля:

А овал рисуют от руки:

Окружность и круг

Если заполнить пространство внутри окружности, то получим круг.

Круг – это часть плоскости, ограниченная окружностью.

Диаметр и радиус

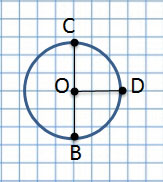
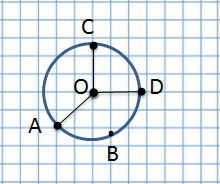
Если соединить центр окружности с линией окружности, получим радиус, например, OC, OA и OD.

Радиус – длина отрезка, соединяющего центр окружности с любой точкой, лежащей на окружности. Радиус составляет половину диаметра.

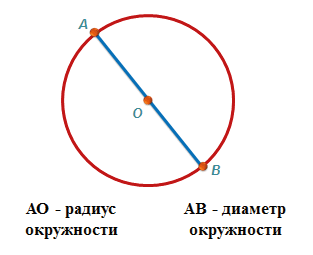
Если отрезок проходит через центр и соединяет две точки на окружности – это диаметр.

Диаметр – это длина отрезка, проходящего через центр окружности и соединяющего две точки на этой окружности.

Поделись с друзьями в социальных сетях:

Видео:Овал по заданным осям . Геометрические построения.Скачать

Разница между овалом и эллипсом

Простейшие математические термины могут вызвать настоящую головную боль у человека, далёкого от точных наук. Такие определения, как овал и эллипс, путают не только школьники, но и достаточно взрослые люди. Попробуем наметить отличия между данными понятиями, используя простые и доступные выражения, избегая математических терминов.

Видео:Изображение окружности в перспективе. Эллипс.Скачать

Определение

Овал – это замкнутая вытянутая геометрическая фигура, обладающая правильной формой и особыми свойствами. Вписанная в окружность, она обладает как минимум 4 точками экстремума, то есть вершинами. Если разделить овал прямой линией по двум противоположным вершинам, то два сегмента, полученные в результате данного действия, будут абсолютно идентичными.
Эллипс – это замкнутая плоская кривая, частный случай овала, у которого имеется 4 вершины в точках экстремума. Центральная ось, проведённая по двум противоположным точкам экстремума, содержит две точки фокуса, равноудалённые от вершин. Сумма расстояний от фокусов до любой точки на кривой эллипса – постоянная величина, которая равна длине центральной оси.

Эллипс к содержанию ↑

Видео:Как начертить овал. Эллипс вписанный в ромбСкачать

Сравнение

Таким образом, ключевое отличие между указанными понятиями на бытовом уровне улавливается через их определения. Вариантов построения овала – множество, оси, проведённые из точек их вершин, могут иметь различное соотношение. Если же мы говорим про эллипс, то здесь действуют особые условия его построения. На большей оси есть 2 фокуса, равноудалённые от вершин.

Сумма расстояний от фокусов до любой точки на кривой всегда одинаково и равно длине большой оси. Это свойство используют строители и дизайнеры для проецирования фигур на местности. Если же расстояние от фокусов будет одинаковым, но больше или меньше длины большой оси, то мы говорим об овале.