Волновой вектор как найти (3 видео) | Курс школьной геометрии

волновой вектор

ВОЛНОВОЙ ВЕКТОР — вектор k, определяющий направление распространения и пространственный период плоской монохроматич. волны

где — постоянные амплитуда и фаза волны, — круговая частота, r — радиус-вектор. Модуль В. в. наз. волновым числом k=, где — пространственный период или длина волны. В направлении В. в. происходит наибыстрейшее изменение фазы волны , поэтому оно и принимается за направление распространения. Скорость перемещения фазы в этом направлении, или фазовая скорость , определяется через волновое число . При классич. описании волновых процессов с В. в. связана плотность импульса , где — плотность энергии. В квантовом пределе соответственно импульс . Направление переноса энергии волной, вообще говоря, может и не совпадать с направлением В. в., как это имеет место, напр., в анизотропных средах или даже в изотропных средах с аномальной дисперсией, где возможен перенос энергии в направлении, противоположном В. в.

Понятие о В. в. может быть обобщено на случай квазигармонич. волн вида , если ввести локальный В. в. и мгновенную частоту . Однако, однозначная интерпретация этих величин допустима только при выполнении неравенств:

где k; — декартовы составляющие В. в. (i, j=1, 2, 3). Эти условия устанавливают применимость лучевого описания волновых процессов (приближения геометрической оптики и геометрической акустики, квазиклассич. приближения).

Для эл—магн. гармонической волны (в вакууме) В. в. k и величина (с — скорость света) объединяются в единый волновой четырёхвектор, компоненты к-рого подчиняются при переходе от одной инерциальной системы отсчёта к другой (движущейся с относит. скоростью u) Лоренца преобразованием:

Первое из этих соотношений определяет Доплера аффект, второе — эффект аберрации углов прихода волн (или формируемых ими лучей).

M. А. Миллер, Г. В. Пермитин.

Видео:Единичный векторСкачать

Волновой вектор как найти

Чтобы освободиться от использования системы координат запишем (см. Лекция 1, формула 15) с помощью векторных обозначений, полагая . Пусть вектор равен по модулю волновому числу и направлен параллельно оси в сторону положительных значений (рис. 1). Такой вектор называется волновым. Принимая во вниание, что , запишем для произвольной точки, характеризуемой радиусом-вектором , выражение

Рис. 1Рис. 2

Эта формула не зависит от системы координат и характеризует плоскую волну, распространяющуюся в направлении вектора .

Аналогичное выражение для волны можно также написать с использованием синуса:

которое при подходящем выборе начала отсчета времени может быть сведено к предыдущему, поскольку .

Представление плоской волны в комплексной форме . Принимая во внимание формулу Эйлера

представим выражения (1) и (2) формулами

где и — вещественная и мнимая части комплексного числа. В расчетах удобно пользоваться комплексным представлением плоской волны в виде

обозначая комплексную величину тем же символом, что и действительную. Это упрощает написание формул и не приводит к путанице. В тех случаях, когда путаница все же возможна, будем в явном виде указывать, о каком представлении идет речь.

Величина в (6) может быть как действительной, так и комплексной или мнимой. Учитывая, что в общем случае

запишем выражение (6) в виде

где — амплитуда плоской волны. Поэтому и в (7) — амплитуда плоской волны, а — фаза.

Будем искать решение уравнений Максвелла (см. Лекция 1, формула 2) и (см. Лекция 1, формула 3) в виде

где и — постоянные векторы, не зависящие от координат и времени. Компоненты этих векторов могут быть комплексными.

Подставляя выражения (8) в уравнения (см. Лекция 1, формула 2) и (см. Лекция 1, формула 3) и учитывая, что

получаем следующие соотношения:

Из соотношений (11) следует, что векторы и плоской волны перпендикулярны вектору , т. е. направлению распространения. Это означает, что электромагнитная волна является поперечной. Соотношения (10) показывают, что векторы и взаимно перпендикулярны. Таким образом, , и составляют тройку взаимно перпендикулярных векторов.

Поперечность световых колебаний была открыта в 1817г. Т.Юнгом (1773 — 1829). С помощью этого представления он объяснил отсутствие интерференции лучей света, поляризованных во взаимно перпендикулярных плоскостях, обнаруженное в 1816г. экспериментально в совместной работе Д.Ф.Араго (1786 — 1853) и О.Ж.Френеля (1788 — 1827).

Взяв от обеих частей второго уравнения (10) модули и учитывая, что , , находим следующее соотношение между напряженностью электрического поля и магнитной индукцией плоской волны в вакууме:

Поскольку в (10) — вещественные величины, из (8) заключаем, что и в плоской волне изменяются в одинаковой фазе, т. е. одновременно достигают максимальных и нулевых значений (рис. 2).

Видео:Орт вектора. Нормировать вектор. Найти единичный векторСкачать

ЭНЕРГИЯ ВОЛНЫ. ВЕКТОР УМОВА

ЛЕКЦИЯ №2

МЕХАНИЧЕСКИЕ ВОЛНЫ. АКУСТИКА

ОБЩИЕ ПОНЯТИЯ И ОПРЕДЕЛЕНИЯ

В широком смысле, под волной понимают процесс распространения в пространстве колебаний или возмущений состояния вещества или поля с течением времени. Математически этот процесс выражается функцией, описывающей распространение в пространстве изменений какой-либо физической величины. Выделяют три типа волн: волны на поверхности жидкости, упругие (иначе механические) и электромагнитные. Рассмотрим механические волны, т.е. процессы распространения механических возмущений в упругой среде.

Механические колебания, возбужденные в какой-либо точке пространства вследствие взаимодействия между упруго связанными частицами среды будут распространяться в ней с некоторой конечной скоростью. Частицы среды последовательно вовлекаются в колебательное движение около своих положений равновесия, но не перемещаются вместе с волной. Таким образом, в волновом процессе не происходит переноса массы. От частицы к частице передается только колебательное движение, а значит, и энергия.Перенос энергии без переноса вещества – это основное свойство всех волн, независимо от их природы.

Волны бывают продольные, если колебания частиц среды происходят вдоль направления распространения, и поперечные, если направление колебаний перпендикулярно вектору скорости волны. Очевидно, что в случае продольных волн в среде возникают деформации сжатия и разрежения, которые в свою очередь приводят к образованию локальных областей сгущения и разрежения вещества, т.е. области повышенного и пониженного давления. Такие волны могут возникать в любых средах: в газах, жидкостях и твердых телах. Поперечные механические волны обусловлены деформациями сдвига. Это означает, что они могут существовать только в твердых телах.

В общем случае, волны представляют собой пространственное образование. Геометрическое место точек (поверхность), до которых колебания дошли к некоторому моменту времени, называется фронтом волны. В зависимости от формы фронта волны бывают: плоские, сферические, цилиндрические и т.д.

Поверхность, точки которой имеют одно и то же значение фазы, называется волновой поверхностью. Волновых поверхностей

бесчисленное множество, а фронт волны всегда один.

УРАВНЕНИЕ БЕГУЩЕЙ ВОЛНЫ

Получим уравнение плоской волны в однородной среде вдоль оси 0х, совпадающей с направлением её распространения. Т.к., в этом случае фронт волны перпендикулярен 0х, то смещения s частиц среды будут зависеть только от координаты х и момента времени t, т.е. уравнение волны будет представлять собой функцию – s = f(x,t). Пред-положим, что в точке 0 (рис.1) частица совершает колебания по гармоническому закону: s = Acosωt. Тогда, очевидно, что колебания в некоторой точке М, удаленной от точки 0 на расстояние 0М = х, будут совершаться по тому же закону, но с некоторым отставанием по времени τ от колебаний в точке 0:

Если обозначить скорость волны через u, то время запаздывания, за которое волна добежит от точки 0 до точки М: τ = х/u, и уравнение колебаний в произвольной точке М на расстоянии х от источника примет вид:

s= A cos ω( t-τ ) = A cos ω( t — ). (2)

Это и есть искомое уравнение плоской бегущей волны. Здесь: А – амплитуда смещения частиц среды от положения равновесия, ω – циклическая частота колебаний частиц, ω( t — ) – фаза колебаний в точке с координатой х, u – скорость плоской волны.

Расстояние между ближайшими частицами среды, колеблющимися в одинаковой фазе, называется длиной волны λ (рис.1).

Длина волны равна расстоянию, на которое распространяется определенная фаза колебаний за период колебаний частиц среды. Тогда λ = u·T = u/ν. Т.к. ω = 2πν, то (2) можно переписать в виде:

s = Acosω( t — ) = Acos2π(vt — ) = Acos(ωt — 2π ). (3)

Покажем, что скорость распространения волны u – это скорость перемещения фиксированного значения фазы. Положим ω( t – ) = С, т.е. const. Выразим х: х = ut — Cu/ω. Продифференцировав это выражение по t, получим: (С, u, ω – величины постоянные для данной среды). Т.е. u – это скорость, с которой перемещается данное значение фазы. По этой причине скорость волны называют также фазовой скоростью.

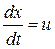
Скорость распространения механических волн зависит от физических свойств среды. Скорость распространения продольных волн определяется формулой: . Для поперечных волн – . Здесь r – плотность недеформированной среды, Е – модуль Юнга, G – модуль сдвига. Е и G – параметры упругости среды.

Основные свойства волн: прямолинейность распространения в однородной среде, отражение и преломление на границе раздела сред, дисперсия, интерференция и дифракция.

ВОЛНОВОЕ УРАВНЕНИЕ

Аналогично тому, как уравнение колебаний является решением дифференциального уравнения, описывающего процесс колебаний, так и уравнение волны представляет собой решение дифференциального уравнения, описывающего процесс распространения волн в среде. Это дифференциальное уравнение второго порядка в частных производных называется волновым. Найдем его вид. Запишем первые и вторые производные уравнения волны (2) по переменным t и х:

; ;

; ; (4)

; . (5)

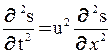
В трехмерном случае:

СТОЯЧИЕ ВОЛНЫ

Рассмотрим в качестве примера проявления волновых свойств механизм образования стоячих волн. Они возникают в результате наложения (интерференции) двух встречных плоских когерентных волн с одинаковой амплитудой. Например, волны падающей и этой же волны отраженной от границы раздела сред. Запишем уравнения двух плоских волн, движущихся навстречу друг другу в виде (3).

s ₁= Acos(ωt – 2π ) = А(cosωt cos2π + sinωt sin2π ) . (6)

s₂ = Acos(ωt + 2π ) = А(cosωt cos2π – sinωt sin2π ). (7)

Складывая эти равенства, получим уравнение результирующего процесса – уравнение стоячей волны:

(8)

Из (8) видно, что в каждой точке среды происходит колебание той же частоты ω, что и у интерферирующих волн. Однако амплитуда колебаний каждой частицы зависит от координаты точки среды, в которой она расположена: А_х = 2А cos2π . В точках, где аргумент 2π = ±nπ (при n = 0, 1, 2…) и |cos2π | = 1, амплитуда имеет максимальное значение –2А. Эти точки называются пучностями стоячей волны. В точках, где аргумент 2π = ±(n + )π, амплитуда минимальна и равна нулю, т.к. в этом случае cos2π = 0. Эти точки называются узлами стоячей волны.

На рис.2 показано как меняется расположение частиц среды в стоячей волне в течение периода.

ЭНЕРГИЯ ВОЛНЫ. ВЕКТОР УМОВА

Последовательное вовлечение в колебательное движение частиц среды означает, что волна передает от частицы к частице некоторую механическую энергию. Перенос энергии волнами количественно характеризуется вектором плотности потока энергии. Найдем выражение для энергии, переносимой плоской волной. Для этого рассмотрим некоторый объем V среды, все частицы которой вовлечены волной в колебательное движение (рис.3). В момент времени t каждая частица массой m₀ имеет определенные значения смещения и скорости. Однако, как мы установили ранее, полная механическая энергия частицы от этого не зависит и равна Е_м = , где m₀ – масса одной частицы. Полагая, что все частицы среды одинаковы, а их число в объеме V равно N, получим для энергии этого объема:

, (9)

где m = m₀·N масса вещества в объеме V. Разделив правую и левую часть этого равенства на V , получим количество энергии в единице объема волны. Эта величина называется объемной плотностью энергии:

, (10)

где ρ = m / V – плотность вещества среды, в которой распространяется волна. Объемная плотность энергии измеряется в Дж / м 3 .

Определим энергию, переносимую волной через площадку площадью S перпендикулярную 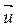(рис.3). За время t волна удалится от S на расстояние Δl = u·t и вовлечет в колебательное движение частицы в объеме V = S·u·t, перенеся при этом через площадку S энергию W = w∙V = w∙S∙ut.

Количество энергии, перенесенное через площадку S за единицу времени называется потоком энергии волны:

Ф = = w∙ S∙u. (11)

Поток энергии измеряется в Дж / с = Вт.

Количество энергии переносимое через единицу площади за единицу времени называется интенсивностью (или плотностью потока) энергии волны и измеряется в Вт / м 2 или Дж / (с·м 2 ):

. (12)

Т.к. скорость величина векторная, а w скалярная, то справа в этом равенстве стоит вектор. Это означает, что и левая величина дол-жна быть векторной, т.е. интенсивность энергии волны в направлении переноса – это некий вектор:

. (13)

Эта величина для упругих волн называется вектором Умова, который определяет количество энергии переносимое механической волной через единицу площади за единицу времени в направлении .

ЭФФЕКТ ДОПЛЕРА

Эффектом Доплера называют изменение частоты колебаний, воспринимаемых наблюдателем (приёмником волны) вследствие движения источника волны и наблюдателя относительно среды.

Рассмотрим простейший случай, когда источник волны и наблюдатель движутся вдоль соединяющей их прямой. Скорость распространения волны в рассматриваемой среде будем считать равной u, скорость источника – , скорость наблюдателя (приёмника) – , частота колебаний источника – ν_0, период колебаний источника – Т = 1/ ν₀. Все скорости определены относительно среды. Скорость источника будем считать положительной, если он движется по направлению к приёмнику, и отрицательной, если источник удаляется от приёмника. Аналогичное правило знаков скоростей примем и для приёмника.

В исходном состоянии источник находится в начале координат (точка 0), а приёмник в точке А. Скорость распространения колебаний зависит только от свойств среды, поэтому при неподвижном источнике за одну секунду волна пройдет в направлении к приемнику расстояние u. На этом расстоянии уложится ν₀ колебаний. Соответственно, длина волны – λ₀ = u / ν₀ (рис.4а).

Пусть наблюдатель неподвижен и находится на расстоянии u от источника, а источник волны движется с постоянной скоростью по направлению к наблюдателю. Будем считать, что