Рис. 1. Прямоугольный треугольник
Прямоугольный треугольник — треугольник, у которого один из углов прямой ( ).
Для нахождения параметров прямоугольного треугольника можно пользоваться тем, что он остаётся треугольником. Т.е. все формульные зависимости, характеризующие произвольный треугольник, применимы и для прямоугольного, однако то, что наш объект именно прямоугольный треугольник, даёт несколько новых возможностей для расчёта (рис. 1).
У такого треугольника вводятся собственные обозначения: так стороны, содержащие (примыкающие) к прямому углу, называются катетами ( и ), а сторона, находящаяся против угла в , называется гипотенузой ( ). Наиболее часто используемым соотношением для прямоугольного треугольника является теорема Пифагора, связывающая катеты треугольника с гипотенузой.
Кроме того, в данном треугольнике можно по-другому найти высоты, биссектрисы и медианы.
- биссектриса через гипотенузу и один из углов
- биссектриса через катет и один из углов
- биссектриса через катет и гипотенузу
- медиана через катеты (следствие т. Пифагора)
- медиана через катет и один из углов
- высота через гипотенузу и углы
Рис. 2. Прямоугольный треугольник (тригонометрия)
Кроме того, на основании прямоугольного треугольника вводятся понятия ряда тригонометрических функций (рис. 2)
- Синусом угла альфа ( ) называется отношение противолежащего катета к гипотенузе:
- Косинусом угла альфа ( ) называется отношение прилежащего катета к гипотенузе:
- Тангенсом угла альфа ( ) называется отношение противолежащего катета к прилежащему:
- Котангенсом угла альфа ( ) называется отношение прилежащего катета к противолежащему:
- Треугольник. Важные факты о высоте, биссектрисе и медиане
- Треугольник. Медиана, биссектриса, высота, средняя линия.
- теория по математике 📈 планиметрия
- Виды треугольников по углам
- Виды треугольников по сторонам
- Медиана, биссектриса, высота, средняя линия треугольника
- Медиана
- Биссектриса
- Высота
- Средняя линия
- 🌟 Видео
Видео:Геометрия 7 класс (Урок№12 - Медианы треугольника. Биссектрисы треугольника. Высоты треугольника.)Скачать

Треугольник. Важные факты о высоте, биссектрисе и медиане
Определения
Медиана треугольника – это отрезок, соединяющий вершину треугольника с серединой противоположной стороны.
Биссектриса треугольника – это отрезок биссектрисы угла треугольника, соединяющий вершину треугольника с точкой противоположной стороны.
Высота треугольника – это перпендикуляр, проведенный из вершины треугольника к прямой, содержащей противоположную сторону.
Теорема
В любом треугольнике высоты (или их продолжения) пересекаются в одной точке (рис. 1 и 2), биссектрисы пересекаются в одной точке (рис. 3), медианы пересекаются в одной точке (рис. 4).
Теорема
В равнобедренном треугольнике биссектриса, проведённая к основанию, является медианой и высотой.
Верны и другие утверждения:
В равнобедренном треугольнике высота, проведенная к основанию, является биссектрисой и медианой.
В равнобедренном треугольнике медиана, проведенная к основанию, является биссектрисой и высотой.
Теорема
В любом треугольнике медианы точкой пересечения делятся в отношении (2:1) , считая от вершины.
Доказательство
Пусть (AD) и (BE) – медианы в треугольнике (ABC) , (O) – точка пересечения (AD) и (BE) .
(DE) – средняя линия в треугольнике (ABC) , тогда (DEparallel AB) , значит (angle ADE = angle BAD) , (angle BED = angle ABE) , следовательно, треугольники (ABO) и (DOE) подобны (по двум углам).
Из подобия треугольников (ABO) и (DOE) : (dfrac = dfrac = dfrac) .
Для других медиан треугольника (ABC) требуемое свойство доказывается аналогично.
Теорема
Медиана треугольника делит его на два равновеликих треугольника (равновеликие треугольники – это треугольники, у которых площади равны).
Доказательство
Площадь треугольника равна половине произведения основания на высоту, проведенную к этому основанию: (S_ = 0,5cdot ACcdot h) .
Пусть (BD) – медиана в треугольнике (ABC) , тогда (AD = DC) .
(S_ = 0,5cdot ADcdot h) ,
(S_ = 0,5cdot DCcdot h) .
Так как (AD = DC) , то (S_ = S_) , что и требовалось доказать.
Теорема
В прямоугольном треугольнике медиана, проведенная к гипотенузе, равна половине гипотенузы.
Верно и обратное: если медиана равна половине стороны, к которой она проведена, то она проведена из вершины прямого угла.
Доказательство
1) Докажем, что если (triangle ABC) – прямоугольный, то (BM=frac12AC) , где (M) – середина гипотенузы (AC) .
Достроим треугольник (ABC) до прямоугольника (ABCD) и проведем диагональ (BD) . Т.к. в прямоугольнике диагонали делятся точкой пересечения пополам и равны, то (ACcap BD=M) , причем (AM=MC=BM=MD) , чтд.
2) Докажем, что если в треугольнике (ABC) медиана (BM=AM=MC) , то (angle B=90^circ) .
Треугольники (AMB) и (CMB) – равнобедренные, следовательно, (angle BAM=angle ABM=alpha, quad angle MBC=angle MCB=beta) .
Т.к. сумма углов в треугольнике равна (180^circ) , то для (triangle ABC) :
(alpha+(alpha+beta)+beta=180^circ Rightarrow alpha+beta=90^circ Rightarrow angle B=90^circ) , чтд.
Теорема
Биссектриса треугольника делит его сторону на части, пропорциональные прилежащим сторонам:
Верно и обратное: если отрезок, проведенный из вершины треугольника к стороне, делит эту сторону на отрезки, пропорциональные прилежащим сторонам, то это биссектриса.
Доказательство
Площади треугольников, у которых есть равные углы, относятся как произведения сторон, образующих эти углы, то есть [dfrac<S_><S_> = dfrac = dfrac]
В итоге (dfrac = dfrac<S_><S_> = dfrac) , откуда (dfrac = dfrac) , что и требовалось доказать.
Теорема
Если точка равноудалена от сторон угла, то она лежит на его биссектрисе.
Верно и обратное: если точка лежит на биссектрисе угла, то она равноудалена от его сторон.
Доказательство
1) Докажем, что если (KA=KB) , то (OK) – биссектриса.
Рассмотрим треугольники (AOK) и (BOK) : они равны по катету и гипотенузе, следовательно, (angle AOK=angle BOK) , чтд.
2) Докажем, что если (OK) – биссектриса, то (KA=KB) .
Аналогично треугольники (AOK) и (BOK) равны по гипотенузе и острому углу, следовательно, (KA=KB) , чтд.
Видео:Высота, биссектриса, медиана. 7 класс.Скачать

Треугольник. Медиана, биссектриса, высота, средняя линия.
теория по математике 📈 планиметрия
Треугольник – это геометрическая фигура, состоящая из трех точек на плоскости, которые не лежат на одной прямой, и трех последовательно соединяющих их отрезков.
Точки называют вершинами треугольника, а отрезки – сторонами. Вершины треугольника обозначают заглавными латинскими буквами.
Виды треугольников по углам
Треугольники классифицируются по углам: остроугольные; тупоугольные; прямоугольные.
| Остроугольные | Тупоугольные | Прямоугольные |
| Остроугольным треугольником называется треугольник, у которого все три угла острые. На рисунке показан такой остроугольный треугольник АВС. | Тупоугольным называется треугольник, у которого есть тупой угол. В треугольнике может быть только один тупой угол. На рисунке показан треугольник такого вида, где угол М – тупой. | Прямоугольным называется треугольник, у которого есть угол, равный 90 0 (прямой угол). На рисунке угол С равен 90 0 . Такой угол в любом прямоугольном треугольнике – единственный. |
 |  |  |
Виды треугольников по сторонам
Треугольники классифицируются по сторонам: разносторонний; равнобедренный; равносторонний.
| Разносторонний | Равнобедренный | Равносторонний |
| Треугольник называется разносторонним, если у него длины всех сторон разные. На рисунке показан такого вида треугольник АВС. | Треугольник называется равнобедренным, если у него две стороны равны. На рисунке показан равнобедренный треугольник АВС, у которого АВ=ВС. | Треугольник называется равносторонним, если у него все стороны равны. На рисунке показан такой треугольник, у него АВ=ВС=АС. |
 |  |  |
Видео:7 класс, 17 урок, Медианы, биссектрисы и высоты треугольникаСкачать

Медиана, биссектриса, высота, средняя линия треугольника
Медиана
Отрезок, соединяющий вершину треугольника с серединой противоположной стороны, называется медианой треугольника.
В любом треугольнике можно провести три медианы, так как сторон – три. На рисунке показаны медианы треугольника АВС: AF, EC, BD.
По данному рисунку также видно, что медианы треугольника пересекаются в одной точке – точке О. Это справедливо для любого треугольника.
Биссектриса
Биссектрисой треугольника называется луч, исходящий из вершины угла треугольника и делящий его пополам.
В любом треугольнике можно провести три биссектрисы, так как углов – три. На рисунке показаны биссектрисы треугольника ЕDC: DD1, EE1 и CC1.
По рисунку также видно, что биссектрисы имеют одну точку пересечения. Это справедливо для любого треугольника.
Высота
Высота треугольника – это перпендикуляр, проведенный из вершины треугольника к противоположной стороне.
На рисунке показаны высоты треугольника АВС: АН1, ВН2 и СН3.
По рисунку видно, что высоты треугольника пересекаются в одной точке. Это также справедливо для любого треугольника.
Средняя линия
Средней линией треугольника называется отрезок, соединяющий середины двух его сторон.
Средней линией треугольника называется отрезок, соединяющий середины двух его сторон. На рисунке показаны три средние линии треугольника АВС: MN, KN и MK.
Средняя линия обладает следующими свойствами: она параллельна противоположной стороне; она равна половине противоположной стороны. Так, на данном рисунке MN параллельна АС, KN параллельна АВ, MK параллельна ВС. Также MN=0,5АС, KN=0,5АВ и MK=0,5ВС. Например, если известно, что сторона АС=20 см, то средняя линия МN равна половине АС, то есть МN=10 см. Или, например, если средняя линия МК=12 см, то сторона ВС будет в два раза больше, то есть ВС=24 см.
Выполним чертеж окружности, описанной около треугольника АВС, покажем на нём все дополнительные элементы.
При построении прямой АО образовалась точка пересечения этой прямой с окружностью, обозначим её буквой Е и соединим с точкой В и с точкой С. Получим вписанные углы АВЕ и АСЕ, опирающиеся на диаметр АЕ, следовательно угол АВЕ и АСЕ равны по 90 0 .
Рассмотрим треугольники АВЕ и АВF: у них углы АВЕ и АFВ прямые, угол ЕАВ – общий, следовательно, эти треугольники подобны.
Составим отношение сторон:
A E A B . . = A B A F . . откуда по свойству пропорции АВ 2 =АЕ ∙ АF
Рассмотрим треугольники АСЕ и ADF, у которых углы АСЕ и AFD прямые, а угол FAD – общий. Значит, треугольники АСЕ и ADF подобны.
Составим отношение сторон:
A E A D . . = A C A F . . ; откуда выразим AD= A E ∙ A F А C . . = A E ∙ A F A C . .
Теперь рассмотрим наши два полученных равенства: АВ 2 =АЕ ∙ АF и AD= A E ∙ A F A C . .
Видим, что 36 2 =АЕ ∙ АF (подставили вместо АВ значение 36), также у нас известно, что АС=54. Найдем из второго равенства AD= A E ∙ A F A C . . = 36 2 54 . . = 24
Теперь найдем CD=AC-AD=54-24=30
pазбирался: Даниил Романович | обсудить разбор | оценить
На клетчатой бумаге с размером клетки 1х1 изображен треугольник АВС. Найти длину его средней линии, параллельной стороне АС.
Для решения задачи надо вспомнить свойство средней линии: она параллельна основанию и равна его половине. Следовательно, чтобы найти длину средней линии, надо сторону треугольника разделить пополам. Найдем сторону треугольника, которой параллельна средняя линия, т.е. АС, сосчитав клетки, получим, что АС равна 8. Значит, средняя линия равна 8:2=4.
pазбирался: Даниил Романович | обсудить разбор | оценить
В треугольнике АВС известно, что угол ВАС равен 84 0 , АD – биссектриса. Найдите угол ВАD. Ответ дайте в градусах.
Ключевое слово в данной задаче – биссектриса. Вспоминаем, что она делит угол пополам. Нам надо найти величину угла ВАD, следовательно он равен половине угла ВАС, то есть 84 0 :2=42 0
pазбирался: Даниил Романович | обсудить разбор | оценить
🌟 Видео
Высота медиана биссектриса в тупоугольном треугольникеСкачать

Медиана, биссектриса и высота. Прямоугольный треугольник.Скачать
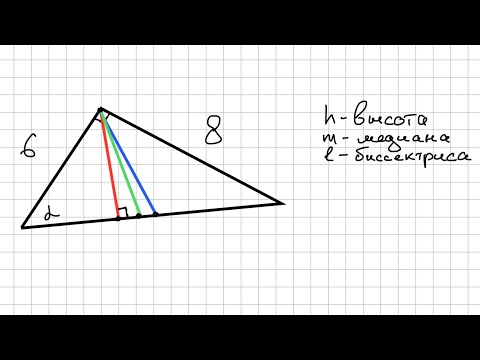
Построение медианы в треугольникеСкачать

Построение биссектрисы в треугольникеСкачать

Что такое медиана, биссектриса и высота?Скачать

Свойство биссектрисы треугольника с доказательствомСкачать

БИССЕКТРИСЫ, МЕДИАНЫ И ВЫСОТЫ В ПРЯМОУГОЛЬНЫХ ТРЕУГОЛЬНИКАХСкачать

Построение высоты в тупоугольном и прямоугольном треугольниках. 7 класс.Скачать

ГЕОМЕТРИЯ 7 класс. Медиана прямоугольного треугольника. Свойство. Доказательство для 7 класса.Скачать

ПРЯМОУГОЛЬНЫЙ ТРЕУГОЛЬНИК: высота, медиана, биссектрисаСкачать

БИССЕКТРИСА, МЕДИАНА, ВЫСОТА; Основные свойства (теория) | МатематикаСкачать

Построение высоты в треугольникеСкачать

Как найти длину биссектрисы, медианы и высоты? | Ботай со мной #031 | Борис ТрушинСкачать

КАК НАЙТИ ВЫСОТУ ТРЕУГОЛЬНИКА? ЕГЭ и ОГЭ #shorts #егэ #огэ #математика #профильныйегэ #треугольникСкачать

Высота, медиана, биссектриса треугольника. Как построить в треугольнике. Геометрия 7 классСкачать

Прямоугольный треугольник. Часть 3. Биссектриса | Борис Трушин #shortsСкачать

ЕГЭ 2024 по математике. №1,17 Медиана, биссектриса, высота, серединный перпендикулярСкачать

















