Векторы поля на границах раздела сред

Видео:2.5 Граничные условия для векторов поля на поверхности раздела средСкачать

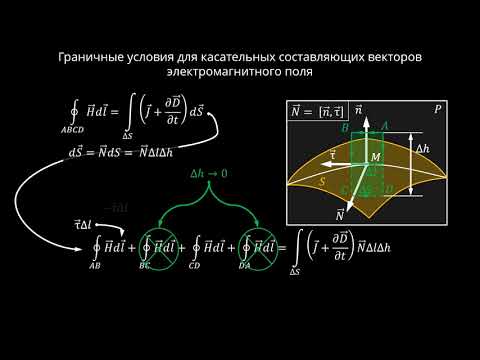
Общий подход к решению граничных задач

Основные понятия. Типичными для системы уравнений векторного поля являются задачи, в которых компоненты поля ищутся в бесконечной области, в то время, как причиной возникновения и поддержания состояния поля являются процессы, происходящие в конечной части пространства. При исследовании дифференциальных уравнений математической физики, с помощью которых описывается поле, в решения входят постоянные интегрирования их определяют с помощью граничных (краевых) условий. Таким образом, заданием только дифференциального уравнения, которому должно удовлетворять решение, задача определяется не однозначно, так как каждое уравнение, описывающее поле, имеет бесконечное число решений. Чтобы сделать задачу определенной, имеющей однозначный ответ, надо из всего множества возможных решений выбрать такое, которое обладает некоторыми свойствами на определенных граничных поверхностях. Любая физическая задача должна давать не только дифференциальное уравнение, которое надо решить, но также и граничные условия, которым должно удовлетворять решение. Поэтому под граничными следует понимать условия, которым подчиняется поле на границах раздела сред с различными свойствами.

Удовлетворить граничным условиям часто так же трудно, как и решить дифференциальное уравнение.

Первый факт, который надо заметить, состоит в том, что мы не можем пытаться подчинить решения данного уравнения граничным условиям произвольного вида. Для каждого типа уравнений имеется определенная совокупность граничных условий, определяющих ответ однозначно, в то время как при условиях другого вида ответ неоднозначен или невозможен. При этом, конечно, в реальной физической задаче граничные условия всегда должны быть правильного вида и определять ответ однозначно, и при постановке задачи в соответствии с реальной действительностью мы будем иметь всегда правильные граничные условия для уравнений. Однако не всегда легко сказать, какие именно граничные условия соответствуют «реальной действительности»; поэтому желательно знать, какие условия подходят для того или иного уравнения; это может дать указание, каким образом формулировать наши математические задачи, чтобы они возможно точнее соответствовали физическим.

Существует много разновидностей граничных условий, приемлемых при решении соответствующих полевых задач. Ниже рассмотрим граничные условия, с которыми приходится встречаться при расчёте электромагнитных полей.

Макроскопическое ЭМП в многосвязной неоднородной среде описывается системой дифференциальных уравнений Максвелла, дополненных системой материальных связей (п. 2.7). Уравнения Максвелла предполагают, что векторы ЭМП везде конечны, непрерывны и обладают необходимым количеством непрерывных производных. А для исключения многозначности поставленной задачи из всего многообразия возможных решений уравнений выбирается такое, которое обладает определенными начальными условиями и требуемыми свойствами на граничных поверхностях.

Под граничными условиями понимают условия, которым подчиняется поле на границах раздела сред с различными электромагнитными свойствами.

Из корпускулярной природы электричества и атомарной структуры поверхности раздела материальных сред следует, что поверхность раздела, вообще говоря, не является идеальной границей, а ЭМП в окрестности границы не является непрерывным и характеризуется большими градиентами поля. Несмотря на это, интегральные характеристики поля сохраняют свои значения по обе стороны от пограничного тонкого слоя, что позволяет при математическом моделировании заменять приграничную область идеальной поверхностью разрыва сред. При этом ЭМП в переходной области исключается из рассмотрения, а из законов формирования ЭМП в окрестности границы устанавливаются граничные условия для предельных значений векторов поля на идеальной поверхности разрыва сред. По существу, многообразие задач по расчету ЭМП в многосвязных областях определяется многообразием условий на границах раздела материальных сред.

Типичными для системы уравнений ЭМП являются задачи, в которых поле ищется в бесконечной области, в то время, как причиной возникновения и поддержания состояния поля являются процессы, происходящие в конечной части пространства. При исследовании дифференциальных уравнений математической физики, с помощью которых описываются ЭМП, в решения входят постоянные интегрирования. Пх определяют с помощью граничных условий.

При наличии в пространстве неоднородных поверхностей конечной толщины, разделяющих среды с различными свойствами, компоненты поля могут претерпевать резкий скачок при переходе через поверхность. В связи с этим при решении задач необходимо учитывать граничные эффекты, возникающие на поверхностях раздела сред. Математическое моделирование таких явлений сводится к замене неоднородных поверхностей идеальными поверхностями. При этом на идеальных поверхностях вводятся граничные условия, которым удовлетворяют предельные значения поля на соответствующих поверхностях.

Будем считать, что скачкообразный переход свойств одной среды в свойства другой является предельным случаем непрерывного перехода, при котором свойства одной среды переходят в свойства другой непрерывным образом в некоторой малой области, примыкающей к поверхности раздела. При этих предположениях для установления граничных условий необходимо учитывать уравнения Максвелла, которые выполнены также и в переходной области между двумя средами. В результате граничные условия являются прямым следствием уравнений Максвелла.

Видео:46. Граничные условия для электрического поляСкачать

Граничные условия для векторов электрического и магнитного поля на границе раздела двух сред

А) Граничные условия для вектора электрической индукции.

Рассмотрим границу раздела двух сред с различными диэлектрическими проницаемостями и . Выделим на границе элементарный цилиндр, как показано на рис. 3.1.1.

Рис.1.4.1.Элементарный цилиндр, выделенный на границе раздела двух сред для определения граничных условий на вектор электрической индукции. и — нормали к поверхности S.

Согласно теореме Гаусса-Остроградского поток вектора электрической индукции через замкнутую поверхность S равен алгебраической сумме зарядов внутри объема V, ограниченного этой поверхностью:

(3.1.1)

Устремим высоту цилиндра к нулю . Тогда (3.1.1) преобразуется так:

(3.1.2)

Где , – компоненты вектора индукции, перпендикулярные границе раздела, S — площадь основания цилиндра.

Введем поверхностную плотность заряда:

(3.1.3)

Размерность поверхностной плотности заряда = Кл/м2 (Кулон на квадратный метр).

Тогда (3.1.2) можно переписать в виде

(3.1.4)

Если плотность поверхностного заряда равна нулю (), то

. (3.1.5)

Мы можем сформулировать следующее важное утверждение:

На границе раздела, не содержащей поверхностных зарядов, нормальная составляющая вектора электрической индукции непрерывна.

Б) Граничные условия для вектора магнитной индукции.

Рассмотрим границу раздела двух сред, обладающих различной магнитной проницаемостью. Из тех же соображений, что и в предыдущем пункте и принимая во внимание, что магнитных зарядов не существует, можно записать

(3.1.6)

Это равенство равносильно следующему утверждению:

На границе раздела двух сред нормальная составляющая вектора магнитной индукции всегда непрерывна.

В) Граничные условия для вектора напряженности электрического поля .

Рассмотрим снова границу раздела двух сред с различными диэлектрическими проницаемостями и . Выделим на границе замкнутый контур в соответствии с рис. 3.1.2. и используем закон электромагнитной индукции:

Где L — выбранный контур, L = 2 (1 + ) , S — площадь поверхности, ограниченная контуром L.

Рис.3.1.2. Контур на границе раздела двух сред, используемый при определении граничных условий для векторов напряженности электрического поля.

Устремим ширину контура к нулю, тогда поток вектора через поверхность S обратится в ноль, и мы получим

(3.1.7)

Откуда следует, что

(3.1.8)

Это равенство равносильно следующему утверждению:

На границе раздела двух сред касательная составляющая вектора напряженности электрического поля всегда непрерывна.

Г) Граничные условия для вектора напряженности магнитного поля Н.

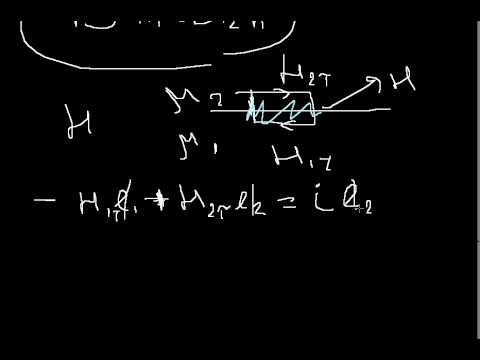
Как в предыдущем случае выделим на границе раздела двух сред замкнутый контур L (рис.1.4.2). Воспользуемся законом полного тока

(3.1.9)

Где — плотность тока, протекающего через поверхность S, ограниченную контуром L.

Учтем, что вдоль границы раздела может течь ток проводимости, тогда при стремлении следует ввести поверхностную плотность тока:

(3.1.10)

Размерность поверхностной плотности тока [] = А/м. Теперь (3.1.9) можно переписать так:

Откуда следует, что

(3.1.11)

Это равенство равносильно следующему утверждению:

На границе раздела двух сред разность касательных составляющих напряженности магнитного поля равна поверхностной плотности тока.

При отсутствии поверхностного тока

(3.1.12)

Это равенство равносильно следующему утверждению:

На границе раздела двух сред, по которой не течет поверхностный ток, касательная составляющая магнитного поля непрерывна.

Д) Граничные условия на поверхности идеального проводника.

Определим идеальный проводник, как проводник, внутрь которого не может проникать электромагнитное поле . Для полей СВЧ-диапазона хорошие проводники (серебро, медь) можно в первом приближении рассматривать как идеальные. На поверхности такого проводника, тем не менее, может течь ток проводимости и формироваться поверхностный заряд. Поэтому на поверхности идеального проводника

, ,

, .

Силовые линии электрического поля перпендикулярны к поверхности идеального проводника; силовые линии магнитного поля касательны к поверхности идеального проводника, как показано на рис.3.1.3.

Рис.3.1.3. Силовые линии электрического и магнитного полей вблизи поверхности идеального проводника.

Видео:Лекция 4-2. Условия на границе раздела двух диэлектриковСкачать

Взаимодействие света с границей раздела сред. Формулы Френеля

1. Поляризация света – это одно из фундаментальных свойств электромагнитного излучения. Оно состоит в неравноправности различных направлений в плоскости, перпендикулярной световому лучу. Поляризация присуща только поперечным волнам.

В электромагнитной теории света поперечность, а, следовательно, поляризованность световых волн вытекает с очевидностью. Но в эфирной волновой модели света, развивавшейся до конца XIX века, поперечность световых волн потребовала специальных доказательств. В таких явлениях, как интерференция и дифракция, вопрос о характере упругих колебаний не имеет принципиального значения. Оба эти явления реализуются как в случаях поперечных (свет), так и в случае продольных (звук) волн.

Термин «поляризация света» (от греческого polos – ось, полюс) предложил в 1808 г. Этьен Малюс.

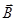
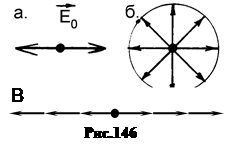
Поперечность световых волн выражается в том, что колеблющиеся в них векторы напряженности электрического поля Е и индукции магнитного поля перпендикулярны направлению распространения волны.

Естественный свет, излучаемый любым естественным источником, не поляризован. Хотя каждый элементарный цуг, излучаемый атомом, поляризован, плоскости поляризации разных цугов (плоскости колебаний Е) хаотично ориентированы в пространстве (рис.146 а и б).

Для того, чтобы получить пучок света, плоскости поляризации цугов в котором совпадают (рис.146-в) в оптике используются два способа: взаимодействие световых волн с границей раздела сред и взаимодействие света с анизотропной средой – кристаллом.

В настоящем параграфе будет рассмотрен первый способ, основанный на взаимодействии электромагнитной волны с границей раздела сред. Это взаимодействие зависит от того, как расположена относительно плоскости падения плоскость колебаний вектора E волны. Выделим и рассмотрим здесь два случая:

а. Плоскость колебаний вектора E лежит в плоскости падения;

б. Плоскость колебаний вектора E лежит перпендикулярно плоскости падения.

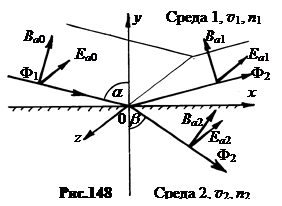
2. Взаимодействие с границей раздела изотропных сред электромагнитной волны, вектор Е которой колеблется в плоскости падения. Напомним, что плоскость падения – это плоскость, в которой лежат падающий, отраженный, преломленный лучи и перпендикуляр, восстановленный в точку падения.

Пусть в точку О на границе раздела сред падает поляризованная электромагнитная волна, вектор Е которой колеблется в плоскости падения (рис.147). Обозначим амплитудные значения вектора напряженности электрического поля: падающей (E_a0), отраженной (E_a1) и преломленной (E_a2) волн. Полагаем, что свет не поглощается веществом сред. Как известно из курса электричества, касательная составляющая вектора напряженности электрического поля E на границе диэлектрических сред не испытывает разрыва, а нормальная составляющая терпит разрыв, подчиняющийся условию: e₁E_n1 = e₂E_n2. Здесь e₁ и e₂— диэлектрические проницаемости сред.

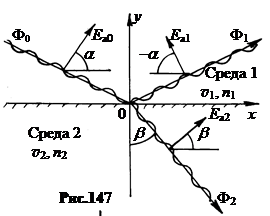
Отсюда можно получить два уравнения.

Для касательных составляющих: 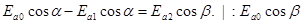. (17.1)

Сумма касательных составляющих векторов E_a0 и E_a1 в среде 1 равна касательной составляющей вектора E_a2 в среде 2.

Для нормальных составляющих: 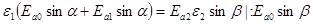. (17.2)

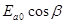
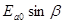
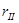
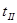
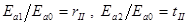
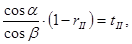
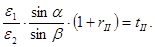
Разделим первое уравнение на , а второе на . Коэффициенты отражения и пропускания электромагнитной волны по амплитуде обозначим соответственно и : . Получаем: (17.3, 17.4)

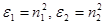
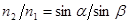
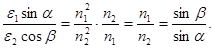
Так как , и , то коэффициент перед скобкой во втором уравнении принимает вид: (17.5)

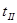
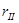
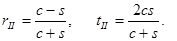
Перепишем систему с преобразованным вторым уравнением и, разрешив ее относительно и , получим (17.6)

Здесь 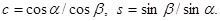(17.7)

Если использовать тригонометрические тождества, то формулы можно записать более компактно: 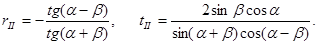(17.8)

В таком виде эти формулы получил впервые Огюст Френель в 1821 году. Он решил данную задачу в эфирной модели, в которой свет понимается как звуковая (механическая) волна в упругом эфире. Удивительно, что электромагнитная теория света сохранила вид формул (17.8), которые называют формулами Френеля.

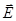
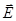
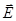
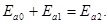
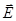
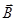
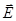
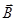
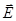
3. Взаимодействие с границей раздела изотропных сред электромагнитной волны, векторEкоторой колеблется в плоскости, перпендикулярной плоскости падения. В этом случае на границе раздела сред вектор имеетлишь одну составляющую, которая параллельна границе и противоположна оси OZ (рис.148). Составляющие вектора по осям OX и OY равны нулю. Для непрерывной касательной составляющей вектора имеем уравнение: (17.11)

Для нормальной составляющей вектора уравнения нет. Поэтому воспользуемся магнитным полем волны. Вектор индукции в данном случае расположен точно так же, как вектор в предыдущем случае. Поэтому условие непрерывности касательной составляющей вектора записывается так же, как для вектора в предыдущем случае (формула 17.1). B_a0cosa – B_a1cosa = B_a2cosb (17.12)

Перейдем в уравнении (17.12) от В к Е, используя связь между этими величинами. Так как B 2 ½mm₀ = ee₀E 2 , то (17.13)

Но — константа, — показатель преломления среды. Сократив все члены второго уравнения на с, получаем систему:

Обозначив получаем :

(17.16)

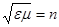
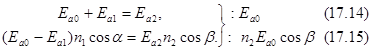
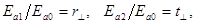
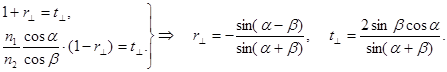
Выражения для 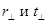так же совпали с результатами Френеля и тоже называются формулами Френеля.

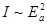
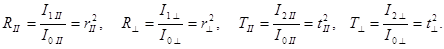
4. Коэффициенты отражения и пропускания по интенсивности. Так как интенсивность света I пропорциональна квадрату амплитуды, , то коэффициенты по интенсивности равны квадрату соответствующего коэффициента по амплитуде.

(17.17)

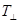
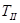
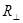
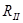
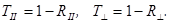
Коэффициенты пропускания по интенсивности и выразим через коэффициенты отражения и , исходя из закона сохранения энергии (17.18)

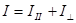
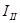
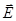
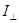
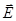
При падении на границу раздела двух сред неполяризованного света его интенсив-ность I может быть представлена как сума интенсивностей двух его компонент, . Здесь — интенсивность компоненты, вектор которой колеблется в плоскости падения, — интенсивность компоненты, вектор которой перпендикулярен плоскости падения.

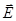
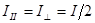
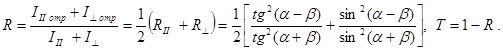
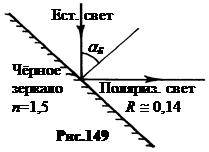
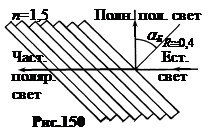
В силу случайной ориентации плоскостей колебании отдельных цугов обе этих компоненты равноправны, . Отсюда можно найти суммарный коэффициент отражения по интенсивности неполяризованной волны, падающей на границу раздела сред. (17.19), (17.20)

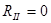
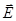
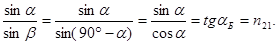
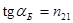
5. Закон Брюстера. Если a + b = 90°, то tg(a + b) = ∞, а . Следовательно, если луч естественного света падает на границу раздела сред под углом a = 90°– b, то в отражен-ном луче будут присутствовать только те волны, вектор которых перпендикулярен плоскости падения и отражаться будет полностью поляризованная волна. Угол полной поляризации из закона преломления. (17.21)

Угол падения, при котором отраженный от диэлектрика свет полностью поляризован, открыл экспериментально в 1815 году Дэйвид Брюстер. Поэтому формулу называют законом Брюстера, а угол полной поляризации a_Б– углом Брюстера.

6. Поляризаторы– это устройства, позволяющие выделить из пучка естественного света поляризованную в одной плоскости компоненту.

R@0,45В качестве поляризатора может использоваться обычная стеклянная пластина, на которую свет падает под углом Брюстера (рис 149). Это так называемое зеркало Малюса. Недостаток зеркала Малюса – низкая интенсивность отраженного поляризованного пучка.

Для увеличения светосилы поляризатора А. Столетов предложил использовать в качестве зеркала Малюса не черное, а прозрачное стекло, складывая несколько пластинок в стопу (рис 150). Поскольку толщина пластинок много больше длины когерентности естественного света, то отраженные от пластинок лучи не интерферируют, а их интенсивности просто складываются. За счет этого коэффициент отражения стопы Столетова приближается к 50%.

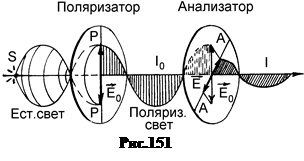
7. Закон Малюса. Чтобы убедится в том, что свет поляризован, нужно на его пути поставить второй поляризатор, называемый в этом качестве анализатором (рис.151).

В 1810 году Этьен Малюс нашел закон изменения интенсивности линейно поляризованного света после его прохождения через анализатор. I = I₀cos 2 j. (17.22)

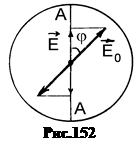
Здесь I₀ — интенсивность линейно поляризованного света, падающего на анализатор, j – угол между плоскостью поляризации света, падающего на анализатор, и плоскостью пропускания анализатора.

Закон Малюса вытекает из того, что через анализатор проходит составляющая вектора E₀ падающей волны, приходящейся на плоскость пропускания анализатора АА (рис.152). Очевидно, E = E₀cosj. Но интенсивность света пропорциональна квадрату амплитуды вектора E. Следовательно: I₀ = kE₀ 2 , I = kE 2 = kE₀ 2 cos 2 j = I₀cos 2 j. Здесь k – коэффициент пропорциональности.

8. Отражение нормально падающих на поверхность лучей. При проектировании оптических приборов важно знать коэффициент отражения падающих нормально границе раздела сред лучей. Подстановка a = b = 0приводит в формулах Френеля к неопределенности 0/0. Поэтому преобразуем формулу для R (17.20) к малым углам a и b, близким к нулю.

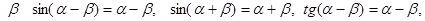
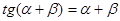
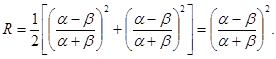
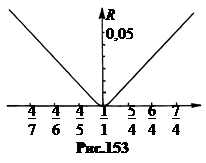
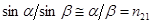
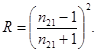
При малых a и . Отсюда: (17.23)

Т.к. , b = açn₁₂, (17.24)

Кривая зависимости коэффициента отражения света R от границы раздела сред симметрична относительно ординаты, соответствующей n₂çn₁ = 1 (рис.153). Это значит, что коэффициент отражения не зависит от того, с какой стороны падает на границу свет.

Чем больше отношение n₂çn₁, то есть чем сильнее отличаются среды, тем больше коэффициент отражения R. С ростом показателя преломления диэлектрика коэффициент отражения лучей от их поверхности, граничащей с воздухом, растет. От стекла с n = 1,5 отражается 4 % энергии падающих лучей, а от алмаза с n = 2,4 отражается 17 %. Сквозь двухлинзовый объектив, изготовленный из тяжелого флинта с n = 1,75, проходит всего лишь 70 % падающего света. Отсюда становится понятно, как велико положительное значение просветляющих покрытий.

С увеличением угла падения лучей a коэффициент отражения монотонно растет от минимального значения, соответствующего нормальному падению лучей (формула 17.24) до 1 при a = 90° (рис.154). Поэтому зеркальные отражения низких берегов в спокойных водоемах почти так же ярки, как сами берега. Отражение в воде заходящего солнца так же почти не уступает по яркости самому солнцу.

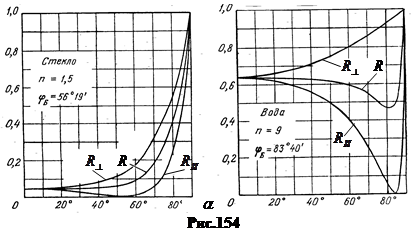
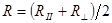
На рисунке 154 слева показаны теоретические кривые для коэффициентов отражения видимого света от стекла (n = 1,5), а справа – от воды ( 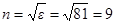). Внизу на графиках указанны углы a падения луча в градусах.

🎬 Видео

Билет №06-08 "Диэлектрики"Скачать

магнитная защита. Векторы B и H на границе разделаСкачать

Поток вектора напряженности электрического поля. Теорема Гаусса. 10 класс.Скачать

1.1 Векторы напряженности и индукции электрического и магнитного полейСкачать

Урок 228. Диэлектрики в электрическом поле. Диэлектрическая проницаемостьСкачать

44. Электрическое поле в диэлектрике. Вектор поляризованностиСкачать

1.2 Материальные уравнения, векторы поляризованности и намагниченности средСкачать

Билеты №18 и 19 "Теорема о циркуляции магнитного поля. Граничные условия"Скачать

ЧК_МИФ (ЛИКБЕЗ) 3_2_1 ПРОХОЖДЕНИЕ СВЕТА ЧЕРЕЗ ГРАНИЦУ РАЗДЕЛА ДВУХ СРЕД -1 (Минимум теории)Скачать

Урок 289. Магнитное поле в веществе. Магнитная проницаемость. Диа-, пара- и ферромагнетикиСкачать

Модуль 1 Лекция 3 Поляризация волн, явления на границе раздела средСкачать

Урок 222. Поток вектора напряженности электрического поляСкачать

Урок 218. Напряженность электрического поляСкачать

граница раздела двух диэлектриков 2Скачать

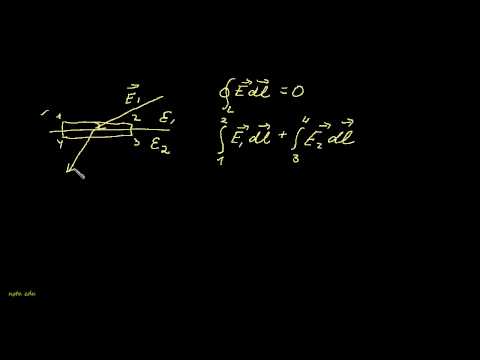
Билет №02 "Теорема Гаусса"Скачать

Поток вектора напряженности электрического поля. Теорема Гаусса. Практическая часть. 10 класс.Скачать

Модуль 1 Лекция 3 Поляризация волн, явления на границе раздела сред новСкачать