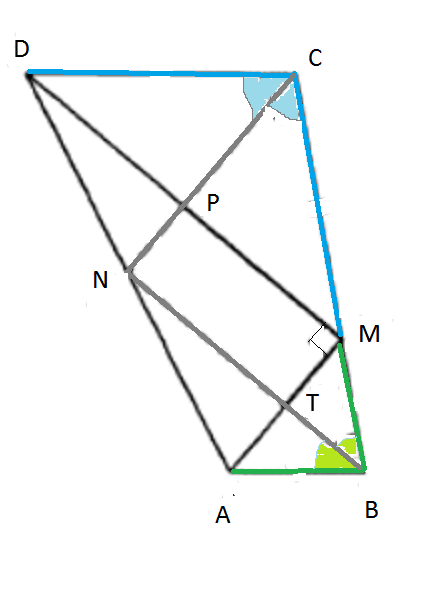
Точка M лежит на стороне BC выпуклого четырёхугольника ABCD, причём B и C — вершины равнобедренных треугольников с основаниями AM и DM соответственно, а прямые AM и MD перпендикулярны.
а) Докажите, что биссектрисы углов при вершинах B и C четырёхугольника ABCD, пересекаются на стороне AD.
б) Пусть N — точка пересечения этих биссектрис. Найдите площадь четырёхугольника ABCD, если известно, что BM : MC = 3 : 4, а площадь четырёхугольника, стороны которого лежат на прямых AM, DM, BN и CN, равна 24.
а) Пусть K — середина отрезка AM. Треугольник AMB равнобедренный, поэтому отрезок BK является в нём медианой, биссектрисой и высотой. Поскольку прямые DM и AM перпендикулярны, прямая KB|| MD и содержит среднюю линию треугольника AMD, то есть проходит через середину стороны AD. Аналогично, биссектриса угла MCD тоже проходит через середину стороны AD. Следовательно, биссектрисы углов B и C четырёхугольника ABCD пересекаются на стороне AD.
б) Пусть прямые AM и BN пересекаются в точке K, а прямые DM и CN — в точке L. Тогда четырёхугольник KMLN — прямоугольник.
Аналогично,
| Критерии оценивания выполнения задания | Баллы |
|---|---|
| Имеется верное доказательство утверждения пункта a) и обоснованно получен верный ответ в пункте б) | 3 |
| Получен обоснованный ответ в пункте б) имеется верное доказательство утверждения пункта а) и при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | 2 |
| Имеется верное доказательство утверждения пункта а) при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки, Содержание Видео:№783. Точка М лежит на стороне ВС параллелограмма ABCD, причем ВМ:МС=3:1. ВыразитеСкачать  В выпуклом четырехугольнике abcd точка m лежит на стороне bcБАЗА ЗАДАНИЙ Задание № 16. Планиметрия с доказательством. 1. Прямая, проходящая через вершину B прямоугольника ABCD перпендикулярно диагонали AC, пересекает сторону AD в точке M, равноудалённой от вершин B и D. 2. К окружности, вписанной в квадрат ABCD, проведена касательная, пересекающая стороны AB и AD в точках M и N соответственно. 3. Диагонали AC и BD четырёхугольника ABCD, вписанного в окружность, пересекаются в точке P, причём BC=CD. 4. В треугольнике ABC точки A 1 , B 1 , C 1 — середины сторон BC, AC и A B соответственно, AH— высота, ∠BAC = 60°, ∠BCA = 45°. 5. Две окружности касаются внутренним образом в точке A, причём меньшая проходит через центр большей. Хорда BC большей окружности касается меньшей в точке P. Хорды AB и AC пересекают меньшую окружность в точках K и M соответственно. 6. Две окружности касаются внутренним образом в точке A, причём меньшая окружность проходит через центр O большей. Диаметр BC большей окружности вторично пересекает меньшую окружность в точке M, отличной от A. Лучи AO и AM вторично пересекают большую окружность в точках P и Q соответственно. Точка C лежит на дуге AQ большей окружности, не содержащей точку P. 7. Две окружности касаются внутренним образом в точке K, причём меньшая проходит через центр большей. Хорда MN большей окружности касается меньшей в точке C. Хорды KM и KN пересекают меньшую окружность в точках A и B соответственно, а отрезки KC и AB пересекаются в точке L. 8. Дан прямоугольный треугольник ABC с прямым углом C. На катете AC взята точка M. Окружность с центром O и диаметром CM касается гипотенузы в точке N. 9. Точка B лежит на отрезке AC. Прямая, проходящая через точку A, касается окружности с диаметром BC в точке M и второй раз пересекает окружность с диаметром AB в точке K. Продолжение отрезка MB пересекает окружность с диаметром AB в точке D. 10. Точка M лежит на стороне BC выпуклого четырёхугольника ABCD, причём B и C — вершины равнобедренных треугольников с основаниями AM и DM соответственно, а прямые AM и MD перпендикулярны. 11. В равнобедренном тупоугольном треугольнике ABC на продолжение боковой стороны BC опущена высота AH. Из точки H на сторону AB и основание AC опущены перпендикуляры HK и HM соответственно. 12. Точка O — центр окружности, описанной около остроугольного треугольника ABC, I — центр вписанной в него окружности, H — точка пересечения высот. Известно, что ∠BAC = ∠OBC+∠OCB. 13. Точки P, Q, W делят стороны выпуклого четырёхугольника ABCD в отношении AP:PB = CQ:QB = CW:WD = 3:4, радиус окружности, описанной около треугольника PQW, равен 10, PQ = 16, QW = 12, угол PWQ— острый. 14. Окружность проходит через вершины В и С треугольника АВС и пересекает АВ и АС в точках C 1 , B 1 соответственно. 15. Дана трапеция ABCD с основаниями AD и BC. Диагональ BD разбивает её на два равнобедренных треугольника с основаниями AD и CD. 16. В прямоугольном треугольнике АВС с прямым углом С точки М и N – середины катетов АС и ВС соответственно, СН – высота. 17. В треугольнике АВС угол АВС равен 60°. Окружность, вписанная в треугольник, касается стороны AC в точке M. 18. В треугольнике АВС проведены высоты АК и СМ. На них из точек М и К опущены перпендикуляры МЕ и КН соответственно. 19. Окружность, вписанная в треугольник KLM, касается сторон KL, LM, MK в точках A, B и C соответственно. б) Найдите отношение LB:BM, если известно, что KC:CM = 3:2 и ∠ MKL = 60. 20. Дана равнобедренная трапеция ABCD с основаниями AD и BC. Окружность с центром O, построенная на боковой стороне AB как на диаметре, касается боковой стороны CD и второй раз пересекает большее основание AD в точке H, точка Q — середина CD. 21. Квадрат ABCD вписан в окружность. Хорда CE пересекает его диагональ BD в точке K. 22. В прямоугольном треугольнике ABC точки M и N – середины гипотенузы AB и катета BC соответственно. Биссектриса ∠ BAC пересекает прямую MN в точке L 23. Окружность касается стороны AC остроугольного треугольника ABC и делит каждую из сторон AB и BC на три равные части. 24. На катетах AC и BC прямоугольного треугольника ABC как на диаметрах построены окружности, второй раз пересекающиеся в точке M. Точка Q лежит на меньшей дуге MB окружности с диаметром BC. Прямая CQ второй раз пересекает окружность с диаметром AC в точке P. 25. Окружность, построенная на медиане BM равнобедренного треугольника ABC как на диаметре, второй раз пересекает основание BC в точке K. 26. В прямоугольной трапеции ABCD с прямым углом при вершине A расположены две окружности. Одна из них касается боковых сторон и большего основания AD, вторая – боковых сторон, меньшего основания BC и первой окружности. 27. В трапецию ABCD с основаниями AD и BC вписана окружность с центром O. 28. Дана трапеция с диагоналями равными 8 и 15. Сумма оснований равна 17. Видео:🔴 В выпуклом четырёхугольнике ABCD известно ... | ЕГЭ БАЗА 2018 | ЗАДАНИЕ 15 | ШКОЛА ПИФАГОРАСкачать  Задача 12101 Точка M лежит на стороне BC выпуклого.УсловиеТочка M лежит на стороне BC выпуклого четырёхугольника ABCD, причём B и C — вершины равнобедренных треугольников с основаниями AM и DM соответственно, а прямые AM и MD перпендикулярны. а) Докажите, что биссектрисы углов при вершинах B и C четырёхугольника ABCD пересекаются на стороне AD. б) Пусть N — точка пересечения этих биссектрис. Найдите площадь четырёхугольника ABCD, если известно, что BM:MC=1:3, а площадь четырёхугольника, стороны которого лежат на прямых AM, DM, BN и CN, равна 18. РешениеПусть Т- середина АМ. Треугольник АМВ — равнобедренный, значит ВТ- высота, медиана и биссектриса. NPMT- прямоугольник. Так как ВМ:МС=1:3, то BT:NT=1:3 и MT:PC=1:3 S(ΔABM)=BT*AM/2=BT*TM=(NT/3)*TM=S(NPTM)/3=18/3=6 S(ABCD)=S(ΔDMA)+S(ΔAMB)+S(ΔDMC)=36+6+54=96 🔥 ВидеоГеометрия В выпуклом четырёхугольнике ABCD известны стороны и диагональ: AB = 3, BC = CD = 5, AD = 8Скачать  ОГЭ без рекламы математика 11 и 12 вариант задача 25Скачать  В выпуклом четырёхугольнике ABCD AB=BC ... | ОГЭ 2017 | ЗАДАНИЕ 11 | ШКОЛА ПИФАГОРАСкачать  ОГЭ 2024 Ященко 3 вариант ФИПИ школе полный разбор!Скачать  Задача№25 ОГЭ Точка M и N лежат на стороне АС. Найдите радиус окружности, если cos ВАС ...Скачать  9 класс. Геометрия. ОГЭ. Окружность. Четырехугольники.Скачать  ОГЭ 2024 Ященко 4 вариант ФИПИ школе полный разбор!Скачать  ОГЭ Задание 26 Теорема косинусовСкачать 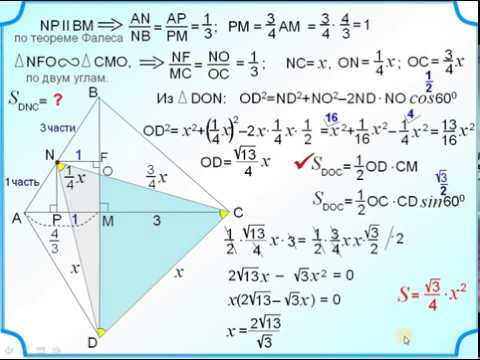 №47. В пространственном четырехугольнике ABCD стороны АВ и CD равны. Докажите, что прямые АВ и CDСкачать  ОГЭ Задание 24 Площадь выпуклого четырехугольника с перпендикулярными диагоналямиСкачать  Геометрия Точки M и N лежат на стороне AC треугольника ABC на расстояниях соответственно 8 и 30 отСкачать  Доказать, что точки лежат на одной окружностиСкачать  Геометрия Четырехугольник оказался вписанным Задача №26 ОГЭСкачать  №785. Точки М и N — середины диагоналей АС и BD четырехугольника ABCD.Скачать  🔴 В параллелограмме ABCD отмечена точка M ... | ЕГЭ БАЗА 2018 | ЗАДАНИЕ 15 | ШКОЛА ПИФАГОРАСкачать  Задание 26 Площадь четырехугольникаСкачать  Геометрия. Задача. Четырёхугольник. Окружность.Скачать  Задача с четырёхугольником из ТкачукаСкачать  |