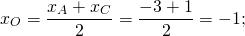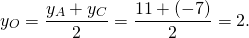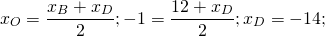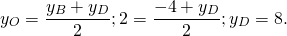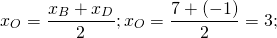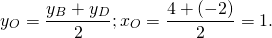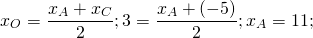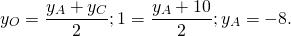Векторы даны три точки параллелограмма найти четвертую

Как найти координаты 4-й вершины параллелограмма, зная координаты трёх других его вершин?

В декартовых координатах эту задачу можно решить, используя свойство диагоналей параллелограмма.

Из трёх известных вершин две являются концами одной диагонали. Находим координаты середины этой диагонали. Точка пересечения диагоналей является серединой каждой из них. Для второй диагонали находим второй конец по известным одному концу и середине.

Дано: ABCD — параллелограмм,

1) Найдём координаты точки O — середины диагонали AC.

2) По свойству диагоналей параллелограмма, точка O также является серединой BD:

Дано: ABCD — параллелограмм,

1) Ищем координаты точки O — середины отрезка BD:

2) Точка O также является серединой AC:

Видео:1. Векторы и параллелограмм задачи №1Скачать

2 Comments

А как вы получили -14 в первом примере.

Можно применить основное свойство пропорции: 12+xD=2∙(-1), xD=-2-12=-14.

Видео:Найдите вершину A параллелограмма ABCD, если B(3; −4; 7), C(−5; 3; −2) и D(1; 2; −3)Скачать

Please wait.

Видео:№933. Найдите координаты вершины D параллелограмма ABCD, если А (0; 0), B (5; 0), С (12; -3.).Скачать

We are checking your browser. mathvox.ru

Видео:Вектор. Сложение и вычитание. 9 класс | МатематикаСкачать

Why do I have to complete a CAPTCHA?

Completing the CAPTCHA proves you are a human and gives you temporary access to the web property.

Видео:Найдите площадь треугольника АВС, если А(5;2;6), В(1;2;0), С(3;0;3)Скачать

What can I do to prevent this in the future?

If you are on a personal connection, like at home, you can run an anti-virus scan on your device to make sure it is not infected with malware.

If you are at an office or shared network, you can ask the network administrator to run a scan across the network looking for misconfigured or infected devices.

Another way to prevent getting this page in the future is to use Privacy Pass. You may need to download version 2.0 now from the Chrome Web Store.

Cloudflare Ray ID: 6d40003a0ca49045 • Your IP : 85.95.179.65 • Performance & security by Cloudflare

Видео:Уравнения стороны треугольника и медианыСкачать

Даны 3 вектора найти четвертый

Видео:Нахождение координат вектора. Практическая часть. 9 класс.Скачать

Задача 29832 даны три вектора а=(3,-2,4), в=(5,1,6).

Условие

даны три вектора а=(3,-2,4), в=(5,1,6), с=(-3,0,2) найти вектор х удовлетворяющий трем уравнениям: (а ^ x)=4 (b ^ x)=35 (c ^ x)=0

Все решения

Пусть вектор х имеет координаты (x_(1);x_(2);x_(3)).

Скалярное произведение векторов, заданных своими координатами равно сумме произведений одноименных координат.

Видео:Математика без Ху!ни. Смешанное произведение векторовСкачать

Найти четвертую вершину параллелограмма

Как найти координаты 4-й вершины параллелограмма, зная координаты трёх других его вершин?

В декартовых координатах эту задачу можно решить, используя свойство диагоналей параллелограмма.

Из трёх известных вершин две являются концами одной диагонали. Находим координаты середины этой диагонали. Точка пересечения диагоналей является серединой каждой из них. Для второй диагонали находим второй конец по известным одному концу и середине.

Дано: ABCD — параллелограмм,

1) Найдём координаты точки O — середины диагонали AC.

2) По свойству диагоналей параллелограмма, точка O также является серединой BD:

Дано: ABCD — параллелограмм,

1) Ищем координаты точки O — середины отрезка BD:

2) Точка O также является серединой AC:

Видео:Вычитание векторов. 9 класс.Скачать

2 Comments

А как вы получили -14 в первом примере.

Можно применить основное свойство пропорции: 12+xD=2∙(-1), xD=-2-12=-14.

Видео:Нахождение длины вектора через координаты. Практическая часть. 9 класс.Скачать

3.1.7. Примеры решения задач по теме «Линейные операции над векторами. Скалярное произведение»

Даны векторы А = (-2; 3; 5) и B = (4; -1; 7). Найти координаты вектора

При умножении вектора на число все его координаты

Умножаются на это число, при сложении векторов складываются их соответствующие координаты.

Координаты коллинеарных векторов пропорциональны.

Если A || B, то . Отсюда:

Ответ: .

Найти направляющие косинусы вектора А = .

Направляющие косинусы являются координатами орта (единичного вектора) данного направления.

Найдем модуль вектора А:

Разделив все координаты вектора А на его модуль, получим координаты орта:

Ответ:

Тогда AA + BB + GC = , причем координаты этого вектора должны равняться соответствующим координатам вектора D. Приравнивая эти координаты, получаем систему уравнений для определения A, B, G:

Для векторов A = , B = , C = , D = найти такие числа A, B, G, чтобы векторы AA, BB, GC и D образовали замкнутую ломаную линию, если начало каждого последующего вектора совместить с концом предыдущего.

C = линейно зависимой или линейно независимой.

Система векторов называется линейно независимой, если равенство

Вычислим главный определитель Δ системы уравнений

По правилу Крамера система имеет единственное решение, но для однородной системы всегда существует нулевое решение (A = B = G = 0).

Поскольку других решений нет, данная система векторов линейно независима.

Ответ: Система векторов линейно независима.

Найти координаты какого-либо вектора, направленного по биссектрисе угла между векторами А = (-4; 3; 0) и B = (12; -15; 16).

Диагональ параллелограмма является биссектрисой угла между сторонами только в том случае, если этот параллелограмм – ромб. Следовательно, искомым вектором можно считать сумму двух векторов равной длины, коллинеарных соответственно векторам А и B.

Вектор A + B направлен по диагонали параллелограмма, построенного на векторах А и B как на смежных сторонах и выходящей из общего начала векторов А и B.

Диагональ параллелограмма является биссектрисой угла между сторонами только в том случае, если этот параллелограмм – ромб. Следовательно, искомым вектором можно считать сумму двух векторов равной длины, коллинеарных соответственно векторам А и B.

Следовательно, |5A| = |B|. Значит, параллелограмм со сторонами, совпадающими с векторами 5A и B, является ромбом, поэтому вектор 5A + B будет иметь заданное направление.

При каких значениях X, Y, Z точки А(Х; -1; 3), В(5; -4; Z), C(-2; Y; 9), D(-5; 1; 7) являются вершинами параллелограмма?

Для выполнения условия задачи требуется коллинеарность векторов и и и .

Для выполнения условия задачи требуется коллинеарность векторов и и и .

Найдем координаты этих векторов:

Из последней пропорции получаем, что Z = 1 – 2Y. Тогда

Но при этих значениях неизвестных

Условие задачи выполнено.

Используйте определение скалярного произведения:

Используем свойства скалярного произведения:

По определению скалярного произведения

Сложим левые и правые части полученных равенств:

Даны векторы А = и B = . Найти скалярное произведение

Найдите координаты векторов 3А – B и A + 2B или используйте свойства скалярного произведения.

Используем свойства скалярного произведения:

Используйте формулу, выражающую косинус угла между векторами через их скалярное произведение.

Ответ: .

Координаты вектора B пропорциональны координатам А. Если K – коэффициент пропорциональности, то B = .

Координаты вектора B пропорциональны координатам А. Если K – коэффициент пропорциональности, то B = .

Известно, что |A| = 2, |B| = 7. Найти значения K, при которых векторы

Если векторы перпендикулярны, то их скалярное произведение равно нулю.

Если векторы перпендикулярны, то их скалярное произведение равно нулю.

Ответ: K = .

Найти проекцию вектора А = на ось, образующую с координатными осями Ох и Оу углы 60о и 45о, а с осью Oz – тупой угол γ.

Используйте свойство направляющих косинусов:

Найдем cosγ: cos260o + cos245o + cos2γ = 1,

Тогда проекция А на заданную ось равна:

🎬 Видео

Прямоугольная система координат в пространстве. 11 класс.Скачать

Площадь параллелограмма, построенного на данных векторахСкачать

4. Уравнение плоскости проходящей через три точки / в отрезках / доказательство и примерыСкачать

№783. Точка М лежит на стороне ВС параллелограмма ABCD, причем ВМ:МС=3:1. ВыразитеСкачать

Угол между векторами. 9 класс.Скачать

Координаты вектора. 9 класс.Скачать

№934. Найдите координаты вектора АВ, зная координаты его начала и конца: а) А (2; 7), B (-2; 7);Скачать

Даны вершины пирамиды A, B, C, D. Найдите объём пирамиды и высоту, опущенную на грань ACDСкачать

18+ Математика без Ху!ни. Скалярное произведение векторов. Угол между векторами.Скачать

Угол между векторами | МатематикаСкачать