Алгоритм построения окружности в аксонометрии (3 видео)

Построение аксонометрических проекций окружности

Построение аксонометрических проекций окружности вызывает трудности, в связи с тем, что окружность принимает вид эллипса в аксонометрии. Возникает вопрос: как рисовать эллипс? Чтобы построить окружность в аксонометрии используют следующие способы: — построение по вспомогательной квадратной сетке; — построение при помощи циркуля;

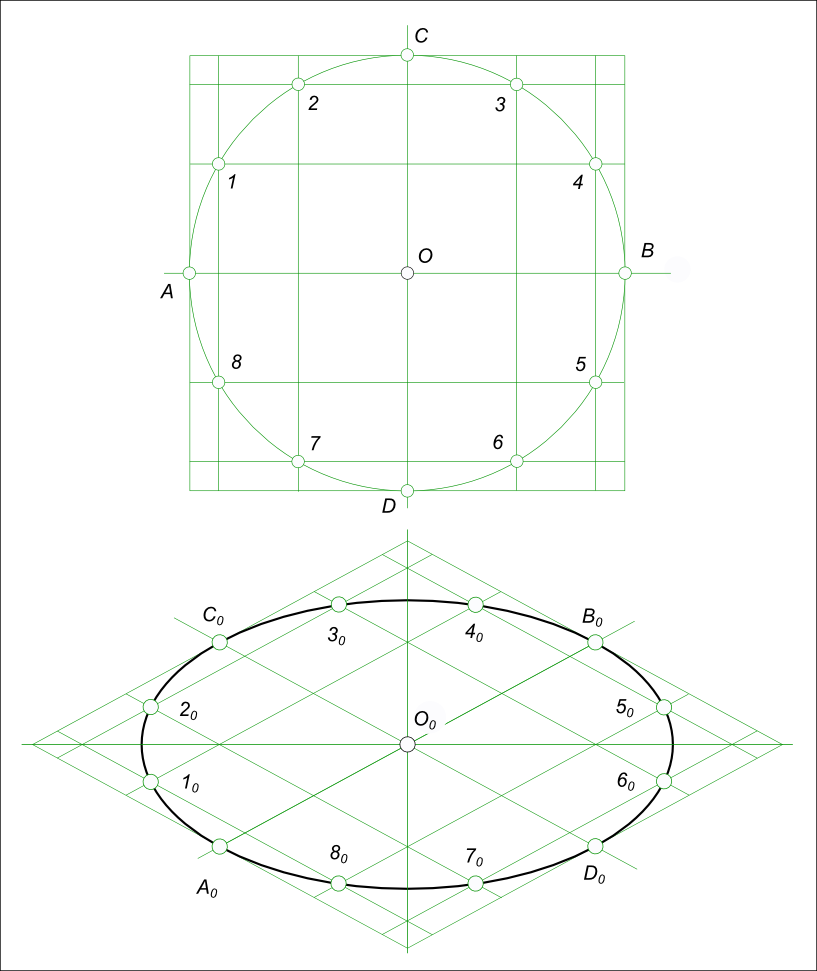
По первому способу квадрат описывает окружность и делится на 4×4=16. Отмечаем точки пересечения линий сетки с линией окружности. Затем строим аксонометрическую проекцию сетки и на ней отмечаем точки A₀, 1₀, 2₀, . 8₀. По этим точкам строим окружность, при помощи лекала. Данным способом окружность строится также в перспективе.

Окружность для данного вида аксонометрической проекции — прямоугольной изометрии получилась получилась несколько больше своего действительного размера, в следствии применения приведенных коэффициентов искажения.

По второму способу окружность строится при помощи циркуля Построение аксонометрических проекций окружности в косоугольной фронтальной диметрии

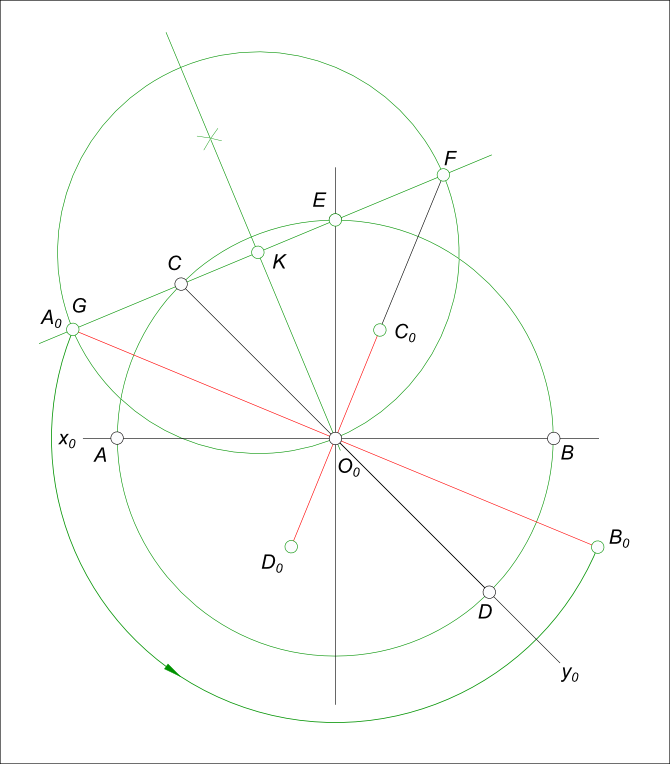
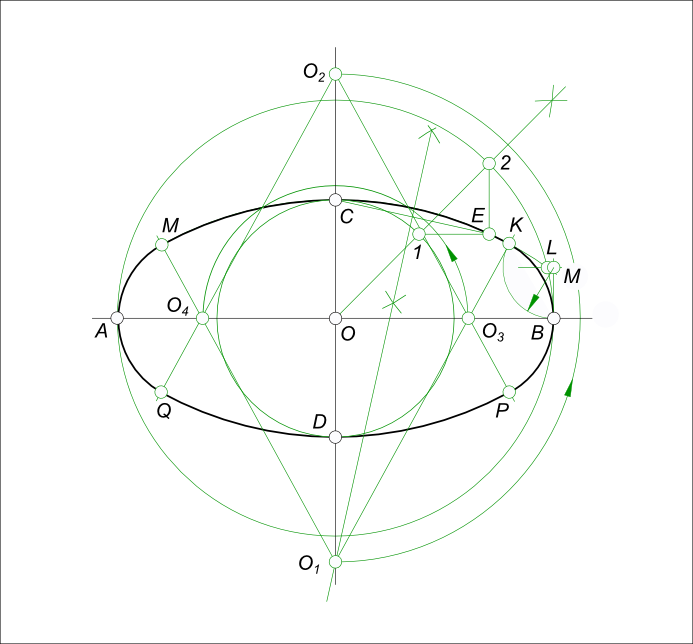
Пусть окружность расположена параллельно горизонтальной плоскости проекции: — сначала определяем направление большой и малой оси эллипса, используя для этого построение показанное на рисунке Сопрягаемые диаметры AB и CD построены на аксонометрических осях x₀ и y₀, их центры совпадают с началом координат. Концы одного из диаметров (AB) соединим дугой окружности из центра O₀. Восстановив перпендикуляр к диаметру в точке O₀ отметим на их пересечении точку E. Соединяем точки C, E прямой линией. Находим середину отрезка CE — точку K. Из точки K описываем окружность радиусом KO₀ и отмечаем точки F и G, в которых она пересекается с прямой CE. Длина половины большой оси равна отрезкам GE, CF, длина половины малой оси равна отрезкам CG, EF; — затем, после построения осей эллипса:

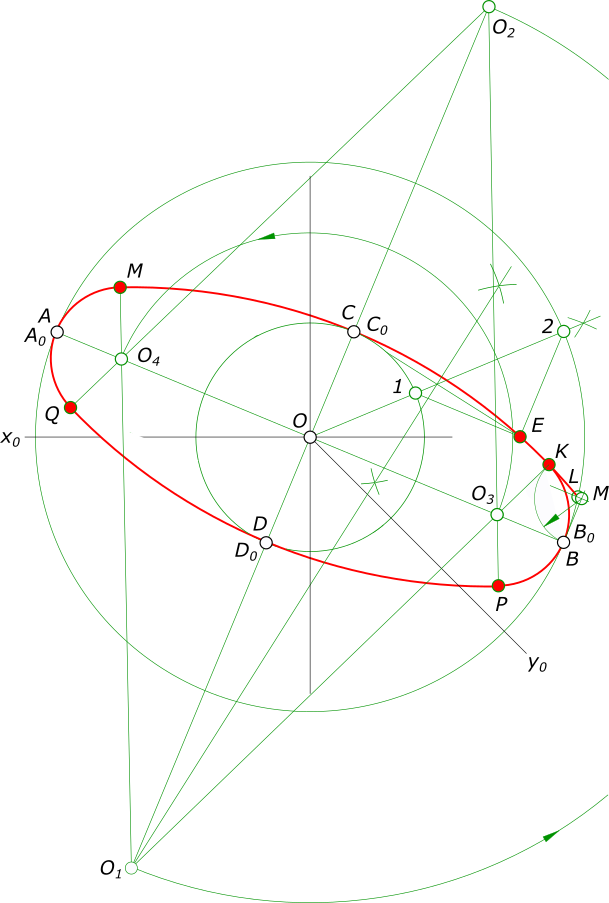
— проводим прямую O — 2 делящую угол между осями пополам при этом находим точки 1 и 2 пересечения данной прямой с окружностями малой и большой оси; — из точки 1 проводим прямую параллельную большой оси, а из точки 2 проводим прямую параллельную малой оси и на их пересечении находим точку эллипса E; — соединяем точки E, C прямой линией. Через середину отрезка CE восстанавливаем к нему перпендикуляр до пересечения с малой осью в точке O₁, которая определяет центр дуги CE; — строим точку O₂ симметричную O₁, относительно центра эллипса — O; — на пересечении дуг CE и 2B отмечаем точку L, проводим через данную точку прямую параллельную большой оси до пересечения ее в точке M с прямой BM, перпендикулярной большой оси — OB; — из центра M проводим дугу радиусом MB до пересечения ее с дугой CE в точке K, являющейся точкой сопряжения дуг овала; — соединив прямой линией точки K и O₁ на пересечении ее с большой осью находим точку O₃, являющуюся центром дуги BK; — точку P находим на пересечении прямой O₂O₃ с дугой радиусом O₃B. P — точка сопряжения дуг BK и BP; — точке O₃ симметрична относительно центра эллипса точка O₄; — аналогично, построив точки сопряжения для левой половины , проводим дуги овала, предварительно удалив ненужные построения.

Построение аксонометрических проекций окружности в прямоугольной изометрии

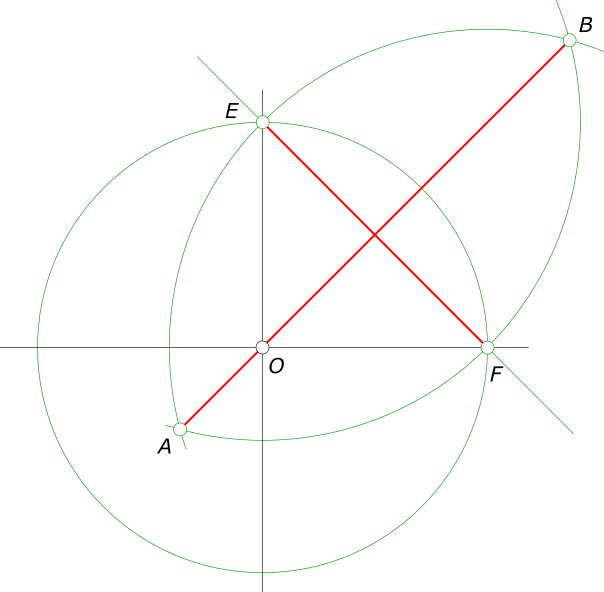
Графически определяем размеры осей эллипса: — проводим две взаимно перпендикулярные линии; — приняв точку их пересечения за центр O, описываем из него окружность заданного диаметра и отмечаем точки E и F; — из точек E и F описываем дуги радиусом R = EF = FE и находим точки их пересечения A и B; — соединив точки A и B, получим большую ось эллипса, равную 1,22d; — соединив точки E и F, получим малую ось эллипса, равную 0,7d

Пусть, строится окружность, расположенная параллельно горизонтальной плоскости проекции

где большая ось AB перпендикулярна свободной оси (z) и малая ось CD. — затем, после построения осей эллипса: — проводим прямую O — 2 делящую угол между осями пополам при этом находим точки 1 и 2 пересечения данной прямой с окружностями малой и большой оси; — из точки 1 проводим прямую параллельную большой оси, а из точки 2 проводим прямую параллельную малой оси и на их пересечении находим точку эллипса E; — соединяем точки E, C прямой линией. Через середину отрезка CE восстанавливаем к нему перпендикуляр до пересечения с малой осью в точке O₁, которая определяет центр дуги CE; — строим точку O₂ симметричную O₁, относительно центра эллипса — O; — на пересечении дуг CE и 2B отмечаем точку L, проводим через данную точку прямую параллельную большой оси до пересечения ее в точке M с прямой BM, перпендикулярной большой оси — OB; — из центра M проводим дугу радиусом MB до пересечения ее с дугой CE в точке K, являющейся точкой сопряжения дуг овала; — соединив прямой линией точки K и O₁ на пересечении ее с большой осью находим точку O₃, являющуюся центром дуги BK; — точку P находим на пересечении прямой O₂O₃ с дугой радиусом O₃B. P — точка сопряжения дуг QP и BP; — точке O₃ симметрична относительно центра эллипса точка O₄; — аналогично, построив точки сопряжения для левой половины , проводим дуги овала, предварительно удалив ненужные построения.

Более просто выглядит построение окружности, расположенной параллельно горизонтальной плоскости проекции

Видео:Аксонометрические Проекции Окружности #черчение #окружность #проекции #изометрияСкачать

Построение окружности в аксонометрии

Окружности, лежащие в плоскостях, параллельных плоскостям проекций, проецируются на аксонометрическую плоскость проекций в эллипсы.

Малая ось эллипса всегда располагается вдоль отсутствующей оси в плоскости проекций. Большая ось эллипса перпендикулярна его малой оси. Так, в плоскости ХОY малая ось расположена вдоль оси Z, в плоскости ХОZ – вдоль оси Y, в плоскости YОZ – вдоль оси Х.

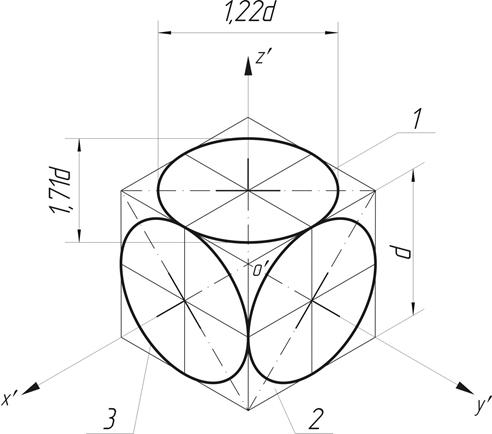
В прямоугольной изометрии большая ось эллипсов 1, 2, 3 равна 1,22 диаметра окружности, а малая – 0,71 диаметра окружности (рис. 2.29).

В прямоугольной диметрии большая ось эллипсов 1, 2, 3 равна 1,06 диаметра окружности, а малая ось эллипса 1 – 0,95d, эллипсов 2, 3 – 0,35d. Величину большой и малой оси подсчитывают или определяют графическим путем (рис. 2.30).

В косоугольной фронтальной диметрии окружности, лежащие в плоскостях, параллельных фронтальной плоскости проекций, проецируются на аксонометрическую плоскость в виде окружности; окружности, лежащие в плоскостях, параллельных горизонтальной и профильной плоскостям проекций, – в виде эллипсов (рис. 2.31). При этом большая ось эллипсов равна 1,07d, а малая ось – 0,33d. Большая ось горизонтального эллипса с осью Х составит угол 7°14′, и тот же угол будет между осью Z и большой осью профильного эллипса.

Фронтальную диметрию целесообразно применять в тех случаях, когда необходимо сохранить неискаженными фигуры, расположенные во фронтальных плоскостях.

На практике принято заменять эллипсы овалами, что значительно облегчает построение.

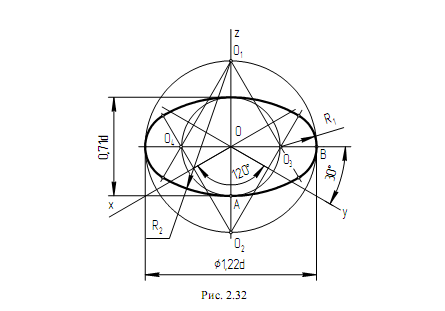
Пример выполнения овала, расположенного в горизонтальной плоскости проекций, дан на рис. 2.32.

Построение овала начинают с проведения осей симметрии и аксонометрических осей. Большая ось равна 1,22d, малая ось – 0,71d, где d – диаметр изображаемой окружности. Через точку О – начало аксонометрических осей – проводят окружности, диаметры которых соответственно равны большой и малой осям эллипса. На вертикальном диаметре большой окружности отмечают центры О1 и О2, а на горизонтальном диаметре малой окружности – О3 и О4. Эти точки являются центрами сопряжения дуг овала. Проводят прямые О2О3, О2О4, О1О3, на которых расположены точки со-

пряжения дуг овала. Две дуги радиуса R1 = О3В описывают из центров О3 и О4, а две другие радиуса R2 = О1А – из центров О1 и О2.

Для построения овала, расположенного в горизонтальной плоскости проекций, можно использовать и другой способ (рис. 2.33). В прямоугольной изометрии малую ось овала будем располагать вдоль оси Z, большую ось проведем перпендикулярно к малой оси. Из точки О пересечения этих осей циркулем сделаем засечки на осях Х и Y радиусом, равным радиусу заданной окружности.

Полученные точки 1, 2, 3, 4 являются точками сопряжения дуг овала.

Из точки 1, лежащей на оси Х, проведем перпендикуляр к оси Y. На пересечении перпендикуляра с большой и малой осями получим две точки О1 и О2, которые являются центрами сопряжения дуг овала. Из точек О1 и О2 радиусами R1 = О1 – 1 и R2 = О2 – 1 опишем дуги окружностей. Аналогично построим две другие дуги. Построение будем проводить из точки 3. Перпендикуляр, проведенный из точки 3 к оси Y, даст нам еще два центра: О3 и О4, из которых радиусами R1= О3 – 3 и R2 = О4 – 3 опишем дуги окружностей.

Во фронтальной и профильной плоскостях построение овалов аналогично.

Рассмотрим построение прямоугольной диметрии овала, заменяющего эллипс, в который проецируется окружность, расположенная в плоскости П1 (рис. 2.34). Через точку О проводим оси диметрии ОХ, ОY, ОZ и направление большой оси овала перпендикулярно оси ОZ. Малая ось совпадет с направлением оси ОZ. Вдоль большой оси овала откладывают длину, равную 1,06d; вдоль малой оси – величину 0,35d. Для определения положения центра О1 сопряжения большой дуги овала откладывают вдоль малой оси от точки О величину 1,06d. От точки В откладывают величину ВО2, равную 0,09d, и определяют положение центра сопряжения О2 малой дуги овала.

Проводят линии центров О1О2 и т.д. Из центра О2 радиусом R = О2В проводят дугу овала до пересечения с линией центров в точке сопряжения. Из центра О1 радиусом R = О1А проводят большую дугу овала. Аналогично проводят дуги из двух не указанных на чертеже центров.

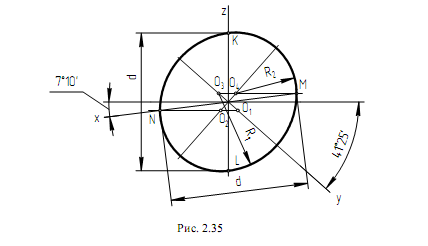
При построении прямоугольной диметрии овала, расположенного в плоскости П2 (рис. 2.35), через точку О проводят оси диметрии ОХ, ОY, ОZ. Через точку О проводят направление большой оси овала перпендикулярно оси Оу. Малая ось совпадает с направлением оси ОY. На осях ОY и ОZ откладывают величину d изображаемой окружности и получают точки М, N, K, L, являющиеся точками сопряжения дуг овала. Через точки М и N проводят горизонтальные прямые, которые в пересечении с осью Оу и перпендикуляром к ней дают точки О1, О2, О3, О4 – центры дуг овала. Из центров О1 и О3 описывают дуги радиусом R1 = О3L, а из центров О4 и О2 – дуги радиусом R2 = О4М.

В профильной плоскости построение овала аналогично построению овала в горизонтальной плоскости с учетом расположения большой и малой осей овала.

Видео:ПОСТРОЕНИЕ ОВАЛА │ КАК НАЧЕРТИТЬ ОВАЛ ПРИ ПОСТРОЕНИИ АКСОНОМЕТРИИ │ Урок #61Скачать

Построение окружностей в стандартных аксонометрических проекциях.

Изометрическими проекциями окружностей, расположенных в плоскостях проекций или в плоскостях, параллельных им, являются эллипсы с одинаковыми соотношениями осей (рис.47).

Рис.47. Изометрические проекции окружности

Большие оси эллипсов равны 1,22d, а малые — 0,71 d , где d — диаметр изображаемой окружности.

Для упрощения построений допускается заменять эллипсы овалами, очерченными дугами окружностей.

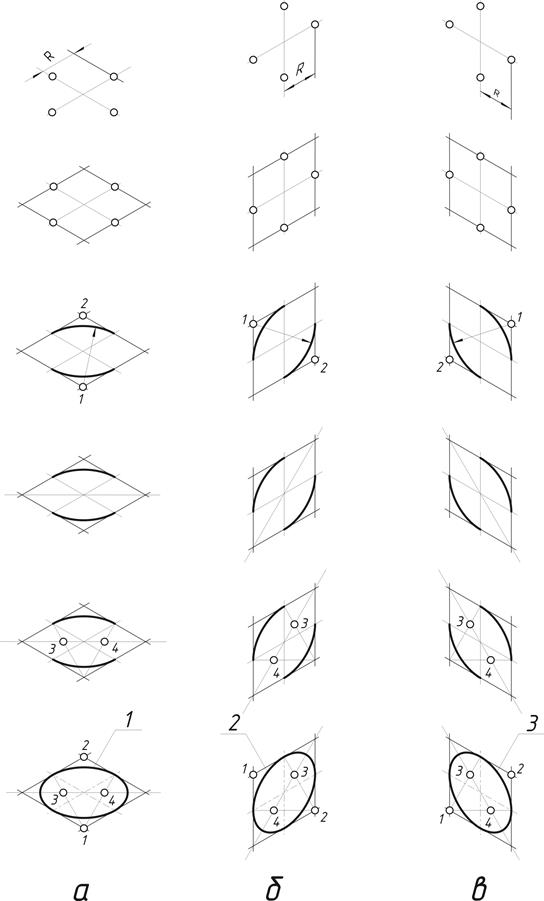
На рис.48 приведена последовательность построения четырехцентровых овалов, приближенно заменяющих проекции окружности, расположенной в плоскости проекций или ей параллельной. Данный способ является наиболее простым в построении.

Рис.48. Построение овалов: а — в координатной плоскости х 1 0 1 у 1 , б — в координатной плоскости у 1 0 1 z 1 ; в — в координатной плоскости у 1 0 1 z 1

Разрезы в аксонометрии, как правило, выполняют плоскостями,
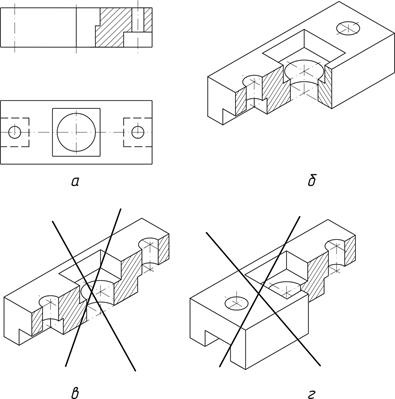
отличными о тех, которыми производят разрезы на комплексном чертеже (рис.49,а, 49,б). Плоскости разрезов аксонометрии должны либо совпадать с координатными плоскостями, либо располагаться параллельно им.

Рис.49. Разрезы в аксонометрии

Чаще всего плоскости разрезов в аксонометрии совпадают с главными плоскостями симметрии предмета (рис 49,б).

Нельзя применять в аксонометрии только одну секущую плоскость, изображая половину предмета, так как при этом исчезает один из трех габаритных размеров и изображений теряет наглядность (рис.498,в))

Разрезы в аксонометрии должны всегда просматриваться и быть обращенными к наблюдателю (рис.49,г).

Последовательность построения аксонометрической проекции предмета

Дата добавления: 2016-09-06 ; просмотров: 2943 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ