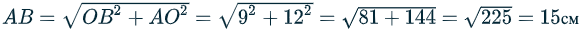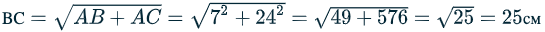Наклонная призма основание треугольника

Содержание:

Призмой зовётся объёмный многогранник, состоящий из двух одинаковых основ – многоугольников, расположенных в перпендикулярных плоскостях. Её боковые грани – прямоугольники или параллелограммы, имеют с ними общие грани. Наклонная призма – геометрическое тело с рёбрами, расположенными к основаниям под углом, отличным от прямого. Её верхняя и нижняя плоскости остаются параллельными.

Видео:Объем наклонной призмы. Урок 15. Геометрия 11 классСкачать

Разновидности

Полная поверхность – сумма боковых поверхностей, нижней и верхней. Боковая – представлена параллелограммами. Расстояние между плоскостями оснований зовётся высотой геометрического тела.

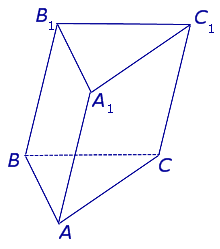
Наклонная трехгранная или треугольная призма представлена пятигранником с равными основаниями в виде треугольников, которые смещены друг относительно друга. Боковые ребра наклонены к основанию.

Объём вычисляется по классической формуле:

Полная площадь: S = S_бок + 2S_осн или P_оснh + 2S_осн.

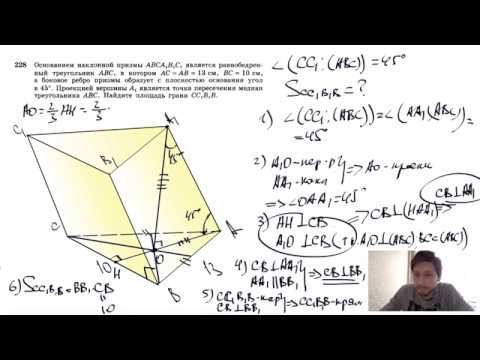
Видео:№228. Основанием наклонной призмы АВСА1В1С1 является равнобедренный треугольник ABCСкачать

Сечения

Сечением тела называется фигура, представленная всеми его точками, расположенными на плоскости α. Перпендикулярное сечение наклонной призмы пересекает её боковые рёбра под углом 90°.

• Перпендикулярные сечения геометрического тела равны один другому.
• Сечение будет перпендикулярным боковым ребрам.

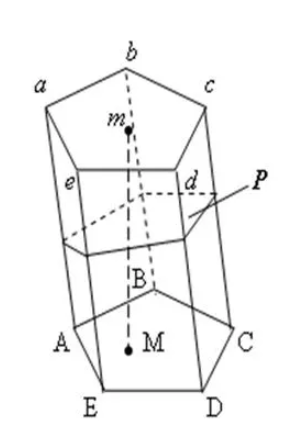
Если под углом 90° к боковым граням проходит плоскость сечения, геометрическая фигура называется усечённой. Периметр перпендикулярного сечения такой призмы равен:

• P – периметр фигуры сечения;
• l – боковое ребро, например, dD.

Видео:2.2. Наклонная призма.Скачать

Задача

Перпендикулярным сечением наклонной четырехугольной призмы является ромб с диагоналями BD = 24 см, AC = 18 см. Боковая поверхность – 780 см2. Вычислить боковое ребро геометрической фигуры.

Начнём с рассмотрения перпендикулярного сечения. Стороной призмы является высота пересекающей плоскости. Сторона ромба вычисляется благодаря прямоугольному треугольнику AOB, где катеты равны половине диагонали (особенность рассматриваемого многоугольника).

Половины диагоналей OB и AO равны 9 и 12 см.

Воспользуемся теоремой Пифагора:

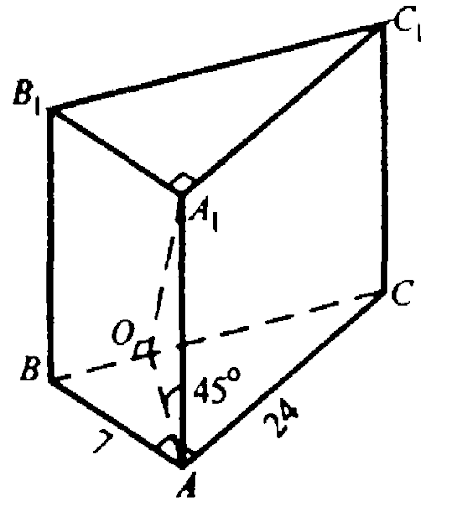
Дана наклонная призма, в основании которой лежит прямоугольный треугольник. Катеты равны 7 и 24 см. Вершина A₁ находится на одинаковом удалении от вершин треугольника. Вычислить высоту призмы, где ребро AA₁ находится под углом 45° к основанию.

Проекция точки A1 на сторону BC △АВС представлена точкой O – это центр окружности, описанной вокруг нижнего основания △АВС. Отсюда следует: O делит гипотенузу ВС на равные отрезки BO = OC. Причём BC ⊥ А₁О – высота геометрического тела.

ΔА₁ОА является равнобедренным прямоугольным, а отрезки А₁О и АО равны.

Воспользуемся теоремой Пифагора.

Расстояния от вершин до точки O равны 25 : 2 = 12,5 см.

Видео:Наклонная призмаСкачать

Треугольная призма все формулы и примеры задач

Треугольная призма — это трехмерное тело, образованное соединением прямоугольников и треугольников. В этом уроке вы узнаете, как найти размер внутри (объем) и снаружи (площадь поверхности) треугольной призмы.

Видео:11 класс, 34 урок, Объем наклонной призмыСкачать

Определение

Треугольная призма — это пятигранник, образованный двумя параллельными плоскостями, в которых расположены два треугольника, образующих две грани призмы, и оставшиеся три грани — параллелограммы, образованные со-сторонами треугольников.

Видео:№238. В наклонной треугольной призме две боковые грани взаимно перпендикулярны, а их общее реброСкачать

Элементы треугольной призмы

Треугольники ABC и A₁B₁C₁ являются основаниями призмы .

Четырехугольники A₁B₁BA, B₁BCC₁ и A₁C₁CA являются боковыми гранями призмы .

Стороны граней являются ребрами призмы (A₁B₁, A₁C₁, C₁B₁, AA₁, CC₁, BB₁, AB, BC, AC), всего у треугольной призмы 9 граней.

Высотой призмы называется отрезок перпендикуляра, который соединяет две грани призмы (на рисунке это h).

Диагональю призмы называется отрезок, который имеет концы в двух вершинах призмы, не принадлежащих одной грани. У треугольной призмы такой диагонали провести нельзя.

Площадь основания — это площадь треугольной грани призмы.

Площадь боковой поверхности призмы — это сумма площадей четырехугольных граней призмы.

Видео:Задача 1. 4 Нахождение высоты наклонной призмыСкачать

Виды треугольных призм

Треугольная призма бывает двух видов: прямая и наклонная.

У прямой призмы боковые грани прямоугольники, а у наклонной боковые грани — параллелограммы (см. рис.)

Прямая треугольная призма

Призма, боковые ребра которой перпендикулярны плоскостям оснований, называется прямой.

Наклонная треугольная призма

Призма, боковые ребра которой являются наклонными к плоскостям оснований, называется наклонной.

Видео:10 класс, 30 урок, ПризмаСкачать

Основные формулы для расчета треугольной призмы

Объем треугольной призмы

Чтобы найти объем треугольной призмы, надо площадь ее основания умножить на высоту призмы.

Объем призмы = площадь основания х высота

Площадь боковой поверхности призмы

Чтобы найти площадь боковой поверхности треугольной призмы, надо периметр ее основания умножить на высоту.

Площадь боковой поверхности треугольной призмы = периметр основания х высота

Площадь полной поверхности призмы

Чтобы найти площадь полной поверхности призмы, надо сложить ее площади оснований и площадь боковой поверхности.

так как S_бок=P_осн . h, то получим:

Правильная призма — прямая призма, основанием которой является правильный многоугольник.

Свойства призмы :

Верхнее и нижнее основания призмы – это равные многоугольники.
Боковые грани призмы имеют вид параллелограмма.
Боковые ребра призмы параллельные и равны.

Совет: при расчете треугольной призмы вы должны обратить внимание на используемые единицы. Например, если площадь основания указана в см 2 , то высота должна быть выражена в сантиметрах, а объем — в см 3 . Если площадь основания в мм 2 , то высота должна быть выражена в мм, а объем в мм 3 и т. д.

Видео:Как строить сеченияСкачать

Пример призмы

В этом примере:
— ABC и DEF составляют треугольные основания призмы
— ABED, BCFE и ACFD являются прямоугольными боковыми гранями
— Боковые края DA, EB и FC соответствуют высоте призмы.
— Точки A, B, C, D, E, F являются вершинами призмы.

Видео:Наклонная призма | Стереометрия #39 | ИнфоурокСкачать

Задачи на расчет треугольной призмы

Задача 1. Основанием прямой треугольной призмы служит прямоугольный треугольник с катетами 6 и 8, боковое ребро равно 5. Найдите объем призмы.
Решение: Объем прямой призмы равен V = Sh, где S — площадь основания, а h — боковое ребро. Площадь основания в данном случае это площадь прямоугольного треугольника (его площадь равна половине площади прямоугольника со сторонами 6 и 8). Таким образом, объём равен:

V = 1/2 · 6 · 8 · 5 = 120.

Задача 2.

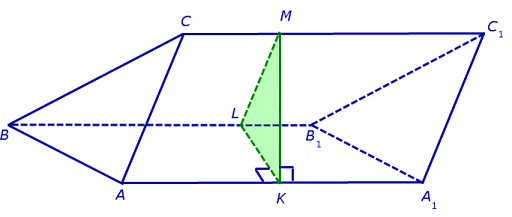
Через среднюю линию основания треугольной призмы проведена плоскость, параллельная боковому ребру. Объем отсеченной треугольной призмы равен 5. Найдите объем исходной призмы.

Решение:

Объём призмы равен произведению площади основания на высоту: V = S_осн ·h.

Треугольник, лежащий в основании исходной призмы подобен треугольнику, лежащему в основании отсечённой призмы. Коэффициент подобия равен 2, так как сечение проведено через среднюю линию (линейные размеры большего треугольника в два раза больше линейных размеров меньшего). Известно, что площади подобных фигур соотносятся как квадрат коэффициента подобия, то есть S₂ = S₁k 2 = S₁2 2 = 4S₁.

Площадь основания всей призмы больше площади основания отсечённой призмы в 4 раза. Высоты обеих призм одинаковы, поэтому объем всей призмы в 4 раза больше объема отсечённой призмы.

Таким образом, искомый объём равен 20.

Формулы по математике для ЕГЭ и ОГЭ

Шар и сфера, объем шара, площадь сферы, формулы

Видео:НАКЛОННАЯ ПРИЗМА // СТЕРЕОМЕТРИЯСкачать

Наклонная призма и ее объем. Пример решения задачи

Умение определять объем пространственных фигур является важным для решения геометрических и практических задач. Одной из таких фигур является призма. Рассмотрим в статье, что она собой представляет, и покажем, как вычислять объем наклонной призмы.

Видео:№230. Основание прямой призмы — треугольник со сторонами 5 см и 3 см и углом, равным 120Скачать

Что понимают под призмой в геометрии?

Речь идет о правильном полиэдре (многограннике), который образован двумя одинаковыми основаниями, находящимися в параллельных плоскостях, и несколькими параллелограммами, соединяющими отмеченные основания.

Основаниями призмы могут быть произвольные многоугольники, например, треугольник, четырехугольник, семиугольник и так далее. Причем число углов (сторон) многоугольника определяет название фигуры.

Любая призма, имеющая в основании n-угольник (n — число сторон), состоит из n+2 граней, 2 × n вершин и 3 × n ребер. Из приведенных чисел видно, что количества элементов призмы соответствуют теореме Эйлера:

Ниже рисунок показывает, как выглядят треугольные и четырехугольные призмы, сделанные из стекла.

Видео:Объём наклонной призмы, пирамиды и конуса. 11 классСкачать

Виды фигуры. Наклонная призма

Выше уже было сказано, что название призмы определяется числом сторон многоугольника в основании. Однако существуют и другие особенности в ее строении, определяющие свойства фигуры. Так, если все параллелограммы, образующие боковую поверхность призмы, представлены прямоугольниками или квадратами, то такая фигура называется прямой. Для прямой призмы расстояние между основаниями равно длине бокового ребра любого прямоугольника.

Если же некоторые или все боковые стороны являются параллелограммами, то речь идет о наклонной призме. Высота ее уже будет меньше, чем длина бокового ребра.

Еще один критерий, по которому проводят классификацию рассматриваемых фигур — это длины сторон и углы многоугольника в основании. Если они равны друг другу, то многоугольник будет правильным. Прямая фигура с правильным многоугольником в основаниях называется правильной. С ней удобно работать при определении площади поверхности и объема. Наклонная призма в этом плане представляет некоторые трудности.

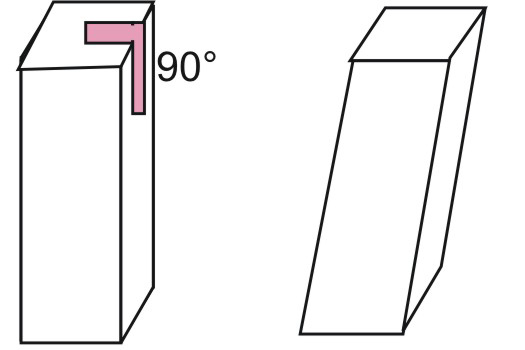
На приведенном рисунке показаны две призмы, имеющие четырехугольное основание. Угол 90° показывает принципиальную разницу между прямой и наклонной призмой.

Видео:Определение натуральной величины треугольника АВС методом замены плоскостей проекцииСкачать

Формула для определения объема фигуры

Часть пространства, ограниченная гранями призмы, называется ее объемом. Для рассматриваемых фигур любого типа эту величину можно определить по следующей формуле:

Здесь символом h обозначена высота призмы, которая является мерой дистанции между двумя основаниями. Символ S_o — одного основания площадь.

Площадь основания найти несложно. Учитывая тот факт, является правильным многоугольник или нет, а также зная количество его сторон, следует применить соответствующую формулу и получить S_o. Например, для правильного n-угольника с длиной стороны a площадь будет равна:

Теперь перейдем к высоте h. Для прямой призмы определение высоты не представляет никаких трудностей, однако для призмы наклонной — это непростая задача. Решать ее можно различными геометрическими методами, отталкиваясь от конкретных начальных условий. Тем не менее существует универсальный способ определения высоты фигуры. Опишем его кратко.

Идея заключается в нахождении расстояния от точки в пространстве до плоскости. Предположим, что плоскость задана уравнением:

Тогда от точки с координатами (x₁; y₁; z₁) плоскость будет находиться на расстоянии:

Если координатные оси расположить так, что точка (0; 0; 0) будет лежать в плоскости нижнего основания призмы, тогда уравнение для плоскости основания можно записать так:

Это означает, что формула для высоты запишется так:

Достаточно найти координату z любой точки верхнего основания, чтобы определить высоту фигуры.

Видео:№234. Основанием прямой призмы является прямоугольный треугольник. Через середину гипотенузыСкачать

Пример решения задачи

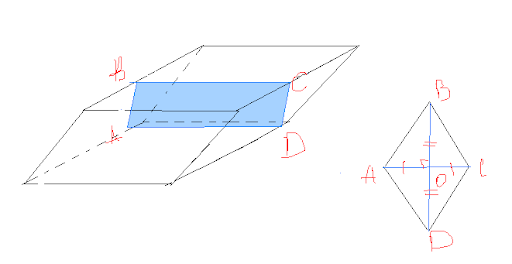
На рисунке ниже дана четырехугольная призма. Основанием наклонной призмы является квадрат со стороной 10 см. Необходимо вычислить ее объем, если известно, что длина бокового ребра равна 15 см, а острый угол фронтального параллелограмма равен 70°.

Поскольку высота h фигуры также является высотой параллелограмма, то используем формулы для определения его площади, чтобы найти h. Обозначим стороны параллелограмма так:

Тогда можно записать для него следующие формулы для определения площади S_p:

Здесь α — острый угол параллелограмма. Поскольку основанием является квадрат, то формула объема наклонной призмы примет вид:

Подставляем из условия данные в формулу и получаем ответ: V ≈ 1410 см 3 .

💥 Видео

Неравномерная темперация и биения центра объектовСкачать

СЕЧЕНИЯ. СТРАШНЫЙ УРОК | Математика | TutorOnlineСкачать

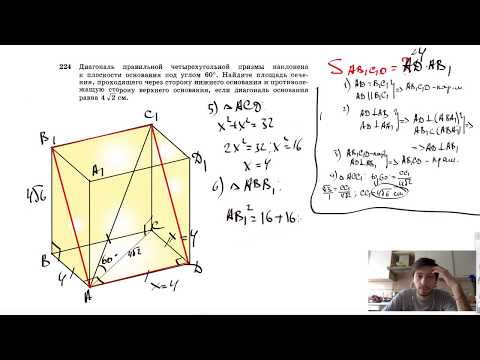
№224. Диагональ правильной четырехугольной призмы наклонена к плоскости основания под углом 60°Скачать

Геометрия 10 класс Тест 14 Наклонная призма Вариант 1 Задание С1Скачать

Площадь боковой поверхности наклонной призмы в ЕГЭСкачать