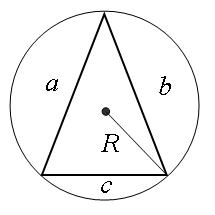
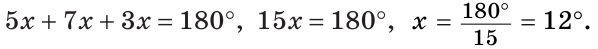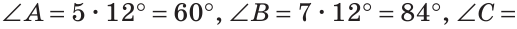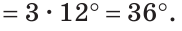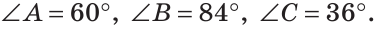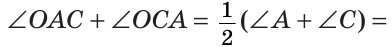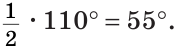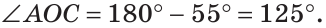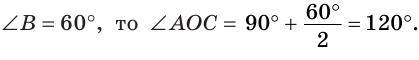С помощю этого онлайн калькулятора можно решить треугольники, т.е. найти неизвестные элементы (стороны, углы) треугольника. Теоретическую часть и численные примеры смотрите ниже.
Решение треугольников − это нахождение всех его элементов (трех сторон и трех углов) по трем известным элементам (сторонам и углам). В статье Треугольники. Признаки равенства треугольников рассматриваются условия, при которых два треугольника оказываются равными друг друга. Как следует из статьи, треугольник однозначно определяется тремя элементами. Это:
- Три стороны треугольника.
- Две стороны треугольника и угол между ними.
- Две стороны и угол противостоящий к одному из этих сторон треугольника.
- Одна сторона и любые два угла.
Заметим, что если у треугольника известны два угла, то легко найти третий угол, т.к. сумма всех углов треугольника равна 180°.
- Решение треугольника по трем сторонам
- Решение треугольника по двум сторонам и углу между ними
- Решение треугольника по стороне и любым двум углам
- Сумма углов треугольника — определение и вычисление с доказательствами и примерами решения
- Калькулятор сторон и углов треугольника
- Как решить треугольник
- Примеры решений практических задач
- Треугольники
- Свойства треугольников
- Радиус вписанной окружности
- Радиус описанной окружности
- 📹 Видео
Видео:№224. Найдите углы треугольника ABC, если ∠A:∠B:∠C= 2:3:4.Скачать

Решение треугольника по трем сторонам
Пусть известны три стороны треугольника a, b, c (Рис.1). Найдем 
 |
 |
 |
 | (1) |
 | (2) |
Из (1) и (2) находим cosA, cosB и углы A и B (используя калькулятор). Далее, угол C находим из выражения
 . . |
Пример 1. Известны стороны треугольника ABC: 

Решение. Из формул (1) и (2) находим:
  . . |
  . . |
 , ,  . . |
И, наконец, находим угол C:
  |
Видео:7 класс, 31 урок, Теорема о сумме углов треугольникаСкачать

Решение треугольника по двум сторонам и углу между ними
Пусть известны стороны треугольника a и b и угол между ними C (Рис.2). Найдем сторону c и углы A и B.
 |
Найдем сторону c используя теорему косинусов:
 . . |
 . . |
Далее, из формулы
 . . |
 . . | (3) |
Далее из (3) с помощью калькулятора находим угол A.
Поскольку уже нам известны два угла то находим третий:
 . . |
Пример 2. Известны две стороны треугольника ABC: 

Решение. Иcпользуя теорму косинусов найдем сторону c:
 , , |
   . . |
Из формулы (3) найдем cosA:
  |
 . . |
Поскольку уже нам известны два угла то находим третий:
  . . |
Видео:№223. Найдите угол С треугольника ABC, если: a) ∠A=65°, ∠B = 57°; б) ∠A = 24°, ∠B= 130Скачать
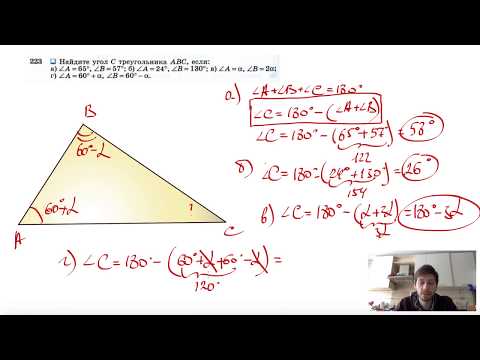
Решение треугольника по стороне и любым двум углам
Пусть известна сторона треугольника a и углы A и B (Рис.4). Найдем стороны b и c и угол C.
 |
Так как, уже известны два угла, то можно найти третий:
 . . |
Далее, для находждения сторон b и c воспользуемся тероемой синусов:
 , ,  . . |
 , ,  . . |
Пример 3. Известна одна сторона треугольника ABC: 

Решение. Поскольку известны два угла, то легко можно найти третий угол С:
  |
Найдем сторону b. Из теоремы синусов имеем:
 |
 |
Найдем сторону с. Из теоремы синусов имеем:
Видео:№228. Найдите углы равнобедренного треугольника, если один из его углов равен: а) 40°Скачать

Сумма углов треугольника — определение и вычисление с доказательствами и примерами решения
Сумма углов треугольника:
Великий французский ученый XVII в. Блез Паскаль (1623—1662) еще в детстве любил изучать геометрические фигуры, открывать их свойства, измерять углы транспортиром.
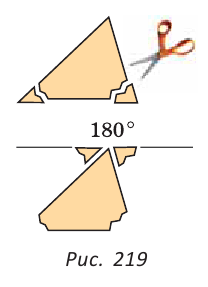
Юный исследователь заметил, что у любого треугольника сумма углов одна и та Ж6 180°. «Как же это объяснить?» — думал Паскаль. Тогда он отрезал у треугольника два уголка и приложил их к третьему (рис. 219). Получился развернутый угол, который, как известно, равен 180°. Это было его первое собственное открытие! Дальнейшая судьба мальчика была предопределена.
Теорема. Сумма углов треугольника равна 180°.
Дано: 
Доказать: 
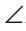
Доказательство:
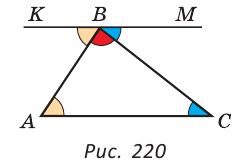
Через вершину В треугольника ABC проведем прямую КМ, параллельную стороне АС. Тогда 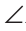
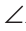
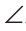
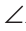
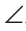





Следствия.
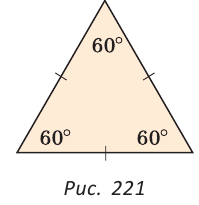
1. Каждый угол равностороннего треугольника равен 60°. (рис. 221).
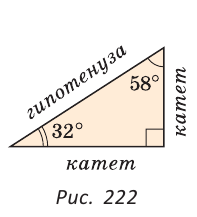
2. Сумма острых углов прямоугольного треугольника равна 90° (рис. 222).
В прямоугольном треугольнике стороны, заключающие прямой угол, называются катетами, сторона, противолежащая прямому углу, — гипотенузой (см. рис. 222).
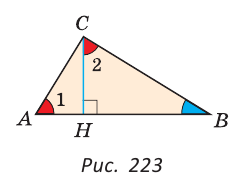
Проведем в прямоугольном треугольнике ABC высоту СН к гипотенузе АВ (рис. 223). Так как в треугольнике ABC угол 1 дополняет угол В до 90°, а в треугольнике СНВ угол 2 также дополняет угол В до 90°, то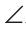
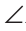
Доказано свойство: «Угол между высотой прямоугольного треугольника, проведенной к гипотенузе, и катетом равен углу между другим катетом и гипотенузой».
Пример:
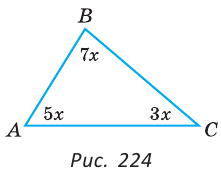
В треугольнике ABC градусные меры углов А, В и С относятся соответственно как 5:7:3. Найти углы треугольника (рис. 224).
Решение:
Пусть 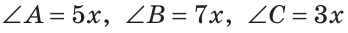
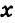
Так как сумма углов треугольника равна 180°, то
Тогда
Ответ:
Пример:
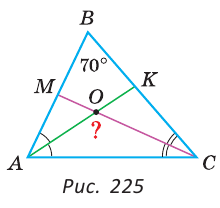
В треугольнике ABC (рис. 225) угол В равен 70°, АК и СМ — биссектрисы, О — точка их пересечения. Найти угол АОС между биссектрисами.
Решение:
Сумма углов А и С треугольника ABC равна 180° — 70° = 110°. Так как биссектриса делит угол пополам, то
Из треугольника АОС находим:
Замечание. Если 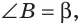
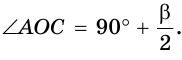
Пример:
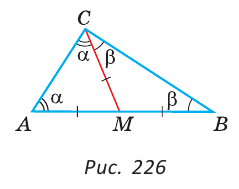
Доказать, что если медиана треугольника равна половине стороны, к которой она проведена, то данный треугольник — прямоугольный.
Доказательство:
Пусть СМ — медиана, 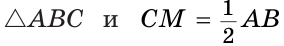
Докажем, что
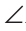

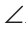






















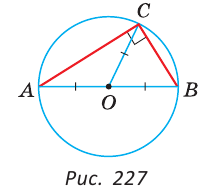
Замечание. Угол, вершина которого лежит на окружности, а стороны пересекают окружность, называется вписанным. На рисунке 227 это угол АСВ. Из задачи 3 следует свойство: «Вписанный угол, опирающийся на диаметр, — прямой».
Пример:
Доказать, что в прямоугольном треугольнике медиана, проведенная к гипотенузе, равна половине гипотенузы.
Доказательство:
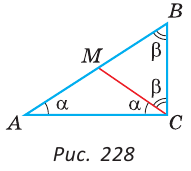
Пусть в треугольнике ABC (рис. 228) 




Проведем отрезок СМ так, что










| Рекомендую подробно изучить предметы: |
|
| Ещё лекции с примерами решения и объяснением: |
- Внешний угол треугольника
- Свойство точек биссектрисы угла
- Свойство катета прямоугольного треугольника, лежащего против угла в 30°
- Четырехугольник и его элементы
- Перпендикулярные прямые в геометрии
- Признаки равенства треугольников
- Признаки равенства прямоугольных треугольников
- Соотношения в прямоугольном треугольнике
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
Видео:Внешний угол треугольникаСкачать

Калькулятор сторон и углов треугольника
Треугольник ΔABC,
a = BC, b = AC, c = AB — стороны треугольника,













Как пользоваться онлайн-калькулятором. В форме укажите три значения: одну сторону и 2 дополнительных параметра (например, угол и сторону, два угла или две стороны). Заполните поле «Текст с картинки». Нажмите «Решить».
Калькулятор треугольника нужен, если требуется найти решение треугольников – длины сторон и величину углов треугольника.
Решить треугольник − найти все углы и стороны треугольника. Данный калькулятор предназначен для нахождения элементов треугольника.
Видео:№1049. Найдите углы треугольника с вершинами А (-1; √3), В(1;-√3 )Скачать

Как решить треугольник
Здесь размещен онлайн-калькулятор, с помощью которого можно решить треугольник по трем, двум сторонам и углам, по теореме синусов и косинусов, то есть показывается, как находить углы в треугольнике.
Решение треугольников можно находить с помощью таблицы Брадиса. Здесь ответ вычисляется автоматически компьютерной программой онлайн, быстро и удобно.
Если нужны формулы и решения задач на теоремы косинусов и синусов с ответами, то можно найти подробное и точное решение, если использовать бесплатный калькулятор треугольника.
В решении подробно показывается, как найти третью сторону по двум сторонам и углу между ними или как определить неизвестные стороны треугольника, если известна одна сторона.
Видео:Сумма углов треугольника. Геометрия 7 класс | МатематикаСкачать

Примеры решений практических задач
1) решить треугольник по двум сторонам и противолежащему углу, т.е. углу между ними. Даны стороны а = 12 см, b = 8 см, угол=60°. Для того, чтобы решить задачу, требуется указать в онлайн-форме на данной странице условия задачи. В поле для стороны «a» указывается 12, в поле для стороны «b» ставится 8, в поле для углов «A» указывается 60. Нажать «Решить».
В ходе решения задачи получаем ответ:
сторона c = 13,8 см;
угол B = 35,2644° = 35°15’52» = 35°16′ = 0,1959π = 0,6155 rad;
угол C = 84,7356° = 84°44’8» = 84°44′ = 0,4708π = 1,4789 rad;
Периметр = 33,8 см;
Полупериметр = 16,9 см;
Площадь = 47,7984 см 2 ;
Высота ha = 7,9664 см;
Высота hb = 11,9496 см;
Высота hc = 6,9273 см;
Медиана ma = 9,5513 см;
Медиана mb = 12,2958 см;
Медиана mc = 7,5107 см;
Радиус окружности R, описанной около треугольника = 6,9291 см;
Радиус окружности r, вписанной в треугольник = 2,8283 см.
Таким образом, был найден угол треугольника по двум сторонам и углу.
2) как найти угол треугольника, зная его стороны или решите треугольник по трем сторонам. Даны три стороны a = 2 см, b = 3 см, c = 4 см. В поле онлайн-формы «a» ставим 2, в поле «b» указываем 3, в поле «c» ставим 4. Далее следует нажать «Решить».
Используя теорему косинусов, получаем
угол A = 28,955° = 28°57’18» = 28°57′ = 0,1609π = 0,5054 rad;
угол B = 46,5675° = 46°34’3» = 46°34′ = 0,2587π = 0,8128 rad;
угол C = 104,4775° = 104°28’39» = 104°29′ = 0,5804π = 1,8235 rad;
Периметр = 9 см;
Полупериметр = 4,5 см;
Площадь = 2,9046 см 2 ;
Высота ha = 2,9046 см;
Высота hb = 1,9364 см;
Высота hc = 1,4523 см;
Медиана ma = 3,3912 см;
Медиана mb = 2,7839 см;
Медиана mc = 1,5811 см;
Радиус окружности R, описанной около треугольника = 2,0657 см;
Радиус окружности r, вписанной в треугольник = 0,6455 см.
Таким образом, были найдены все углы треугольника.
3) решить треугольник по двум углам и стороне. В треугольнике ABC сторона a = 5 см, два угла B = 30°, C = 45°.
Ответ:
сторона b = 2,59 см;
сторона c = 3,66 см;
угол A = 105° = 0,5833π = 1,8326 rad;
Периметр = 11,25 см;
Полупериметр = 5,625 см;
Площадь = 4,5785 см 2 ;
Высота ha = 1,8314 см;
Высота hb = 3,5355 см;
Высота hc = 2,5019 см;
Медиана ma = 1,9488 см;
Медиана mb = 4,1857 см;
Медиана mc = 3,537 см;
Радиус окружности R, описанной около треугольника = 2,588 см;
Радиус окружности r, вписанной в треугольник = 0,814 см.
Видео:В треугольнике ABC углы А,В и С относятся как 1 :1:7 .Найти углы треугольника ABC.7 кл.ОгэСкачать

Треугольники




Треугольники бывают разными. Название треугольников зависит от длины его сторон и величины его углов.
Стороны треугольника
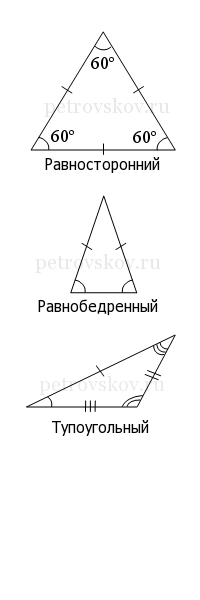
Равносторонний или правильный треугольник состоит из трех равных сторон и трех равных углов. Все три угла в равностороннем треугольнике равны 60 градусам. 
Если в треугольнике две стороны имеют одинаковую длину, то это равнобедренный треугольник.
В равнобедренном треугольнике две равные стороны называются боковыми сторонами, а третья сторона называется основанием треугольника.
Теоремы равнобедренных треугольников:
1) углы при основании равны,
2) если в треугольнике два угла равны, то это равнобедренный треугольник,
3) медиана, которая проведена к основанию, является биссектрисой и высотой.
Равные стороны в треугольниках обозначают одним, двумя или тремя штрихами или черточками, равные углы – одной, двумя или тремя дуговыми линиями.
Углы треугольника
Треугольники бывают остроугольными, тупоугольными и прямоугольными.
Треугольник является прямоугольным, если один из трех углов треугольника равен 90 градусам. Сторона, которая расположена напротив угла в 90 градусов, называется гипотенузой. Гипотенуза – самая большая сторона в прямоугольном треугольнике. Две другие стороны называются катетами.
Тупоугольный треугольник – треугольник, в котором один из углов больше 90 градусов.
Остроугольный треугольник – треугольник, в котором все три угла меньше 90 градусов.
Видео:№236. Сравните углы треугольника ABC и выясните, может ли быть угол А тупым, если: а) АВСкачать
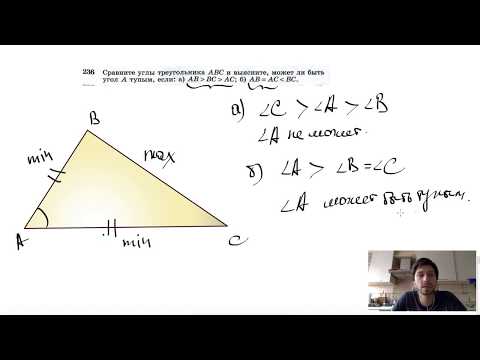
Свойства треугольников
В треугольнике только один угол может быть больше 90 градусов.
В треугольнике сумма углов равна 180 градусам.
Внешний угол треугольника – смежный угол при этой вершине.
Варианты, как найти внешний угол при вершине:
а) суммировать два внутренних угла, не смежных с ним,
б) вычислить разность между 180 и внутренним углом этой вершины.
Если сложить любые две стороны треугольника, то сумма длин этих сторон всегда больше длины третьей стороны.
Видео:№234. Один из внешних углов равнобедренного треугольника равен 115°. Найдите углы треугольника.Скачать

Радиус вписанной окружности
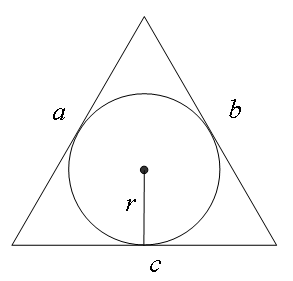
Окружность, вписанная в треугольник, – это круг, расположенный внутри треугольника. 
Радиус этого круга (r) – отрезок, проведенный из центра вписанной окружности перпендикулярно к одной из сторон треугольника.
Центр вписанной окружности – точка пересечения двух биссектрис и равноудален от каждой стороны треугольника.
Для вычисления радиуса вписанной окружности используются площадь и периметр треугольника
Видео:№235. В равнобедренном треугольнике ABC с основанием АС проведена биссектриса AD. Найдите углыСкачать

Радиус описанной окружности
Окружность, описанная около треугольника, проходит через 3 вершины треугольника. 
Для вычисления радиуса описанной окружности (R) используются площадь и длины всех сторон треугольника.
📹 Видео
В треугольнике ABC проведена биссектриса AD и AB=AD=CD. Найти меньший угол треугольника ABCСкачать

Задание 24 ОГЭ по математике #7Скачать

№227. Найдите углы равнобедренного треугольника, если: а) угол при основании в два разаСкачать

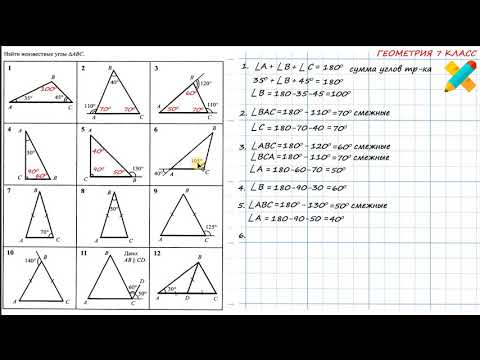
Задачи по рисункам. Найти углы треугольника АВС. Сумма углов треугольника.Скачать
Математика | Соотношения между сторонами и углами в прямоугольном треугольнике.Скачать

Только 1 может решить эту хитрую задачу ★ Найдите углы треугольника ★ Супер ЖЕСТЬСкачать

Всё про углы в окружности. Геометрия | МатематикаСкачать

Геометрия Найдите сторону AB треугольника ABC если AC = √6 см угол B = 120 угол C = 45Скачать

№230. Биссектрисы углов А и В треугольника ABC пересекаются в точке М. Найдите ∠AMBСкачать