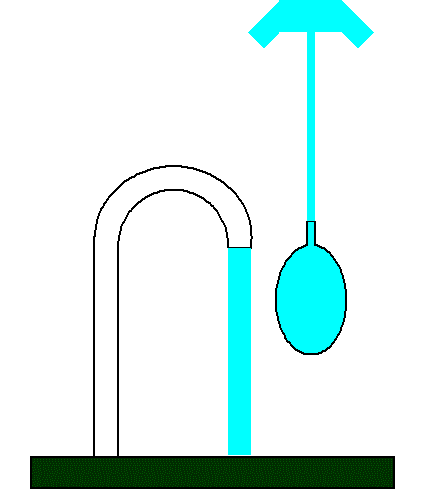- Емкость и индуктивность в электрических цепях
- Векторная диаграмма токов и напряжений
- Определение
- Разновидности
- Построение
- Способ 2
- Заключение
- Видео по теме
- Вектора емкость и индуктивность
- 3.9.2. Переменный ток, текущий через индуктивность
- 3.9.3. Переменный ток, текущий через емкость
- 3.9.4. Переменный ток, текущий через цепь с емкостью, индуктивностью и активным сопротивлением
- 3.9.5. Мощность, выделяемая в цепи переменного тока
- 3.9.6. Свободные колебания тока в электромагнитном контуре без потерь
- 3.9.7 Электромагнитные волны
- 🌟 Видео
Емкость и индуктивность в электрических цепях
Применительно к электрическим цепям, емкость и индуктивность имеют очень важное значение, не менее важное чем активное сопротивление. Но если говоря об активном сопротивлении, мы подразумеваем просто необратимое превращение электрической энергии в тепло, то индуктивность и емкость связаны с процессами накопления и преобразования электрической энергии, поэтому они открывают для электротехники многие полезные практические возможности.
Когда по цепи течет ток, заряженные частицы движутся от места с более высоким электрическим потенциалом — к месту с потенциалом более низким.
Допустим, ток проходит через активное сопротивление, например через вольфрамовую нить накала лампы. По мере движения заряженных частиц непосредственно через вольфрам, энергия данного тока непрерывно рассеивается из-за частых столкновений носителей тока с узлами кристаллической решетки металла.
Здесь можно провести такую аналогию. Валун лежал на вершине лесистой горы (в точке с высоким потенциалом), но вот его подтолкнули с вершины, и он покатился в низину (к уровню более низкого потенциала) через лес, через кусты (активное сопротивление) и т. д.
Сталкиваясь с растениями, валун систематически теряет свою энергию, передает ее кустам и деревьям в моменты столкновений с ними (подобным образом рассеивается тепло на активном сопротивлении), его скорость (величина тока) поэтому ограничена, он просто не успевает как следует разогнаться.
В нашей аналогии валун — это электрический ток, движущиеся заряженные частицы, а растения на его пути — это активное сопротивление проводника; перепад высот — разность электрических потенциалов.
Емкость же, в отличие от активного сопротивления, характеризует способность цепи накапливать электрическую энергию в форме статического электрического поля.
Постоянный ток не может продолжать идти как прежде через цепь, обладающую емкостью, пока данная емкость целиком не заполнится. Только когда емкость заполнится — носители заряда смогут двинуться дальше со своей прежней скоростью, определяемой разностью потенциалов и активным сопротивлением цепи.
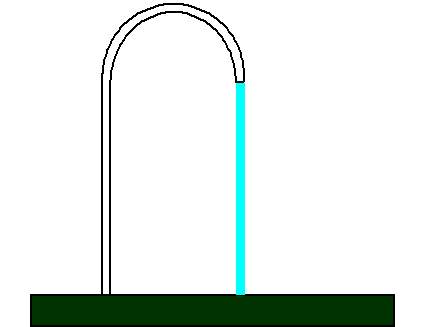
Здесь для понимания лучше подойдет наглядная гидравлическая аналогия. Водопроводный кран присоединен к водопроводу (источник тока), кран открыт, и вода с определенным напором вытекает, падает на землю. Здесь нет никакой дополнительной емкости, расход воды (величина тока) постоянен и нет причин для замедления воды, то есть для уменьшения скорости ее расхода.
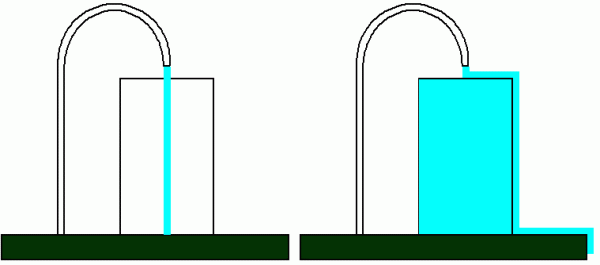
Но что если прямо под кран поставить широкую бочку (в нашей аналогии — добавить в цепь емкость, конденсатор), ее ширина значительно больше диаметра струи воды.
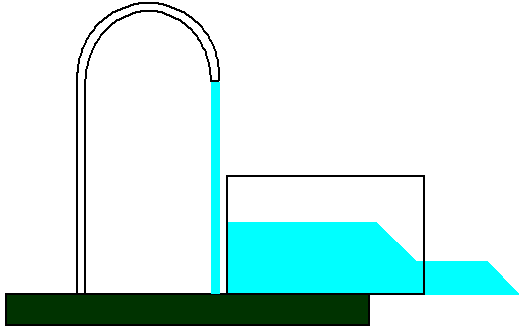
Теперь наполняется бочка (заряжается емкость, заряд накапливается на обкладках конденсатора, между обкладками усиливается электрическое поле), а на землю вода не попадает. Когда же бочка заполнится водой до краев (конденсатор зарядится), только тогда вода начнет с прежним уровнем расхода стекать через края бочки на землю. Такова роль емкости или конденсатора.
Бочку можно при желании опрокинуть, кратковременно создав многократно больший напор чем просто из крана (быстро разрядить конденсатор), однако количество воды, взятой из крана, не прибавится.
Набирая и затем опрокидывая бочку (длительно заряжая и быстро разряжая конденсатор), мы можем изменить режим расхода воды (электрического заряда, электрической энергии). Поскольку бочка наполняется водой медленно, и ее край будет достигнут через какое-то время, то говорят, что при зарядке емкости ток опережает напряжение (в нашей аналогии напряжение — это высота, на которой расположен край носика крана).
Индуктивность, в отличие от емкости, накапливает электрическую энергию не в статической, а в кинетической форме.
Когда ток течет через катушку индуктивности, заряд в ней не накапливается как в емкости, он продолжает двигаться по цепи, зато вокруг катушки усиливается связанное с током магнитное поле, индукция которого пропорциональна величине тока.
Когда к катушке приложено электрическое напряжение, ток в катушке нарастает медленно, магнитное поле запасает энергию не мгновенно, а постепенно, и этот процесс мешает носителям заряда разогнаться. Поэтому говорят, что в индуктивности ток отстает от напряжения. Однако в конце концов ток достигает такого значения, которое становится ограничено лишь активным сопротивлением цепи, в которую включена данная катушка.
Если катушку с установившимся током в какой-то момент резко отключить от цепи, ток не сможет остановиться мгновенно, однако начнет быстро замедляться, а на выводах катушки возникнет разность потенциалов тем большая, чем быстрее остановится ток, то есть чем быстрее исчезнет магнитное поле этого тока.
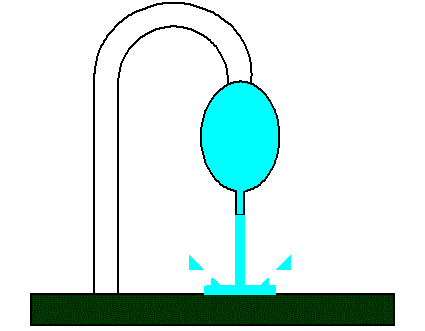
Здесь подойдет такая гидравлическая аналогия. Представим себе водопроводный кран, на носик которого надет шар из очень эластичной и мягкой резины.
Снизу на шаре есть трубочка, ограничивающая напор воды из шара на землю. Если водопроводный кран открыт, то шар довольно сильно надуется, а вода устремится через трубочку тоненькой струйкой но с большой скоростью, она будет с брызгами врезаться в землю.
Расход воды неизменен. Ток через большую индуктивность течет, при этом запас энергии в магнитном поле велик (шар надут водой). Когда вода только начинает течь из крана, шар надувается, таким же образом индуктивность запасает энергию в магнитном поле когда ток начинает усиливаться.
Если теперь отсоединить шар от крана, заткнуть его с той стороны, где он был присоединен к крану, и перевернуть, то вода из трубочки сможет достичь значительно большей высоты чем высота крана, поскольку вода в надутом шаре находится под давлением. Подобным образом индуктивности используются в повышающих импульсных преобразователях.
Видео:Цепи переменного тока с индуктивностью и емкостьюСкачать
Векторная диаграмма токов и напряжений
Процессы, протекающие в электроцепи переменного тока с активным сопротивлением и реактивной индуктивностью, можно наглядно выразить в графическом виде.
Статья даст описание, что такое векторные диаграммы, где и для чего они используются. Также будет описана временная диаграмма и ее назначение. В конце будет дан пример построения простой диаграммы для электроцепи с последовательным соединением элементов.
Видео:LC-100A измеритель ёмкости и индуктивности. Доработанный мною.Скачать

Определение
Векторная диаграмма токов и напряжений — это геометрическое изображение всех процессов, величин и амплитуд синусоидального тока. Все имеющиеся величины располагаются на плоскости в виде векторов.
Построение векторной диаграммы использует физика и электротехника. Благодаря созданию такой диаграммы можно значительно упростить выполняемые расчеты, а так же в наглядном и доступном виде отобразить происходящие процессы.
Метод векторных диаграмм позволяет также увидеть в цепи переменного тока возникающие короткие и межфазовые замыкания, а также вычислить возможные потери мощности.
Обычно такая диаграмма строится вместе с временной. Временная диаграмма — это графическое изображение входа и выхода в электрической цепи. Временные диаграммы помогают определить временной промежуток между началом, протеканием и окончанием сигнала. Например, при нажатии на кнопку возникает сигнал, который поступает к приемнику и запускает процесс его работы.
Временные диаграммы также применимы к синусоидальной электрической цепи, так как этот ток имеет начальную точку отсчета (включение питания) и время движения от источника тока к потребителю. Такие диаграммы представляют собой график, на котором изображается начальная точка отсчета, вектор времени и углы смещения фаз.
Видео:Урок 359. Конденсатор и катушка индуктивности в цепи переменного тока.Скачать

Разновидности
Разобравшись, что такое и для чего применяется векторная диаграмма, нужно узнать какие разновидности построения существуют. Они отличаются по характеру построения и типу. По характеру бывают:
- Точными. Векторная точная диаграмма — это отображение выполненного численного расчета в соответствующем масштабе. С помощью нее определяют параметры фаз и амплитудные значения строго геометрическим способом.
- Качественные. Такие гистограммы строят для наблюдения взаимосвязи между электровеличинами без использования числовых характеристик. Такой способ позволяет экспериментировать с различными параметрами и моделировать процессы в электроцепях.
Векторную диаграмму токов можно построить 2 разными способами:
- Круговым. В ее принципе лежит вектор, который описывает изменение характеристик путем образования круга или полукруга на плоскости. При таком варианте учитывается направление движения с учетом направления положения вектора.
- Линейным. Такой векторной диаграмме при изменении характеристик направление изменяется строго прямолинейно.
Оба построения могут использоваться для расчета характеристик переменного тока в цепи с сопротивлением и индуктивностью.
Видео:Емкость и индуктивность в цепи переменного тока. Физика 11 классСкачать

Построение
Построение простых векторных диаграмм будет рассмотрено в данном разделе. Для примера можно взять простую цепь с несколькими элементами и их значениями. Такая схема подразумевает последовательное соединение элементов между собой. Цепь состоит из катушки индуктивности, конденсатора и активного сопротивления. Параметры каждого элемента цепи приведены ниже.
- Катушка индуктивности UL с напряжением 15 вольт. Ток в индуктивном сопротивлении имеет сдвиг фазы 90°.
- Конденсатор UC с напряжением 20 вольт и опережением на 90 градусов.
- Напряжение резистора UR 10 вольт, его направление совпадает с током I.
- Сила тока в цепи I равняется 3 ампера.
Далее можно сделать простую диаграмму, которая поможет определить напряжение для всей схемы.
- Отложить на плоскости I в виде горизонтальной линии с масштабом 1 A/см (масштаб может быть любым, главное — выполнять все элементы диаграммы одного типа в одном масштабе). Сам ток равен 3 ампера, поэтому его длина будет равна 3 см.
- Теперь необходимо отложить вертикальный вектор UL в масштабе 5 В/см. Он отображает напряжение катушки индуктивности и равен 15 вольт. Его длина на плоскости составит в данном масштабе так же 3 см.
- Далее нужно графически обозначить вектор напряжения активного сопротивления. Его точка отсчета располагается на окончании вертикального вектора UL. Для принятого масштаба 5 В/см ему соответствует вектор длиной 2 см. Линия должна быть строго параллельна горизонтальному вектору I.
- Теперь нужно отобразить на данной диаграмме напряжение конденсатора UC. Его началом будет конечная точка вектора UR, а конец данного вектора будет расположен ниже горизонтального вектора I. В масштабе 5 В/см ему соответствует вектор длиной 4 см.
- Чтобы определить соответствующее такой схеме общение напряжение U надо будет сделать следующее. Начало вектора расположено в принятой точке отсчета, а конец его будет расположен в конечной точке вектора UC.
Поэтому если есть схема с последовательным соединением элементов, то всегда можно довольно просто построить векторную диаграмму и рассчитать общее напряжение для такой схемы.
Видео:Резистор, конденсатор, катушка индуктивности, сравнение свойств в электрических цепяхСкачать

Способ 2
Построение векторных диаграмм с учетом всех известных значений для цепи переменного тока с последовательным соединением конденсатора, резистора и катушки индуктивности. При таком построении нам так же известно напряжение самой цепи. Цепь состоит из:
- Резистора UR;
- Конденсатора UC;
- Катушки UL.
- На плоскости Im откладывается вектор UR (резистор). Его направление точно совпадает с током, поэтому это будет горизонтальная линия.
- От точки отсчета откладывается вниз вектор UC (конденсатор). Вектор откладывается под углом 90 градусов вниз, так как он имеет указанное ранее опережение 90°.
- От этой же точки отсчета откладывается вектор UL (катушка индуктивности). Ее значение откладывается ровно на 90 градусов вертикально, так как есть сдвиг фазы на 90 градусов.
Данная диаграмма может использоваться для контроля и расчета влияния всех известных параметров цепи и элементов, а также их взаимосвязи между собой.
- Показать результат сложения вектора UL и UC.
- При увеличении величины сопротивления определить разницу между напряжением и сопротивлением можно, используя новый вектор Um.
- Кроме того можно определить угол сдвига фазы φ в цепи.
Основное преимущество векторной диаграммы заключается в следующем — простое и быстрое сложение, вычитание двух параметров во время расчета электрических цепей.
Понятие о векторах и векторных диаграммах также подразумевает расчет цепи питания трехфазной сети, подключенной по методу звезды. Она строится с учетом сразу 3 отложенных векторов от 0 оси ординат. Такое построение определяет вектор от источника тока к приемнику. Строится вектор со следующими значениями:
- На оси ОХ откладываются настоящие значения величин, а на оси OY мнимые значения.
- Угловая величина обозначается как W.
- Также присутствует сам вектор Im и угол сдвига фаз φ.
Далее нужно сделать:
- На плоскости выбрать точку отсчета.
- От нее отложить вектор Im, учитывая угол сдвига фаз равный 90°.
- Длина вектора Im равна значению его напряжения и откладывается в выбранном масштабе.
Таким же образом на плоскость накладываются еще две прямые линии. Общая диаграмма покажет симметричность фаз или их сдвиг при появлении короткого замыкания. Такая диаграмма может стать примером для расчета напряжения, тока или нагрузки на каждую фазу с моделированием различных параметров.
Видео:Урок 287. Индуктивность контура (катушки). Явление самоиндукцииСкачать

Заключение
Векторные диаграммы сложны в понимании при расчете сложных цепей, с большим количеством сопротивлений и индуктивностью. Также, при расчете стоит учитывать тип соединения всех элементов, симметрию цепи и основные ее значения.
Видео:Индуктивность. Понять и почувствоватьСкачать

Видео по теме
Видео:ДЛЯ ЧЕГО НУЖНА КАТУШКА ИНДУКТИВНОСТИ? #катушка #индуктивность #электроникаСкачать

Вектора емкость и индуктивность
Закон Ома и вытекающие из него правила Кирхгофа были установлены для постоянных токов. Однако эти законы остаются справедливыми и для мгновенных значений изменяющихся во времени тока или напряжения, если их изменения происходят не слишком быстро. Электромагнитные возмущения распространяются по цепи со скоростью света с. Если за время τ = l/c, которое необходимо для передачи возмущения в самую отдаленную точку цепи l, сила тока изменяется незначительно, то мгновенные значения тока в начале и конце цепи будут практически одинаковыми. Токи, удовлетворяющие такому условию, называются квазистационарными. Для них справедливо неравенство:
где Т – период изменения тока.
При размерах цепи l
3 м τ = 10 -8 с. Таким образом, вплоть до периодов Т
10 -6 с, что соответствует частоте 10 6 Гц, токи в такой цепи можно считать квазистационарными. Ток промышленной частоты 50 Гц будет квазистационарным для цепей длиной l
Рис.3.9.1. Представление переменных токов с помощью векторных диаграмм
Мгновенные значения квазистационарного тока подчиняются закону Ома, и для него справедливы правила Кирхгофа. Пусть к зажимам сопротивления R (Рис.3.9.1), не обладающего индуктивностью или емкостью (такое сопротивление называется активным), приложено напряжение, изменяющееся со временем по закону:
| U = U m cosωt, | (3.9.2) |
где U m – амплитудное значение напряжения. При выполнении условия квазистационарности ток через сопротивление определяется законом Ома:
Здесь введено обозначение амплитудного значения тока:
Удобно при описании переменных токов использовать векторные диаграммы. Выберем произвольное направление, которое назовем осью токов. Отложим вдоль этого направления вектор тока длиной I m. Поскольку напряжение и ток в данном случае изменяются во времени синхронно, вектор напряжения также будет направлен вдоль оси токов. Его длина равна RI m .
3.9.2. Переменный ток, текущий через индуктивность
Рис.3.9.2. Переменный ток, текущий через индуктивность
Подадим переменное напряжение на концы индуктивности L с пренебрежимо малыми сопротивлением и емкостью (Рис.3.9.2). Через индуктивность будет течь переменный ток, вследствие чего возникнет ЭДС самоиндукции:
Используя второе правило Кирхгофа, можем записать:
В данном случае все напряжение приложено к индуктивности. Следовательно, величина
и есть падение переменного напряжения на индуктивности.
Перепишем уравнение (3.9.6) в виде:
Интегрируя (3.9.8), получим:
Постоянный ток в данном примере отсутствует, поэтому const = 0. Следовательно, имеем:
Из сопоставления (3.9.11) и (3.9.4) следует, что роль сопротивления в цепи с индуктивностью играет величина:
| X L = ωL, | (3.9.12) |
которую называют реактивным индуктивным сопротивлением.
Как видно из (3.9.12), величина индуктивного сопротивления растет при увеличении частоты тока. Постоянному току индуктивность сопротивления не оказывает.
Используя (3.9.6) и (3.9.11), падению напряжения на индуктивности можно придать вид:
Из сравнения (3.9.13) и (3.9.10) следует, что между током и напряжением в цепи с индуктивностью существует сдвиг фаз на 90 0 , причем ток отстает по фазе от напряжения. На векторной диаграмме это обстоятельство можно отразить как на Рис.3.9.2б.
3.9.3. Переменный ток, текущий через емкость
Рис.3.9.3. Ток и напряжение в цепи с емкостью
Пусть переменное напряжение подано на емкость С (Рис.3.9.3) Индуктивностью и сопротивлением подводящих проводов пренебрегаем. Емкость непрерывно перезаряжается, благодаря чему через нее протекает переменный ток. Напряжение на конденсаторе можно считать равным внешнему напряжению:
Умножая (3.9.14) на С и дифференцируя по времени, получим ток:
Величина Х С в цепи с емкостью играет роль сопротивления и называется реактивным емкостным сопротивлением.
Для постоянного тока Х С = ±, так как постоянный ток течь через конденсатор не может. Переменный ток через конденсатор проходит, причем сопротивление току тем меньше, чем больше частота.
Заменив в соотношении (3.9.14) амплитуду напряжения, используя (3.9.16), имеем:
Сравнив (3.9.17) и (3.9.15), можно сделать вывод, что между током и напряжением в цепи с емкостью существует сдвиг фаз на 90 0 , причем ток опережает по фазе напряжение. На векторной диаграмме это обстоятельство можно отразить как на Рис. 3.9.3б.
3.9.4. Переменный ток, текущий через цепь с емкостью, индуктивностью и активным сопротивлением
Рис.3.9. 4. Цепь с индуктивностью, емкостью и активным сопротивлением
Рассмотрим цепь, включающую в себя активное сопротивление, индуктивность и емкость (Рис.3.9.4). Подадим на эту цепь переменное напряжение с частотой ω . В цепи возникнет переменный ток с той же частотой. Он вызовет падение напряжения на активном сопротивлении U R . Фаза этого напряжения совпадает с фазой тока, поэтому вектор напряжения откладывают вдоль оси токов. Падение напряжения на индуктивности U L опережает ток по фазе на 90 0 , поэтому вектор, изображающий U L , должен быть повернут относительно оси токов на 90 0 против часовой стрелки. Наконец, падение напряжения на емкости U С отстает по фазе от тока на 90 0 и должно быть изображено вектором U С , повернутым относительно оси токов на 90 0 по часовой стрелки.
Сложив векторы, изображающие U L , U R и U С , получим вектор, изображающий приложенное напряжение U. Его длина равна U m . Этот вектор образует с осью токов угол φ, тангенс которого можно вычислить из Рис.3.9.4:
Угол φ дает разность фаз между напряжением U и силой тока i. Из Рис.3.9.4 следует также, что:
Итак, если напряжение на зажимах цепи изменяется по закону:
то в такой цепи будет течь ток:
называется полным сопротивлением цепи. При этом величина
носит наименование реактивного сопротивления . Поэтому формулу (3.9.23) можно представить в виде:
Ток отстает от напряжения (φ > 0) или опережает его (φ L и Х С .
Если , то φ > 0, и ток отстает от напряжения по фазе;
, то φ = 0, и ток и напряжение изменяются синфазно.
Для выполнения 3 условия необходимо, чтобы частота имела значение:
Если частота внешнего напряжения имеет значение (3.9.25), полное сопротивление цепи имеет наименьшее значение, равное:
| Z = R. | (3.9.26) |
Соответственно, сила тока будет иметь наибольшее значение. При этом падение напряжения на активном сопротивлении равно внешнему напряжению, приложенному к цепи:
| U = U R . | (3.9.27) |
Падения напряжения на индуктивности и емкости равны по амплитуде и противоположны по фазе. Это явление называется резонансом напряжений , а частота (3.9.25) – резонансной.
При ω = ω рез имеем для амплитуд напряжений на индуктивности и емкости :
Если , то падения напряжения на индуктивности и емкости будут превышать напряжение, приложенное к цепи.
Если емкость в цепи отсутствует, приложенное напряжение равно сумме напряжений на сопротивлении и индуктивности (Рис. 3.9.5):
| U = U R + U L . | (3.9.29) |
Тогда из Рис. 3.9.5 следует, что:
Эти формулы совпадут с выражениями (3.9.18) и (3.9.20) соответственно, если в последних положить , т.е. С = ± . Таким образом, отсутствие емкости в цепи означает именно условие С = ± . Действительно, постепенный переход от цепи, содержащей емкость, к цепи без емкости можно представить себе как сближение обкладок конденсатора вплоть до их полного соприкосновения. Но в этом случае расстояние между ними уменьшается, а емкость возрастает.
3.9.5. Мощность, выделяемая в цепи переменного тока
Рис.3.9.5. Векторная диаграмма для цепи с индуктивностью и сопротивлением
Мгновенное значение мощности, выделяемой в цепи, равно произведению мгновенных значений напряжения и силы тока:
| P(t) = U(t)I(t) = U m cosωt·I m cos(ωt-φ). | (3.9.31) |
соотношению (3.9.31) можно придать вид:
Практический интерес представляет среднее по времени значение Р(t), которое обозначим через Р. Так как среднее значение cos(2ωt-φ ) = 0, то выполняется:
Средняя мощность выделяется в активном сопротивлении в виде тепла. Используя векторную диаграмму Рис. 3.9.4, можно получить:
Подставляя (3.9.34) в (3.9.33) и учитывая, что , получаем:
Такую же мощность развивает постоянный ток, для которого сила тока равна величине:
Величина (3.9.36) называется действующим , или эффективным , значением силы тока. Аналогично для напряжения имеем действующее значение:
Используя (3.9.36) и (3.9.37), формулу (3.9.33) можно представить в виде:
Входящий в (3.9.38) множитель cosφ называют коэффициентом мощности . Если реактивное сопротивление Х = 0, то, согласно (3.9.34), cosφ = 1, и P = UI (выделяется максимальная мощность). При чисто реактивном сопротивлении цепи R = 0 и cosφ = 0, поэтому средняя мощность также равна нулю. В данном случае невозможно получить выделяемую мощность, отличную от нуля. В электротехнике для сокращения потерь поэтому стремятся сделать значение cosφ как можно больше.
3.9.6. Свободные колебания тока в электромагнитном контуре без потерь
В цепи, содержащей параллельно соединенные индуктивность и емкость, возникают электрические колебания. Такая цепь называется колебательным контуром (Рис.3.9.6).
Рис.3.9.6. Электромагнитные колебания в колебательном контуре
Для того, чтобы вызвать колебания, можно присоединить отключенный от индуктивности конденсатор к источнику тока, вследствие чего на обкладках возникнут разноименные заряды величиной q m (стадия 1). Между обкладками возникнет электрическое поле, энергия которого равна . Если затем отключить источник тока и замкнуть конденсатор на индуктивность, емкость начнет разряжаться, и в контуре потечет ток. В результате энергия электрического поля начнет уменьшаться, но зато возникнет все возрастающая энергия магнитного поля, обусловленная током, текущим через индуктивность. Эта энергия равна величине .
Так как считается, что активное сопротивление равно нулю, полная энергия не расходуется на нагревание и будет оставаться постоянной. Поэтому в момент, когда напряжение на конденсаторе и энергия электрического поля в нем равны нулю, энергия магнитного поля и величина тока достигают максимального значения (стадия 2).
В дальнейшем ток уменьшается и, когда заряды на обкладках конденсатора достигнут первоначальной величины, сила тока становится равной нулю (стадия 3). Отметим, что знаки зарядов на обкладках конденсатора противоположны тем, что были на начальном уровне.
Затем те же процессы протекают в обратном порядке (стадии 4 и 5), и весь цикл повторяется снова и снова. В ходе описанного процесса периодически изменяются (колеблются) заряд на обкладках, напряжение на конденсаторе, сила тока, текущего через индуктивность.
Колебаниям в контуре можно сопоставить колебания пружинного маятника.
Из сопоставления электрических и механических колебаний следует, что энергия электрического поля аналогична потенциальной энергии упругой деформации, а энергия магнитного поля аналогична кинетической энергии. Индуктивность L играет роль массы m, величина, обратная емкости С -1 , — роль коэффициента жесткости k. Наконец, заряду q соответствует смещение маятника х, а силе тока — скорость.
Во время колебаний внешнее напряжение к контуру не приложено. Поэтому падения напряжения на емкости и на индуктивности в сумме должны дать нуль:
Разделив (3.9.39) на величину L и используя выражение для тока , получим:
Если ввести обозначение:
то уравнение (3.9.40) принимает вид:
Это дифференциальное уравнение 2 порядка, известное как уравнение колебаний. Его решением является функция:
Следовательно, заряд на обкладках конденсатора изменяется по гармоническому закону с частотой, определяемой формулой (10.41). Это – собственная частота контура. Для периода колебаний из (10.41) можно получить формулу Томсона :
3.9.7 Электромагнитные волны
В процессах преобразования электрической энергии в энергию магнитного поля и обратно, происходящих в электромагнитном контуре, возникают электромагнитные колебания, обусловленные неразрывной связью между переменным магнитным и переменным электрическим полями. Максвелл теоретически вычислил, что такие электромагнитные колебания могут распространяться в свободном пространстве со скоростью света, приобретая при этом свойства электромагнитных волн (Рис.3.9.7).
Рис.3.9.7. Структура электромагнитной волны
Как видно из рисунка, векторы электрического и магнитного полей образуют с направлением распространения правовинтовую систему. В фиксированной точке пространства эти векторы изменяются со временем по гармоническому закону. Поскольку волна должна распространяться в пространстве, векторы электрического и магнитного полей должны зависеть от координаты:
Это – уравнения плоской электромагнитной волны, где
модуль волнового вектора, совпадающего с направлением распространения электромагнитной волны, ω и λ — циклическая частота и длина волны,
скорость электромагнитной волны, совпадающая со скоростью света.
Экспериментальное подтверждение теории Максвелла было сделано Г.Герцем в 1888г. Для получения волн Герц использовал изобретенный им вибратор. В колебательном контуре электрическое поле сосредоточено между обкладками конденсатора, а магнитное – внутри катушки. В окружающее пространство эти поля попасть не могут. Чтобы появилось излучение, нужно модифицировать колебательный контур, сделать его открытым. Этого можно достигнуть, увеличивая расстояние между пластинами конденсатора и между витками катушки (Рис.3.9.8). В пределе можно прийти к вибратору Герца – устройству, которое будет излучать электромагнитные волны, если через вибратор пропускать переменный электрический ток.
Рис.3.9.8. Открытый колебательный контур
© ФГОУ ВПО Красноярский государственный аграрный университет, 2015
🌟 Видео
RLC - Транзистор - Метр. Прибор для проверки конденсаторов, индуктивности, транзисторов, и др.Скачать

Построение векторных диаграмм/Треугольник токов, напряжений и мощностей/Коэффициент мощностиСкачать

➡️ КАК ВЫЧИТАТЬ ВЕКТОРЫ?Скачать

В поисках идеальной ёмкости. 1.0. Разные индуктивности.Скачать

Ёмкость. Индуктивность / Как понять электронику через гидравлику / #3Скачать

ЧТО ТАКОЕ ИНДУКТИВНОСТЬ. ИНДУКТИВНОЕ СОПРОТИВЛЕНИЕ [РадиолюбительTV 28]Скачать
![ЧТО ТАКОЕ ИНДУКТИВНОСТЬ. ИНДУКТИВНОЕ СОПРОТИВЛЕНИЕ [РадиолюбительTV 28]](https://i.ytimg.com/vi/aQJbGEVKYmE/0.jpg)
Расчёт катушки индуктивностиСкачать

Катушка индуктивности в цепи переменного токаСкачать

СКАЛЯРНОЕ УМНОЖЕНИЕ ВЕКТОРОВ ЧАСТЬ I #математика #егэ #огэ #формулы #профильныйегэ #векторыСкачать

ИНДУКТИВНОСТЬ В ЦЕПИ ПЕРЕМЕННОГО И ПОСТОЯННОГО ТОКА [РадиолюбительTV 91]Скачать
![ИНДУКТИВНОСТЬ В ЦЕПИ ПЕРЕМЕННОГО И ПОСТОЯННОГО ТОКА [РадиолюбительTV 91]](https://i.ytimg.com/vi/bt43zeRSJfk/0.jpg)
Последовательное соединение активного сопротивления, индуктивности и емкостиСкачать

Векторные диаграммы и коэффициент мощностиСкачать