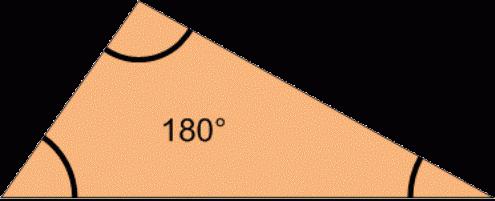
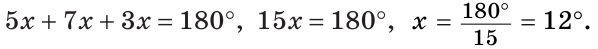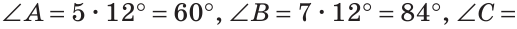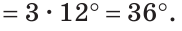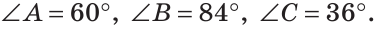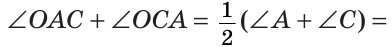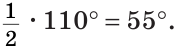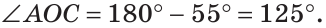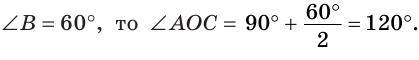Сумма углов треугольника:
Великий французский ученый XVII в. Блез Паскаль (1623—1662) еще в детстве любил изучать геометрические фигуры, открывать их свойства, измерять углы транспортиром.
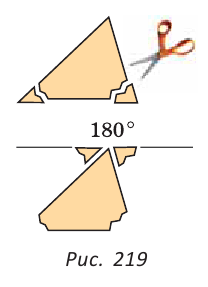
Юный исследователь заметил, что у любого треугольника сумма углов одна и та Ж6 180°. «Как же это объяснить?» — думал Паскаль. Тогда он отрезал у треугольника два уголка и приложил их к третьему (рис. 219). Получился развернутый угол, который, как известно, равен 180°. Это было его первое собственное открытие! Дальнейшая судьба мальчика была предопределена.
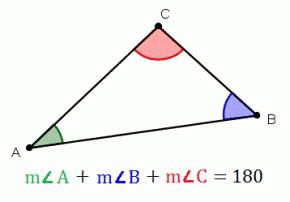
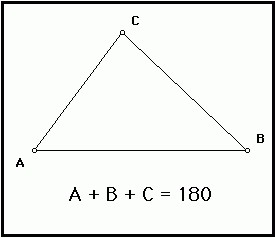
Теорема. Сумма углов треугольника равна 180°.
Дано: 
Доказать: 
Доказательство:
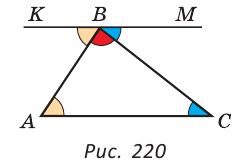
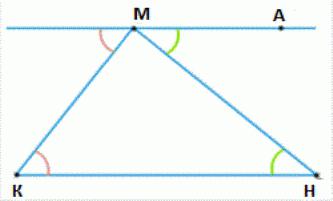
Через вершину В треугольника ABC проведем прямую КМ, параллельную стороне АС. Тогда 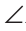
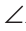
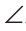
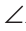





Следствия.
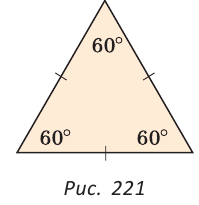
1. Каждый угол равностороннего треугольника равен 60°. (рис. 221).
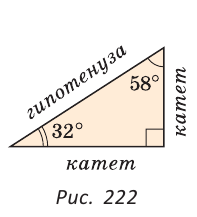
2. Сумма острых углов прямоугольного треугольника равна 90° (рис. 222).
В прямоугольном треугольнике стороны, заключающие прямой угол, называются катетами, сторона, противолежащая прямому углу, — гипотенузой (см. рис. 222).
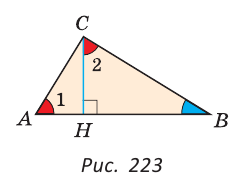
Проведем в прямоугольном треугольнике ABC высоту СН к гипотенузе АВ (рис. 223). Так как в треугольнике ABC угол 1 дополняет угол В до 90°, а в треугольнике СНВ угол 2 также дополняет угол В до 90°, то
Доказано свойство: «Угол между высотой прямоугольного треугольника, проведенной к гипотенузе, и катетом равен углу между другим катетом и гипотенузой».
Пример:
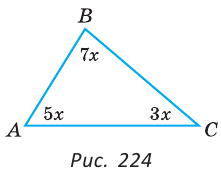
В треугольнике ABC градусные меры углов А, В и С относятся соответственно как 5:7:3. Найти углы треугольника (рис. 224).
Решение:
Пусть 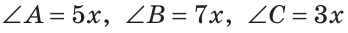
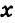
Так как сумма углов треугольника равна 180°, то
Тогда
Ответ:
Пример:
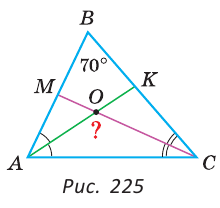
В треугольнике ABC (рис. 225) угол В равен 70°, АК и СМ — биссектрисы, О — точка их пересечения. Найти угол АОС между биссектрисами.
Решение:
Сумма углов А и С треугольника ABC равна 180° — 70° = 110°. Так как биссектриса делит угол пополам, то
Из треугольника АОС находим:
Замечание. Если 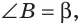
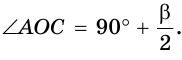
Пример:
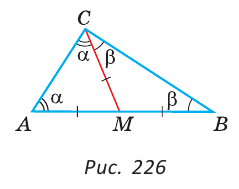
Доказать, что если медиана треугольника равна половине стороны, к которой она проведена, то данный треугольник — прямоугольный.
Доказательство:
Пусть СМ — медиана, 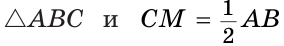
Докажем, что























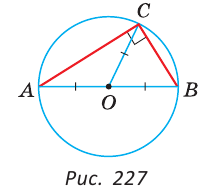
Замечание. Угол, вершина которого лежит на окружности, а стороны пересекают окружность, называется вписанным. На рисунке 227 это угол АСВ. Из задачи 3 следует свойство: «Вписанный угол, опирающийся на диаметр, — прямой».
Пример:
Доказать, что в прямоугольном треугольнике медиана, проведенная к гипотенузе, равна половине гипотенузы.
Доказательство:
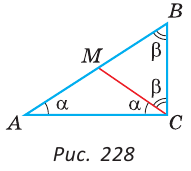
Пусть в треугольнике ABC (рис. 228) 




Проведем отрезок СМ так, что










| Рекомендую подробно изучить предметы: |
|
| Ещё лекции с примерами решения и объяснением: |
- Внешний угол треугольника
- Свойство точек биссектрисы угла
- Свойство катета прямоугольного треугольника, лежащего против угла в 30°
- Четырехугольник и его элементы
- Перпендикулярные прямые в геометрии
- Признаки равенства треугольников
- Признаки равенства прямоугольных треугольников
- Соотношения в прямоугольном треугольнике
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
- Сумма углов треугольника
- Сумма углов треугольника. Теорема о сумме углов треугольника
- Виды по величине углов
- Свойства
- Теорема о сумме углов треугольника
- Следствие
- Свойство внешних углов
- Прямоугольный треугольник
- Сумма углов равнобедренного треугольника
- Равносторонний треугольник
- Тупоугольный треугольник
- 📸 Видео
Видео:Сумма углов треугольника равна 180Скачать

Сумма углов треугольника
Сумма треугольника равна 180 градусов.
Это легко доказать. Нарисуйте треугольник. Через одну из его вершин проведите прямую, параллельную противоположной стороне, и найдите на рисунке равные углы. Сравните с решением в конце статьи.
А мы разберем задачи ЕГЭ, в которых фигурирует сумма углов треугольника.
1. Один из внешних углов треугольника равен 85 градусов. Углы, не смежные с данным внешним углом, относятся как 2:3. Найдите наибольший из них. Ответ дайте в градусах.
Внешний угол треугольника равен сумме двух внутренних углов, не смежных с ним. Следовательно, сумма двух других углов треугольника равна 85 градусов, а их отношение равно 2:3. Пусть эти углы равны 2х и 3х. Получим уравнение
2. Один из углов равнобедренного треугольника равен 98 градусов. Найдите один из других его углов. Ответ дайте в градусах.
Как вы думаете, может ли равнобедренный треугольник иметь два угла по 98 градусов?
Нет, конечно! Ведь сумма углов треугольника равна 180 градусов. Значит, один из углов треугольника равен , а два других равны .
3. На рисунке угол равен , угол равен , угол равен . Найдите угол . Ответ дайте в градусах.
Давайте отметим на чертеже еще несколько углов. Они нам понадобятся.
Сначала найдем угол .
Угол , смежный с углом равен .
Заметим, что такой способ решения — не единственный. Просто находите и отмечайте на чертеже все углы, которые можно найти.
Ты нашел то, что искал? Поделись с друзьями!
4. Углы треугольника относятся как . Найдите меньший из них. Ответ дайте в градусах.
Пусть углы треугольника равны , и . Запишем, чему равна сумма углов этого треугольника.
Как же все-таки доказать, что сумма углов треугольника равна 180 градусов? Очень просто. На нашем рисунке угол равен углу (они накрест лежащие). Угол равен углу (тоже накрест лежащие). Развернутый угол равен . Значит, и сумма углов треугольника тоже равна 180 градусов.
Видео:7 класс, 31 урок, Теорема о сумме углов треугольникаСкачать

Сумма углов треугольника. Теорема о сумме углов треугольника
Треугольник представляет собой многоугольник, имеющий три стороны (три угла). Чаще всего стороны обозначают маленькими буквами, соответствующими заглавным буквам, которыми обозначают противоположные вершины. В данной статье мы ознакомимся с видами этих геометрических фигур, теоремой, которая определяет, чему равняется сумма углов треугольника.
Видео:Почему сумма углов в треугольнике равна 180? #егэ #огэ #онлайншкола #онлайнобучение #математикаСкачать

Виды по величине углов
Различают следующие виды многоугольника с тремя вершинами:
- остроугольный, у которого все углы острые;
- прямоугольный, имеющий один прямой угол, при этом стороны, его образующие, называют катетами, а сторона, которая размещена противоположно прямому углу, именуется гипотенузой;
- тупоугольный, когда один угол тупой;
- равнобедренный, у которого две стороны равные, и называются они боковыми, а третья – основанием треугольника;
- равносторонний, имеющий все три равные стороны.
Видео:Сумма углов треугольника. Геометрия 7 класс | МатематикаСкачать

Свойства
Выделяют основные свойства, которые характерны для каждого вида треугольника:
- напротив большей стороны всегда располагается больший угол, и наоборот;
- напротив равных по величине сторон находятся равные углы, и наоборот;
- у любого треугольника есть два острых угла;
- внешний угол больше по сравнению с любым внутренним углом, не смежным с ним;
- сумма каких-либо двух углов всегда меньше 180 градусов;
- внешний угол равняется сумме остальных двух углов, которые не межуют с ним.
Видео:Почему сумма углов в треугольнике равна 180°?Скачать
Теорема о сумме углов треугольника
Теорема утверждает, что если сложить все углы данной геометрической фигуры, которая расположена на евклидовой плоскости, то их сумма будет составлять 180 градусов. Попробуем доказать данную теорему.
Пускай у нас есть произвольный треугольник с вершинами КМН.
Видео:Геометрия 7 класс (Урок№23 - Сумма углов треугольника.)Скачать

Следствие
Из выше доказанной теоремы вытекает следующее следствие: любой треугольник имеет два острых угла. Чтобы это доказать, допустим, что данная геометрическая фигура имеет всего один острый угол. Также можно предположить, что ни один из углов не является острым. В этом случае должно быть как минимум два угла, величина которых равна или больше 90 градусов. Но тогда сумма углов будет больше, чем 180 градусов. А такого быть не может, поскольку согласно теореме сумма углов треугольника равна 180° — не больше и не меньше. Вот это и нужно было доказать.
Видео:Почему сумма углов в треугольнике равна 180 градусовСкачать
Свойство внешних углов
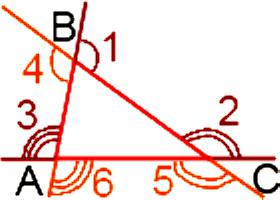
Чему равна сумма углов треугольника, которые являются внешними? Ответ на этот вопрос можно получить, применив один из двух способов. Первый заключается в том, что необходимо найти сумму углов, которые взяты по одному при каждой вершине, то есть трех углов. Второй подразумевает, что нужно найти сумму всех шести углов при вершинах. Для начала разберемся с первым вариантом. Итак, треугольник содержит шесть внешних углов – при каждой вершине по два.
Кроме этого, известно, что внешний угол у треугольника равняется сумме двух внутренних, которые не межуются с ним. Следовательно,
∟1 = ∟А + ∟С, ∟2 = ∟А + ∟В, ∟3 = ∟В + ∟С.
Из этого получается, что сумма внешних углов, которые взяты по одному возле каждой вершины, будет равна:
∟1 + ∟2 + ∟3 = ∟А + ∟С + ∟А + ∟В + ∟В + ∟С = 2 х (∟А + ∟В + ∟С).
С учетом того, что сумма углов равняется 180 градусам, можно утверждать, что ∟А + ∟В + ∟С = 180°. А это значит, что ∟1 + ∟2 + ∟3 = 2 х 180° = 360°. Если же применяется второй вариант, то сумма шести углов будет, соответственно, большей в два раза. То есть сумма внешних углов треугольника будет составлять:
∟1 + ∟2 + ∟3 + ∟4 + ∟5 + ∟6 = 2 х (∟1 + ∟2 + ∟2) = 720°.
Видео:Почему сумма углов треугольника 180? #parta #Базоваяматематика #shortsСкачать

Прямоугольный треугольник
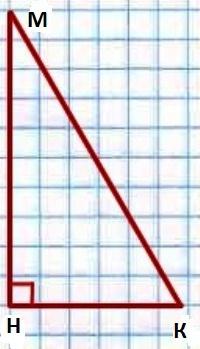
Чему равняется сумма углов прямоугольного треугольника, являющихся острыми? Ответ на этот вопрос, опять же, вытекает из теоремы, которая утверждает, что углы в треугольнике в сумме составляют 180 градусов. А звучит наше утверждение (свойство) так: в прямоугольном треугольнике острые углы в сумме дают 90 градусов. Докажем его правдивость.
Итак, согласно теореме о сумме углов ∟К + ∟М + ∟Н = 180°. В нашем условии сказано, что ∟Н = 90°. Вот и получается, ∟К + ∟М + 90° = 180°. То есть ∟К + ∟М = 180° — 90° = 90°. Именно это нам и следовало доказать.
В дополнение к вышеописанным свойствам прямоугольного треугольника, можно добавить и такие:
- углы, которые лежат против катетов, являются острыми;
- гипотенуза треугольна больше любого из катетов;
- сумма катетов больше гипотенузы;
- катет треугольника, который лежит напротив угла 30 градусов, в два раза меньше гипотенузы, то есть равняется ее половине.
Как еще одно свойство данной геометрической фигуры можно выделить теорему Пифагора. Она утверждает, что в треугольнике с углом 90 градусов (прямоугольном) сумма квадратов катетов равняется квадрату гипотенузы.
Видео:Сумма углов треугольникаСкачать

Сумма углов равнобедренного треугольника
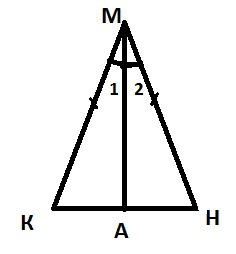
Ранее мы говорили, что равнобедренным называют многоугольник с тремя вершинами, содержащий две равные стороны. Известно такое свойство данной геометрической фигуры: углы при его основании равны. Докажем это.
Возьмем треугольник КМН, который является равнобедренным, КН – его основание.
Но нас интересует, какова сумма углов треугольника (равнобедренного). Поскольку в этом отношении у него нет своих особенностей, будем отталкиваться от теоремы, рассмотренной ранее. То есть мы можем утверждать, что ∟К + ∟М + ∟Н = 180°, или 2 х ∟К + ∟М = 180° (поскольку ∟К = ∟Н). Данное свойство доказывать не будем, поскольку сама теорема о сумме углов треугольника была доказана ранее.
Кроме рассмотренных свойств об углах треугольника, имеют место и такие немаловажные утверждения:
- в равнобедренном треугольнике высота, которая была опущена на основание, является одновременно медианой, биссектрисой угла, который находится между равными сторонами, а также осью симметрии его основания;
- медианы (биссектрисы, высоты), которые проведены к боковым сторонам такой геометрической фигуры, равны.
Видео:Почему сумма углов треугольника равна 180 #shortsСкачать

Равносторонний треугольник
Его еще называют правильным, это тот треугольник, у которого равны все стороны. А поэтому равны также и углы. Каждый из них составляет 60 градусов. Докажем это свойство.
Допустим, что у нас есть треугольник КМН. Нам известно, что КМ = НМ = КН. А это значит, что согласно свойству углов, расположенных при основании в равнобедренном треугольнике, ∟К = ∟М = ∟Н. Поскольку согласно теореме сумма углов треугольника ∟К + ∟М + ∟Н = 180°, то 3 х ∟К = 180° или ∟К = 60°, ∟М = 60°, ∟Н = 60°. Таким образом, утверждение доказано.
Существуют еще такие свойства, характерные для равностороннего треугольника:
- медиана, биссектриса, высота в такой геометрической фигуре совпадают, а их длина вычисляется как (а х √3) : 2;
- если описать вокруг данного многоугольника окружность, то ее радиус будет равен (а х √3) : 3;
- если вписать в равносторонний треугольник окружность, то ее радиус будет составлять (а х √3) : 6;
- площадь этой геометрической фигуры вычисляется по формуле: (а2 х √3) : 4.
Видео:Сумма углов любого треугольника равна 180°. | ОГЭ 2017 | ЗАДАНИЕ 13 | ШКОЛА ПИФАГОРАСкачать

Тупоугольный треугольник
Согласно определению тупоугольного треугольника, один из его углов находится в промежутке от 90 до 180 градусов. Но учитывая то, что два остальных угла данной геометрической фигуры острые, можно сделать вывод, что они не превышают 90 градусов. Следовательно, теорема о сумме углов треугольника работает при расчете суммы углов в тупоугольном треугольнике. Получается, мы смело можем утверждать, опираясь на вышеупомянутую теорему, что сумма углов тупоугольного треугольника равна 180 градусам. Опять-таки, данная теорема не нуждается в повторном доказательстве.
📸 Видео
Сумма углов остроугольного треугольника равна 180°. | ОГЭ 2017 | ЗАДАНИЕ 13 | ШКОЛА ПИФАГОРАСкачать

Почему сумма углов треугольника равна 180? #shortsСкачать

Почему сумма углов треугольника равна 180 градусам?Скачать

Чему равна сумма углов выпуклого многоугольникаСкачать

Почему сумма углов треугольника 180 градусов?Скачать

Сумма углов 180 градусовСкачать

Теорема 14.2 Если сумма односторонних углов равна 180 градусов, то прямые параллельны || Геометрия 7Скачать

Геометрия. 7 класс. Сумма углов треугольника. Внешний угол треугольника /28.01.2021/Скачать

Сумма углов равнобедренного треугольника равна 180°. | ОГЭ 2017 | ЗАДАНИЕ 13 | ШКОЛА ПИФАГОРАСкачать