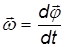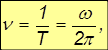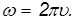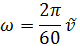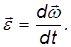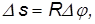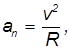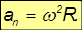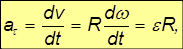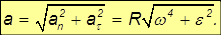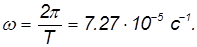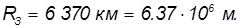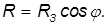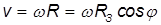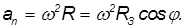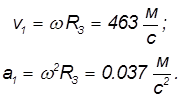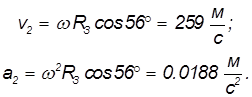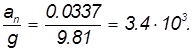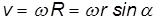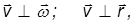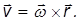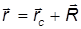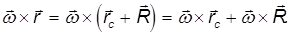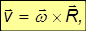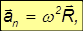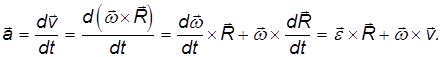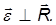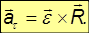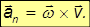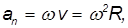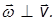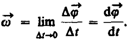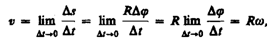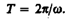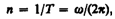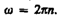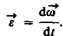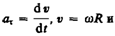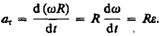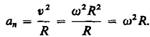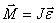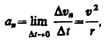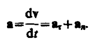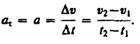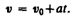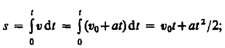Рассмотрим кинематику движения протяженного тела, размерами которого в условиях рассматриваемой задачи пренебречь нельзя. Тело будем считать недеформируемым, другими словами, — абсолютно твердым.
Движение, при котором любая прямая, связанная с движущимся телом, остается параллельной самой себе, называется поступательным.
Под прямой «жестко связанной с телом» понимается такая прямая, расстояние от любой точки которой до любой точки тела остается постоянным при его движении.
Поступательное движение абсолютно твердого тела можно охарактеризовать движением какой-либо точки этого тела, так как при поступательном движении все точки тела движутся с одними и теми же скоростями и ускорениями, а траектории их движения конгруэнтны. Определив движение какой-нибудь из точек твердого тела, мы вместе с тем определим движение всех остальных его точек. Поэтому при описании поступательного движения не возникает новых проблем по сравнению с кинематикой материальной точки. Пример поступательного движения показан на рис. 2.20.
Рис.2.20. Поступательное движение тела
Пример поступательного движения показан на следующем рисунке:
Рис.2.21. Плоское движение тела
Другой важный частный случай движения твердого тела — это движение, при котором две точки тела остаются неподвижными.
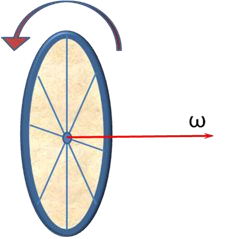
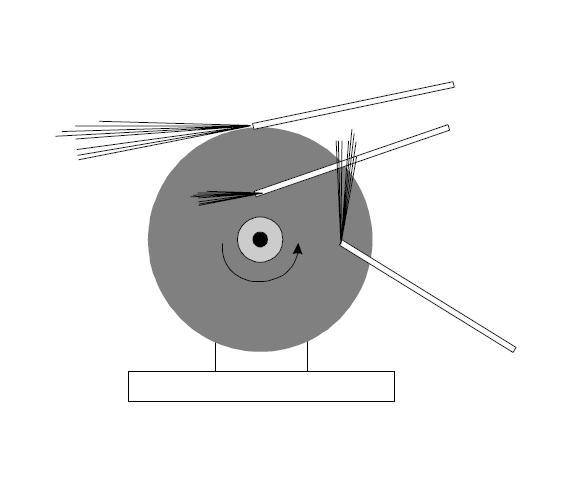
Движение, при котором две точки тела остаются неподвижными, называется вращением вокруг неподвижной оси.
Прямая, соединяющая эти точки, также неподвижна и называется осью вращения.
Рис.2.22. Вращение твердого тела
При таком движении все точки тела движутся по окружностям, расположенным в плоскостях, перпендикулярных оси вращения. Центры окружностей лежат на оси вращения. При этом ось вращения может находиться и вне тела.
Видео 2.4. Поступательное и вращательное движения.
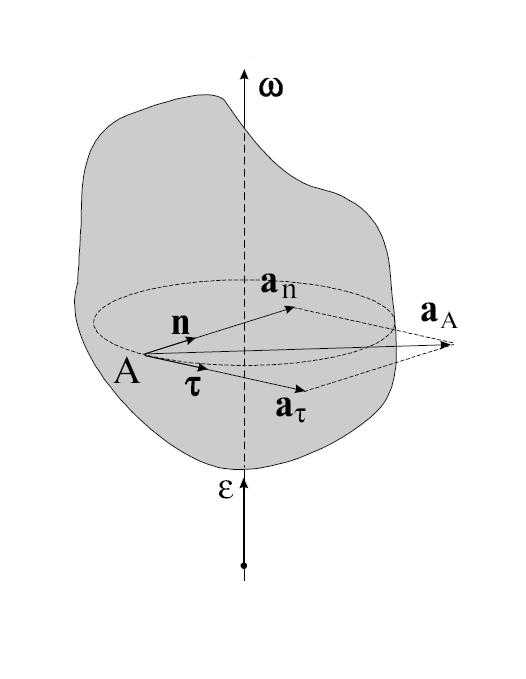
Угловая скорость, угловое ускорение. При вращении тела вокруг какой-либо оси все его точки описывают окружности различного радиуса и, следовательно, имеют различные перемещения, скорости и ускорения. Тем не менее, можно описать вращательное движение всех точек тела одинаковым образом. Для этого используют иные (по сравнению с материальной точкой) кинематические характеристики движения — угол поворота 
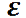
Рис. 2.23. Вектора ускорения точки, движущейся по окружности
Роль перемещения 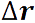
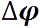
Рис. 2.24. Вращение абсолютно твердого тела вокруг неподвижной оси
Модуль вектора поворота равен величине угла поворота 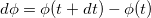
Направлен вектор бесконечно малого поворота по оси вращения в сторону движения правого винта (буравчика), вращаемого в том же направлении, что и тело.
Видео 2.5. Конечные угловые перемещения — не векторы, так как не складываются по правилу параллелограмма. Бесконечно малые угловые перемещения – векторы.
Векторы, направления которых связаны с правилом буравчика, называют аксиальными (от англ. axis — ось) в отличие от полярных. векторов, которыми мы пользовались ранее. Полярными векторами являются, например, радиус-вектор, вектор скорости, вектор ускорения и вектор силы. Аксиальные векторы называют также псевдовекторами, так как они отличаются от истинных (полярных) векторов своим поведением при операции отражения в зеркале (инверсии или, что то же самое, переходе от правой системы координат к левой). Можно показать (это будет сделано позже), что сложение векторов бесконечно малых поворотов происходит так же как и сложение истинных векторов, то есть по правилу параллелограмма (треугольника). Поэтому, если операция отражения в зеркале не рассматривается, то отличие псевдовекторов от истинных векторов никак не проявляет себя и обходиться с ними можно и нужно как с обычными (истинными) векторами.
Отношение вектора бесконечно малого поворота ко времени, за которое этот поворот имел место
называется угловой скоростью вращения.
Основной единицей измерения величины угловой скорости является рад/с. В печатных изданиях, по причинам никакого отношения к физике не имеющим, нередко пишут 1/с или с -1 , что, строго говоря, неверно. Угол — величина безразмерная, но единицы его измерения различны (градусы, румбы, грады …) и их необходимо указывать, хотя бы во избежание недоразумений.
Видео 2.6. Стробоскопический эффект и его использование для дистанционного измерения угловой скорости вращения.
Угловая скорость 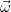
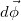
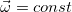
Период вращения — это время, за которое тело совершает один оборот (поворот на угол 2π) вокруг оси вращения.
Слова «достаточного постоянства» означают, очевидно, что за период (время одного оборота) модуль угловой скорости меняется несущественно.
Часто используют также число оборотов в единицу времени
При этом в технических приложениях (прежде всего, всякого рода двигатели) в качестве единицы времени общепринято брать не секунду, а минуту. То есть угловая скорость вращения 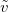

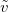
Направление вектора угловой скорости показано на рис. 2.25.
Рис. 2.25. Направление вектора угловой скорости
По аналогии с линейным ускорением вводится угловое ускорение 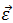
Угловое ускорение 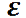
При вращении вокруг неподвижной оси, в более общем случае при вращении вокруг оси, которая остается параллельной самой себе, вектор угловой скорости также направлен параллельно оси вращения. При возрастании величины угловой скорости |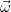
Связь угловых и линейных скоростей и ускорений. Каждая из точек вращающегося тела движется с определенной линейной скоростью 
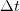
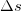
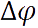
Переходя к пределу 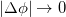
Напомним, здесь R — расстояние от рассматриваемой точки тела до оси вращения.
Рис. 2.27. Направление движения искр при заточке инструментов.
Так как нормальное ускорение равно
то с учетом соотношения для угловой и линейной скорости получаем
Нормальное ускорение точек вращающегося твердого тела часто называют центростремительным ускорением.
Дифференцируя по времени выражение для 
где 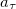
Таким образом, как тангенциальное, так и нормальное ускорения растут линейно с ростом радиуса R — расстояния от оси вращения. Полное ускорение также линейно зависит от R :
Пример. Найдем линейную скорость 
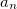
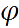
Средний радиус Земли
Расстояние до оси вращения на широте 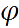
Отсюда находим линейную скорость
и центростремительное ускорение
На экваторе 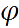
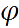
На широте Москвы cos 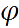
Мы видим, что влияние вращения Земли не столь велико: отношение центростремительного ускорения на экваторе к ускорению свободного падения равно
Тем не менее, как мы увидим в дальнейшем, эффекты вращения Земли вполне наблюдаемы.
Связь между векторами линейной и угловой скорости. Полученные выше соотношения между угловой и линейной скоростью записаны для модулей векторов 

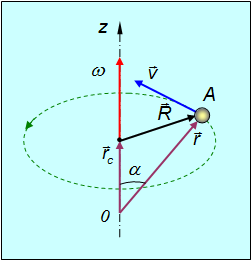
Пусть 0z — ось вращения абсолютно твердого тела (рис. 2.28).
Рис. 2.28. Связь между векторами линейной и угловой скорости
Точка А вращается по окружности радиусом R. R — расстояние от оси вращения до рассматриваемой точки тела. Примем точку 0 за начало координат. Тогда
то по определению векторного произведения, для всех точек тела
Здесь 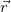
Но, с другой стороны
Первое слагаемое равно нулю, так как векторное произведение коллинеарных векторов равно нулю. Следовательно,
где вектор R перпендикулярен оси вращения и направлен от нее, а его модуль равен радиусу окружности, по которой движется материальная точка и начинается этот вектор в центре этой окружности.
Рис. 2.29. К определению мгновенной оси вращения
Нормальное (центростремительное) ускорение также можно записать в векторной форме:
причем знак «–» показывает, что оно направлено к оси вращения. Дифференцируя соотношение для линейной и угловой скорости по времени, находим для полного ускорения выражение
Первое слагаемое направлено по касательной к траектории точки на вращающемся теле и его модуль равен 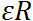
Сравнивая с выражением для тангенциального ускорения, приходим к выводу, что это — вектор тангенциального ускорения
Следовательно, второе слагаемое представляет собой нормальное ускорение этой же точки:
Действительно, оно направлено вдоль радиуса R к оси вращения и его модуль равен
Поэтому данное соотношение для нормального ускорения является другой формой записи ранее полученной формулы.
Видео:Матрица поворотаСкачать

Магия тензорной алгебры: Часть 6 — Кинематика свободного твердого тела. Природа угловой скорости
Видео:Урок 44. Вращение твердого тела. Линейная и угловая скорость. Период и частота вращения.Скачать

Введение
Что такое угловая скорость? Скалярная или векторная величина? На самом деле это не праздный вопрос.
Читая лекции по теоретической механике в университете, я, следуя традиционной методике изложения курса кинематики, вводил понятие угловой скорости в теме «Скорость точки тела при вращательном движении». И там угловая скорость впервые появляется как скалярная величина, со следующим определением.
Угловая скорость твердого тела — это первая производная от угла поворота тела по времени
А вот потом, при рассмотрении каноничной формулы Эйлера для скорости точки тела при вращении
Угловая скорость тела — это псевдовектор, направленный вдоль оси вращения тела в ту сторону, откуда вращение выглядит происходящим против часовой стрелки
Ещё одно частное определение, которое, во-первых, утверждает неподвижность оси вращения, во-вторых навязывает рассмотрение лишь правой системы координат. И наконец термин «псевдовектор» обычно объясняется студентам так: «Посмотрите, ведь мы показали, что омега — скалярная величина. А вектор мы вводим для того, чтобы выписать формулу Эйлера».
При рассмотрении сферического движения оказывается потом, что ось вращения меняет направление, угловое ускорение направлено по касательной к годографу угловой скорости и так далее. Неясности и вводные допущения множатся.
Учитывая уровень подготовки школьников, а так же вопиющую глупость, допускаемую в программах подготовки бакалавров, когда теормех начинается с первого (вдумайтесь!) семестра, такие постепенные вводные, на палках, веревках и желудях наверное оправданы.
Но мы с вами заглянем, что называется, «под капот» проблемы и, вооружившись аппаратом тензорного исчисления, выясним, что угловая скорость — это псевдовектор, порождаемый антисимметричным тензором второго ранга.
Думаю для затравки вполне достаточно, а поэтому — начнем!
Видео:Вращательное движение. 10 класс.Скачать

1. Свободное движение твердого тела. Тензор поворота
Если движение, совершаемо телом не ограничено связями, то такое его движение называют свободным
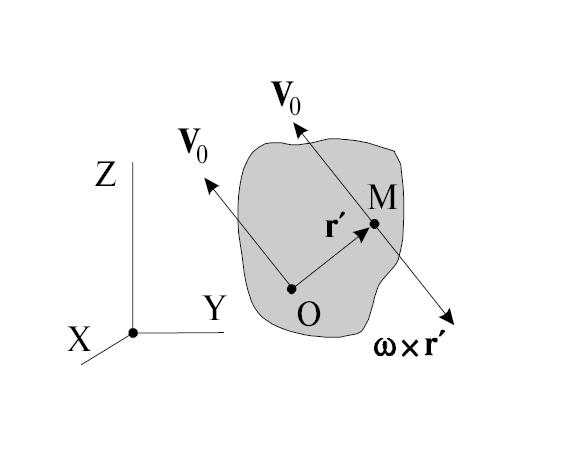
Это — самый общий случай движения тела. Следующий рисунок иллюстрирует тот факт, что свободное движение тела можно представить как сумму двух движений: поступательного вместе с полюсом и сферического вокруг полюса.
Рис. 1. Обычная иллюстрация из курса теоретической механики: определение положения свободного твердого тела в пространстве.
Напомню, что речь идет об абсолютно твердом теле, то есть теле, расстояния между точками которого не изменяется с течением времени. Ещё можно сказать, что твердое тело представляет собой неизменяемую механическую систему.
Как видно из рисунка 1, обычной практикой является рассмотрение двух систем координат — одна считается неподвижной и называется базовой, другая
жестко связанна с телом и поворачивается относительно базовой вместе с ним. Такую систему координат называют связанной.
Сначала я тоже хотел ограничиться декартовыми координатами. Но тогда бы мои читатели задали бы мне логичный вопрос — «а зачем тогда тут тензоры?». Поэтому, потратив четыре для в мучительных раздумьях и «нагуляв» окончательное решение пару часов назад, я решил замахнуться на «Вильяма, нашего, Шекспира» и изложить дальнейшие рассуждения в криволинейных координатах.
Рис. 2. Ориентация твердого тела в локальном базисе.
Пусть положение полюса задается вектором
Причем под этим вектором не следует понимать радиус-вектор, так как в криволинейных координатах такое понятие бессмысленно.
В точке O1 задан локальный репер базовой системы координат, образованный тройкой векторов . С движущимся телом связан подвижный репер
. Поворот связанного репера относительно базового можно задать линейным оператором. Получим этот оператор и исследуем его свойства
Рассмотрим некоторую точку M, принадлежащую телу. К ней из полюса можно провести вектор неподвижный относительно связанного репера. Его можно разложить по векторам этого репера
и по векторам базового репера
Каждый вектор связанного репера можно разложить через векторы базового репера
Подставляем (4) в (2) и сравниваем с (3)
Из (5) понятно, что компоненты вектора в базовой системе координат, пересчитываются через его компоненты в связанной системе путем применения линейного оператора
или в безиндексной форме
где столбцы матрицы
– контравариантные компоненты векторов связанного репера по отношению к базовому. Точка, как мы уже отмечали в прошлой статье, обозначает умножение тензоров с последующей сверткой по соседней паре индексов. Линейный оператор
действует на векторы таким образом, что поворачивает их относительно некоторой оси, не меняя длины и угла между векторами. Такое преобразование пространства называется ортогональным. Для того, чтобы таковое преобразование было возможным, оператор (7) должен обладать вполне определенными свойствами. Если длина векторов базиса и углы между ними не меняются, то это означает равенство всех попарных скалярных произведений векторов репера как в базовой, так и в связанной системах координат
Правая часть (8) — это локальный метрический тензор
Преобразование координат при повороте является тождественным для метрического тензора, то есть переводит метрический тензор сам в себя.
В выражении (10) нетрудно увидеть преобразование метрического тензора про смене системы координат, о котором мы подробно говорили в самой первой статье цикла
Стоп! Но мы же знаем, что матрицы поворота обычно ортогональны, то есть произведение матрицы поворота на её транспонированную дает единичную матрицу, иными словами, чтобы обратить матрицу поворота её достаточно транспонировать.
Но ортогональность свойственна матрицам поворота, преобразующим ортонормированный декартов базис. Здесь мы имеем дело с локальным базисом, при повороте которого должны сохранятся длины векторов и углы между ними. Если мы примем базис декартовым, то из (10) мы получим привычные свойства матрицы поворота, к примеру её ортогональность.
Для дальнейших вычислений нам потребуется знать, как будет выглядеть матрица обратного преобразования, то есть . Что же, посмотрим. Для этого умножим (10) слева на
и справа на
откуда незамедлительно получаем
Выходит, что матрица обратного преобразования действительно получается из транспонированной матрицы преобразования, но с участием метрического тензора. Выражения (10) и (11) очень пригодятся нам, а пока сделаем некоторые выводы.
Закон свободного движения твердого тела можно выписать в криволинейных координатах в виде системы уравнений
При этом (12) — закон движения полюса, а (13) — закон сферического движения тела вокруг полюса. При этом (13) — тензор ранга (1,1), называемый тензором поворота.
Видео:Угловая скорость и радианная мера углаСкачать

2. Скорость точки тела при свободном движении. Угловая скорость выходит на сцену
Вычислим скорость точки M, положение которой в связанной системе координат задается постоянными, в силу твердости тела, криволинейными координатами
Из курса теоретической механики известна формула, определяющая скорость точки тела в данном движении
где — скорость полюса;
— скорость точки вокруг полюса.
Так как все координаты, кроме (13) определены относительно базового репера, мы можем записать
Индекс в круглых скобках означает систему координат, в которой берутся компоненты (0 — базовая, 1 — связанная). Дифференцируем (15) по времени с учетом (13)
Перейдем в (16) к связанной системе координат, домножив (15) слева на
где — компонента оператора обратного преобразования
.
Теперь сравним (17) и (14). В последнем слагаемом должно вылезти векторное произведение. Вспоминая определение векторного произведения через тензор Леви-Чивиты, данное во второй статье цикла, замечаем, что на выходе оно дает ковектор, поэтому в (17) перейдем к ковариантым компонентам, домножив это выражение на метрический тензор слева
Теперь представим себе, как выглядел бы ковектор скорости точки относительно плюса, записанный через вектор угловой скорости
Видео:Формула поворота РодригаСкачать

Вектор угла поворота тела это
3)Угол поворота, угловые скорость и ускорение. Уравнение вращательного движения. Полное ускорение, центростремительное, тангенсальное. Связь вращательных их линейных величин.
Угол поворота — это физическая величина, характеризующая поворот тела, или поворот луча, исходящего из центра вращения тела, относительно другого луча, считающегося неподвижным.
Угловой скоростью называется векторная величина, равная первой производной угла поворота тела по времени:
Линейная скорость точки
Если ( 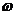
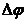
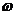
Число полных оборотов, совершаемых телом при равномерном его движении по окружности, в единицу времени называется частотой вращения:
Угловым ускорением называется векторная величина, равная первой производной угловой скорости по времени:
При вращении тела вокруг неподвижной оси вектор углового ускорения направлен вдоль оси вращения в сторону вектора элементарного приращения угловой скорости. При ускоренном движении вектор 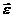
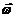
Тангенциальная составляющая ускорения
Нормальная составляющая ускорения
Основое уравнение динамики вращательного движения материальной точки — угловое ускорение точки при ее вращении вокруг неподвижной оси пропорционально вращающему моменту и обратно пропорционально моменту инерции.
Ta к как вектор скорости направлен по касательной к траектории, то вектор D v n , перпендикулярный вектору скорости, направлен к центру ее кривизны. Вторая составляющая ускорения, равная
называется нормальной составляющей ускорения и направлена по нормали к траектории к центру ее кривизны (поэтому ее называют также центростремительным ускорением).
Полное ускорение тела есть геометрическая сумма тангенциальной и нормальной составляющих (рис.5):
Итак, тангенциальная составляющая ускорения характеризует быстроту изменения скорости по модулю (направлена по касательной к траектории), а нормальная составляющая ускорения — быстроту изменения скорости по направлению (направлена к центру кривизны траектории).
В зависимости от тангенциальной и нормальной составляющих ускорения движение можно классифицировать следующим образом:
1) 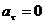
2) 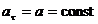
Если начальный момент времени t 1=0, а начальная скорость v 1 = v 0, то, обозначив t 2 = t и v 2 = v , получим 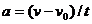
Проинтегрировав эту формулу в пределах от нуля до произвольного момента времени t , найдем, что длина пути, пройденного точкой, в случае равнопеременного движения
3) 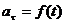
4) 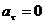
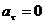
5) 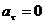
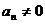
6) 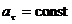
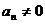
7) 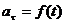
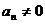
Понятно, что линейные и соответствующие им угловые величины должны быть определенным образом связаны между собой. Найдем эти связи.
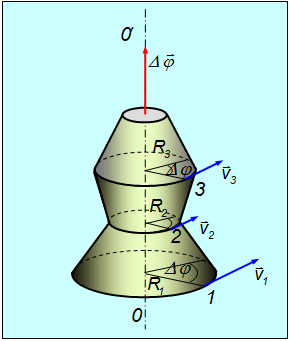
При повороте радиуса, проведенного в точку М (см. рис. 2), на угол φ точка пройдет по дуге окружности путь
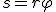
За малое время Δt точка проходит расстояние 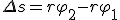
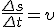
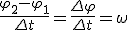
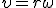
Заметим, что соотношение (2) связывает между собой линейную и угловую скорости не только при равномерном движении точки по окружности, н о- и при неравномерном движении тоже. Изменение модуля скорости точки за время Δt есть 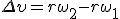
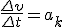
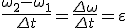
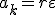
Соотношения (1), (2) и (3) дают для движущейся по окружности точки простую связь между линейными и угловыми величинами: линейная величина равна произведению радиуса окружности на соответствующую угловую величину. Эти соотношения получены нами для конкретной точки М колеса троллейбуса, но они справедливы и для любой другой точки вращающегося (как равномерно, так и неравномерно) тела.
🔍 Видео
Кинематика твёрдого телаСкачать

Лекция 10. Угловая скорость и угловое ускорение │Физика с нуляСкачать

2.4. Радиус-вектор и вектор перемещенияСкачать

Скорости и ускорения точек вращающегося телаСкачать

Лекция 4. ВЕКТОРА │ кинематика с нуляСкачать

Линейная и угловая скорости при равномерном движении по окружностиСкачать

Вращение тела вокруг неподвижной осиСкачать

Момент инерцииСкачать

Физика | Ликбез по векторамСкачать

СЕРИЯ 41 УГОЛ ПОВОРОТАСкачать

Часть 3 Поворот вектораСкачать

угловая СКОРОСТЬ формула угловое УСКОРЕНИЕ 9 классСкачать

положение тела на окружностиСкачать

ВЫЧИТАНИЕ ВЕКТОРОВ ЧАСТЬ I #егэ #огэ #математика #геометрия #профильныйегэСкачать

Урок 113. Векторное описание вращательного движения. Гироскопический эффект.Скачать