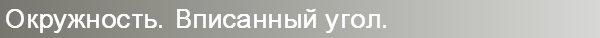Дорогие друзья! Мы уже рассматривали с вами задачи на вписанный в окружность угол. Если вы давно не решали подобных заданий, и не помните свойство вписанного угла, то обязательно ознакомьтесь с материалами и решите несколько задач, посмотрите статьи на блоге « Угол вписанный в окружность. Часть 1! » и про вписанный четырёхугольник , либо соответствующий раздел в учебной литературе.
Есть ещё один тип заданий с вписанным углом, которые входят в состав ЕГЭ. Их мы и рассмотрим в этой статье. В заданиях имеется одна особенность – окружность и угол заданы (построены) на листе в клетку и никаких градусных величин в условии не задано. Возникает вопрос: а как тогда углы-то вычислять?
Всё просто! Нужно понимать как «установить» угол, если он построен на листе в клетку, а далее использовать свойство вписанного угла. Запутал?
Начнём с самого простого. Чему равен данный угол?
Конечно же, 90 градусам.
Чему равен этот угол?
Понятно, что 45 градусам.
Правильно, 135 градусам (90 + 45 или по-другому 180 – 45).
225 градусов (180 + 45 или 360 – 135).
Понимания того, как стороны угла расположены относительно клеток вполне достаточно, чтобы решать такие задачи.
Ещё раз напомню основное свойство вписанного угла.
«Вписанный угол равен половине центрального,
опирающегося на ту же дугу»
27891. Найдите градусную величину дуги BC окружности, на которую опирается угол BAC . Ответ дайте в градусах.
Все подобные задания, в которых дан вписанный в окружность угол (либо центральный угол) на листе в клетку, решаются просто – угол определяется по расположению его сторон относительно клеток. Если необходимо, то используется свойство вписанного угла.
Построим центральный угол соответствующий дуге ВС:
Градусная величина дуги на которую опирается вписанный угол равна центральному углу опирающемуся на эту дугу, то есть нам необходимо найти угол ВОС:
По клеткам видно, что угол ВОС равен 90 0 + 45 0 = 135 0 (ОС проходит по диагонали клеток).
27887. Найдите величину угла ABC . Ответ дайте в градусах.
27888. Найдите величину угла ABC. Ответ дайте в градусах.
27889. Найдите величину угла ABC . Ответ дайте в градусах.
27890. Найдите градусную величину дуги AC окружности, на которую опирается угол ABC . Ответ дайте в градусах.
Нужно знать свойство вписанного угла (обязательно).
Для решения подобных задач достаточно построить центральный угол и далее использовать указанное свойство.
На этом всё. Успеха Вам!
С уважением, Александр Крутицких
Когда маленький Дракула не вернулся домой из школы, его мама так и подумала: «Наверное, кол поставили».
Видео:Всё про углы в окружности. Геометрия | МатематикаСкачать
Подготовка к ОГЭ. «Углы на клетках»
Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.
Видео:Углы в окружности. 16 задание ОГЭ математика 2023 | Молодой РепетиторСкачать
«Снятие эмоционального напряжения
у детей и подростков с помощью арт-практик
и психологических упражнений»
Сертификат и скидка на обучение каждому участнику
Углы на клетках
Как построить прямой угол по клеткам? Очень просто! – скажете вы. – Отметим точку, вершину угла, от неё чертим вправо или влево луч, затем ещё один луч вверх или вниз. Угол между горизонталью и вертикалью – прямой. А можно и по диагоналям соседних клеток.
Всё верно. А если один из лучей уже построен и он не горизонтальный, не вертикальный и не проходит по диагоналям клеток? Как начертить второй луч, чтобы угол между ними был прямым?
Найдём узел сетки, через который проходит начерченный луч. На нашем рисунке до такого узла от начала луча нужно пройти 3 клетки ВЛЕВО и 1 клетку ВНИЗ. Поэтому чтобы получился прямой угол, надо от начала луча отсчитать 1 клетку ВЛЕВО и 3 клетки ВВЕРХ. Почему? Обозначим упомянутые нами точки – А, В и О. Построим векторы ОА и ОВ. Координаты вектора ОА равны (-3; -1), вектора ОВ (-1; 3). Их скалярное произведение равно 0, поэтому они перпендикулярны.
Можно отсчитывать клетки и так: 1 клетку ВПРАВО и 3 клетки ВНИЗ. Тогда вектор ОВ имеет координаты (1; -3), при этом скалярное произведение векторов ОА и ОВ также равно 0.
Вывод. Векторы с координатами ( a ; b ) и (- b ; a ), или ( a ; b ) и ( b ; — a ), — перпендикулярны.
Рассмотрим несколько задач, связанных с умением находить прямой угол на рисунке.
№ 1 . Найти угол АВС на рисунке.
Решение. На первом рисунке угол АОС построен на диагоналях соседних клеток. На втором рисунке векторы ОА и ОС имеют координаты соответственно (3; -4) и (4; 3). Поэтому на первом и втором рисунках центральный угол АОС – прямой, а вписанный угол АВС, опирающийся на ту же дугу, равен его половине, то есть 45 ° . На третьем рисунке угол АОС – половина прямого, то есть 45 ° , а угол АВС соответственно равен 22,5 ° .
№ 2. Три квадрата расположены так, как показано на рисунке. Чему равен угол между прямыми АС и В D ?
Решение. Отрезок В D переместим параллельно вниз на одну клетку. Появляется отрезок АМ, равный В D . Угол между прямыми АС и В D равен углу между АС и АМ на втором рисунке. Соединим отрезком точки С и М. Получается, что угол АМС – прямой и АМ = МС. Треугольник АСМ прямоугольный равнобедренный, поэтому искомый угол равен 45°.
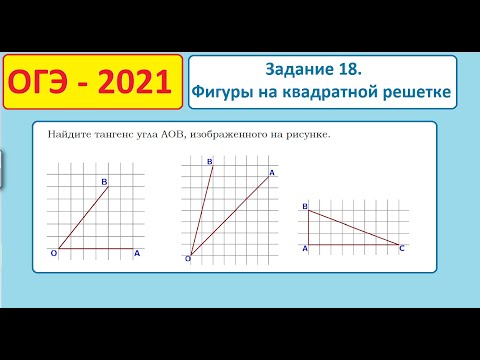
№ 3. Найти тангенс угла, изображенного на рисунке.
Решение. Выделим на этом рисунке узлы сетки – точки А и С. Рассмотрим треугольник АВС. Заметим, что он является прямоугольным, к тому же катет ВС в 2 раза больше катета АС. Отсюда следует, что тангенс угла В равен 1:2 = 0,5.
Правильный треугольник и описанная около неё окружность, построенные на клетках, несут в себе много интересных свойств. Известно, что радиус окружности, описанной около равностороннего треугольника со стороной а, равен 
, а радиус вписанной в него окружности — 
, то есть в два раза меньше. Отсюда следует, что хорда, перпендикулярная радиусу окружности и проходящая через его середину, является стороной правильного треугольника. Другими словами, острый вписанный угол, опирающийся на хорду, перпендикулярную радиусу и проходящую через его середину, равен 60 ° , а центральный угол и тупой вписанный угол, опирающиеся на эту хорду, — 120 ° .
Рассмотрим несколько примеров задач, решаемых на основе этого свойства.
Угол АВС на рисунке равен 60 ° , так как хорда АС проходит через середину радиуса и перпендикулярна ему.
Угол АВС на рисунке является половиной угла в 60 ° из предыдущей задачи и равен 30 ° .
Угол АВС на следующем рисунке равен 120 ° . При этом четырёхугольник АВСО является ромбом и его острый угол равен 60 °.
Полезным при решении задач на клетках является знание углов правильных многоугольников . Рассмотрим правильный шестиугольник и правильный восьмиугольник. Около них описаны окружности. Каждый внутренний угол правильного шестиугольника равен 120 ° , угол между диагоналями-диаметрами равен 60 ° , угол между двумя соседними диагоналями, исходящими из одной вершины, равен 30 ° , меньшая диагональ правильного шестиугольника перпендикулярна его стороне, а с другими соседними сторонами — угол 30 ° . Каждый угол правильного восьмиугольника равен 135 °, угол между соседними диагоналями-диаметрами равен 45°.
Найдите на следующих рисунках градусные меры отмеченных углов.
Видео:ОГЭ 2021. Задание 18. Фигуры на квадратной решеткеСкачать
Найти угол в окружности по клеточкам огэ
Задание 7. На клетчатой бумаге с размером клетки 1х1 изображён вписанный в окружность угол ABC . Найдите его градусную величину.
Угол ABC является вписанным углом, градусная мера которого, в 2 раза меньше градусной меры дуги, на которую он опирается, т.е. градусной меры дуги AC. В свою очередь, на дугу AC опирается центральный угол (см. рисунок), величина которого 90 градусов (видно из рисунка). Тогда градусная мера дуги также будет 90 градусов и угол ABC равен 90:2=45 градусов.
🎥 Видео
Задача на окружности из ОГЭ-2023!! Разбор за 30 секСкачать
Как решать задания на окружность ОГЭ 2021? / Разбор всех видов окружностей на ОГЭ по математикеСкачать
ОГЭ 2023 - НАЙТИ ПЛОЩАДЬ СЕКТОРА ПО УГЛУ // Окружность // Номер 16 // МатематикаСкачать
#11 Самое сложное задание 18 ОГЭ 2021. Углы на клетчатой бумаге. Вписанный угол. Тангенс угла.Скачать
ОГЭ 2019. Задание 17. Разбор задач. Геометрия. Окружность.Скачать
Ты точно получишь 1 балл по геометрии за это задание. Все типы задания №18 на ОГЭ по математике!Скачать
Углы в окружности 🔥Полезный файл забирай в комментарияхСкачать
ОГЭ I Углы в окружности I Задание 16Скачать
Углы, вписанные в окружность. 9 класс.Скачать
ОГЭ 2020. Геометрия 1 часть. Углы в окружности.Скачать
ОГЭ 2022. Все задания 16 (бывшие 17) Геометрия. Окружность. Углы в окружности.Скачать
Лайфхаки ОГЭ — площадь сектора #огэ #математикаСкачать
ОГЭ 2021. Фигуры на квадратной решетке.Скачать
Касательные к окружности с центром O в точках A и B ... | ОГЭ 2017 | ЗАДАНИЕ 10 | ШКОЛА ПИФАГОРАСкачать
Задание 16 из ОГЭ. Найдите длину большей дуги.Скачать
ОГЭ 2018. Задание 17. Окружность. Центральный и вписанный угол.Скачать
Окружности и углы. Открытый банк ОГЭ #19🔴Скачать
