Группа симметрий правильного треугольника (6 видео)

«Бесполезное» представление, преобразовавшее математику

Содержание

Изначально от теории представлений отказались. Сегодня она играет важнейшую роль в большинстве областей математики.
Группы самосовмещений многоугольников и многогранников
Теория конечных групп симметрий
🎥 Видео

Изначально от теории представлений отказались. Сегодня она играет важнейшую роль в большинстве областей математики.

Когда в конце XIX века впервые появилась теория представлений, многие математики сомневались в ценности этого подхода. В 1897 году английский математик Уильям Бёрнсайд писал, что сомневается в том, что эта необычная перспектива даст какие-то полезные результаты.

«Бёрнсайд, по сути, говорил о том, что теория представлений бесполезна», — сказал Джорди Уильямсон из Сиднейского университета в лекции 2015 года.

Прошло более ста лет после её дебюта, и теория представлений стала ключевым ингредиентом во множестве важнейших математических открытий. Однако её ценность сложно оценить с первого раза.

«Не сразу становится понятно, что её стоит изучать», — сказала Эмили Нортон из Кайзерслаутернского технического университета в Германии.

Теория представлений – это способ взять сложные объекты и «представить» их при помощи более простых. В роли сложных объектов часто выступают коллекции из математических объектов – числа или симметрии – находящиеся в определённых структурных отношениях друг с другом. Такие коллекции называют группами. Более простые объекты – это массивы чисел под названием матрицы, ключевой элемент линейной алгебры. Если группы – вещь абстрактная, и с ними часто тяжело работать, то матрицы и линейная алгебра – вещь элементарная.

«Математикам, по сути, про матрицы известно уже всё. Это одна из немногих математических тем, в которой мы хорошо и досконально разобрались», — сказал Джаред Вайнштайн из Бостонского университета.

Чтобы понять, как матрицы могут представлять группы, стоит рассматривать каждый объект по очереди.

Возьмём сначала группы. Чтобы упростить пример, возьмём шесть симметрий равностороннего треугольника:

Две вращательных (на 120° и 240°).
Три зеркальных (относительно линий, проведённых из каждой вершины через середину противоположной стороны).
Тождественная симметрия – когда с треугольником ничего не происходит.

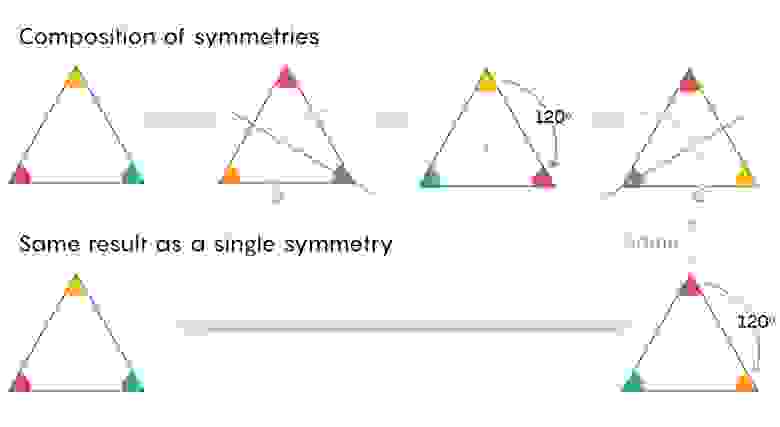
Шесть этих симметрий образуют замкнутую вселенную элементов – группу – формально именуемую S3. Это группа, поскольку любое количество этих симметрий можно применить к треугольнику последовательно и в любом порядке, а итоговый результат будет таким же, как если бы вы применили только одну. К примеру, если отразить треугольник, а потом повернуть его на 120°, то вершины переориентируются таким же образом, как если бы вы применили другое отражение.

«Делаю что-то одно, потом делаю что-то другое. Важно то, что в итоге получается всё равно симметрия треугольника», — сказал Нортон.

Математики называют комбинацию из двух симметрий композицией. Одно действие из группы (отражение) соединяется с другим (вращение) и даёт третье (другое отражение). Вслед за математиками композицию можно считать умножением.

«Нам нравится считать наши операции умножением, хотя это не перемножение чисел, а умножение преобразований», — сказал Нортон.

Это легко увидеть, если рассмотреть ненулевые вещественные числа, также формирующие группу. У вещественных чисел есть нейтральный элемент– число 1. Любое вещественное число, если его скомбинировать с 1, то есть, умножить на неё, остаётся неизменным. Также можно перемножать любую комбинацию вещественных чисел в любом порядке, и результат тоже всегда будет вещественным числом. Математики говорят, что группа вещественных чисел замкнута относительно умножения, то есть, из группы нельзя выйти, просто перемножая её элементы.

С момента открытия групп в 1830-х, они стали одним из наиболее важных объектов математики. Они кодируют информацию о простых числах, геометрических пространствах и вообще почти всего, что интересует математиков. Решение важной задачи часто превращается в изучение связанной с ней группы. Однако большинство групп гораздо сложнее понять, чем группу симметрий равностороннего треугольника. В группы Ли, к примеру, входит не шесть элементов, а бесконечное количество.

«Иногда группы становятся чересчур сложными», — сказал Вайнштейн.

И это подводит нас к теории представлений, превращающей загадочный периодами мир групп в хорошо известную нам территорию линейной алгебры.

Линейная алгебра изучает простейшие преобразования над объектами, известными, как векторы – по сути, направленными отрезками. Эти объекты определяются координатами, которые можно записать в виде матрицы – массива объектов.

Преобразование происходит при применении к вектору другой матрицы. К примеру, когда мы применяем к вектору матрицу

То он вытягивается в длину в два раза. Это пример линейного преобразования.

Другие матрицы выполняют другие линейные преобразования – отражения, повороты и сдвиги. Есть и нейтральная матрица, оставляющая вектор без изменений (точно так же, как тождественная симметрия оставляет треугольник неизменным, а число 1 оставляет неизменными другие числа).

Линейная алгебра определяет арифметику, стоящую за этими преобразованиями. Матрицы можно перемножать, складывать и вычитать так же легко, как мы проделываем это с числами.

Теория представлений создаёт мост между теорией групп и линейной алгеброй, назначая матрицу каждому элементу группы по определённым правилам. К примеру, нейтральному элементу группы нужно сопоставить нейтральную матрицу. Также эти назначения должны сохранять взаимоотношения элементов группы. Если отражение, умноженное на определённый поворот, равняется другому отражению, тогда матрица, сопоставленная первому отражению, умноженная на матрицу, сопоставленную повороту, должна равняться матрице, сопоставленной второму отражению. Набор матриц, удовлетворяющих этим требованиям, называется представлением группы.

Представление даёт упрощённую картину группы, так же, как чёрно-белая фотография может служить недорогой имитацией оригинального цветного изображения. Можно сказать, что оно «помнит» некоторую базовую, но необходимую информацию о группе, забывая всё остальное. Математики стремятся избегать необходимости иметь дело со всеми сложностями группы; вместо этого они получают представление о её свойствах, изучая то, как она ведёт себя при превращении в упрощённый формат линейных преобразований.

«Нам не нужно пытаться объятью всю группу сразу, — сказал Нортон. – Мы можем изучать её представление, меньшее по размеру, и всё равно что-то понять по поводу этой группы».

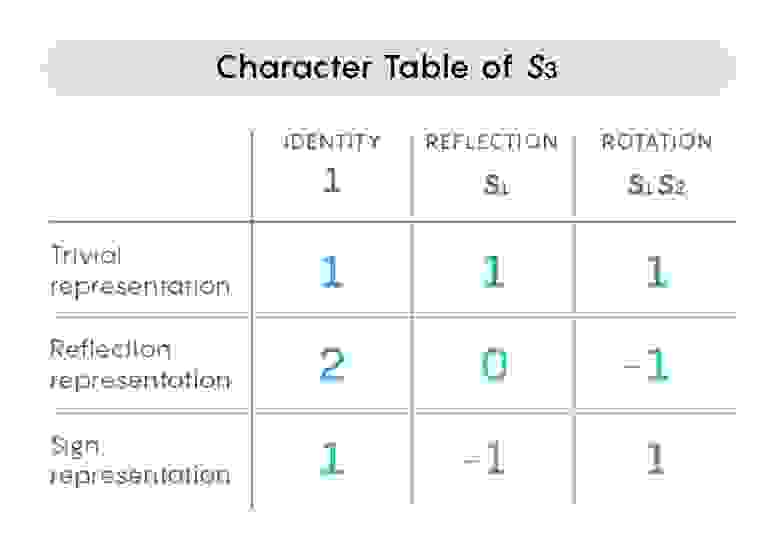
Почти всегда группу можно представить несколькими способами. К примеру, у S3 есть три разных представления через матрицы вещественных чисел: тривиальное, отражённое и знаковое.

Математики расставляют представления заданной группы в таблице — таблице характеров – где суммируется информация о группе. Строки обозначают каждое из различных представлений, а столбцы относятся к важным матрицам этих представлений – матрице, сопоставленной нейтральному элементу группы, и матрицам, сопоставленным «генерирующим» элементам, порождающим все остальные элементы. Элементами таблицы служат значения, которые называют «следами» матриц, и подсчитывают через сумму диагональных элементов от левого верхнего угла к правому нижнему. Ниже приводится таблица характеров для трёх представлений S3.

Таблица характеров даёт упрощённую картину группы. Каждое из входящих в неё представлений даёт свою, отличающуюся от других информацию. Математики комбинируют различные перспективы, которые дают им эти представления, и получают общее впечатление о группе.

«Много разных представлений помнят разные вещи, и если собрать всё это вместе, получится такая калейдоскопическая картинка вашей группы», — сказал Нортон.

В приведённой выше таблице характеров математики сразу же узнают таблицу для S3. Однако иногда одна и та же таблица характеров может представлять разные группы – при работе с упрощениями некая неоднозначность всегда возникает.

В таких неоднозначных случаях математики могут пользоваться дополнительными инструментами. Один из них – изменение числовой системы, в рамках которой они создают своё представление. Вышеуказанное представление S3 получается при помощи матриц с вещественными числами в качестве элементов – однако можно было бы использовать и комплексные числа (такие, у которых есть реальная и мнимая часть). Большая часть теории представлений их и использует.

Некоторые из самых продуктивных представлений не используют ни вещественные, ни комплексные числа. Они используют матрицы, элементы которых взяты из миниатюрных, или модульных числовых систем. Это мир «арифметики циферблата», в котором 7+6 оборачивается вокруг 12-часового циферблата и даёт 1. У двух групп с одинаковыми таблицами характеров в вещественном представлении могут быть разные таблицы характеров в модульном представлении, что позволяет различать их.

Сегодня теория представлений является основным инструментом для множества областей математики: алгебры, топологии, геометрии, математической физики и теории чисел – включая обширную программу Ленглендса.

«Философия теории представлений начала с огромной скоростью поглощать огромные области математики во второй половине XX века», — сказал мне Уильямсон.

Теория представлений – и в частности, модульные представления – сыграли важную роль в знаковом доказательстве Великой теоремы Ферма, полученном Эндрю Уайлсом в 1994 году. В задаче вставал вопрос о существовании решений уравнений вида a n + b n = c n в целых числах. Уайлс доказал, что для n>2 таких решений не существует. Если говорить примерно, то он доказывал, что если бы такие решения существовали, привели бы к появлению группы «эллиптической кривой» с весьма необычными свойствами. Эти свойства были настолько необычными, что казалось возможным доказать невозможность существования подобного объекта. Однако напрямую доказать, что он не существует, оказалось слишком тяжело. Вместо этого Уайлс обратился к семейству модульных представлений, которое было бы связано с этой группой, если бы она существовала. Он доказал, что такого семейства модульных представлений быть не может, что означает, что не может существовать и группы (или эллиптической кривой), что означает, что и решений тоже не существует.

Что, в свою очередь, означает, что примерно через 100 лет после того, как Уильям Бёрнсайд отбросил теорию представлений как бесполезную, она оказалась критически важным компонентом, возможно, наиболее знаменитого доказательства XX века.

«Я не мог придумать доказательства Великой теоремы Ферма, в котором бы нигде не использовалась теория представлений », — сказал Вайнштейн.

Видео:Правильные многоугольники. Геометрия 9 класс | Математика | TutorOnlineСкачать

Группы самосовмещений многоугольников и многогранников

По этой ссылке вы найдёте полный курс лекций по математике:

Сведения, излагаемые в этом параграфе, будут использованы при решении задач с помощью теории Пойа. Пусть F — геометрическая фигура. Под самосовмещением фигуры F понимают такое перемещение (движение) F (в пространстве или на плоскости), которое переводит F в F. Тривиальным примером самосовмещения является тождественное преобразование с, при котором каждая точка переходит сама в себя. Рассмотрим множество G всех самосовмещен ий фигуры F.

Произведение дх -д2 двух самосовмещений д и дг определим как композицию движений pite) — это движение, возникающее в результате последовательного выполнения а затем д]. Легко проверить, что — группа. Чем «более симметричной» будет фигура F, тем «более богатой» будет ее группа самосовмещений. Например, для круга и шара соответствующие группы бесконечны. Группы самосовмещений многоугольников и многогранников Группа вращений правильного n-угольника.

Под вращением правильного п-уголь-ника будем понимать поворот в его плоскости, приводящий к его самосовмещению. Очевидно, что если поворот нетривиален (т.е. не является тождественным преобразованием), то его центром является центр правильного n-угольника. Поскольку при вращении всякая вершина должна перейти в вершину, угол поворота (с точностью до угла, кратного 2тт) равен кк = 0,1. п — 1. Группа снмметрнй правильного п-угольника.

Под симметрией правильного п-уголь-ника будем понимать его самосовмещение в пространстве. К перечисленным выше поворотам в плоскости добавляются «опрокидывания* многоугольника, т.е. повороты на 180° вокруг осей симметрии многоугольника8^. Их ровно п штук. Если п четно, то осями симметрии являются п/2 прямых, соед»жяющих пары противоположных вершин многоугольника, и п/2 прямых, соединяющих середины его противоположных сторон.

При нечетном п каждая из осей симметрии проходит через некоторую вершину n-угольника и середину противоположной стороны. Группы вращений многогранников. Под вращением многогранника будем понимать его самосовмещение. 1. Куб. Сначала покажем, что группа вращений куба содержит 24 элемента. Будем считать, что куб расположен таким образом, что о его гранях можно говорить: нижняя, верхняя, передняя и т.д.

Самосовмещение куба полностью определяется тем, 1) какая грань из шести станет нижней и 2) какая из смежных с ней граней будет передней. Согласно правилу произведения имеется всего 6 • 4 = 24 разных самосовмещения. Перечислим их: • тождественное преобразование; Группы самосовмещений многоугольников и многогранников • повороты на ±90 180° вокруг прямых, соединяющих центры противоположных граней (таких вращений 3-3 = 9);

Эти преобразования равносильны осевым симмстриям. • повороты на 180° вокруг прямых, соединяющих середины противоположных ребер куба (6); • повороты на ±120° вокруг диагоналей куба (8)9 Легко проверить (рассмотрев, например, подстановки на множестве вершин, порождаемые вращениями), что все эти самосовмещения различны; так как всего их ровно 24, других самосовмещений нет. 2. Тетраэдр. Под тетраэдром будем понимать правильный тетраэдр.

Возможно вам будут полезны данные страницы:

Будем считать, что тетраэдр расположен в пространстве таким образом, что о его гранях можно говорить: нижняя, передняя, задние левая и правая. Самосовмещение тетраэдра полностью определяется тем, 1) какая грань из четырех становится нижней и 2) какая из оставшихся трех граней будет передней. Таким образом, всего данная группа содержит 4 • 3 = 12 элементов: • тождественное преобразование; • повороты на ±120° вокруг высот тетраэдра (всего 8 таких поворотов); • повороты на 180° вокруг прямых, соединяющих середины скрещивающихся ребер тетраэдра (таких поворотов 3).

Все названные самосовмешения различны, общее их число 12; поэтому они исчерпывают рассматриваемую группу.

3. Правильная n-угольная пирамида. Очевидно, что группа вращений правильной n-угольной пирамиды, отличной от правильного тетраэдра, изоморфна группе вращений правильного n-угольника, лежащего в ее основании. 4. Двойная пирамида (диэдр). Эта геометрическая фигура представляет собой объединение двух одинаковых правильных п-угольных пирамид, чьи основания совмещены, а вершины находятся по разные стороны от основания.

Если диэдр не является октаэдром, то его группа вращений изоморфна группе симметрий правильного п-угольника. Как известно, октаэдр — многогранник, двойственный кубу (центры граней октаэдра являются вершинами некоторого куба; центры граней куба являются вершинами некоторого октаэдра). Неудивительно поэтому, что группы вращений октаэдра и куба изоморфны. То же справедливо и для групп вращений двух оставшихся правильных многогранников10). 5.

Икосаэдр и додекаэдр. Рассуждая так же, как и в случае куба или тетраэдра, легко найти число элементов группы самосовмешений додекаэдра, зная, что он имеет 20 вершин и из каждой вершины исходит 3 ребра. 9) Рассмотрим, например, поворот куба ABCDABCD вокруг диагонали АС. Высота треугольной пирамиды ABDA лежит на диагонали АС; основанием этой пирамиды яа!яется правильный треугольник В А D (каждая его сторона — диагональ грани куба), который самосовмсшастся при поворотах на углы, кратные 120°. |0) Всего правильных многогранников — ровно пять: тетраэдр, куб, октаэдр, икосаэдр, додекаэдр. Упражнения 1.

Какими свойствами (рефлексивность, антирефлексивность,

симметричносгь, антисимметричность, транзитивность) обладают следующие бинарные отношения на множестве действительных чисел? 2. Какие из отношений предыдущей задачи являются отношениями эквивалентности? Для каждого из таких отношений выяснить, что представляют собой классы эквивалентности и сколько элементов они содержат.

3. На множестве учеников класса введем отношение «учится лучше». Будем говорить «Ученик А учится лучше ученика В», если по большинству контрольных работ А имел оценки выше, чем В. Обладает ли данное отношение свойством транзитивности? 4. На множестве А введено симметричное и транзитивное отношение К такое, что Доказать, что отношение Я рефлексивно. Соглашение. В задачах данного раздела е обозначает нейтральный элемент группы.

Пусть конечное множество, на котором определена бинарная операция Таблица из п строк и п столбцов, в которой на пересечении i-й строим и j-ro столбца стоит элемент множества А, равный а, * о^, называется таблицей умножения, или квадратом Кэаи. 5. На множестве > определим две бинарные операции: Группы самосовмещений многоугольников и многогранников 1) (наибольший общий делитель); 2) (наименьшее о§щее кратное). Составить для этих операций квадраты Кэли. 6.

Составим матрицу коэффициентов дробно-линейной функции Какая матрица будет соответствовать сложной функции На множестве функций выберем в качестве бинарной операции композицию функций (будем считать, что областью определения всех функций является множество R). Составить квадрат Кэли для данной операции.

Доказать, что рассматриваемая алгебраическая структура является группой. 8. На множестве (Q 0) х Q введена операция Доказать, что данная алгебраическая структура является группой. 9. Доказать, что в квадрате Кэли конечной группы каждый элемент группы встречается в каждой строке (и каждом столбце) ровно один раз. 10. Составить квадрат Кэли для следующих групп: 1) вращений правильного треугольника; 2) вращений квадрата; 3) вращений правильного пятиугольника;

4) симметрий ромба, не являющегося квадратом; 5) симметрий правильного треугольника; 6) симметрии прямоугольника, не являющегося квадратом; 7) симметрий квадрата. 11. Доказать, что группа из задачи 7 изоморфна группе симметрии квадрата. 12. Какие из следующих числовых множеств образуют аддитивные группы? 3.

Какие из следующих числовых множеств образуют мультипликативные группы? 14. Доказать, что если в группе каждый элемент себе обратен , то группа — абелева. 15. Найти с точностью до изоморфизма все группы, состоящие не более чем из 4 элементов. 16. Пусть — сюръективное гомоморфное отображение абелевой группы G на группу Н. Доказать, что Я — абелева группа. 17. Пусть ( — группа, д 6 G. Доказать, что отображение , заданное правилом , является изоморфизмом. 1В.

Пусть — конечная группа. Доказать, что Наменьшее п > 0, при котором дя = е, называют порядком элемента д. 19. Порядком конечной группы называется количество ее членов. Доказать, что конечная группа четного порядка обязательно содержит элемент второго порядка. 20. Пусть группа обладает единственным элементом второго порядка. Доказать, что этот элемент перестановочен с каждым элементом группы. Ответы 1. См. табл. Нет. 5. НОД (табл. 4). НОК (табл. 5). См. табл. 6.

8. Указание. Нейтрааьный элемент , обратный 9. Возьмем строку, соответствующую элементу а. В ней встретится элемент Ь, если для некоторого элемента х выполняется равенство . Аналогично, в столбце, соответствующем элемент>’ о. встретится элемент b, если для некоторого элемента у выполняется равенство Таким образом, задача сводится к доказательству существования и единственности решения каждого из уравнений (1) и (2).

Умножив равенство (1) слева на элемент а’ (элемент, обратный к а), получим х — а’ *Ь. Значит, если решение уравнения (1) существует, то оно единственно. С другой стороны, непосредственной подстановкой в (1) убеждаемся, что а’ *Ь — решение. Аналогично, находим решение уравнения 15. Указание. Использовать результат упражнения 9. Приведем набросок решения для случая п = 4. Один из элементов гру ппы — нейтральный (е); пусть три других — a, b и с.

Рассмотрим два возможных случая. 1. Каждый элемент группы себе обратен . каждый элемент диагонали квадрата Кэли — е. Ясно, как выглядят строка и столбец, отвечающие е. Теперь нам предстоит заполнить пустые клетки в таблице На пересечении второй строки и третьего столбца может стоять только элемент с, так как во второй строке уже есть элементы а и е, а в третьем столбце — элемент b (напомним, что в каждой строке и каждом столбце квадрата Кэли по одному разу встречается каждый элемент группы). Аналогичные рассуждения позволяют однозначно заполнить оставшиеся клетки таблицы.

Операция, заданная полученной таблицей, удовлетворяет аксиомам (Gl), (G3) и (G4). Осталось проверить выполнение аксиомы (G2). Это можно сделать непосредственно либо привести пример группы, имеющей данный квадрат Кэли. 2. Не каждый элемент группы себе обратен. Пусть, например, а2 = Ь. Имеем таблицу Хотя в ней пустых клеток больше, чем в предьиушем случае, но и она заполняется однозначно. Здесь удобно начать с пересечения второй строки и четвертого столбца.

16. Указание. Воспользоваться тем, что у каждого элемента группы Я есть прообраз в G и тем, что в силу коммутативности G. 17. Указание. Заметить, Группы самосовмещений многоугольников и многогранников 18. Указание. В силу конечности группы в последовательности степеней есть одинаковые элементы. 19. Если а’ — элемент, обратный к а, то о — элемент, обратный к о’. Стало быть, элементы порядка выше второго (для каждого такого элемента а имеем а Ф а) разбиваются на пары взаимно обратных.

Поэтому в группе (с четным числом элементов) содержится и четное число элементов порядка 1 и 2. Но порядок 1 имеет только нейтральный элемент. Значит, порядок 2 имеют нечетное число элементов. 20. Пусть — произвольный элемент группы. Докажите, что ада

Присылайте задания в любое время дня и ночи в ➔

Официальный сайт Брильёновой Натальи Валерьевны преподавателя кафедры информатики и электроники Екатеринбургского государственного института.

Все авторские права на размещённые материалы сохранены за правообладателями этих материалов. Любое коммерческое и/или иное использование кроме предварительного ознакомления материалов сайта natalibrilenova.ru запрещено. Публикация и распространение размещённых материалов не преследует за собой коммерческой и/или любой другой выгоды.

Сайт предназначен для облегчения образовательного путешествия студентам очникам и заочникам по вопросам обучения . Наталья Брильёнова не предлагает и не оказывает товары и услуги.

Видео:Группы симметрий правильных многогранниковСкачать

Теория конечных групп симметрий

алгебраический математика симметрия число

Группа симметрии (также группа симметрий) некоторого объекта (многогранника или множества точек из метрического пространства) Ї это группа всех движений, для которых данный объект является инвариантом, с композицией в качестве групповой операции. Как правило, рассматриваются множества точек n-мерного евклидова пространства и движения этого пространства, но понятие группы симметрии сохраняет свой смысл и в более общих случаях.

Группа симметрии равностороннего треугольника на плоскости состоит из тождественного преобразования, поворотов на углы 120° и 240° вокруг центра треугольника и отражений относительно его высот. В этом случае группа симметрии состоит из 6 преобразований, которые осуществляют все возможные перестановки вершин треугольника. Следовательно, эта группа изоморфна симметрической группе S3. Однако группа симметрии квадрата имеет порядок 8, а симметрическая группа S4 изоморфна группе симметрии правильного тетраэдра.

Группа симметрии разностороннего треугольника тривиальна, то есть состоит из одного элемента Ї тождественного преобразования.

Если считать, что человеческое тело зеркально симметрично, то его группа симметрии состоит двух элементов: тождественного преобразования и отражения относительно плоскости, которая делит тело на симметричные друг другу правую и левую части.

Произвольное периодическое замощение плоскости (или орнамент) имеет группу симметрии, элементы которой всеми возможными способами совмещают некий фиксированный элемент замощения с каждым конгруэнтным ему элементом.