Свойство серединного перпендикуляра треугольника

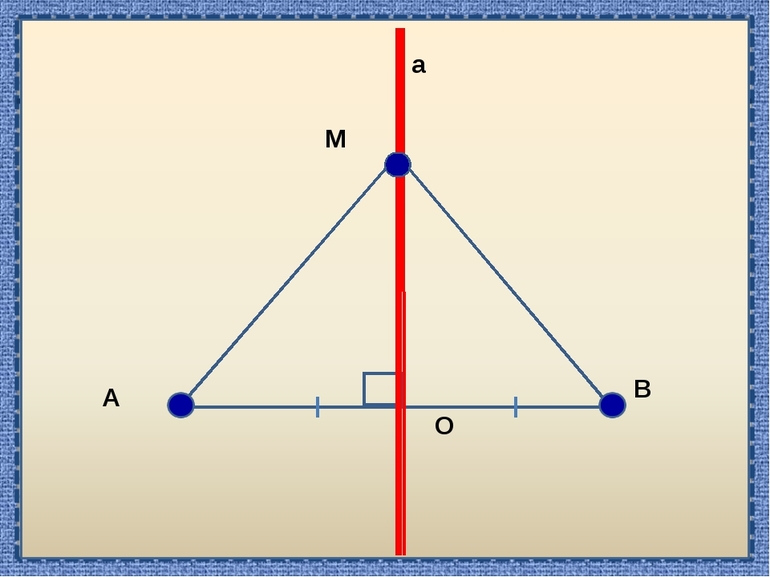
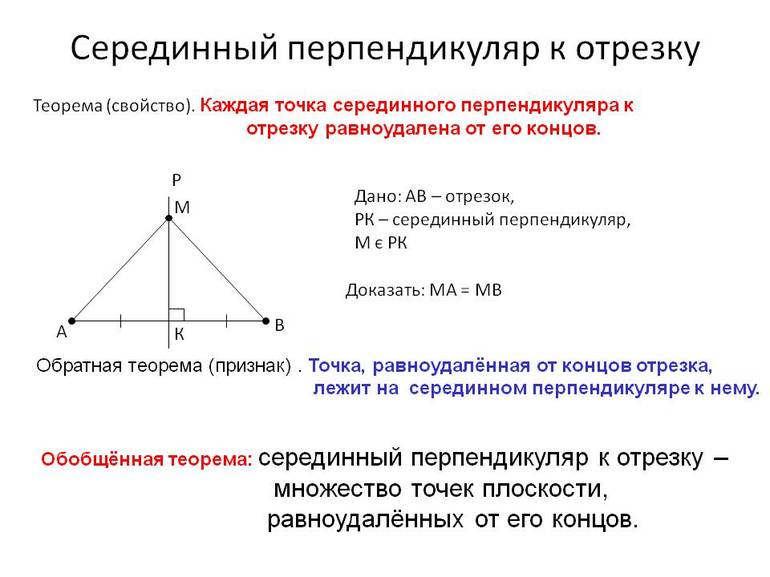
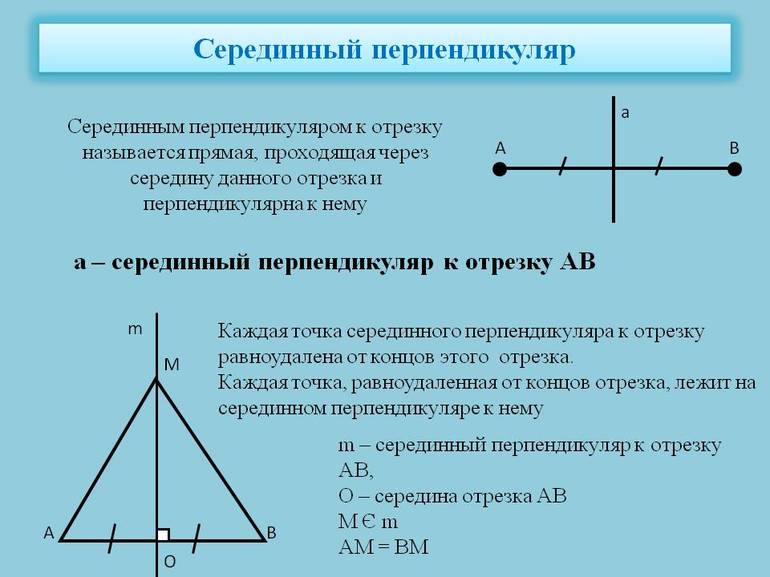
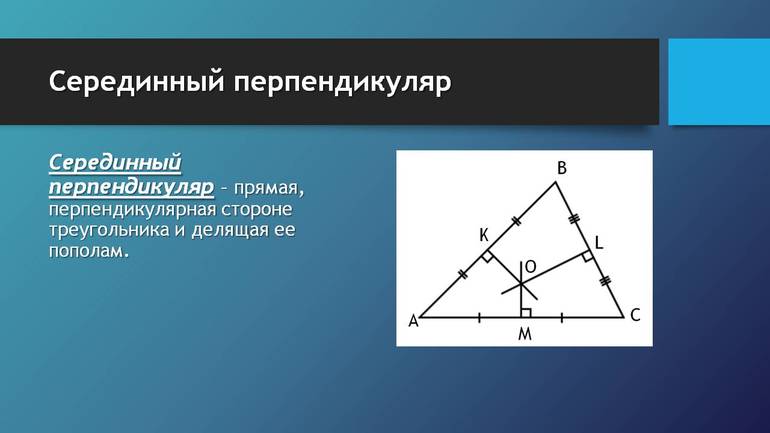
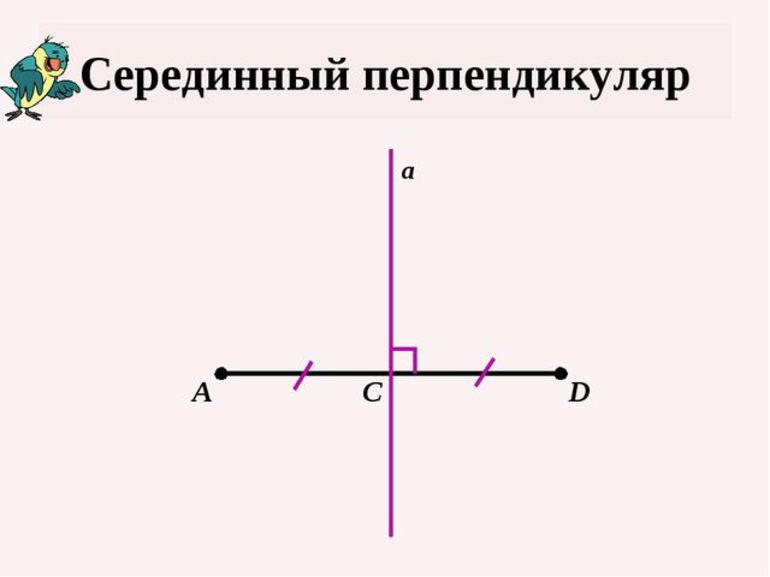
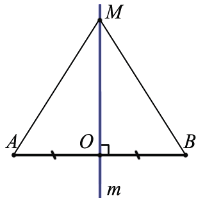
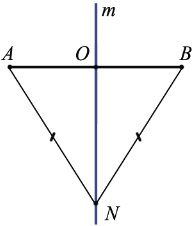
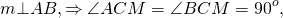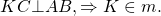Рассмотрим свойства серединного перпендикуляра. Начнем со свойства серединного перпендикуляра к отрезку.

I) Каждая точка серединного перпендикуляра к отрезку равноудалена от концов этого отрезка.

II) И обратно: каждая точка, равноудаленная от концов отрезка, лежит на серединном перпендикуляре к нему.

I)

AB- отрезок, C — середина AB,

m — серединный перпендикуляр к AB,

1. Если точка M совпадает с точкой C.

Так как AC=BC по условию, то и AM=BM.

2. Если точка M не совпадает с точкой C.

Рассмотрим треугольники ACM и BCM

то есть треугольники ACM и BCM — прямоугольные.

AC=BC (по условию), CM — общий катет.

Из равенства треугольников следует равенство соответствующих сторон: AM=BM.

Что и требовалось доказать.

II) Дано: AB — отрезок, C — середина AB,

m — серединный перпендикуляр к AB,

Так как AK=BK (по условию), то треугольник AKB — равнобедренный с основанием AB (по определению). Так как C — середина AB, то KC — медиана треугольника AKB.

По свойству равнобедренного треугольника медиана, проведенная к основанию, является также его высотой, то есть

Что и требовалось доказать.

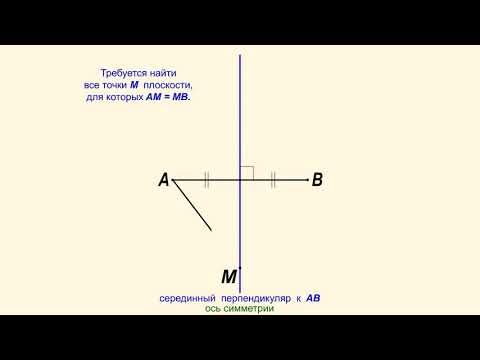
Геометрическое место точек, равноудаленных от двух данных точек, есть серединный перпендикуляр к отрезку, соединяющему эти точки.

В следующий раз рассмотрим свойство серединных перпендикуляров к сторонам треугольника.

Видео:Геометрия 8 класс (Урок№30 - Свойство серединного перпендикуляра.)Скачать

Серединный перпендикуляр — определение, свойства и формулы

Видео:Свойство точек серединного перпендикуляра (серпера)Скачать

Общие сведения

Серединным перпендикуляром отрезка называют прямую, которая проходит под прямым углом через среднюю точку, т. е. середину отрезка. Для полного понимания материала следует остановиться на базовых элементах геометрии.

Точка — единица, при помощи которой строятся прямые, отрезки, лучи и фигуры. Прямая — простая фигура в форме бесконечной линии, состоящей из множества точек, лежащих в одной плоскости. Луч — базовая геометрическая фигура в виде бесконечной линии с одной стороны и точки-ограничителя — с другой. Иными словами, луч имеет начало, но не имеет конца. Отрезок — некоторая часть прямой (луча или другого отрезка), ограниченная двумя точками.

Кроме того, в геометрии серединный перпендикуляр встречается в треугольниках. Из определения можно сделать вывод, что им может быть прямая, отрезок и даже луч.

Аксиомы геометрии Евклида

Евклидовой геометрией называется наука о фигурах на плоскости, основанная на аксиомах и теоремах. Аксиома — базовое утверждение, не требующее доказательства. Оно используется для доказательства каких-либо теорем. Математики выделяют пять аксиом:

1. Принадлежности.
2. Порядка.
3. Конгруэнтности.
4. Параллельности прямых.
5. Непрерывности.

Формулировка первой имеет такой вид: если существует в геометрическом пространстве плоскость, состоящая из множества точек, то через любые из них можно провести только одну прямую. Иными словами, можно взять произвольные две точки и провести через них одну прямую. Чтобы начертить еще одну прямую, следует взять две другие точки.

Следующее утверждение называется аксиомой порядка. Она гласит, что существует точка, которая лежит между двумя другими на прямой. Значение слова «конгруэнтность» не совсем понятно для новичка, однако нужно постепенно привыкать к терминологии. Оно обозначает «равенство». Третий геометрический факт формулируется таким образом: когда два отрезка или угла конгруэнтны третьему, тогда они равны между собой. Аксиома касается только отрезков и углов.

Чтобы убедиться в ее правильности, нужно разобрать следующий пример: длина первого отрезка составляет 10 см, второго — тоже, а третий равен первому. Необходимо доказать, что они равны между собой. Это делается очень просто:

• Вводятся обозначения: первый — MN, второй — OP и третий — RS.
• Устанавливаются значения по условию: MN = 10 см, ОР = 10 см, а RS = MN.
• Доказательство строится таким образом: MN = RS = 10 (см). Следовательно, отрезки равны, поскольку MN = ОР = RS = 10 (см).

Следует отметить, что данные действия оказались лишними — было потрачено время на понимание простой «истины». Параллельность прямых является также аксиомой и формулируется таким образом: если существует некоторая прямая на плоскости и точка, не лежащая на ней, то через последнюю можно провести только одну параллельную ей прямую.

И последняя аксиома называется Архимедовой. Ее формулировка имеет такой вид: для произвольных отрезков, лежащих на одной прямой, существует некоторая последовательность базовых элементов (точек), лежащих на одном и другом отрезках, таких, что заданные их части равны между собой. Иными словами, на одной прямой могут быть расположены равные между собой отрезки.

Информация о треугольниках

Треугольником является любая фигура, состоящая из трех вершин (точек) соединенных отрезками (сторонами), причем точки не лежат на одной прямой в одной плоскости. Они классифицируются по такому типу:

В первом случае фигуры делятся на остроугольные, тупоугольные и прямоугольные. Остроугольным называется треугольник, у которого все углы острые (меньше 90 градусов). У тупоугольного — один угол тупой (> 90), а в прямоугольном — один из углов равен 90 градусам. Следует отметить, что сумма градусных мер углов любого треугольника эквивалентна 180.

Когда стороны у треугольника неравны между собой, тогда его называют разносторонним. При равенстве двух боковых сторон он считается равнобедренным, у которого третья сторона — основание. Если все стороны равны, то значит, фигура является равносторонней или правильной.

У треугольника есть еще и другие параметры. Их называют медианой, биссектрисой и высотой. Первый параметр является отрезком, который проводится из любой вершины на среднюю точку стороны. Высота — часть прямой, которая проводится из произвольной вершины и перпендикулярна противоположной стороне. Биссектрисой называется прямая, делящая угол на две равные части.

Медиана, высота и биссектриса, проведенные из вершины к основанию, совпадают и эквивалентны серединному перпендикуляру в треугольниках равнобедренного и равностороннего типов. Это очень важно при решении задач. Еще одним признаком, по которому выполняется классификация — подобность треугольников. У них могут быть равными только углы и некоторые стороны. Они отличаются между собой по определенному параметру, который называется коэффициентом подобия. Последний влияет только на размерность сторон. Говорят, что фигуры подобны по определенному признаку (их всего три).

Видео:8 класс, 36 урок, Свойства серединного перпендикуляра к отрезкуСкачать

Основные теоремы

Теорема — гипотеза (предположение), которую нужно доказать. Они применяются для оптимизации расчетов и вычисления отдельных параметров заданной фигуры. Кроме того, существуют следствия, полученные при доказательстве таких научных предположений. Эти аспекты упрощают и автоматизируют вычисления. Например, при вычислении площади треугольника нет необходимости выводить формулу, достаточно воспользоваться уже готовой.

Математики выделяют всего три теоремы о СП, которые могут значительно упростить расчеты. К ним можно отнести следующие:

• Прямая.
• Обратная.
• Пересечение в треугольнике.

Первая теорема называется прямой о СП. Она показывает, каким свойством обладают точки серединного перпендикуляра. Ее формулировка следующая: произвольная точка, которая взятая на перпендикуляре, удалена на равные расстояния от конечных точек отрезка, ограничивающих его на плоскости.

Для доказательства следует рассмотреть два прямоугольных треугольника с общей вершиной (искомая точка), общей стороной — катетом и равными катетами (по определению). Фигуры равны по одному из признаков равенства треугольников. Следовательно, их гипотенузы (стороны, равенство которых нужно доказать), равны между собой. Первая теорема доказана.

Следующая теорема — обратная: если точка удалена на равные расстояния от концов отрезка, то значит, она лежит на СП. В этом случае следует рассматривать равнобедренный треугольник, вершиной которого она является. Удалена точка на одинаковые расстояния от вершин основания по условию. Следовательно, этот факт доказывает, что полученный треугольник является равнобедренным, а в нем медиана, проведенная к основанию, является биссектрисой и высотой. Значит, она лежит на серединном перпендикуляре. Утверждение доказано.

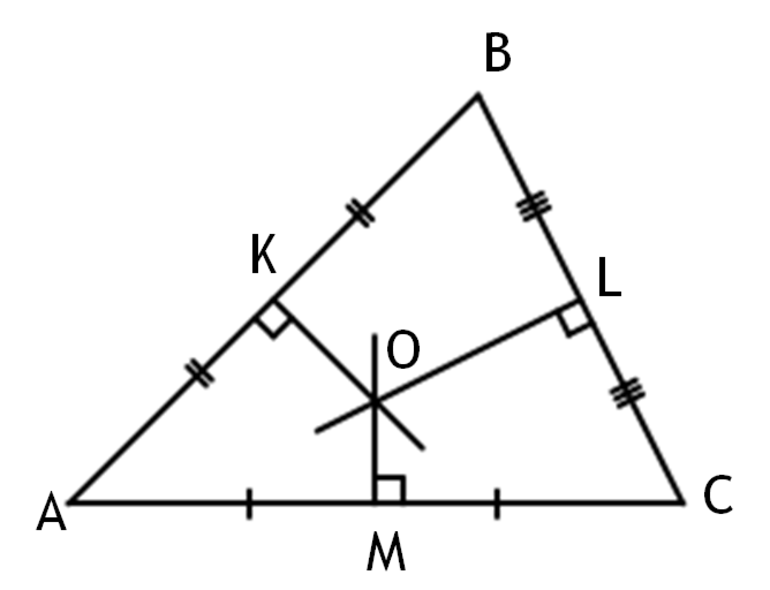
Следующую теорему нет необходимости доказывать, поскольку известно, что в равнобедренном и равностороннем треугольниках высоты (медианы и биссектрисы) имеют общую точку пересечения. Они являются также и СП. Следовательно, это утверждение справедливо для них.

Видео:Свойства и признаки равнобедренного треугольника Серединный перпендикулярСкачать

Важные свойства

Иногда трех теорем недостаточно для решения какой-либо сложной задачи. В этом случае необходимо знать еще и некоторые свойства СП:

1. Центр описанной окружности вокруг треугольника соответствует точке их пересечения.
2. Точка, взятая на СП, равноудалена от конечных точек отрезка и образует равнобедренный или равносторонний треугольник.
3. В треугольниках равнобедренного и равностороннего типов им является высота, медиана и биссектриса.

В первом случае все зависит от типа треугольника. Если он является остроугольным, то центр лежит внутри него. Для тупоугольного — во внешнем пространстве, а в прямоугольном — на середине гипотенузы.

Следует отметить, что есть формулы для его расчета. Если предположить, что существует некоторый произвольный треугольник со сторонами а, b и с. Кроме того, для них выполняется условие a >= b >= c. Исходя из полученных данных, можно записать формулы перпендикуляров (Р), проведенных к определенной стороне:

1. а: Pa = (2 * а * S) / (a^2 + b^2 — c^2).
2. b: Pb = (2 * b * S) / (a^2 + b^2 — c^2).
3. c: Pc = (2 * c * S) / (a^2 — b^2 + c^2).

Иными словами, Р является отношением удвоенного произведения стороны на площадь треугольника к сумме квадратов смежных сторон без квадрата противоположной. Кроме того, справедливы неравенства: Pa >= Pb и Pс >= Pb. Стороны — известные параметры, а вот площадь находится по некоторым соотношениям, которые выглядят следующим образом:

1. Основание и высоту, проведенную к нему: S = (1/2) * a * Ha = (1/2) * b * Hb = (1/2) * c * Hc.
2. Через радиус вписанной окружности: S = (1/2) * r * (a + b + c).
3. Формулу Герона через полупериметр (р) и без него: S = [p * (p — a) * (p — b) * (p — c)]^(1/2) и S = 1/4 * [(a + b + c) * (b + c — a) * (а + c — b) * (a + b — c)]^(1/2).

В основном по таким соотношениям и нужно определить площадь. Полупериметр вычисляется таким образом: р = (а + b + с) / 2.

Бывают задачи, в которых необходимо просто подставить значения в формулу. Они называются простейшими. Однако встречаются и сложные. К ним относятся все виды без некоторых промежуточных параметров фигуры.

Видео:Свойство серединного перпендикуляраСкачать

Пример решения задачи

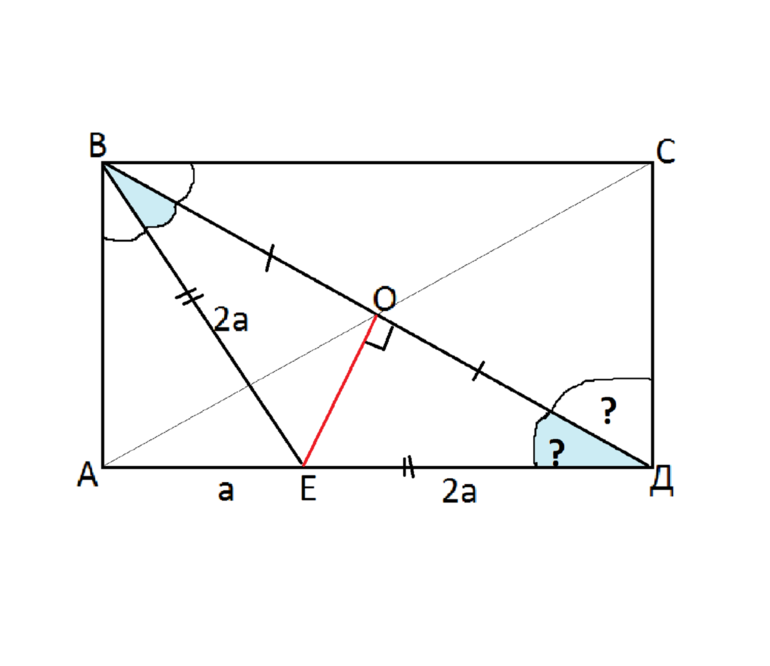
В интернете попадаются примеры решения простых задач, а сложные приходится решать самостоятельно, просить помощи у кого-нибудь или покупать на сайтах готовое решение. Для примера нужно решить задание с такими данными:

1. Прямоугольник, изображенный на рисунке 1 с диагональю равной d.
2. Серединный перпендикуляр, проведенный к диагонали прямоугольника.
3. Точка Е делит сторону на отрезки а и 2а.

Нужно найти: углы, указанные на рисунке, стороны и ОЕ. Кроме того, дополнительные данные можно узнать из чертежа, который используется для решения задачи (рис. 1). К любому заданию нужно делать графическое представление, поскольку оно позволяет избежать ошибок при вычислении

Рисунок 1. Чертеж для решения задачи.

Числовых значений нет, тогда необходимо решать в общем виде. Углы можно найти по такому алгоритму:

1. Нужно рассмотреть треугольник ВДЕ. Он является равнобедренным, поскольку ОЕ — СП, а диагональ — отрезок. Следовательно, ВЕ = ДЕ = 2а.
2. Необходимо найти угол ЕВО. Сделать это проблемно. Рекомендуется обратить внимание на треугольник АВЕ.
3. При помощи тригонометрической функции синуса можно вычислить значение угла АBE: sin(АBE) = a/2а = 0,5. Следовательно, arcsin(0,5) = 30 (градусов).
4. Угол СВЕ вычисляется следующим образом: 90 — 30 = 60 (градусов).
5. Следовательно, искомый угол равен 30, поскольку 90 — 30 — 30 = 30.
6. В равнобедренном треугольнике углы при основании равны между собой: ЕДО = ЕВО = 30 (градусов).

Для нахождения сторон нужно составить уравнение в общем виде, обозначив неизвестную величину АВ литерой «х». Рассмотрев прямоугольный треугольник АВЕ, по теореме Пифагора можно вычислить АВ: x = [4a^2 + a^2]^(1/2) = a * [5]^(1/2). Следовательно, АВ = a * [5]^(1/2) и ВС = 3а. ОЕ находится по формуле: ОЕ = (2 * 2 * а * S) / (8 * a^2 — d^2). Можно править соотношение таким образом через прямоугольный треугольник ДОЕ: ОЕ = [4 * a^2 — (d^2) / 4]^(1/2).

Таким образом, нахождение серединного перпендикуляра позволяет значительно уменьшить объемы вычислений. Однако для этого нужно знать не только основные теоремы, но и его свойства.

Видео:75. Свойства серединного перпендикуляра к отрезкуСкачать

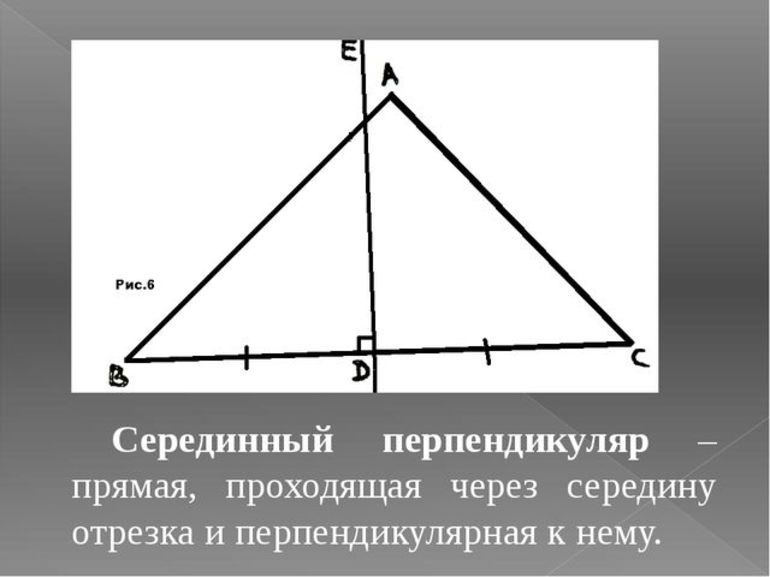
Свойства серединного перпендикуляра к отрезку

Серединным перпендикуляром к отрезку называется прямая, проходящая через середину данного отрезка и перпендикулярная к нему.

— серединный перпендикуляр к отрезку АВ.

Теорема

Каждая точка серединного перпендикуляра к отрезку равноудалена от концов этого отрезка.

Обратно: каждая точка, равноудалённая от концов отрезка, лежит на серединном перпендикуляре к нему.

Доказательство

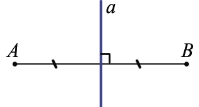
1) Дано: m — серединный перпендикуляр отрезка АВ, О — середина АВ, Мm

Доказать: АМ = ВМ

Доказательство:

Если О = М, то АМ = ВМ, т.к. О — середина АВ.

Пусть О 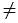М. Рассмотрим ОАМ и ОВМ: так как m — серединный перпендикуляр отрезка АВ, то рассматриваемые треугольники прямоугольные. ОА = ОВ, т.к. О — середина отрезка АВ, ОМ — общий катет, следовательно, ОАМ = ОВМ, по двум катетам, а в равных треугольниках против соответственно равных углов лежат равные стороны, поэтому АМ = ВМ.

2) Дано: m — серединный перпендикуляр отрезка АВ, О — середина АВ, АN = ВN

Доказать: N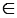m

Доказательство:

Рассмотрим произвольную точку N.

Если N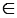АВ, то N = О, а, значит, она лежит на прямой m.

Если N не лежит на АВ, то ANB — равнобедренный, так как АN = ВN. О — середина АВ, следовательно, NО — медиана ANB, а, значит, и высота по свойству равнобедренного треугольника. Поэтому NОАВ, следовательно, прямые NО и m совпадают, так как по устовию m — серединный перпендикуляр отрезка АВ, т.е. N — точка прямой m. Теорема доказана.

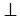
Следствие 1

Следствие2

Поделись с друзьями в социальных сетях:

🔥 Видео

Урок 30 свойство серединного перпендикуляра Геометрия 8Скачать

Свойство серединного перпендикуляра к отрезкуСкачать

Урок 12. Серединный перпендикуляр к отрезку (7 класс)Скачать

Серединный перпендикуляр к стороне треугольника. Построение.Скачать

Серединный перпендикулярСкачать

32 Свойство серединного перпендикуляра к отрезкуСкачать

Св-ва биссектрисы угла и серединного перпендикуляра к отрезку | Геометрия 7-9 класс #72 | ИнфоурокСкачать

ГЕОМЕТРИЯ УРОК 7 // СВОЙСТВО БИССЕКТРИСЫ И СЕРЕДИННОГО ПЕРПЕНДИКУЛЯРА // НАТАЛЬЯ СААКЯНСкачать

Замечательные точки треугольника | Ботай со мной #030 | Борис Трушин ||Скачать

Построение серединных перпендикуляров треугольника с помощью подручных средствСкачать

Свойство серединного перпенд ТеорияСкачать

Свойство биссектрисы. Понятие и свойство серединного перпендикуляра к отрезку.Скачать

Построение серединных перпендикуляров треугольника с помощью циркуляСкачать

Серединный перпендикуляр. 7 класс геометрия. Центр описанной окружности треугольникаСкачать