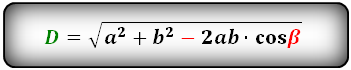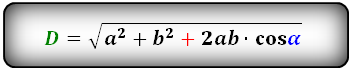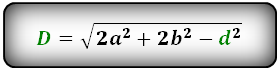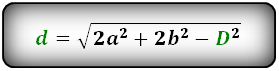В данной публикации мы рассмотрим, каким образом можно посчитать периметр параллелограмма и разберем примеры решения задач.
- Формула вычисления периметра
- Примеры задач
- Как найти периметр параллелограмма через диагонали
- Признаки параллелограмма
- Основные свойства параллелограмма
- Стороны параллелограмма
- Формулы определения длин сторон параллелограмма:
- Диагонали параллелограмма
- Формулы определения длины диагонали параллелограмма:
- Периметр параллелограмма
- Формулы определения длины периметра параллелограмма:
- Площадь параллелограмма
- Формулы определения площади параллелограмма:
- Как найти периметр квадрата, прямоугольника, параллелограмма, трапеции, ромба, эллипса, многоугольника
- Периметр квадрата
- Периметр прямоугольника
- Готовые работы на аналогичную тему
- Периметр параллелограмма
- Периметр трапеции
- Периметр ромба
- Периметр многоугольника
- Периметр эллипса
- 📽️ Видео
Видео:№375. Найдите периметр параллелограмма, если биссектриса одного из его углов делитСкачать
Формула вычисления периметра
Периметр (P) параллелограмма равняется сумме длин всех его сторон. А т.к. противоположные стороны данной фигуры равны, формулу можно представить в следующем виде:
P = 2 * (a + b) или P = 2a + 2b
Видео:Периметр треугольника. Как найти периметр треугольника?Скачать

Примеры задач
Задание 1
Найдите периметр параллелограмма, если его стороны равны 6 и 8 см.
Решение:
Воспользуемся одной из двух формул выше, подставив в нее известные значения: P = 2 * 6 см + 2 * 8 см = 28 см.
Тот же самый результат получится, если применить вторую формулу: P = 2 * (6 см + 8 см) = 28 см.
Задание 2
Периметр параллелограмма равен 50 см. Найдите его вторую сторону, если известно, что первая равна 7 см.
Решение:
Нам известно, что периметр считается по формуле: P = 2a + 2b.
Допустим a – это известная сторона, и нам нужно найти b. Ее длина, умноженная на два, равна: 2b = P – 2a = 50 см – 2 * 7 см = 36 см.
Следовательно, длина неизвестной стороны составляет: b = 36 см / 2 = 18 см.
Видео:Все про ПАРАЛЛЕЛОГРАММ за 8 минут: Свойства, Признаки, Формулы Периметра и Площади // ГеометрияСкачать

Как найти периметр параллелограмма через диагонали
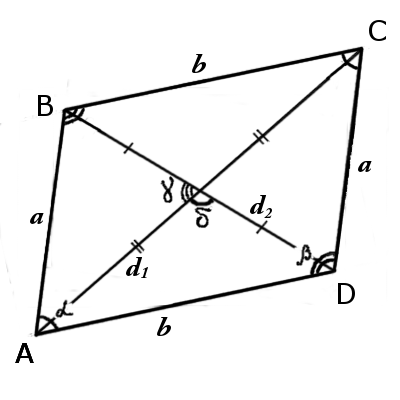 | 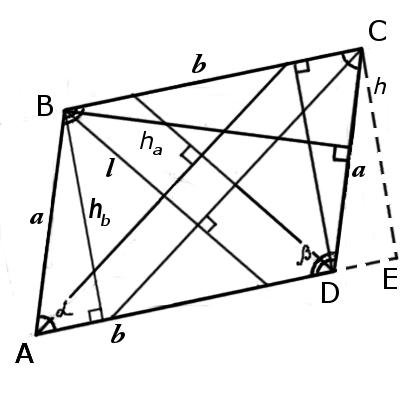 |
| Рис.1 | Рис.2 |
Видео:Площадь параллелограмма треугольника и трапецииСкачать

Признаки параллелограмма
AB||CD, AB = CD (или BC||AD, BC = AD)
∠DAB = ∠BCD, ∠ABC = ∠CDA
∠ABC + ∠BCD = ∠BCD + ∠CDA = ∠CDA + ∠DAB = ∠DAB + ∠DAB = 180°
AC 2 + BD 2 = AB 2 + BC 2 + CD 2 + AD 2
Видео:Площадь параллелограмма, треугольника, трапецииСкачать

Основные свойства параллелограмма
∠ABC = ∠CDA, ∠BCD = ∠DAB
∠ABC + ∠BCD + ∠CDA + ∠DAB = 360°
∠ABC + ∠BCD = ∠BCD + ∠CDA = ∠CDA + ∠DAB = ∠DAB + ∠DAB = 180°
8. Диагонали параллелограмма пересекаются и точкой пересечения делят друг друга пополам:
| AO = CO = | d 1 |
| 2 | |
| BO = DO = | d 2 |
| 2 |
AC 2 + BD 2 = 2AB 2 + 2BC 2
Видео:Площадь треугольника. Как найти площадь треугольника?Скачать

Стороны параллелограмма
Формулы определения длин сторон параллелограмма:
1. Формула сторон параллелограмма через диагонали и угол между ними:
2. Формула сторон параллелограмма через диагонали и другую сторону:
| a = | √ 2 d 1 2 + 2 d 2 2 — 4 b 2 |
| 2 |
| b = | √ 2 d 1 2 + 2 d 2 2 — 4 a 2 |
| 2 |
3. Формула сторон параллелограмма через высоту и синус угла:
| a = | h b |
| sin α |
| b = | h a |
| sin α |
4. Формула сторон параллелограмма через площадь и высоту:
| a = | S |
| ha |
| b = | S |
| hb |
Видео:8 класс, 13 урок, Площадь параллелограммаСкачать

Диагонали параллелограмма
Формулы определения длины диагонали параллелограмма:
d 1 = √ a 2 + b 2 — 2 ab·cosβ
d 2 = √ a 2 + b 2 + 2 ab·cosβ
d 1 = √ a 2 + b 2 + 2 ab·cosα
d 2 = √ a 2 + b 2 — 2 ab·cosα
d 1 = √ 2 a 2 + 2 b 2 — d 2 2
d 2 = √ 2 a 2 + 2 b 2 — d 1 2
4. Формула диагонали параллелограмма через площадь, известную диагональ и угол между диагоналями:
| d 1 = | 2S | = | 2S |
| d 2· sinγ | d 2· sinδ |
| d 2 = | 2S | = | 2S |
| d 1· sinγ | d 1· sinδ |
Видео:Параллелограмм. Практическая часть - решение задачи. 8 класс.Скачать

Периметр параллелограмма
Формулы определения длины периметра параллелограмма:
P = 2 a + 2 b = 2( a + b )
P = 2 a + √ 2 d 1 2 + 2 d 2 2 — 4 a 2
P = 2 b + √ 2 d 1 2 + 2 d 2 2 — 4 b 2
3. Формула периметра параллелограмма через одну сторону, высоту и синус угла:
| P = | 2( b + | h b | ) |
| sin α |
| P = | 2( a + | h a | ) |
| sin α |
Видео:Как найти площадь треугольника без формулы?Скачать

Площадь параллелограмма
Формулы определения площади параллелограмма:
3. Формула площади параллелограмма через две диагонали и синус угла между ними:
| S = | 1 | d 1 d 2 sin γ |
| 2 |
| S = | 1 | d 1 d 2 sin δ |
| 2 |
Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!
Добро пожаловать на OnlineMSchool.
Меня зовут Довжик Михаил Викторович. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики.
Параллелограмм – четырехугольник с попарно параллельными противоположными сторонами.
Противолежащие стороны параллелограмма имеют одинаковую длину. Периметр параллелограмма находят как удвоенную сумму двух его сторон:
Формулы для вычисления длины периметра параллелограмма:
1. Формула периметра параллелограмма через стороны параллелограмма:
P = 2a + 2b = 2(a + b);
2. Формула периметра параллелограмма через 1-ну сторону и 2-е диагонали:
3. Формула периметра параллелограмма через 1-ну сторону, высоту и sin угла:
Свойства параллелограмма:
1. Противоположные стороны равны и параллельны
2. Противоположные углы равны
3. Точка пересечения диагоналей, делит их пополам
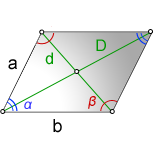
1. Длина диагонали параллелограмма через стороны, известную диагональ и угол.
a , b — стороны параллелограмма
D — большая диагональ
d — меньшая диагональ
α , β — углы параллелограмма
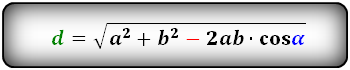
Формулы диагонали через стороны и углы параллелограмма (по теореме косинусов), ( D , d ):
Формулы диагонали через стороны и известную диагональ (по формуле- сумма квадратов диагоналей), ( D , d ):
2. Длина диагонали параллелограмма через площадь, известную диагональ и угол.
D — большая диагональ
d — меньшая диагональ
α , β — углы между диагоналями
S — площадь параллелограмма
Формулы диагонали через площадь, известную диагональ и угол между диагоналями, ( D , d ):
Видео:Свойства параллелограмма. Все задачи на периметр. Геометрия 8 классСкачать

Как найти периметр квадрата, прямоугольника, параллелограмма, трапеции, ромба, эллипса, многоугольника
Вы будете перенаправлены на Автор24
Периметр любой геометрической фигур на плоскости определяется как сумма длин всех его сторон. В этой статье, на примере задач, мы приведем формулы для нахождения периметров квадрата, прямоугольника, параллелограмма, трапеции, ромба, многоугольника и эллипса.
Видео:Площади фигур - треугольника, параллелограмма, трапеции, ромба. Формула Пика и ЕГЭСкачать

Периметр квадрата
Квадратом будем назвать такую геометрическую фигуру, которая состоит из четырех равных сторон, все углы которой прямые (рис. 1).
Найти периметр квадрата, если его сторона равняется $α$.
Так как все 4 стороны квадрата равны между собой, то, по определению периметра, получим
Вывод: Для нахождения периметра квадрата надо длину его стоны умножить на $4.$
Видео:Запомни: все формулы для площади треугольникаСкачать

Периметр прямоугольника
Прямоугольником будем назвать такую геометрическую фигуру, которая состоит из четырех сторон, причем противоположные стороны равны между собой, все углы которой прямые (рис. 2).
Найти периметр прямоугольника, если его смежные стороны равняются $α$ и $β$.
Так как противоположные стороны равняются между собой, то
Готовые работы на аналогичную тему
Вывод: Для нахождения периметра прямоугольника надо сумму длин его смежных сторон умножить на $2.$
Видео:Геометрия 8 класс (Урок№10 - Площадь треугольника.)Скачать

Периметр параллелограмма
Параллелограммом будем назвать такую геометрическую фигуру, которая состоит из четырех сторон, причем противоположные стороны равны между собой и параллельны друг другу (рис. 3).
Найти периметр параллелограмма, если его смежные стороны равняются $α$ и $β$.
Так как противоположные стороны равняются между собой, то
Вывод: Для нахождения периметра параллелограмма надо сумму длин его смежных сторон умножить на $2.$
Видео:КАК НАЙТИ ПЕРИМЕТР ТРЕУГОЛЬНИКА? Примеры | МАТЕМАТИКА 5 классСкачать

Периметр трапеции
Трапецией будем назвать такую геометрическую фигуру, которая состоит из четырех сторон, причем 2 противоположные стороны, которые называются основаниями, параллельны друг другу (рис. 4).
Найти периметр трапеции, если его стороны равняются $α$, $β$, $γ$ и $δ$.
По определению периметра плоской геометрической фигуры получим, что
Вывод: Для нахождения периметра трапеции надо сложить все длины его сторон.
Видео:8 класс, 14 урок, Площадь треугольникаСкачать

Периметр ромба
Ромбом будем назвать такой параллелограмм, у которого все стороны равны между собой (рис. 5).
Найти периметр ромба, если его сторона равняется $α$.
Так как все 4 стороны ромба равны между собой, то, по определению периметра, получим
Вывод: Для нахождения периметра ромба надо длину его стоны умножить на $4.$
Видео:Как вычислить периметр #геометрия #задача #треугольник #периметрСкачать

Периметр многоугольника
Отметим, что все фигуры, рассмотренные выше, являются многоугольниками, а именно четырехугольниками. Поэтому можем рассмотреть более обще понятие, а именно понятие -угольника.
$n$-угольником будем назвать такую геометрическую фигуру, которая состоит из $n$ непересекающихся сторон и $n$ углов. (рис. 6).
Найти периметр $n$-угольника, если его стороны равняются $α_1$, $α_2$,…, $α_n$.
По определению периметра плоской геометрической фигуры получим, что
Вывод: Для нахождения периметра -угольника надо сложить все длины его сторон.
Здесь можно выделить периметр правильного $n$-угольника, то есть $n$-угольника, у которого все стороны равняются между собой.
Найти периметр правильного $n$-угольника, если его сторона равняется $α$.
Так как все $n$ сторон правильного $n$-угольника равны между собой, то, по определению периметра, получим
Вывод: Для нахождения периметра правильного $n$-угольника надо длину его стороны умножить на $n$
Видео:8 класс, 4 урок, ПараллелограммСкачать

Периметр эллипса
Здесь просто введем формулу, для вычисления периметра (или еще иначе длины) эллипса. Пусть нам дан эллипс, как на рисунке 7.
Тогда периметр эллипса равняется
Получи деньги за свои студенческие работы
Курсовые, рефераты или другие работы
Автор этой статьи Дата последнего обновления статьи: 13 07 2021
Эксперт по предмету «Геометрия»
Работаем по будням с 10:00 до 20:00 по Мск
. и многие другие.
Успешной учебы! Будем рады вам помочь!
📽️ Видео
№372. Периметр параллелограмма равен 48 см. Найдите стороны параллелограмма, если: аСкачать

Урок. Как найти периметр треугольника. Математика 2 класс. #учусьсамСкачать

ОГЭ 23 КАК НАЙТИ ПЕРИМЕТР ПАРАЛЛЕЛОГРАММА Если известны отрезки, на которые делитсторону биссектрисаСкачать