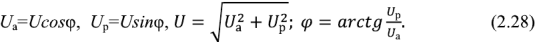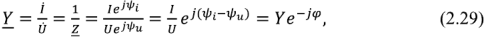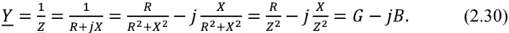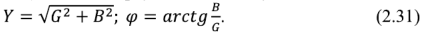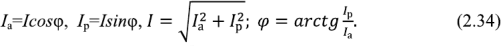На рис. 24.1 показан пассивный двухполюсник, состоящий из активных и реактивных элементов. Действующие значения напряжения U, тока I и угол сдвига фаз между ними φ известны.
Рис. 24.1 — Пассивный двухполюсник
Построим по этим значениям векторную диаграмму и, спроектировав вектор напряжения на вектор тока и перпендикулярное к нему направление, получим треугольник напряжений, образованный сторонами Ua, Up, U (рис. 24.2 а).
Схема называется последовательной схемой замещения или последовательной эквивалентной схемой пассивного двухполюсника, а ее параметры R , X и Z – эквивалентными сопротивлениями двухполюсника.
Рис. 24.2 — Векторная диаграмма и соответствующая ей последовательная экв. сх.
Треугольник, образованный сторонами R, X, Z и подобный треугольнику напряжений, представляет собой треугольник сопротивлений
Теперь разложим вектор тока на две составляющие Ia – активную , направленную по вектору напряжения, и реактивную Ip, перпендикулярную к нему (рис. 24.3, а). Такой векторной диаграмме соответствует параллельная схема замещения двухполюсника (рис. 24.3, б). Ее параметры G, B и Y называются эквивалентными проводимостями. Токи в элементах G и B мы и представляем как активную и реактивную составляющие общего тока: Ia=GU, Ip=BU. Из треугольника токов (рис. 24.3, а) получается треугольник проводимостей.
Рис. 24.3 — Паралельная эквивалентная схема и ее векторная диаграмма
Получим условия эквивалентности приведенных схем.
Для последовательной цепи U=IZ, для параллельной I=YU, а так как токи и напряжения в обеих схемах одинаковы, то: Y=1/Z и Z=1/Y
т.е. в любой электрической цепи полная проводимость есть величина, обратная полному сопротивлению.
Формулы перехода от последовательной эквивалентной схемы к параллельной:
Формулы перехода от параллельной эквивалентной схемы к последовательной:
Обращаем внимание на то, что каждая из проводимостей G и B зависит от обоих сопротивлений – активного и реактивного. В свою очередь, каждое из сопротивлений определяется обеими проводимостями. Соотношения G = 1/R и B = 1/x справедливы только в частном случае, первое – при х = 0, второе – при R = 0.
Следует отметить, что активная и реактивная составляющие напряжения и тока физически не существуют, измерить их нельзя. Они относятся только к соответствующим эквивалентным схемам замещения и находятся расчетом. Более того, проектируя, например, вектор тока на различные напряжения, мы получим для него разные составляющие.
Видео:Цепи переменного тока. Комплексные значения сопротивлений, токов и напряжений в цепи. Задача 1Скачать

Понятие входного сопротивления пассивного двухполюсника и его простейшая схема замещения
Любая цепь, имеющая два зажима, является двухполюсником. Если внутри двухполюсника нет источников, то он называется пассивным и обозначается, как показано на рис. 2.3, а. Токи в ветвях пассивного двухполюсника могут возникать только при наличии внешних воздействий.
Рис. 23. Пассивный двухполюсник:
а — общее изображение; б — простейшая схема замещения; в — пассивный двухполюсник с параллельно-последовательным соединением элементов
Входным сопротивлением пассивного двухполюсника называется величина, равная отношению напряжения к току на его входе: RBX = U/I.
Для линейного двухполюсника (рис. 2.3, б) RBX — его параметр, определяемый схемой и величиной сопротивлений элементов. От напряжения, созданного на его входе, RBX не зависит. Входное сопротивление можно определить экспериментально методом амперметра-вольтметра.
Если известна схема двухполюсника, то возможен расчетный путь. Например, для двухполюсника на рис. 2.3, в
Здесь учтено, что параллельно включенные R3 и Т?4 последовательны с Я, и R,.
Если соединение элементов в схеме двухполюсника не является параллельно-последовательным (рис. 2.4), его входное сопротивление может быть найдено по законам Кирхгофа. Для этого рассчитываем ток входной ветви, соответствующий произвольно заданному напряжению на входе.
Рис. 2.4. Схема пассивного двухполюсника, которая не является параллельно-
В таких случаях при определении RBX возможно также применение преобразования пассивных трехполюсников [4].
По отношению к внешней цени пассивный двухполюсник может быть заменен одним элементом — резистором RBX. Поэтому можно утверждать, что простейшая схема замещения пассивного двухполюсника содержит один элемент — резистор RBX (см. рис. 2.3, б).
Видео:Построение векторных диаграмм/Треугольник токов, напряжений и мощностей/Коэффициент мощностиСкачать

Пассивный двухполюсник
Двухполюсник — участок цени, имеющий два внешних зажима (полюса), которыми он подключается к остальной цепи. Пассивным называется двухполюсник, не содержащий источников электрической энергии.
Если внутренняя схема соединений двухполюсника неизвестна или раскрытие ее не требуется, двухполюсник изображается в виде прямоугольника с двумя зажимами (рис. 2.10,а).
При анализе электрической цепи, в которую входит двухполюсник, достаточно знать его характеристику, в качестве которой берут так называемое внутреннее или входное сопротивление. Напряжение и ток в точках подключения двухполюсника называются входным напряжением и входным током.
Пусть входное напряжение двухполюсника 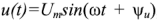
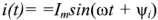
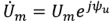
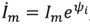
является комплексным сопротивлением двухполюсника. Комплексное сопротивление 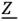
Здесь 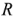
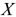
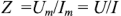
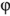
Выражение (2.26) показывает, что схема замещения пассивного двухполюсника может быть представлена последовательно соединенными активным сопротивлением 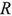
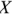
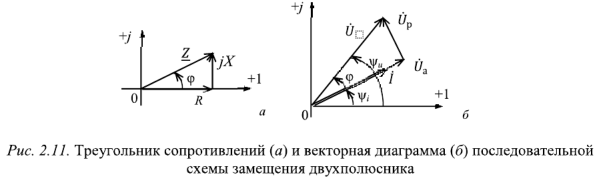
Активное сопротивление всегда положительно, а реактивное может иметь любой знак. Если составляющие комплексного сопротивления изобразить векторами на плоскости, то активное, реактивное и полное сопротивления образуют прямоугольный треугольник, называемый треугольником сопротивлений. Треугольник сопротивлений для 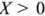
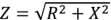
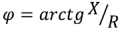
При отсутствии активной составляющей комплексного входного сопротивления двухполюсника 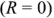
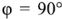
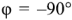
При наличии активной составляющей 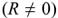
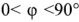
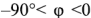
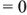
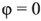
В соответствии с (2.25) и (2.26)
Из (2.27) следует, что комплексное напряжение на входе двухполюсника состоит из двух составляющих. Одна из них 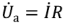
Вторая
— перпендикулярна току и называется комплексным реактивным напряжением.
Соотношения (2.27) соответствуют последовательной схеме замещения пассивного двухполюсника (рис. 2.10,6). Напряжение на активном сопротивлении этой схемы соответствует активному напряжению 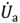
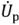
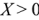
Для составляющих комплексного напряжения очевидны соотношения
Соотношение между током и напряжением на входе двухполюсника можно определить так же и с помощью понятия комплексной проводимости
где 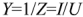
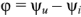
Подставив в выражение (2.29) 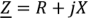
Вещественная часть 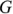
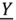
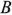
Выражение (2.30) показывает, что схема замещения пассивного двухполюсника может быть представлена параллельно соединенными активной проводимостью 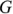
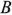
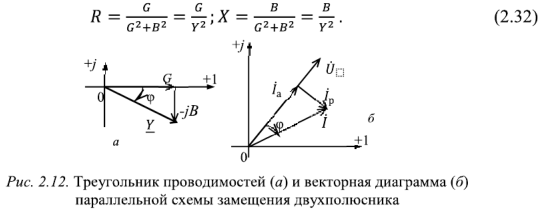
На комплексной плоскости комплексная проводимость и её составляющие образуют прямоугольный треугольник, называемый треугольником проводимостей (рис. 2.12,а). Из этого треугольника следует:
Выражение (2.30) позволяет выразить составляющие комплексной проводимости пассивного двухполюсника через составляющие его комплексного сопротивления:
В соответствии с первым законом Кирхгофа для параллельной схемы замещения пассивного двухполюсника (рис.2.10,в) можно записать
Вектор комплексного активного тока 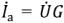
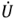
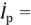
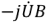
Для активной и реактивной составляющих комплексного тока очевидны соотношения:
При этом активный ток может быть только положительным, а знак реактивного тока определяется знаком фазового сдвига ф.
Рассмотренные параллельная и последовательная схемы замещения пассивного двухполюсника (рис. 2.10) полностью эквивалентны, а активное и реактивное сопротивления, активная и реактивная проводимости являются параметрами двухполюсника.
Эта теория взята со страницы помощи с заданиями по электротехнике:
Возможно эти страницы вам будут полезны:




















































Образовательный сайт для студентов и школьников
Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.
© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института
🔍 Видео
лекция 9. Метод Активного двухполюсникаСкачать

Как снять векторную диаграммуСкачать
Лекция по электротехнике 4.1 - Двухполюсник. Треугольники сопротивлений и проводимостейСкачать

Векторная диаграмма токов и топографическая диаграмма напряженийСкачать

Зачем нужны векторные диаграммы?Скачать

Как построить векторную диаграмму напряжений?Скачать
Векторные диаграммы и коэффициент мощностиСкачать

ТОЭ│Задача на переменный ток. Определить сопротивления элементов. Векторная диаграммаСкачать

Лекция по электротехнике 4.2 - Двухполюсник. Временные и векторные диаграммыСкачать

Построение векторной диаграммы. Цепь RLCСкачать

РЕТОМЕТР-М2.СНЯТИЕ ВЕКТОРНЫХ ДИАГРАММ.ОСНОВЫ РАБОТЫ С ВАФом.ЭНЕРГЕТИКА И РЕЛЕЙНАЯ ЗАЩИТА.ЭТЛ.Скачать

Олимпиадная задача по ТОЭ #1. Активные двухполюсники│Постоянный токСкачать

Двухфазное КЗ на векторных диаграммахСкачать

Векторная диаграммаСкачать

Векторная диаграмма токов на комплексной плоскости вручнуюСкачать

Расчет RLC цепи переменного тока │Построить векторную диаграмму, определить показание вольтметраСкачать

Векторная диаграмма - как она строится без чисел по схемеСкачать

Векторные диаграммы Токов и Напряжений в программе VisioСкачать










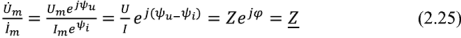
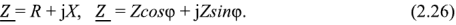
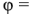
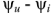
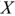
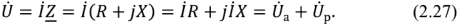
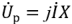 — перпендикулярна току и называется комплексным реактивным напряжением.
— перпендикулярна току и называется комплексным реактивным напряжением.