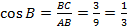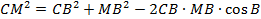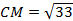Доказательство теоремы косинусов через окружность

О чем эта статья:

Видео:ТЕОРЕМА СИНУСОВ И ТЕОРЕМА КОСИНУСОВ. Тригонометрия | МатематикаСкачать

Формулировка и доказательство теоремы косинусов

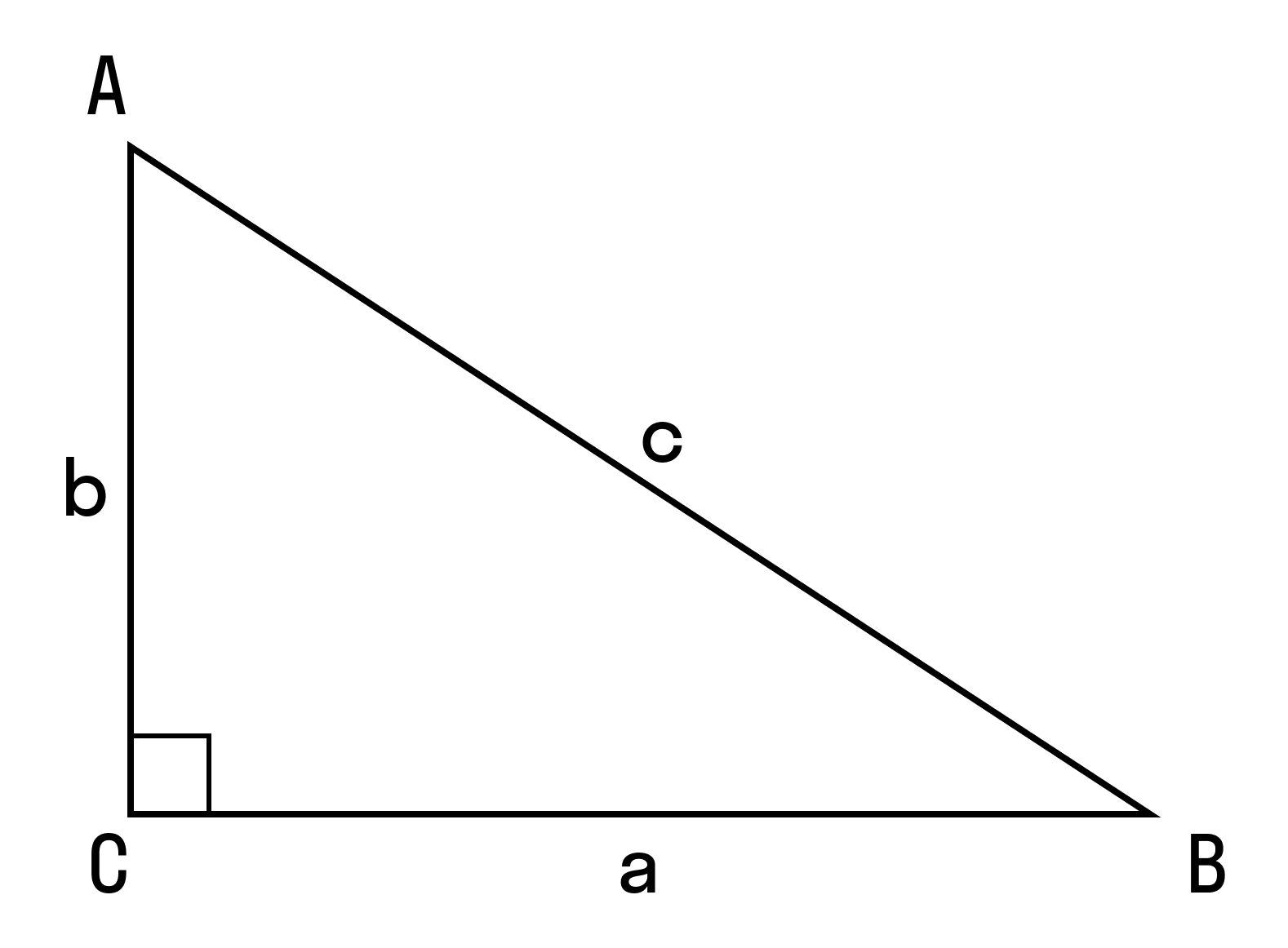
Для начала вспомним теорему Пифагора: в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.

Формула Теоремы Пифагора:

a 2 > + b 2 > = c 2 >, где a, b — катеты, с — гипотенуза.

Теорема косинусов звучит так: квадрат стороны треугольника равен сумме квадратов двух других его сторон минус удвоенное произведение этих сторон на косинус угла между ними.

Формула теоремы косинусов:

a 2 = b 2 + c 2 — 2bc cos α

В доказательстве теоремы косинусов используем формулу длины отрезка в координатах. Рассмотрим данную формулу:

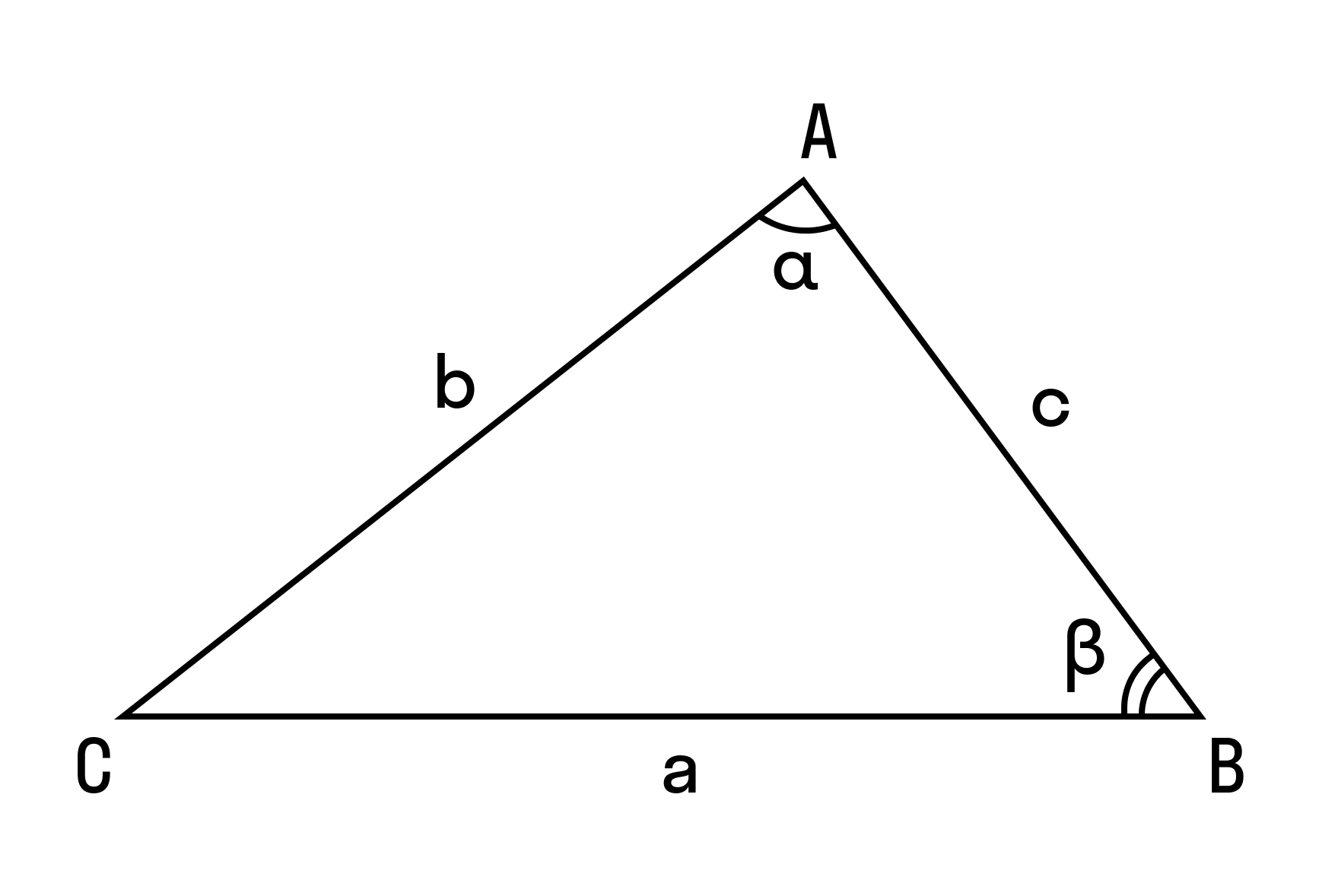
В доказательстве теоремы косинусов BC — это сторона треугольника АВС, которая обозначена буквой а. Введем удобную систему координат и найдем координаты нужных нам точек. У точки В координаты (с; 0).
Координаты точки С — (b cos α; b sin α) при α ∈ (0° ; 180°).

BC 2 = a 2 = (b cos α — c) 2 + b 2 sin 2 α = b 2 cos 2 α + b 2 sin 2 α — 2bc cos α + c 2 = b 2 (cos 2 α + sin 2 α) — 2bc cos α + c 2

cos 2 α + sin 2 α = 1 — основное тригонометрическое тождество.

Что и требовалось доказать.

Совет: чтобы быстрее разобраться в сложной теме, запишитесь на онлайн-курсы по математике для детей и подростков.

С помощью теоремы косинусов можно найти косинус угла треугольника:

• Когда b 2 + c 2 — a 2 > 0, угол α будет острым.
• Когда b 2 + c 2 — a 2 = 0, угол α будет прямым.
• Когда b 2 + c 2 — a 2

Сформулируем еще одно доказательство теоремы косинусов.

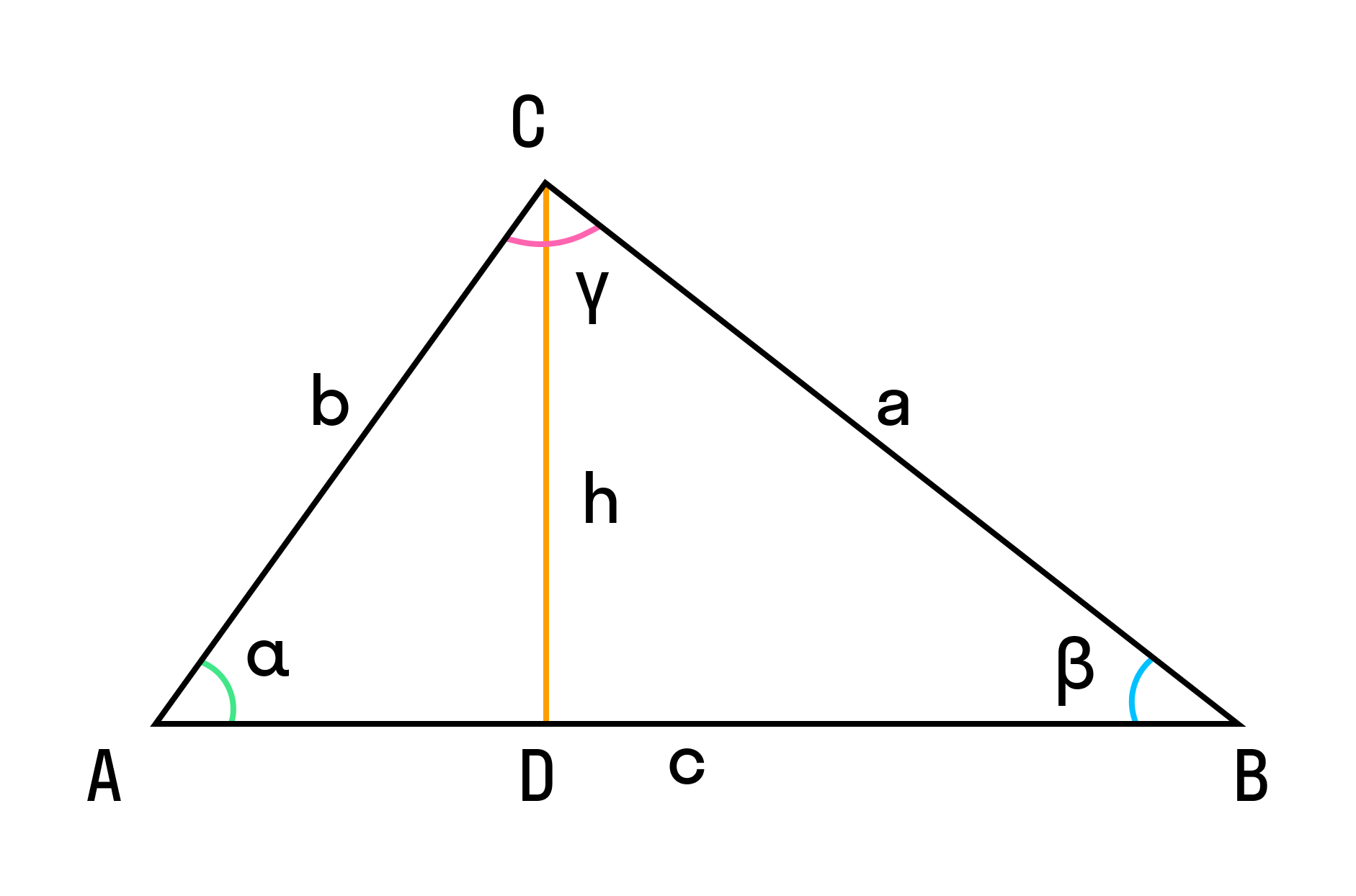
Пусть нам дан треугольник ABC, в котором из вершины C на сторону AB опустили высоту CD. Это значит:

• AD = b × cos α,
• DB = c – b × cos α.

Запишем теорему Пифагора для двух прямоугольных треугольников ADC и BDC:

• h 2 = b 2 — (b × cos α) 2
• h 2 = a 2 — (c – b × cos α) 2

Приравниваем правые части уравнений:

• b 2 — (b × cos α) 2 = a 2 — (c — b × cos α) 2

• a 2 = b 2 + c 2 — 2bc × cos α

Если один из углов при основании тупой (высота упирается в продолжение основания), полностью аналогичен рассмотренному выше.

Определим стороны b и c:

• b 2 = a 2 + c 2 — 2ac × cos β;
• c 2 = a 2 + b 2 — 2ab × cos γ.

Видео:#233. Теоремы синусов и косинусов | Формулы радиусов окружностейСкачать

Формулировка теоремы для каждой из сторон треугольника

Теорема косинусов справедлива для всех сторон треугольника, то есть:

a 2 = b 2 + c 2 — 2bc cos α

b 2 = c 2 + a 2 — 2ca cos β

c 2 = a 2 + b 2 — 2ab cos γ

Теорема косинусов может быть использована для любого вида треугольника.

Видео:Теоремы синусов и косинусов | Ботай со мной #029 | Борис ТрушинСкачать

Косинусы углов треугольника

Теорема косинусов позволяет найти как косинус, так и угол треугольника. Найдём косинусы углов:

Видео:Геометрия. 9 класс. Теорема синусов /26.01.2021/Скачать

Определение угла с помощью косинуса

А теперь обратим внимание на углы.

Как мы уже знаем, косинус угла из промежутка (0°; 180°) определяет угол (в отличие от его синуса).

Пусть нам дана единичная полуокружность. Если нам задан cos α, то нам задана точка на верхней полуокружности и задан угол α. Следовательно, cos α однозначно определяет точку М(cos α; sin α), и однозначно определяется угол ∠AOM.

Видео:9 класс, 14 урок, Теорема косинусовСкачать

Рассмотрение пределов изменения cos α и sin α

Рассмотрим пределы изменения синуса и косинуса α. Вспомним, что если α — угол треугольника, то он лежит в пределах от 0° до 180°.

Предел изменения косинуса: -1 0, то α ∈ (0°;90°)
Если cos α

Видео:Теорема косинусов #shortsСкачать

Примеры решения задач

При помощи теоремы косинусов можно решать задачки по геометрии. Рассмотрим интересные случаи.

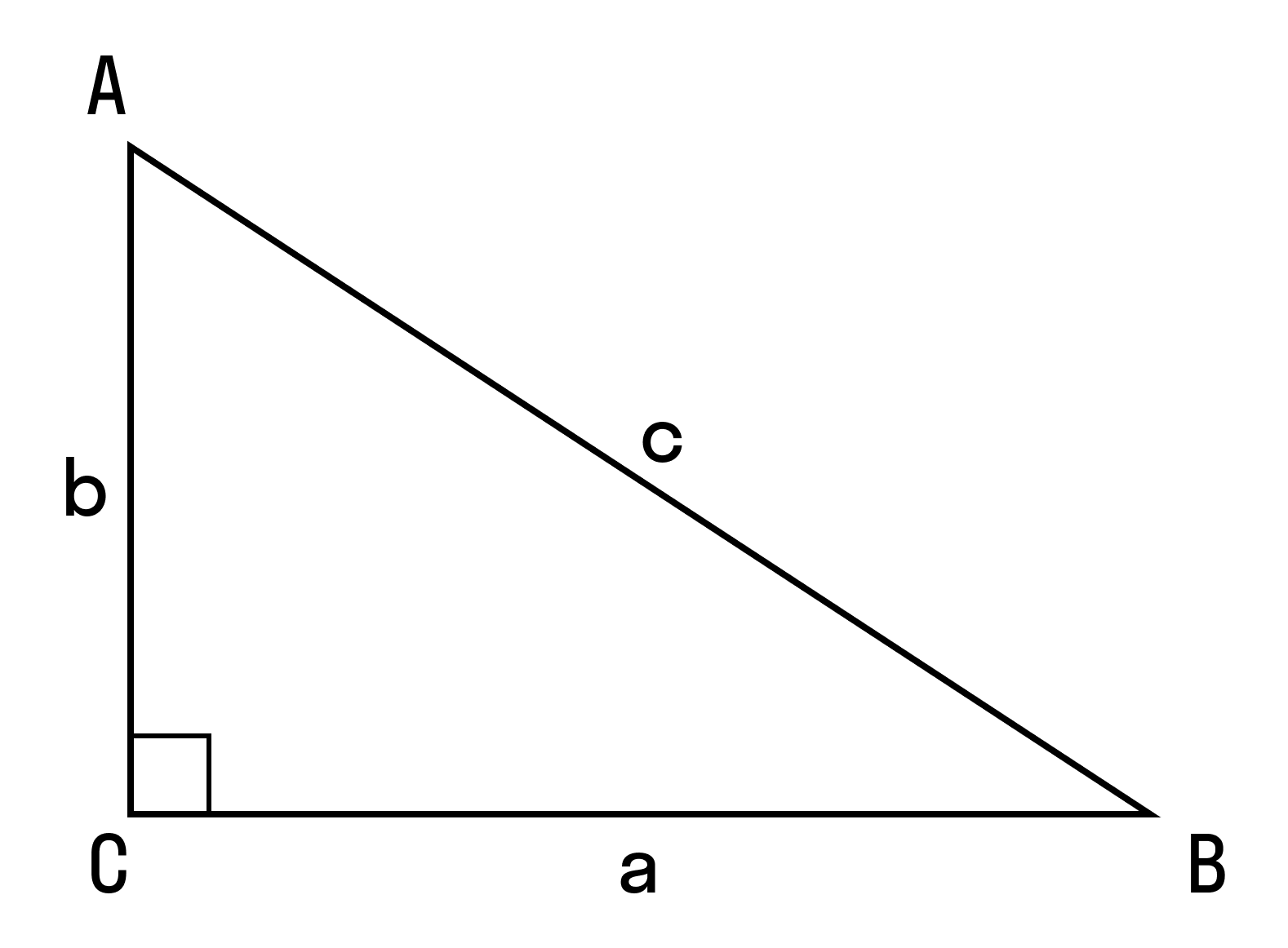
Пример 1. Дан треугольник АВС. Найти длину СМ.

∠C = 90°, АВ = 9, ВС = 3, AM/MB = 1/2, где М — точка на гипотенузе АВ.

Так как АМ + МВ = 9, а AM/MB = 1/2, то АМ = 3, МВ = 6.
Из треугольника АВС найдем cos B:

Из треугольника СМВ по теореме косинусов найдём СМ:

Пример 2. Дан треугольник АВС, в котором a2+ b22 + b 2 2 , то cos C 2 = a 2 + b 2 , то ∠C = 90°.

• Если c 2 2 + b 2 , то ∠C — острый.

Видео:Теорема синусов и теорема косинусовСкачать

Теорема косинусов. Доказательство теоремы косинусов.

Теорема косинусов — теорема евклидовой геометрии, которая обобщающает теорему Пифагора.

Теорема косинусов:

Для плоского треугольника, у которого стороны a, b, c и угол α, который противолежит стороне a, справедливо соотношение:

Квадрат стороны треугольника равняется сумме квадратов 2-х других сторон минус удвоенное произведение этих сторон на косинус угла между ними.

Видео:Теорема косинусов | ДоказательствоСкачать

Следствие из теоремы косинусов.

• Теорема косинусов используется для определения cos угла треугольника:

h 2 = a 2 — (c – b cos α) 2 (2)

Приравниваем правые части уравнений (1) и (2):

b 2 — (b cos α) 2 = a 2 — (c — b cos α) 2

a 2 = b 2 + c 2 — 2bc cos α.

Если 1-н из углов при основании тупой (высота упирается в продолжение основания), полностью аналогичен рассмотренному выше.

Определить стороны b и c:

Видео:Теорема синусов – просто и красиво // Vital MathСкачать

Теорема косинусов

Чтобы найти строну или угол треугольника применяют Теорему Косинусов.
Эта теорема обобщает теорему Пифагора. Доказать Теорему
Косинусов достаточно просто через треугольник, который
разделяют высотой на два прямоугольных треугольника.

Мы рассмотрим доказательство, формулировку,
следствия из Теоремы Косинусов.

Наряду с одной из известных теорем геометрии — теоремой Пифагора,
существует теорема косинусов. Теорема косинусов похожа по теорему
Пифагора, но отличается. Теорему косинусов, можно применить к абсолютно
любым треугольникам. А теорема Пифагора применяется исключительно
для прямоугольных треугольников.

Теорема косинусов — это теорема геометрии, обобщающая
теорему Пифагора, применяющаяся при нахождении углов
и сторон в любых треугольниках.

Видео:Теорема КосинусовСкачать

Формулировка теоремы косинусов

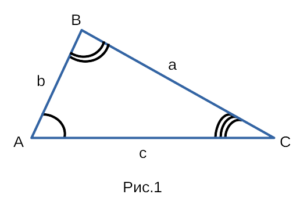
Формулировка у теоремы косинусов такая: в треугольнике квадрат любой из сторон
равен сумме квадратов двух других сторон минус удвоенное
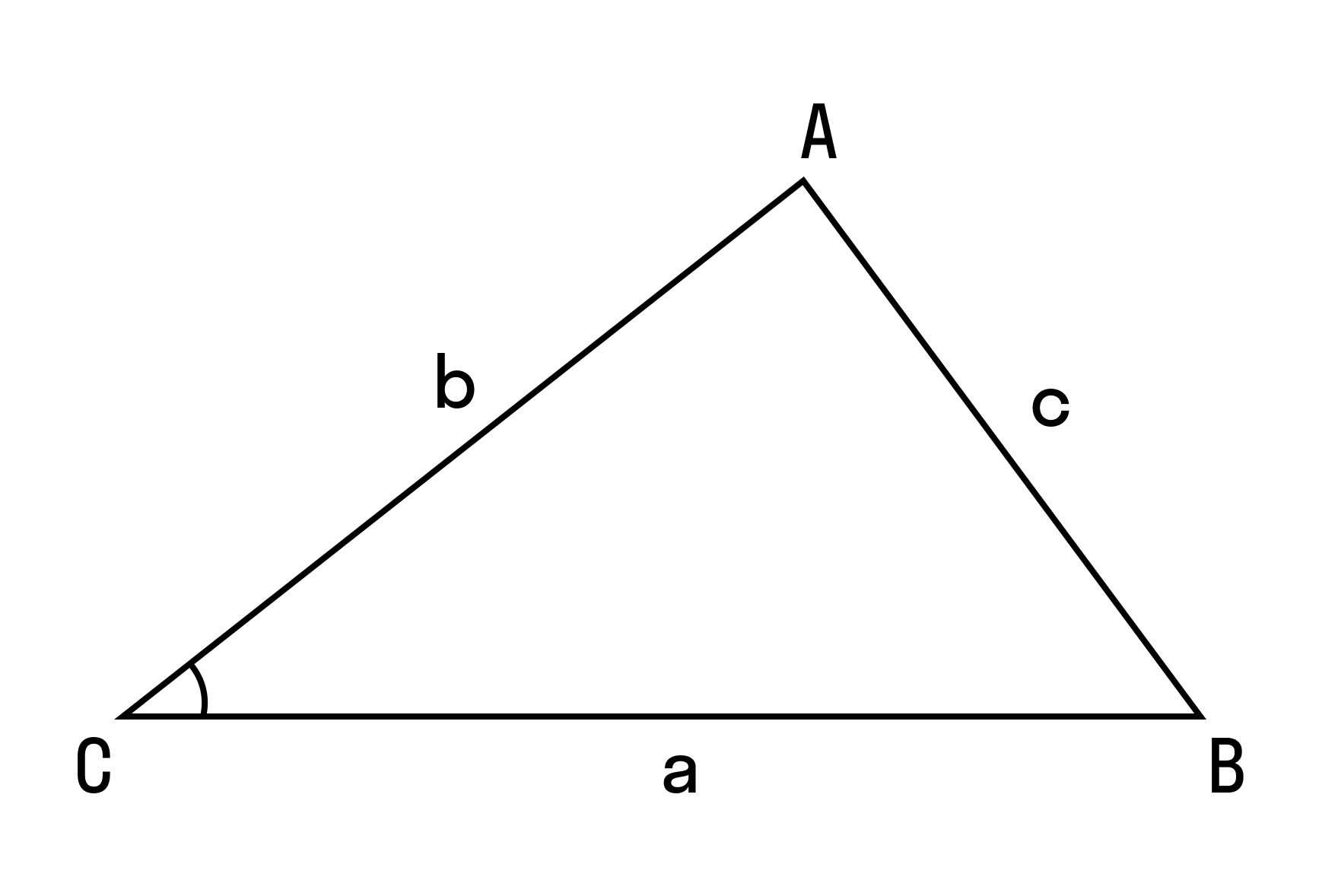
произведение этих сторон на косинус угла между ними. Запишем эту
формулировку более кратко, используя рисунок 1, на котором изображен
произвольный треугольник ABC:​ ( BC^2 = AB^2 + AC^2 — 2 * (AB * AC) * cos ∠A ) ​.
Или, же еще более кратко: ​ ( a^2 = b^2 + c^2 — 2bc * cos ∠A ) ​.

Видео:Теорема, которую не могли доказать 350 лет — за 900 секунд // Великая теорема ФермаСкачать

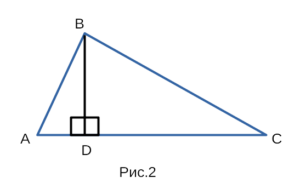
Доказательство теоремы косинусов

Для доказательства теоремы косинусов воспользуемся
рисунком 2, на котором изображен треугольник ABC.

Докажем, что ​ ( BC^2 = AB^2 + AC^2 — 2 * (AB * AC) * cos ∠A: )

1. Доп. построение: высота BD.
2. Рассмотрим △BDC:
   ​ ( BC^2= BD^2 + DC^2. )
3. Рассмотрим △ABD:
   ​ ( AD = AB * cos ∠A, ) ​
   ​ ( BD = AB * sin ∠A, ) ​
   ​ ( CD = AC — AD = AC — AB cos ∠A. ) ​
4. Из всего этого следует, что: ​
   ( ВС^2 = (AB * sin ∠A)^2 + (AC — AB * cos ∠A)^2 = ) ​
   ( AB^2 * sin^2 ∠A + AC^2 — 2AB * AC * cos ∠A + AB^2 * cos^2 ∠A = )
   ( AB^2 + AC^2 — 2 * (AB*AC) * cos ∠A. )
   Следовательно, ​ ( BC^2 = AB^2 + AC^2 — 2 * (AB * AC) * cos ∠A. ) ​ч.т.д.
5. Теорема косинусов доказана.

Видео:Шаталов за одну минуту доказывает теорему, на которую традиционно выделяется 45 минут урока!Скачать

Следствия из теоремы косинусов

1. Квадрат любой из сторон треугольника равен сумме квадратов двух
   других сторон минус удвоенное произведение этих
   сторон на косинус угла между ними.
2. ​ ( a^2 = b^2 + c^2 — 2bc * cos ∠A ) ​;
   ​ ( b^2 = c^2 + a^2 — 2ca * cos ∠B ) ​;
   ​ ( c^2 = a^2 + b^2 — 2ab * cos ∠C ) ​;
3. Так, как в прямоугольном треугольнике один из углов равен 90 градусам,
   следовательно теорема косинусов преобразуется в теорему Пифагора.
4. С помощью теоремы косинусов, можно определить косинус
   любого из углов треугольника.
5. Если, b 2 + c 2 — a 2 > 0, ∠A будет острый.
   Если b2+c2—a2= 0, ∠A будет прямым.
   Если b2+c2—a2∠A будет тупым.

Видео:Подобие треугольников. Признаки подобия треугольников (часть 1) | МатематикаСкачать

Значение теоремы косинусов

Где применяется теорема косинусов?

Теорема косинусов применяется в тригонометрии, в частности
при нахождение сторон и углов в любых треугольниках. Например, зная
формулировку теоремы косинусов, косинус одно из угла треугольника,
и две стороны можно найти неизвестную сторону треугольника.

Виды теорем косинусов.

В зависимости от свойств треугольника, длины его сторон, градусной меры
его углов — теорема косинусов немного видоизменяется. Например, в
прямоугольных треугольниках теорема косинусов преобразуется в теорему Пифагора.

🔥 Видео

Теорема синусов с доказательствомСкачать

Теорема косинусов. Легче уже не доказать #егэ2023 #математика #егэ #школа #shorts #fypСкачать

Подготовка к ОГЭ. Теорема синусов. Доказательство.Скачать

Теорема косинусовСкачать

9 класс, 13 урок, Теорема синусовСкачать

ЛУЧШЕЕ ДОКАЗАТЕЛЬСТВО теоремы СинусовСкачать

Теорема косинусов с доказательствомСкачать