Прототипы заданий 16 ОГЭ по математике. Материал для подготовки к ОГЭ.
Для выполнения задания 16 необходимо уметь выполнять действия с геометрическими фигурами, координатами и векторами (окружность, круг и их элементы )
Подробнее узнать виды заданий на данной позиции в КИМах можно по кодификатору
| Карточки для отработки задания 16 с ответами → скачать |
| Прототипы задания 16 ОГЭ по математике (окружности) Опубликовано: Гармс Людмила Павловна → скачать |
| Материалы для отработки задания 16 Автор: Е. А. Ширяева → задания |
| Задания 16 — практика Решение типовых задач № 16 на ОГЭ по математике Содержание Видео:Углы в окружности. 16 задание ОГЭ математика 2023 | Молодой РепетиторСкачать  Как решать 16 задание в огэ по математике окружностьБоковая сторона равнобедренного треугольника равна 4. Угол при вершине, противолежащий основанию, равен 120°. Найдите диаметр окружности, описанной около этого треугольника. Воспользуемся теоремой косинусов: (здесь a и b — боковые стороны равнобедренного треугольника, c — основание. Диаметр описанной окружности найдем по обобщенной теореме синусов: Вместо того, чтобы искать основание треугольника, можно было найти угол при основании. Действительно, сумма углов при основании данного равнобедренного треугольника равна 60°. Эти углы равны, поэтому каждый из них равен 30°. Применяя обобщенную теорему синусов для боковой стороны и противолежащего ей угла, получаем: Приведем решение Андрея Ларионова. Угол при основании равен Следовательно, дуга описанной окружности, на которую он опирается, равна 2 · 30° = 60°. Эту дугу стягивает боковая сторона треугольника. Хорда, стягивающая дугу в 60°, равна радиусу окружности, поэтому радиус описанной окружности равен боковой стороне треугольника, тогда D = 2 · 4 = 8. Видео:Задание 16 ОГЭ 2023 математика | Окружность, круг и их элементыСкачать  Задание №16 ОГЭ по математикеВ 16 задании ОГЭ по математике необходимо решить простую задачу по геометрии. Для успешного решения необходимо обладать базовыми знаниями по геометрии вообще, так как сложно выделить какую-то одну тему, по которой даны задания. Это относится ко всему модулю геометрии. Я рекомендую повторить понятия центральные и вписанные углы, свойства касательных к окружности, взаимосвязь между радиусом описанной или вписанной окружности в геометрические фигуры — в первую очередь прямоугольный треугольник и квадрат. Теория к заданию №16Несмотря на то, что в задании №16 могут потребоваться любые знания по геометрии, в данном разделе мы разберем теорию по теме «окружность». Начнем рассмотрение с понятия вписанная окружность:
Хорда — длинный эластичный продольный тяж у хордовых животных; осевой скелет их предковых и некоторых современных форм. Тянется вдоль тела ниже центральной нервной системы и выше полости тела.
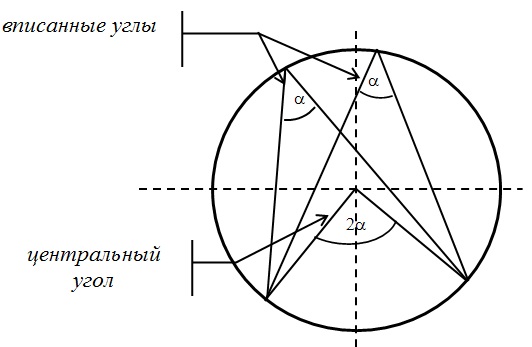
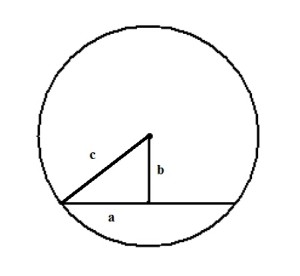
Хорда — длинный эластичный продольный тяж у хордовых животных; осевой скелет их предковых и некоторых современных форм. Тянется вдоль тела ниже центральной нервной системы и выше полости тела. Центральный и вписанный углы: Ниже я разобрал три различных примера 10 задания. Если у вас остались пожелания, или вы хотите разобрать задачу, которой здесь нет, напишите об этом в комментарии. Внимательно посмотрим на рисунок. Угол ABC опирается на дугу ADC, а угол CAD — на дугу DC. Угол, который нам необходимо найти — ABD, опирается на дугу AD — которая является частью дуги ADC за вычетом дуги DC. Значит, угол ABD равен разности углов ABC и CAD: ∠ABD = 92 — 60 = 32 pазбирался: Даниил Романович | обсудить разбор | оценить Во-первых, касательные равны между собой по длине, а значит треугольник с основанием AB равнобедренный. Угол при вершине этого треугольника равен 2 градуса по условию, значит углы при основании равны: Во-вторых, касательные перпендикулярны радиусу, то есть угол между ними и радиусом равен 90 градусов. Заметим, что угол ABO, который необходимо найти, является частью угла между касательной и радиусом, а именно за вычетом угла, который мы нашли в первом пункте. Значит, этот угол равен: pазбирался: Даниил Романович | обсудить разбор | оценить Для решения необходимо вспомнить, что центр описанной около прямоугольного треугольника окружности расположен в середине гипотенузы. То есть гипотенуза является диаметром, а её половина — радиусом. По теореме Пифагора найдем гипотенузу AB: AB² = BC² + AC² = 12² + 16² = 144 + 256 = 400 Гипотенуза равна 20, значит радиус — 10. pазбирался: Даниил Романович | обсудить разбор | оценить Для решения данной задачи необходимо провести радиус окружности к точке начала хорды: Получаем прямоугольный треугольник, где гипотенуза c — радиус и равна 13 см, b — расстояние до хорды — 5 см. По теореме Пифагора находим катет a: a² + b² = c² a² = c² — b² = 13² — 5² = 169 — 25 = 144 Откуда а = √144 = 12 Но а — лишь половина хорды, поэтому вся Хорда — длинный эластичный продольный тяж у хордовых животных; осевой скелет их предковых и некоторых современных форм. Тянется вдоль тела ниже центральной нервной системы и выше полости тела. pазбирался: Даниил Романович | обсудить разбор | оценить Сторона АВ треуг-ка АСВ является диаметром окружности. Это означает, что угол АСВ опирается на диаметр. Тогда угол АСВ равен 90 0 , и, следовательно, ∆АСВ прямоугольный. Если ∆АСВ прямоугольный, то для нахождения одной из его сторон можно применить т.Пифагора. По т.Пифагора АС 2 +ВС 2 =АВ 2 (1) По условию АС=16, радиус окружности R=10. Если R=10, то АВ=2R=2·10=20. Тогда из (1) получим: pазбирался: Даниил Романович | обсудить разбор | оценить Поскольку вершина О угла АОВ лежит в центре окружности, значит, этот угол центральный. А если так, то он равен величине дуги АВ. Т.е. ᴗАВ=113 0 . Угол АСВ является вписанным. Следовательно, его величина равна половине дуги, на которую он опирается. Из рисунка видно, что оба угла (АОВ и АСВ) опираются на одну и ту же дугу. Т.к. ᴗАВ=113 0 , то угол АСВ равен 0,5 · ᴗАВ = 0,5 · 113 0 = 56,5 0 . pазбирался: Даниил Романович | обсудить разбор | оценить Радиус вписанной в квадрат окружности равен 22 √ 2 . Найти диагональ этого квадрата. Для начала надо сделать построения на чертеже, чтобы увидеть, как располагаются известные и неизвестные элементы и чем они еще могут являться на чертеже. Обозначим диагональ АВ, точкой О – центр окружности, С – один из углов квадрата. Покажем расстояние от центра окружности до стороны квадрата – радиус r. Если радиус равен 22 √ 2 , то сторона квадрата будет в два раза больше, т.е. 44 √ 2 . Рассмотрим прямоугольный треугольник АВС, который является равнобедренным (так как по условию дан квадрат) и боковые стороны равны по 44 √ 2 . Нам надо найти диагональ, т.е. гипотенузу данного треугольника. Вспомним, что для нахождения гипотенузы равнобедренного треугольника есть формула с=а √ 2 , где с – гипотенуза, а – катет. Подставим в неё наши данные: с=44 √ 2 × √ 2 =44 √ 4 =44 × 2=88 pазбирался: Даниил Романович | обсудить разбор | оценить 🔥 ВидеоОГЭ 2023. РАЗБОР ЗАДАНИЯ №16 "Окружность"Скачать  Задание 16 ОГЭ математика 2024Скачать  ОГЭ за одну минуту | ОГЭ, математика, задание 16 (окружность и касательная)Скачать  Как решать задания на окружность ОГЭ 2021? / Разбор всех видов окружностей на ОГЭ по математикеСкачать  ОГЭ по математике 2024 геометрия | Разбор всех 16 заданийСкачать  16 задание ОГЭ математика 2023 | УмскулСкачать  ОГЭ 10 минут на подготовку. Задание 16. Четырехугольники и окружность.Скачать  ОГЭ 2022. Задания № 15, 16, 17. Часть 1 | Математика | TutorOnlineСкачать  Задание 16 (часть 1) | ОГЭ 2024 Математика | Окружность, круг и их элементыСкачать  Задача на окружности из ОГЭ-2023!! Разбор за 30 секСкачать  16 задание ОГЭ по математикеСкачать  Окружность №16 из ОГЭ. Вписанные и описанные многоугольники. Квадрат и окружность.Скачать  16 задание ОГЭ по математикеСкачать  Разбор 16 и 23 задание ОГЭ по математике 2023 | УмскулСкачать  Математика ОГЭ - 16 задание за 1 минутуСкачать 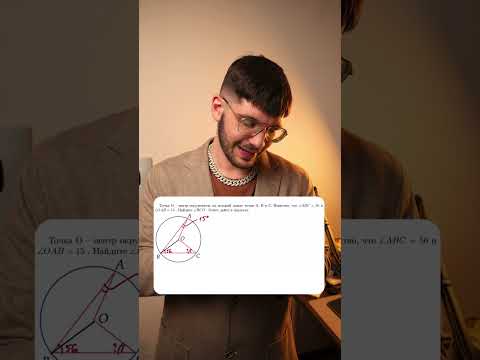 Задание 16 ОГЭ по математике. Окружность вписана в равносторонний треугольник.Скачать  Задание 16 из ОГЭ. Найдите длину большей дуги.Скачать  Задание № 16. ОГЭ - 2021. ОКРУЖНОСТЬСкачать  |
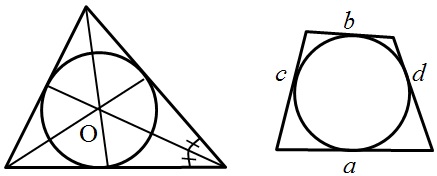 Длинна окружности и площадь:
Длинна окружности и площадь: 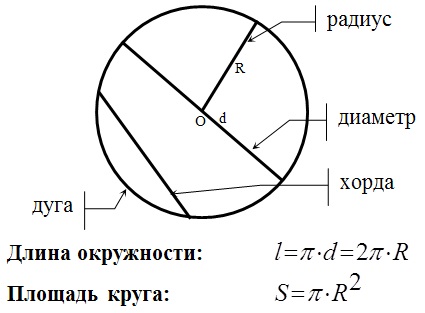 Касательная и секущая:
Касательная и секущая: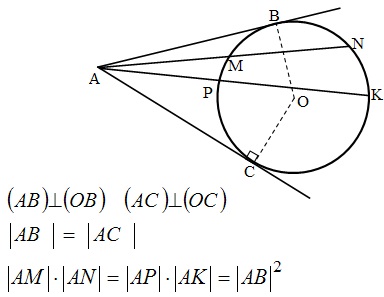 Описанная окружность и её свойства:
Описанная окружность и её свойства: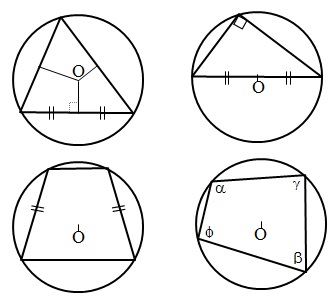
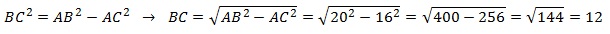 Ответ: 12
Ответ: 12
